Modeling Radar Rainfall Estimation Uncertainties: Random Error Model A
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

029I-HMVCX1924XXX-0000A0.Pdf
This Catalogue contains all Double-Sided Celebrity Records issued up to and including March 31st, 1924. The Single-Sided Celebrity Records are also included, and will be found under the records of the following artists :-CLARA Burr (all records), CARUSO and MELBA (Duet 054129), CARUSO,TETRAZZINI, AMATO, JOURNET, BADA, JACOBY (Sextet 2-054034), KUBELIK, one record only (3-7966), and TETRAZZINI, one record only (2-033027). International Celebrity Artists ALDA CORSI, A. P. GALLI-CURCI KURZ RUMFORD AMATO CORTOT GALVANY LUNN SAMMARCO ANSSEAU CULP GARRISON MARSH SCHIPA BAKLANOFF DALMORES GIGLI MARTINELLI SCHUMANN-HEINK BARTOLOMASI DE GOGORZA GILLY MCCORMACK Scorn BATTISTINI DE LUCA GLUCK MELBA SEMBRICH BONINSEGNA DE' MURO HEIFETZ MOSCISCA SMIRN6FF BORI DESTINN HEMPEL PADEREWSKI TAMAGNO BRASLAU DRAGONI HISLOP PAOLI TETRAZZINI BI1TT EAMES HOMER PARETO THIBAUD CALVE EDVINA HUGUET PATTt WERRENRATH CARUSO ELMAN JADLOWKER PLANCON WHITEHILL CASAZZA FARRAR JERITZA POLI-RANDACIO WILLIAMS CHALIAPINE FLETA JOHNSON POWELL ZANELLIi CHEMET FLONZALEY JOURNET RACHM.4NINOFF ZIMBALIST CICADA QUARTET KNIIPFER REIMERSROSINGRUFFO CLEMENT FRANZ KREISLER CORSI, E. GADSKI KUBELIK PRICES DOUBLE-SIDED RECORDS. LabelRed Price6!-867'-10-11.,613,616/- (D.A.) 10-inch - - Red (D.B.) 12-inch - - Buff (D.J.) 10-inch - - Buff (D.K.) 12-inch - - Pale Green (D.M.) 12-inch Pale Blue (D.O.) 12-inch White (D.Q.) 12-inch - SINGLE-SIDED RECORDS included in this Catalogue. Red Label 10-inch - - 5'676 12-inch - - Pale Green 12-inch - 10612,615j'- Dark Blue (C. Butt) 12-inch White (Sextet) 12-inch - ALDA, FRANCES, Soprano (Ahl'-dah) New Zealand. She Madame Frances Aida was born at Christchurch, was trained under Opera Comique Paris, Since Marcltesi, and made her debut at the in 1904. -

Amherstburg Echo Death Notices 1900
INDEX AMHERSTBURG ECHO DEATH NOTICES 1900 ----- 1909 To obtain the full announcement from the newspaper, please contact the EssexOGS Researcher at [email protected]. OR In writing to Research Coordinator, Essex County OGS, PO Box 2, Station A, Windsor, Ontario N9A 5P6 TI-IE ESSEX CO. BRANCH OF THE ONTARIO GENEALOGICAL SOCIETY 2006 The issues of this weekly newspaper are available on microfilm at the Windsor Public Library. Issues missing: 1900 - Aug. 10, 17,24, 31 - Sept. 7 1908 - Dec. 18 The issue of the newspaper may contain a more lengthy entry of the marriage or death. Births noted in this 10 year span have been indexed separately. See "Amherstburg Echo Index to Births 1900-1939" Taken from work compiled by Margaret Lane (1935-1998) ESSEX CO. BRANCI-I OF THE ONTARIO GENEALOGICAL SOCIETY AMHERSTBURG ECHO DEATHS 1900 to 1909 NAME AGE PARENT or RELATIVE DATE A Abbott, Eli Mrs. Ju1211900 Abel, David H. 69 Jan 10 1908 Abel, John H. Mrs. Aug 08 1902 Ackley, Samuel Jr. 28 Dec 02 1904 Ackley, Samuel S. 75 Dec 02 1904 Adam, A. see Adam, Paul Jun 081906 Adam, Albert see Adam, Paul Jun 08 1906 Adam, James Dr. see Adam, Paul Jun 08 1906 Adam, Lucile 06 dlo Charles Adam Nov 301900 Adam,Paul 39 slo late Matthew Adam Jun 081906 Adam, Ulric, Albert, A. see Adam, Paul Jun 08 1906 Adams, George H. see Hackett, Abba J. Feb 23 1900 Adams, George 76 Nov 061908 Adams, Henry 07 slo T.B. Adams Sep 241909 Adams, Jason 50 Sep 01 1905 Adams, Jessie (Mrs Joseph) see Fox, Adam Sep 03 1909 Adams, Joshua Mrs. -

Amherstb-Urg Echo Index O F Births, Marriages, Burials
AMHERSTB-URG ECHO INDEX O F BIRTHS, MARRIAGES, BURIALS 1940-1949 To obtain the full announcement from the newspaper, please contact the EssexOGS Researcher at [email protected]. OR In writing to Research Coordinator, Essex County OGS, PO Box 2, Station A, Windsor, Ontario N9A 5P6 ESSEX COUNTY BRANCH-ONTARIOGENEALOGICAL SOCIETY 2003 CONTENTS BIRTHS: p. 1-114 MARRIAGES: p. 1 - 65 BURIALS: p. 1 - 84 This publication was ajoint project of the l-IARROW EARLY IMMIGRANT RESEARCH SOCIETY & THE ESSEX COUNTY BRANCH, ONTARIO GENEALOGICAL SOCIETY. Transcribed & typed by Janet Ferguson Proofed & prepared for publication by J. Douglas Ouellette 2003 BIRTHS p. 1 - 114 PARENTS NAME SEX REMARKS DATE of ISSUE A Abbott, Hugh son Dennis Hugh Abbott - died Sep 91944Sep 141944 Abbott, Eugene & Betty dau Aug 5&12 1948 Abbott, Hugh son Ronald Norman Abbott Nov 241949 Abbott, Sydney son Sydney Wayne Abbott Aug 4,111949 Abbott, Michael dau Ju1261940 Abildgrad, Vernor, & Lillian dau stillborn May 10 1945 Adam, Corrine see Berns~ Howard Dec 071944 Adam, Bruno & Lena dau May 081947 Adam, Lottie see Beneteau, Norman Mar 061947 Adams, Harry son Jan 171941 Adams, Ralph & Freda son Ralph William Cutting Adams Apr 26 1940 Adams, Vincent dau Jan 311941 Adams, W.H. & Grace dan Aug 131942 Adams, Glen dau JuI051940 Adams, Harry dau Dec 161943 Adams, W.H. & Grace E. son Mar 091944 Adams, Jack & Dorothy daus twins - one infant was stillborn Oct 26 1944 Adams, Pearl see McLean,Roy Nov 131947 Adams, John son Ronald Bruce Adams Dec 091948 Adams, Harry A.R. & Mildred son Jun 171948 Adams, Stanley & Theresa son Thomas Richard Adams May 131948 Adams, Jad" dau Oct 271949 Adrian, Edna see McOuat, J.H. -

Karaoke Mietsystem Songlist
Karaoke Mietsystem Songlist Ein Karaokesystem der Firma Showtronic Solutions AG in Zusammenarbeit mit Karafun. Karaoke-Katalog Update vom: 13/10/2020 Singen Sie online auf www.karafun.de Gesamter Katalog TOP 50 Shallow - A Star is Born Take Me Home, Country Roads - John Denver Skandal im Sperrbezirk - Spider Murphy Gang Griechischer Wein - Udo Jürgens Verdammt, Ich Lieb' Dich - Matthias Reim Dancing Queen - ABBA Dance Monkey - Tones and I Breaking Free - High School Musical In The Ghetto - Elvis Presley Angels - Robbie Williams Hulapalu - Andreas Gabalier Someone Like You - Adele 99 Luftballons - Nena Tage wie diese - Die Toten Hosen Ring of Fire - Johnny Cash Lemon Tree - Fool's Garden Ohne Dich (schlaf' ich heut' nacht nicht ein) - You Are the Reason - Calum Scott Perfect - Ed Sheeran Münchener Freiheit Stand by Me - Ben E. King Im Wagen Vor Mir - Henry Valentino And Uschi Let It Go - Idina Menzel Can You Feel The Love Tonight - The Lion King Atemlos durch die Nacht - Helene Fischer Roller - Apache 207 Someone You Loved - Lewis Capaldi I Want It That Way - Backstreet Boys Über Sieben Brücken Musst Du Gehn - Peter Maffay Summer Of '69 - Bryan Adams Cordula grün - Die Draufgänger Tequila - The Champs ...Baby One More Time - Britney Spears All of Me - John Legend Barbie Girl - Aqua Chasing Cars - Snow Patrol My Way - Frank Sinatra Hallelujah - Alexandra Burke Aber Bitte Mit Sahne - Udo Jürgens Bohemian Rhapsody - Queen Wannabe - Spice Girls Schrei nach Liebe - Die Ärzte Can't Help Falling In Love - Elvis Presley Country Roads - Hermes House Band Westerland - Die Ärzte Warum hast du nicht nein gesagt - Roland Kaiser Ich war noch niemals in New York - Ich War Noch Marmor, Stein Und Eisen Bricht - Drafi Deutscher Zombie - The Cranberries Niemals In New York Ich wollte nie erwachsen sein (Nessajas Lied) - Don't Stop Believing - Journey EXPLICIT Kann Texte enthalten, die nicht für Kinder und Jugendliche geeignet sind. -
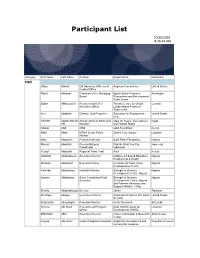
Participant List
Participant List 10/20/2019 8:45:44 AM Category First Name Last Name Position Organization Nationality CSO Jillian Abballe UN Advocacy Officer and Anglican Communion United States Head of Office Ramil Abbasov Chariman of the Managing Spektr Socio-Economic Azerbaijan Board Researches and Development Public Union Babak Abbaszadeh President and Chief Toronto Centre for Global Canada Executive Officer Leadership in Financial Supervision Amr Abdallah Director, Gulf Programs Educaiton for Employment - United States EFE HAGAR ABDELRAHM African affairs & SDGs Unit Maat for Peace, Development Egypt AN Manager and Human Rights Abukar Abdi CEO Juba Foundation Kenya Nabil Abdo MENA Senior Policy Oxfam International Lebanon Advisor Mala Abdulaziz Executive director Swift Relief Foundation Nigeria Maryati Abdullah Director/National Publish What You Pay Indonesia Coordinator Indonesia Yussuf Abdullahi Regional Team Lead Pact Kenya Abdulahi Abdulraheem Executive Director Initiative for Sound Education Nigeria Relationship & Health Muttaqa Abdulra'uf Research Fellow International Trade Union Nigeria Confederation (ITUC) Kehinde Abdulsalam Interfaith Minister Strength in Diversity Nigeria Development Centre, Nigeria Kassim Abdulsalam Zonal Coordinator/Field Strength in Diversity Nigeria Executive Development Centre, Nigeria and Farmers Advocacy and Support Initiative in Nig Shahlo Abdunabizoda Director Jahon Tajikistan Shontaye Abegaz Executive Director International Insitute for Human United States Security Subhashini Abeysinghe Research Director Verite -

Merefleksikan Kaba Anggun Nan Tongga Melalui Koreografi “Pilihan Andami”
JURNAL EKSPRESI SENI Jurnal Ilmu Pengetahuandan Karya Seni ISSN: 1412–1662 Volume 16, Nomor2,November2014, hlm. 168-335 Terbit dua kalisetahun pada bulanJuni dan November.Pengelola Jurnal Ekspresi Seni merupakan sub- sistemLPPMPPInstitut Seni Indonesia(ISI) Padangpanjang. Penanggung Jawab Rektor ISI Padangpanjang Ketua LPPMPP ISI Padangpanjang Pengarah KepalaPusat Penerbitan ISI Padangpanjang Ketua Penyunting Dede Pramayoza TimPenyunting Elizar Sri Yanto Surherni Roza Muliati Emridawati Harisman Rajudin Penterjemah Adi Khrisna Redaktur Meria Eliza Dini Yanuarmi Thegar Risky Ermiyetti Tata Letak danDesainSampul Yoni Sudiani Web Jurnal Ilham Sugesti ______________________________________________._________________________________ Alamat Pengelola Jurnal Ekspresi Seni:LPPMPP ISI Padangpanjang Jalan Bahder JohanPadangpanjang27128, Sumatera Barat; Telepon(0752) 82077 Fax. 82803, e-mail;[email protected] Catatan.Isi/Materi jurnal adalah tanggung jawab Penulis. Diterbitkan oleh Institut Seni Indonesia Padangpanjang JURNAL EKSPRESI SENI Jurnal Ilmu Pengetahuandan Karya Seni ISSN: 1412–1662 Volume 16, Nomor2,November2014, hlm. 168-335 DAFTAR ISI PENULIS JUDUL HALAMAN Aji Windu Viatra & Seni Kerajinan Songket Kampoeng Tenun di 168- 183 Slamet Triyanto Indralaya, Palembang Nofroza Yelli Bentuk Pertunjukan Saluang Orgen 184-198 dalam Acara Baralek Kawin di Kabupaten Solok Evadila Merefleksikan Kaba Anggun Nan Tongga 199–218 Melalui Koreografi “Pilihan Andami” Nurmalinda Pertunjukan Bianggung Ditinjau di Kuala Tolam 219–238 Pelalawan: Tinjauan -

Re-Writing Malay History and Identity in Faisal Tehraniâ•Žs Novel 1515
Kunapipi Volume 32 Issue 1 Article 9 2010 The empire strikes back: Re-Writing malay history and identity in Faisal Tehrani’s novel 1515 MD. Salleh Yaapar Follow this and additional works at: https://ro.uow.edu.au/kunapipi Part of the Arts and Humanities Commons Recommended Citation Yaapar, MD. Salleh, The empire strikes back: Re-Writing malay history and identity in Faisal Tehrani’s novel 1515, Kunapipi, 32(1), 2010. Available at:https://ro.uow.edu.au/kunapipi/vol32/iss1/9 Research Online is the open access institutional repository for the University of Wollongong. For further information contact the UOW Library: [email protected] The empire strikes back: Re-Writing malay history and identity in Faisal Tehrani’s novel 1515 Abstract Published in 2003, 1515 by Faisal Tehrani is a unique text within contemporary Malay literature. Among recent novels in Malaysia it is one of the most difficulteadings, r but probably the most refreshing and rewarding one. Perhaps it is also one of the most multifaceted narratives, with elements of romance, adventure, history, legend, postcolonial discourse, postmodernism, socio-political criticism, feminism, and even fantasy. Consequently, the novel also lends itself to various ways of reading: from the perspective of postcolonial, postmodern, socio-political, and feminist theories, or a blending of all of them. Although the novel appears to be postmodern and unique, it in fact is connected not only to postmodernism and magic realism (as associated with Carlos Fuentes and Gabriel Garcia Marquez), but perhaps more importantly it draws on a long established tradition of Malay folk literature, specifically the folk omancer known as cerita penglipur lara (tales of soother of cares). -

Eurovision Karaoke
1 Eurovision Karaoke ALBANÍA ASERBAÍDJAN ALB 06 Zjarr e ftohtë AZE 08 Day after day ALB 07 Hear My Plea AZE 09 Always ALB 10 It's All About You AZE 14 Start The Fire ALB 12 Suus AZE 15 Hour of the Wolf ALB 13 Identitet AZE 16 Miracle ALB 14 Hersi - One Night's Anger ALB 15 I’m Alive AUSTURRÍKI ALB 16 Fairytale AUT 89 Nur ein Lied ANDORRA AUT 90 Keine Mauern mehr AUT 04 Du bist AND 07 Salvem el món AUT 07 Get a life - get alive AUT 11 The Secret Is Love ARMENÍA AUT 12 Woki Mit Deim Popo AUT 13 Shine ARM 07 Anytime you need AUT 14 Conchita Wurst- Rise Like a Phoenix ARM 08 Qele Qele AUT 15 I Am Yours ARM 09 Nor Par (Jan Jan) AUT 16 Loin d’Ici ARM 10 Apricot Stone ARM 11 Boom Boom ÁSTRALÍA ARM 13 Lonely Planet AUS 15 Tonight Again ARM 14 Aram Mp3- Not Alone AUS 16 Sound of Silence ARM 15 Face the Shadow ARM 16 LoveWave 2 Eurovision Karaoke BELGÍA UKI 10 That Sounds Good To Me UKI 11 I Can BEL 86 J'aime la vie UKI 12 Love Will Set You Free BEL 87 Soldiers of love UKI 13 Believe in Me BEL 89 Door de wind UKI 14 Molly- Children of the Universe BEL 98 Dis oui UKI 15 Still in Love with You BEL 06 Je t'adore UKI 16 You’re Not Alone BEL 12 Would You? BEL 15 Rhythm Inside BÚLGARÍA BEL 16 What’s the Pressure BUL 05 Lorraine BOSNÍA OG HERSEGÓVÍNA BUL 07 Water BUL 12 Love Unlimited BOS 99 Putnici BUL 13 Samo Shampioni BOS 06 Lejla BUL 16 If Love Was a Crime BOS 07 Rijeka bez imena BOS 08 D Pokušaj DUET VERSION DANMÖRK BOS 08 S Pokušaj BOS 11 Love In Rewind DEN 97 Stemmen i mit liv BOS 12 Korake Ti Znam DEN 00 Fly on the wings of love BOS 16 Ljubav Je DEN 06 Twist of love DEN 07 Drama queen BRETLAND DEN 10 New Tomorrow DEN 12 Should've Known Better UKI 83 I'm never giving up DEN 13 Only Teardrops UKI 96 Ooh aah.. -

Eurovision Karaoke
1 Eurovision Karaoke Eurovision Karaoke 2 Eurovision Karaoke ALBANÍA AUS 14 Conchita Wurst- Rise Like a Phoenix ALB 07 Hear My Plea BELGÍA ALB 10 It's All About You BEL 06 Je t'adore ALB 12 Suus BEL 12 Would You? ALB 13 Identitet BEL 86 J'aime la vie ALB 14 Hersi - One Night's Anger BEL 87 Soldiers of love BEL 89 Door de wind BEL 98 Dis oui ARMENÍA ARM 07 Anytime you need BOSNÍA OG HERSEGÓVÍNA ARM 08 Qele Qele BOS 99 Putnici ARM 09 Nor Par (Jan Jan) BOS 06 Lejla ARM 10 Apricot Stone BOS 07 Rijeka bez imena ARM 11 Boom Boom ARM 13 Lonely Planet ARM 14 Aram Mp3- Not Alone BOS 11 Love In Rewind BOS 12 Korake Ti Znam ASERBAÍDSJAN AZE 08 Day after day BRETLAND AZE 09 Always UKI 83 I'm never giving up AZE 14 Start The Fire UKI 96 Ooh aah... just a little bit UKI 04 Hold onto our love AUSTURRÍKI UKI 07 Flying the flag (for you) AUS 89 Nur ein Lied UKI 10 That Sounds Good To Me AUS 90 Keine Mauern mehr UKI 11 I Can AUS 04 Du bist UKI 12 Love Will Set You Free AUS 07 Get a life - get alive UKI 13 Believe in Me AUS 11 The Secret Is Love UKI 14 Molly- Children of the Universe AUS 12 Woki Mit Deim Popo AUS 13 Shine 3 Eurovision Karaoke BÚLGARÍA FIN 13 Marry Me BUL 05 Lorraine FIN 84 Hengaillaan BUL 07 Water BUL 12 Love Unlimited FRAKKLAND BUL 13 Samo Shampioni FRA 69 Un jour, un enfant DANMÖRK FRA 93 Mama Corsica DEN 97 Stemmen i mit liv DEN 00 Fly on the wings of love FRA 03 Monts et merveilles DEN 06 Twist of love DEN 07 Drama queen DEN 10 New Tomorrow FRA 09 Et S'il Fallait Le Faire DEN 12 Should've Known Better FRA 11 Sognu DEN 13 Only Teardrops -

Download Booklet
HarmoniousThe EchoSONGS BY SIR ARTHUR SULLIVAN MARY BEVAN • KITTY WHATELY soprano mezzo-soprano BEN JOHNSON • ASHLEY RICHES tenor bass-baritone DAVID OWEN NORRIS piano Sir Arthur Sullivan, Ottawa, 1880 Ottawa, Sullivan, Arthur Sir Photograph by Topley, Ottawa, Canada /Courtesy of David B. Lovell Collection Sir Arthur Sullivan (1842 – 1900) Songs COMPACT DISC ONE 1 King Henry’s Song (1877)* 2:23 (‘Youth will needs have dalliance’) with Chorus ad libitum from incidental music to Henry VIII (1613) by William Shakespeare (1564 – 1616) and John Fletcher (1579 – 1625) Andante moderato Recording sponsored by Martin Yates 3 2 The Lady of the Lake (1864)† 3:25 from Kenilworth, ‘A Masque of the Days of Queen Elizabeth’, Op. 4 (or The Masque at Kenilworth) (1864) Libretto by Henry Fothergill Chorley (1808 – 1872) Allegro grazioso 3 I heard the nightingale (1863)‡ 2:59 Dedicated to his Friend Captain C.J. Ottley Allegretto moderato 4 Over the roof (1864)† 3:04 from the opera The Sapphire Necklace, or the False Heiress Libretto by Henry Fothergill Chorley Allegretto moderato Recording sponsored by Michael Symes 4 5 Will He Come? (1865)§ 4:05 Dedicated to The Lady Katherine Coke Composed expressly for Madame Sainton Dolby Moderato e tranquillo – Quasi Recitativo – Tranquillo un poco più lento Recording sponsored by Michael Tomlinson 6 Give (1867)† 4:56 Composed and affectionately dedicated to Mrs Helmore Allegretto – Un poco più lento – Lento Recording sponsored by John Thrower in memory of Simon and Brenda Walton 7 Thou art weary (1874)§ 5:00 Allegro vivace e agitato – Più lento – Allegro. Tempo I – Più lento – Allegro. -

Download Booklet
660185-86bk Gluck US 11/01/2005 03:04pm Page 28 ORPHÉE ORPHEUS Ah, justes dieux! Ah, just gods! Quelle est notre reconnaissance! How grateful we are! GLUCK L’AMOUR LOVE Ne doutez plus de ma puissance. No longer doubt my power. Orphée et Euridice Je viens vous retirer de cet affreux séjour. I have come to take you from this dreary abode. Jouissez désormais des faveurs de l’amour. Enjoy henceforth the favour of love. (1774 Paris Version) SCÈNE III SCENE III Fouchécourt • Dubosc • Le Blanc Temple magnifique dédié à l’Amour. Orphée, Magnificent temple dedicated to Love. Orpheus, Euridice et l’Amour, précédés de bergers et de Euridice and Love, preceded by shepherds and Opera Lafayette Orchestra and Chorus nymphes qui viennent fêter le retour d’Euridice. nymphs coming to celebrate Euridice’s return. Ryan Brown ORPHÉE ORPHEUS L’Amour triomphe, Love is triumphant, Et tout ce qui respire and all living things Sert l’empire de la beauté. are servants of beauty. Sa chaîne agréable Its pleasant bonds Est préférable à la liberté. are preferable to liberty. LE CHOEUR CHORUS L’Amour triomphe, etc. Love is triumphant, etc. L’AMOUR LOVE Dans les peines, dans les alarmes In pain and in worry Je fais souvent languir les coeurs. I often cause hearts to languish. Mais, dans un instant, mes charmes But, in an instant, my magic Font pour jamais oublier mes rigueurs. causes my severity to be forgotten forever. LE CHOEUR CHORUS L’Amour triomphe, etc. Love is triumphant, etc. EURIDICE EURIDICE Si la cruelle jalousie If cruel jealousy A troublé mes tendres désirs, troubled my tender desires, Les douceurs dont elle est suivie the joys which followed it Sont des chaînes de plaisirs. -

ECHO Rappor T Annuel 1999
Office d’aide humanitaire Timor oriental: Un espoir de paix ECHO Rapport Annuel 1999 Office d’aide humanitaire Photo de couverture: camp de réfugiés d’Atenbua, Timor occidental, novembre dernier. De son abri, une famille du Timor a le regard tourné vers les envoyés des Nations Unies qui proposent le rapatriement vers le Timor oriental. Photo: DARREN WHITESIDE, Reuters ACRONYMES ECHO L’Office d’aide humanitaire UE Union européenne CICR Comité International de la Croix Rouge FICR Fédération internationale des sociétés de la Croix Rouge et du Croissant Rouge ONG Organisation non gouvernementale HCRNU Haut commissariat pour les réfugiés des Nations unies PAM Programme alimentaire mondial REMERCIEMENTS Nous remercions tous ceux qui nous ont offert les droits de reproduction de leurs photographies. Les photo- graphies des pages de couverture, des pages 4-5 et 17 nous ont été données gracieusement par la Fondation Reuters Alertnet (www.alertnet.org.). La Prière pour la Paix en Sierra Leone (page 24) nous a été transmise dans le cadre du projet de l’ONG Visual Impact ([email protected]) Editeur : Costanza Adinolfi, Directeur, ECHO Texte, coordination : ECHO Information Conception, mise en page : Makers, Bruxelles REPRODUCTION AUTORISEE, MOYENNANT MENTION DE LA SOURCE Of ‘ fice d’aidehumanitair MEMESSASSAGGEE D DUU CO COMMIMMISSAISSAIRERE La fin du millénaire nous rappelle la triste réalité : les conflits continuent à occuper le devant de la scène internationale. e année 1999 aura l’ensemble jugé positivement les efforts déployés par ECHO. ‘été marquée par Ils ont constaté qu’il remplissait son rôle aussi bien, sinon L’des événements mieux, qu’aucune autre organisation internationale majeurs au Kosovo, au comparable.