DOCSLIB.ORG

Exploring the Potential of Machine Learning Methods and Selection

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Exploring the Potential of Machine Learning Methods and Selection From the Institute of Animal Breeding and Genetics Justus-Liebig-University Gießen Exploring the potential of machine learning methods and selection signature analyses for the estimation of genomic breeding values, the estimation of SNP effects and the identification of possible candidate genes in dairy cattle Dissertation to obtain the doctoral degree (Dr. agr.) in the Faculty of Agricultural Science, Nutritional Science and Environmental Management of Justus-Liebig-University Gießen, Germany presented by Saeid Naderi Darbaghshahi born in Esfahan, Iran Gießen, March 2018 1st Referee: Prof. Dr. Sven König Institute of Animal Breeding and Genetics Justus-Liebig-University Gießen, Germany 2nd Referee: Prof. Dr. Nicolas Gengler Animal Science Unit, Numerical Genetics, Genomics and Modeling Agriculture, Bio-engineering and Chemistry Department University of Liège - Gembloux Agro-Bio Tech, Belgium Table of Contents SUMMARY ........................................................................................................................... 1 1st Chapter General introduction ........................................................................................... 3 From conventional pedigree-based selection towards genomic selection ............................. 4 Effects of genomic selection on rate of genetic gain ............................................................. 5 Factors that affect accuracy of genomic prediction ............................................................... 5 Methods of genomic prediction ............................................................................................. 7 Genomic selection for disease resistance using cow training set ........................................ 10 From genome wide association study (GWAS) to identification of selection signatures ... 10 Cross-population extended haplotype homozygosity (XP-EHH). ....................................... 12 Objectives of the thesis ........................................................................................................ 13 2nd Chapter Random forest estimation of genomic breeding values for disease susceptibility over different disease incidences and genomic architectures in simulated cow calibration groups ………………………………………………………………….......….....….....….......………......21 3rd Chapter Genomic breeding values, SNP effects and gene identification for disease traits in cow training sets …………………………………………………………..………....………….. 47 4th Chapter Assessing signatures of selection through variation in linkage disequilibrium within and between dual-purpose black and white (DSN) and German Holstein cattle populations …...………………………………………………………………………………………………............81 5th Chapter General Discussion ...................................................................................... 118 Preface and Overview ........................................................................................................ 119 Impact of disease incidences in the cow training set on accuracies of GEBV .................. 120 Impact of genetic architecture of traits on accuracies of GEBV ....................................... 121 Impact of the model choice on accuracies of GEBV ......................................................... 123 Assessing predictive ability using receiver operator characteristic (ROC) curves ............ 123 Theoretical expectations and AUCmax ............................................................................... 124 Utilization SNP correlations from random forest for genome wide association studies ... 126 Detection of selection signature ......................................................................................... 127 Signatures of positive selection revealed by FST .............................................................. 128 Holstein and DSN .............................................................................................................. 128 East-DSN and West-DSN .................................................................................................. 129 Sick and healthy Holstein cows ......................................................................................... 130 CONCLUSION .................................................................................................................. 131 LIST OF TABLES 2nd Chapter Table 1: The evaluated scenarios with respect to the no. of markers and QTL, the heritability of the trait, and the level of linkage disequilibrium (LD) .................................................................... 25 Table 2: Parameters of the simulation process .............................................................................. 27 Table 3: Correlation between true and predicted genomic breeding values for S_I (10K SNP, h2 =0.30 and 725 QTL), S_II (10K SNP, h2 =0.30 and 290 QTL) and S_III (10K SNP, h2 =0.10 and 290 QTL) from RF and GBLUP applications (the values in parenthesis show the SD from ten replicates) ........................................................................................................................................ 33 Table 4: The area under the receiving operating characteristic curve (AUROC) for S_I (10K SNP, h2 =0.30 and 725 QTL), S_II (10K SNP, h2 =0.30 and 290 QTL) and S_III (10K SNP, h2 =0.10 and 290 QTL) from RF and GBLUP applications (the values in parenthesis show the SD from ten replicates). ......................................................................................................................... 34 Table 5: Correlation between true and predicted genomic breeding values for S_IV (50K SNP, h2 =0.30 and 725 QTL), S_V (50K SNP, h2 =0.30 and 290 QTL), S_VI (50K SNP, h2 =0.10 and 290 QTL) and S_VII (50K SNP, h2 =0.10, 290 QTL and high LD) from RF and GBLUP applications (the values in parenthesis show the SD from ten replicates) .......................................................... 35 Table 6: The area under the receiving operating characteristic curve (AUROC) for S_IV (50K SNP, h2 =0.30 and 725 QTL), S_V (50K SNP, h2 =0.30 and 290 QTL), S_VI (50K SNP, h2 = 0.10 and 290 QTL) and S_VII (50K SNP, h2 = 0.10, 290 QTL and high LD) from RF and GBLUP applications (the values in parenthesis show the SD from ten replicates). ..................................... 36 Table 7: The calculated r2 between each of ten most effective QTL and the most important SNP located in the same chromosome for scenarios S_I (10K SNP chip, h2 = 0.3 and QTL = 725) and S_IV (50K SNP chip, h2 = 0.3 and QTL = 725) ............................................................................ 38 3rd Chapter Table 1: Overview of health disorders as used in the present study along with their disease incidences (in %) in the total data set (T) and in the dataset of genotyped cows (G) ................. 52 Table 2: SNP associations for laminitis, dermatitis digitalis, clinical mastitis and endometritis with false discovery rate (FDR) ≤ 10% from GWAS, the most important variable from RF (VIM = 1) and annotated genes in 500 Kb up and downstream of the given SNP ................................... 68 4th Chapter Table 1: The regions under positive selection in the DSN population and the annotated potential candidate genes within a window of 250 Kb downstream and upstream of each core SNP .......... 92 Table 2: The regions under positive selection in the Holstein population and the annotated genes in a window of 250 Kb downstream and upstream of each core SNP ........................................... 94 Table 3: The regions under positive selection in the East-DSN sub-population and the annotated genes in a window of 250 Kb downstream and upstream of each core SNP .................................. 97 Table 4: The regions under positive selection in West-DSN sub-population and the annotated genes in a window of 250 Kb downstream and upstream of each core SNP ................................ 100 Table 5: The regions under positive selection in the healthy Holstein sub-population and the annotated genes in a window of 250 Kb downstream and upstream of each core SNP ............... 103 Table 6: The regions under positive selection in the sick Holstein sub-population and the annotated genes in a window of 250 Kb downstream and upstream of each core SNP ............... 107 LIST OF FIGURES 2nd Chapter Figure 1: Strategy for the creation of training and testing sets ...................................................... 30 Figure 2: The relative importance of each 10K (a) and 50K (b) SNP, and positions and percentage of phenotypic variance related to ten top QTL (black circles) along 29 chromosomes ......................................................................................................................................................... 42 3rd Chapter Figure 1: Correlation between de-regressed proofs and genomic breeding values (rGBV) and the corrected prediction accuracy using the ―Wellmann-equation‖ (rGBV-cor) for claw disorders (A), for clinical mastitis (B) and for infertility (C) from random forest (RF) and genomic BLUP (GBLUP) applications ...................................................................................................................................... 60 Figure 2: Prediction accuracy (rGBV-PCP) for claw disorders (A), for clinical mastitis (B) and for infertility (C) from random forest (RF), genomic BLUP (GBLUP) and single step genomic BLUP (ssGBLUP) applications .................................................................................................................
Load more

Recommended publications
  • The Significance of the Evolutionary Relationship of Prion Proteins and ZIP Transporters in Health and Disease
    The Significance of the Evolutionary Relationship of Prion Proteins and ZIP Transporters in Health and Disease by Sepehr Ehsani A thesis submitted in conformity with the requirements for the degree of Doctor of Philosophy Department of Laboratory Medicine and Pathobiology University of Toronto © Copyright by Sepehr Ehsani 2012 The Significance of the Evolutionary Relationship of Prion Proteins and ZIP Transporters in Health and Disease Sepehr Ehsani Doctor of Philosophy Department of Laboratory Medicine and Pathobiology University of Toronto 2012 Abstract The cellular prion protein (PrPC) is unique amongst mammalian proteins in that it not only has the capacity to aggregate (in the form of scrapie PrP; PrPSc) and cause neuronal degeneration, but can also act as an independent vector for the transmission of disease from one individual to another of the same or, in some instances, other species. Since the discovery of PrPC nearly thirty years ago, two salient questions have remained largely unanswered, namely, (i) what is the normal function of the cellular protein in the central nervous system, and (ii) what is/are the factor(s) involved in the misfolding of PrPC into PrPSc? To shed light on aspects of these questions, we undertook a discovery-based interactome investigation of PrPC in mouse neuroblastoma cells (Chapter 2), and among the candidate interactors, identified two members of the ZIP family of zinc transporters (ZIP6 and ZIP10) as possessing a PrP-like domain. Detailed analyses revealed that the LIV-1 subfamily of ZIP transporters (to which ZIPs 6 and 10 belong) are in fact the evolutionary ancestors of prions (Chapter 3).
    [Show full text]
  • Genome-Wide Analysis of Allele-Specific Expression Patterns in Seventeen Tissues of Korean Cattle (Hanwoo)
    animals Article Genome-Wide Analysis of Allele-Specific Expression Patterns in Seventeen Tissues of Korean Cattle (Hanwoo) Kyu-Sang Lim 1 , Sun-Sik Chang 2, Bong-Hwan Choi 3, Seung-Hwan Lee 4, Kyung-Tai Lee 3 , Han-Ha Chai 3, Jong-Eun Park 3 , Woncheoul Park 3 and Dajeong Lim 3,* 1 Department of Animal Science, Iowa State University, Ames, IA 50011, USA; [email protected] 2 Hanwoo Research Institute, National Institute of Animal Science, Rural Development Administration, Pyeongchang 25340, Korea; [email protected] 3 Animal Genomics and Bioinformatics Division, National Institute of Animal Science, Rural Development Administration, Wanju 55365, Korea; [email protected] (B.-H.C.); [email protected] (K.-T.L.); [email protected] (H.-H.C.); [email protected] (J.-E.P.); [email protected] (W.P.) 4 Division of Animal and Dairy Science, Chungnam National University, Daejeon 34134, Korea; [email protected] * Correspondence: [email protected] Received: 26 July 2019; Accepted: 23 September 2019; Published: 26 September 2019 Simple Summary: Allele-specific expression (ASE) is the biased allelic expression of genetic variants within the gene. Recently, the next-generation sequencing (NGS) technologies allowed us to detect ASE genes at a transcriptome-wide level. It is essential for the understanding of animal development, cellular programming, and the effect on their complexity because ASE shows developmental, tissue, or species-specific patterns. However, these aspects of ASE still have not been annotated well in farm animals and most studies were conducted mainly at the fetal stages. Hence, the current study focuses on detecting ASE genes in 17 tissues in adult cattle.
    [Show full text]
  • Function and Gene Expression of Circulating Neutrophils in Dairy Cows: Impact of Micronutrient Supplementation
    FUNCTION AND GENE EXPRESSION OF CIRCULATING NEUTROPHILS IN DAIRY COWS: IMPACT OF MICRONUTRIENT SUPPLEMENTATION A Dissertation Presented to The Faculty of the Graduate School At The University of Missouri In Partial Fulfillment Of the Requirements for the Degree Doctor of Philosophy By Xavier S. Revelo Dr. Matthew R. Waldron, Dissertation Supervisor July, 2012 ©Copyright by Xavier S. Revelo 2012 All rights reserved The undersigned, appointed by the dean of the Graduate School, have examined the dissertation entitled: FUNCTION AND GENE EXPRESSION OF CIRCULATING NEUTROPHILS IN DAIRY COWS: IMPACT OF MICRONUTRIENT SUPPLEMENTATION Presented by Xavier Revelo A candidate for the degree of Doctor of Philosophy in Animal Sciences And hereby certify that, in their opinion, it is worthy of acceptance. Dissertation Examination Committee: ________________________ Advisor Matthew R. Waldron, Ph.D. ________________________ Kevin L. Fritsche, Ph.D. ________________________ Matthew C. Lucy, Ph.D. ________________________ James W. Perfield, Ph.D. ACKNOWLEDGEMENTS First of all, I would like to thank my family for their patience, love and inseparable support even after all the years that I have been away from home. Thanks to my mother Sonia for dedicating her life to the guidance, inspiration, and nurturance of our family. I have been blessed with a loving and devoted family who gave me the motivation I needed to pursue my professional goals. I would also like to offer my sincerest gratitude to the friends I made while pursuing my doctorate degree at the University of Missouri. Special thanks to Daniel Mathew, Brad Scharf, Ky Pohler, Eric Coate, and Emma Jinks for sharing their time and friendship.
    [Show full text]
  • A Computational Approach for Defining a Signature of Β-Cell Golgi Stress in Diabetes Mellitus
    Page 1 of 781 Diabetes A Computational Approach for Defining a Signature of β-Cell Golgi Stress in Diabetes Mellitus Robert N. Bone1,6,7, Olufunmilola Oyebamiji2, Sayali Talware2, Sharmila Selvaraj2, Preethi Krishnan3,6, Farooq Syed1,6,7, Huanmei Wu2, Carmella Evans-Molina 1,3,4,5,6,7,8* Departments of 1Pediatrics, 3Medicine, 4Anatomy, Cell Biology & Physiology, 5Biochemistry & Molecular Biology, the 6Center for Diabetes & Metabolic Diseases, and the 7Herman B. Wells Center for Pediatric Research, Indiana University School of Medicine, Indianapolis, IN 46202; 2Department of BioHealth Informatics, Indiana University-Purdue University Indianapolis, Indianapolis, IN, 46202; 8Roudebush VA Medical Center, Indianapolis, IN 46202. *Corresponding Author(s): Carmella Evans-Molina, MD, PhD ([email protected]) Indiana University School of Medicine, 635 Barnhill Drive, MS 2031A, Indianapolis, IN 46202, Telephone: (317) 274-4145, Fax (317) 274-4107 Running Title: Golgi Stress Response in Diabetes Word Count: 4358 Number of Figures: 6 Keywords: Golgi apparatus stress, Islets, β cell, Type 1 diabetes, Type 2 diabetes 1 Diabetes Publish Ahead of Print, published online August 20, 2020 Diabetes Page 2 of 781 ABSTRACT The Golgi apparatus (GA) is an important site of insulin processing and granule maturation, but whether GA organelle dysfunction and GA stress are present in the diabetic β-cell has not been tested. We utilized an informatics-based approach to develop a transcriptional signature of β-cell GA stress using existing RNA sequencing and microarray datasets generated using human islets from donors with diabetes and islets where type 1(T1D) and type 2 diabetes (T2D) had been modeled ex vivo. To narrow our results to GA-specific genes, we applied a filter set of 1,030 genes accepted as GA associated.
    [Show full text]
  • Screening of a Clinically and Biochemically Diagnosed SOD Patient Using Exome Sequencing: a Case Report with a Mutations/Variations Analysis Approach
    The Egyptian Journal of Medical Human Genetics (2016) 17, 131–136 HOSTED BY Ain Shams University The Egyptian Journal of Medical Human Genetics www.ejmhg.eg.net www.sciencedirect.com CASE REPORT Screening of a clinically and biochemically diagnosed SOD patient using exome sequencing: A case report with a mutations/variations analysis approach Mohamad-Reza Aghanoori a,b,1, Ghazaleh Mohammadzadeh Shahriary c,2, Mahdi Safarpour d,3, Ahmad Ebrahimi d,* a Department of Medical Genetics, Shiraz University of Medical Sciences, Shiraz, Iran b Research and Development Division, RoyaBioGene Co., Tehran, Iran c Department of Genetics, Shahid Chamran University of Ahvaz, Ahvaz, Iran d Cellular and Molecular Research Center, Research Institute for Endocrine Sciences, Shahid Beheshti University of Medical Sciences, Tehran, Iran Received 12 May 2015; accepted 15 June 2015 Available online 22 July 2015 KEYWORDS Abstract Background: Sulfite oxidase deficiency (SOD) is a rare neurometabolic inherited disor- Sulfite oxidase deficiency; der causing severe delay in developmental stages and premature death. The disease follows an auto- Case report; somal recessive pattern of inheritance and causes deficiency in the activity of sulfite oxidase, an Exome sequencing enzyme that normally catalyzes conversion of sulfite to sulfate. Aim of the study: SOD is an underdiagnosed disorder and its diagnosis can be difficult in young infants as early clinical features and neuroimaging changes may imitate some common diseases. Since the prognosis of the disease is poor, using exome sequencing as a powerful and efficient strat- egy for identifying the genes underlying rare mendelian disorders can provide important knowledge about early diagnosis, disease mechanisms, biological pathways, and potential therapeutic targets.
    [Show full text]
  • Tepzz¥ 6Z54za T
    (19) TZZ¥ ZZ_T (11) EP 3 260 540 A1 (12) EUROPEAN PATENT APPLICATION (43) Date of publication: (51) Int Cl.: 27.12.2017 Bulletin 2017/52 C12N 15/113 (2010.01) A61K 9/127 (2006.01) A61K 31/713 (2006.01) C12Q 1/68 (2006.01) (21) Application number: 17000579.7 (22) Date of filing: 12.11.2011 (84) Designated Contracting States: • Sarma, Kavitha AL AT BE BG CH CY CZ DE DK EE ES FI FR GB Philadelphia, PA 19146 (US) GR HR HU IE IS IT LI LT LU LV MC MK MT NL NO • Borowsky, Mark PL PT RO RS SE SI SK SM TR Needham, MA 02494 (US) • Ohsumi, Toshiro Kendrick (30) Priority: 12.11.2010 US 412862 P Cambridge, MA 02141 (US) 20.12.2010 US 201061425174 P 28.07.2011 US 201161512754 P (74) Representative: Clegg, Richard Ian et al Mewburn Ellis LLP (62) Document number(s) of the earlier application(s) in City Tower accordance with Art. 76 EPC: 40 Basinghall Street 11840099.3 / 2 638 163 London EC2V 5DE (GB) (71) Applicant: The General Hospital Corporation Remarks: Boston, MA 02114 (US) •Thecomplete document including Reference Tables and the Sequence Listing can be downloaded from (72) Inventors: the EPO website • Lee, Jeannie T •This application was filed on 05-04-2017 as a Boston, MA 02114 (US) divisional application to the application mentioned • Zhao, Jing under INID code 62. San Diego, CA 92122 (US) •Claims filed after the date of receipt of the divisional application (Rule 68(4) EPC). (54) POLYCOMB-ASSOCIATED NON-CODING RNAS (57) This invention relates to long non-coding RNAs (IncRNAs), libraries of those ncRNAs that bind chromatin modifiers, such as Polycomb Repressive Complex 2, inhibitory nucleic acids and methods and compositions for targeting IncRNAs.
    [Show full text]
  • An Integrative, Genomic, Transcriptomic and Network-Assisted
    Yan et al. BMC Medical Genomics 2020, 13(Suppl 5):39 https://doi.org/10.1186/s12920-020-0675-4 RESEARCH Open Access An integrative, genomic, transcriptomic and network-assisted study to identify genes associated with human cleft lip with or without cleft palate Fangfang Yan1†, Yulin Dai1†, Junichi Iwata2,3, Zhongming Zhao1,4,5* and Peilin Jia1* From The International Conference on Intelligent Biology and Medicine (ICIBM) 2019 Columbus, OH, USA. 9-11 June 2019 Abstract Background: Cleft lip with or without cleft palate (CL/P) is one of the most common congenital human birth defects. A combination of genetic and epidemiology studies has contributed to a better knowledge of CL/P-associated candidate genes and environmental risk factors. However, the etiology of CL/P remains not fully understood. In this study, to identify new CL/P-associated genes, we conducted an integrative analysis using our in-house network tools, dmGWAS [dense module search for Genome-Wide Association Studies (GWAS)] and EW_dmGWAS (Edge-Weighted dmGWAS), in a combination with GWAS data, the human protein-protein interaction (PPI) network, and differential gene expression profiles. Results: A total of 87 genes were consistently detected in both European and Asian ancestries in dmGWAS. There were 31.0% (27/87) showed nominal significance with CL/P (gene-based p < 0.05), with three genes showing strong association signals, including KIAA1598, GPR183,andZMYND11 (p <1×10− 3). In EW_dmGWAS, we identified 253 and 245 module genes associated with CL/P for European ancestry and the Asian ancestry, respectively. Functional enrichment analysis demonstrated that these genes were involved in cell adhesion, protein localization to the plasma membrane, the regulation of the apoptotic signaling pathway, and other pathological conditions.
    [Show full text]
  • Supplementary Table S4. FGA Co-Expressed Gene List in LUAD
    Supplementary Table S4. FGA co-expressed gene list in LUAD tumors Symbol R Locus Description FGG 0.919 4q28 fibrinogen gamma chain FGL1 0.635 8p22 fibrinogen-like 1 SLC7A2 0.536 8p22 solute carrier family 7 (cationic amino acid transporter, y+ system), member 2 DUSP4 0.521 8p12-p11 dual specificity phosphatase 4 HAL 0.51 12q22-q24.1histidine ammonia-lyase PDE4D 0.499 5q12 phosphodiesterase 4D, cAMP-specific FURIN 0.497 15q26.1 furin (paired basic amino acid cleaving enzyme) CPS1 0.49 2q35 carbamoyl-phosphate synthase 1, mitochondrial TESC 0.478 12q24.22 tescalcin INHA 0.465 2q35 inhibin, alpha S100P 0.461 4p16 S100 calcium binding protein P VPS37A 0.447 8p22 vacuolar protein sorting 37 homolog A (S. cerevisiae) SLC16A14 0.447 2q36.3 solute carrier family 16, member 14 PPARGC1A 0.443 4p15.1 peroxisome proliferator-activated receptor gamma, coactivator 1 alpha SIK1 0.435 21q22.3 salt-inducible kinase 1 IRS2 0.434 13q34 insulin receptor substrate 2 RND1 0.433 12q12 Rho family GTPase 1 HGD 0.433 3q13.33 homogentisate 1,2-dioxygenase PTP4A1 0.432 6q12 protein tyrosine phosphatase type IVA, member 1 C8orf4 0.428 8p11.2 chromosome 8 open reading frame 4 DDC 0.427 7p12.2 dopa decarboxylase (aromatic L-amino acid decarboxylase) TACC2 0.427 10q26 transforming, acidic coiled-coil containing protein 2 MUC13 0.422 3q21.2 mucin 13, cell surface associated C5 0.412 9q33-q34 complement component 5 NR4A2 0.412 2q22-q23 nuclear receptor subfamily 4, group A, member 2 EYS 0.411 6q12 eyes shut homolog (Drosophila) GPX2 0.406 14q24.1 glutathione peroxidase
    [Show full text]
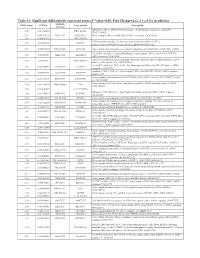
  • (P -Value<0.05, Fold Change≥1.4), 4 Vs. 0 Gy Irradiation
    Table S1: Significant differentially expressed genes (P -Value<0.05, Fold Change≥1.4), 4 vs. 0 Gy irradiation Genbank Fold Change P -Value Gene Symbol Description Accession Q9F8M7_CARHY (Q9F8M7) DTDP-glucose 4,6-dehydratase (Fragment), partial (9%) 6.70 0.017399678 THC2699065 [THC2719287] 5.53 0.003379195 BC013657 BC013657 Homo sapiens cDNA clone IMAGE:4152983, partial cds. [BC013657] 5.10 0.024641735 THC2750781 Ciliary dynein heavy chain 5 (Axonemal beta dynein heavy chain 5) (HL1). 4.07 0.04353262 DNAH5 [Source:Uniprot/SWISSPROT;Acc:Q8TE73] [ENST00000382416] 3.81 0.002855909 NM_145263 SPATA18 Homo sapiens spermatogenesis associated 18 homolog (rat) (SPATA18), mRNA [NM_145263] AA418814 zw01a02.s1 Soares_NhHMPu_S1 Homo sapiens cDNA clone IMAGE:767978 3', 3.69 0.03203913 AA418814 AA418814 mRNA sequence [AA418814] AL356953 leucine-rich repeat-containing G protein-coupled receptor 6 {Homo sapiens} (exp=0; 3.63 0.0277936 THC2705989 wgp=1; cg=0), partial (4%) [THC2752981] AA484677 ne64a07.s1 NCI_CGAP_Alv1 Homo sapiens cDNA clone IMAGE:909012, mRNA 3.63 0.027098073 AA484677 AA484677 sequence [AA484677] oe06h09.s1 NCI_CGAP_Ov2 Homo sapiens cDNA clone IMAGE:1385153, mRNA sequence 3.48 0.04468495 AA837799 AA837799 [AA837799] Homo sapiens hypothetical protein LOC340109, mRNA (cDNA clone IMAGE:5578073), partial 3.27 0.031178378 BC039509 LOC643401 cds. [BC039509] Homo sapiens Fas (TNF receptor superfamily, member 6) (FAS), transcript variant 1, mRNA 3.24 0.022156298 NM_000043 FAS [NM_000043] 3.20 0.021043295 A_32_P125056 BF803942 CM2-CI0135-021100-477-g08 CI0135 Homo sapiens cDNA, mRNA sequence 3.04 0.043389246 BF803942 BF803942 [BF803942] 3.03 0.002430239 NM_015920 RPS27L Homo sapiens ribosomal protein S27-like (RPS27L), mRNA [NM_015920] Homo sapiens tumor necrosis factor receptor superfamily, member 10c, decoy without an 2.98 0.021202829 NM_003841 TNFRSF10C intracellular domain (TNFRSF10C), mRNA [NM_003841] 2.97 0.03243901 AB002384 C6orf32 Homo sapiens mRNA for KIAA0386 gene, partial cds.
    [Show full text]
  • Number 8 August 2015 Atlas of Genetics and Cytogenetics in Oncology and Haematology
    Volume 1 - Number 1 May - September 1997 Volume 19 - Number 8 August 2015 Atlas of Genetics and Cytogenetics in Oncology and Haematology OPEN ACCESS JOURNAL INIST-CNRS Scope The Atlas of Genetics and Cytogenetics in Oncology and Haematologyis a peer reviewed on-line journal in open access, devoted to genes, cytogenetics, and clinical entities in cancer, and cancer-prone diseases. It is made for and by: clinicians and researchers in cytogenetics, molecular biology, oncology, haematology, and pathology. One main scope of the Atlas is to conjugate the scientific information provided by cytogenetics/molecular genetics to the clinical setting (diagnostics, prognostics and therapeutic design), another is to provide an encyclopedic knowledge in cancer genetics. The Atlas deals with cancer research and genomics. It is at the crossroads of research, virtual medical university (university and post-university e-learning), and telemedicine. It contributes to "meta-medicine", this mediation, using information technology, between the increasing amount of knowledge and the individual, having to use the information. Towards a personalized medicine of cancer. It presents structured review articles ("cards") on: 1- Genes, 2- Leukemias, 3- Solid tumors, 4- Cancer-prone diseases, and also 5- "Deep insights": more traditional review articles on the above subjects and on surrounding topics. It also present 6- Case reports in hematology and 7- Educational items in the various related topics for students in Medicine and in Sciences. The Atlas of Genetics and Cytogenetics in Oncology and Haematology does not publish research articles. See also: http://documents.irevues.inist.fr/bitstream/handle/2042/56067/Scope.pdf Editorial correspondance Jean-Loup Huret, MD, PhD, Genetics, Department of Medical Information, University Hospital F-86021 Poitiers, France phone +33 5 49 44 45 46 [email protected] or [email protected] .
    [Show full text]
  • Characterizing Genomic Duplication in Autism Spectrum Disorder by Edward James Higginbotham a Thesis Submitted in Conformity
    Characterizing Genomic Duplication in Autism Spectrum Disorder by Edward James Higginbotham A thesis submitted in conformity with the requirements for the degree of Master of Science Graduate Department of Molecular Genetics University of Toronto © Copyright by Edward James Higginbotham 2020 i Abstract Characterizing Genomic Duplication in Autism Spectrum Disorder Edward James Higginbotham Master of Science Graduate Department of Molecular Genetics University of Toronto 2020 Duplication, the gain of additional copies of genomic material relative to its ancestral diploid state is yet to achieve full appreciation for its role in human traits and disease. Challenges include accurately genotyping, annotating, and characterizing the properties of duplications, and resolving duplication mechanisms. Whole genome sequencing, in principle, should enable accurate detection of duplications in a single experiment. This thesis makes use of the technology to catalogue disease relevant duplications in the genomes of 2,739 individuals with Autism Spectrum Disorder (ASD) who enrolled in the Autism Speaks MSSNG Project. Fine-mapping the breakpoint junctions of 259 ASD-relevant duplications identified 34 (13.1%) variants with complex genomic structures as well as tandem (193/259, 74.5%) and NAHR- mediated (6/259, 2.3%) duplications. As whole genome sequencing-based studies expand in scale and reach, a continued focus on generating high-quality, standardized duplication data will be prerequisite to addressing their associated biological mechanisms. ii Acknowledgements I thank Dr. Stephen Scherer for his leadership par excellence, his generosity, and for giving me a chance. I am grateful for his investment and the opportunities afforded me, from which I have learned and benefited. I would next thank Drs.
    [Show full text]
  • UK Lipoedema’ Cohort
    medRxiv preprint doi: https://doi.org/10.1101/2021.06.15.21258988; this version posted June 18, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted medRxiv a license to display the preprint in perpetuity. It is made available under a CC-BY 4.0 International license . Investigation of clinical characteristics and genome associations in the ‘UK Lipoedema’ cohort Authors Dionysios Grigoriadis1*, Ege Sackey1*, Katie Riches2**, Malou van Zanten1**, Glen Brice3, Ruth England2, Mike Mills1, Sara E Dobbins1, Lipoedema Consortium, Genomics England Research Consortium4, Steve Jeffery1, Liang Dong5, David B. Savage5, Peter S. Mortimer1,6, Vaughan Keeley2,7, Alan Pittman1, Kristiana Gordon1,6 ‡, Pia Ostergaard1 ‡ Affiliations 1. Molecular and Clinical Sciences Institute, St George’s University of London, London, UK 2. University Hospitals of Derby and Burton NHS Foundation Trust, Derby, UK 3. South West Thames Regional Genetics Unit, St George's University of London, London, UK 4. Genomics England, London, UK 5. Metabolic Research Laboratories, Wellcome Trust-Medical Research Council Institute of Metabolic Science, University of Cambridge, Cambridge CB2 0QQ, UK 6. Dermatology & Lymphovascular Medicine, St George's Universities NHS Foundation trust, London, UK 7. University of Nottingham Medical School, Nottingham, UK *These two authors contributed equally; ** These two authors contributed equally ‡Clinical correspondence to Kristiana Gordon [email protected] and research- related correspondence to Pia Ostergaard, [email protected] NOTE: This preprint reports new research that has not been certified by peer review and should not be used to guide clinical practice. 1 medRxiv preprint doi: https://doi.org/10.1101/2021.06.15.21258988; this version posted June 18, 2021.
    [Show full text]