Learning Natural Selection from the Site Frequency Spectrum a Letter Submitted to Genetics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Incorporating Genetic Networks Into Case-Control Association Studies with High-Dimensional DNA Methylation Data Kipoong Kim and Hokeun Sun*
Kim and Sun BMC Bioinformatics (2019) 20:510 https://doi.org/10.1186/s12859-019-3040-x METHODOLOGY ARTICLE Open Access Incorporating genetic networks into case-control association studies with high-dimensional DNA methylation data Kipoong Kim and Hokeun Sun* Abstract Background: In human genetic association studies with high-dimensional gene expression data, it has been well known that statistical selection methods utilizing prior biological network knowledge such as genetic pathways and signaling pathways can outperform other methods that ignore genetic network structures in terms of true positive selection. In recent epigenetic research on case-control association studies, relatively many statistical methods have been proposed to identify cancer-related CpG sites and their corresponding genes from high-dimensional DNA methylation array data. However, most of existing methods are not designed to utilize genetic network information although methylation levels between linked genes in the genetic networks tend to be highly correlated with each other. Results: We propose new approach that combines data dimension reduction techniques with network-based regularization to identify outcome-related genes for analysis of high-dimensional DNA methylation data. In simulation studies, we demonstrated that the proposed approach overwhelms other statistical methods that do not utilize genetic network information in terms of true positive selection. We also applied it to the 450K DNA methylation array data of the four breast invasive carcinoma cancer subtypes from The Cancer Genome Atlas (TCGA) project. Conclusions: The proposed variable selection approach can utilize prior biological network information for analysis of high-dimensional DNA methylation array data. It first captures gene level signals from multiple CpG sites using data a dimension reduction technique and then performs network-based regularization based on biological network graph information. -
Quantitative-PCR Validation of 154 Genomic Segments Called As Cnvs in Five Replicat
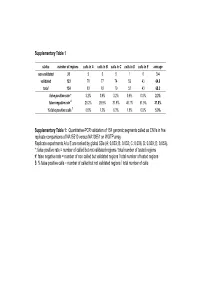
Supplementary Table 1 status number of regions calls in A calls in B calls in C calls in D calls in E average non validated 31 5 6 5 1 0 3.4 validated 123 78 77 74 52 43 64.8 total 154 83 83 79 53 43 68.2 false positive rate * 3.2% 3.9% 3.2% 0.6% 0.0% 2.2% false negative rate # 29.2% 29.9% 31.8% 46.1% 51.9% 37.8% % false positive calls $ 6.0% 7.2% 6.3% 1.9% 0.0% 5.0% Supplementary Table 1: Quantitative-PCR validation of 154 genomic segments called as CNVs in five replicate comparisons of NA15510 versus NA10851 on WGTP array Replicate experiments A to E are ranked by global SDe (A: 0.033; B: 0.033; C: 0.036; D: 0.039; E: 0.053). *: false positive rate = number of called but not validated regions / total number of tested regions #: false negative rate = number of non called but validated regions / total number of tested regions $: % false positive calls = number of called but not validated regions / total number of calls False positive estimates for 500K EA CNV calls Total Rep1 Rep2 Rep3 Avg (unique) Validated 33 28 32 31 38 Not validated 2 2 2 2 5 Total 35 30 34 33 43 % False positive 5.71% 6.67% 5.88% 6.09% - % False negative 13.16% 26.32% 15.79% 18.42% - Supplementary Table 2A : Quantitative PCR validation of 43 unique CNV regions called as CNVs in three replicate comparisons of NA15510 versus NA10851 using the 500K EA array. -

Supplemental Table 1 (S1). the Chromosomal Regions and Genes Exhibiting Loss of Heterozygosity That Were Shared Between the HLRCC-Rccs of Both Patients 1 and 2
BMJ Publishing Group Limited (BMJ) disclaims all liability and responsibility arising from any reliance Supplemental material placed on this supplemental material which has been supplied by the author(s) J Clin Pathol Supplemental Table 1 (S1). The chromosomal regions and genes exhibiting loss of heterozygosity that were shared between the HLRCC-RCCs of both Patients 1 and 2. Chromosome Position Genes 1 p13.1 ATP1A1, ATP1A1-AS1, LOC101929023, CD58, IGSF3, MIR320B1, C1orf137, CD2, PTGFRN, CD101, LOC101929099 1 p21.1* COL11A1, LOC101928436, RNPC3, AMY2B, ACTG1P4, AMY2A, AMY1A, AMY1C, AMY1B 1 p36.11 LOC101928728, ARID1A, PIGV, ZDHHC18, SFN, GPN2, GPATCH3, NR0B2, NUDC, KDF1, TRNP1, FAM46B, SLC9A1, WDTC1, TMEM222, ACTG1P20, SYTL1, MAP3K6, FCN3, CD164L2, GPR3, WASF2, AHDC1, FGR, IFI6 1 q21.3* KCNN3, PMVK, PBXIP1, PYGO2, LOC101928120, SHC1, CKS1B, MIR4258, FLAD1, LENEP, ZBTB7B, DCST2, DCST1, LOC100505666, ADAM15, EFNA4, EFNA3, EFNA1, SLC50A1, DPM3, KRTCAP2, TRIM46, MUC1, MIR92B, THBS3, MTX1, GBAP1, GBA, FAM189B, SCAMP3, CLK2, HCN3, PKLR, FDPS, RUSC1-AS1, RUSC1, ASH1L, MIR555, POU5F1P4, ASH1L-AS1, MSTO1, MSTO2P, YY1AP1, SCARNA26A, DAP3, GON4L, SCARNA26B, SYT11, RIT1, KIAA0907, SNORA80E, SCARNA4, RXFP4, ARHGEF2, MIR6738, SSR2, UBQLN4, LAMTOR2, RAB25, MEX3A, LMNA, SEMA4A, SLC25A44, PMF1, PMF1-BGLAP 1 q24.2–44* LOC101928650, GORAB, PRRX1, MROH9, FMO3, MIR1295A, MIR1295B, FMO6P, FMO2, FMO1, FMO4, TOP1P1, PRRC2C, MYOC, VAMP4, METTL13, DNM3, DNM3-IT1, DNM3OS, MIR214, MIR3120, MIR199A2, C1orf105, PIGC, SUCO, FASLG, TNFSF18, TNFSF4, LOC100506023, LOC101928673, -

Amino Acid Sequences Directed Against Cxcr4 And
(19) TZZ ¥¥_T (11) EP 2 285 833 B1 (12) EUROPEAN PATENT SPECIFICATION (45) Date of publication and mention (51) Int Cl.: of the grant of the patent: C07K 16/28 (2006.01) A61K 39/395 (2006.01) 17.12.2014 Bulletin 2014/51 A61P 31/18 (2006.01) A61P 35/00 (2006.01) (21) Application number: 09745851.7 (86) International application number: PCT/EP2009/056026 (22) Date of filing: 18.05.2009 (87) International publication number: WO 2009/138519 (19.11.2009 Gazette 2009/47) (54) AMINO ACID SEQUENCES DIRECTED AGAINST CXCR4 AND OTHER GPCRs AND COMPOUNDS COMPRISING THE SAME GEGEN CXCR4 UND ANDERE GPCR GERICHTETE AMINOSÄURESEQUENZEN SOWIE VERBINDUNGEN DAMIT SÉQUENCES D’ACIDES AMINÉS DIRIGÉES CONTRE CXCR4 ET AUTRES GPCR ET COMPOSÉS RENFERMANT CES DERNIÈRES (84) Designated Contracting States: (74) Representative: Hoffmann Eitle AT BE BG CH CY CZ DE DK EE ES FI FR GB GR Patent- und Rechtsanwälte PartmbB HR HU IE IS IT LI LT LU LV MC MK MT NL NO PL Arabellastraße 30 PT RO SE SI SK TR 81925 München (DE) (30) Priority: 16.05.2008 US 53847 P (56) References cited: 02.10.2008 US 102142 P EP-A- 1 316 801 WO-A-99/50461 WO-A-03/050531 WO-A-03/066830 (43) Date of publication of application: WO-A-2006/089141 WO-A-2007/051063 23.02.2011 Bulletin 2011/08 • VADAY GAYLE G ET AL: "CXCR4 and CXCL12 (73) Proprietor: Ablynx N.V. (SDF-1) in prostate cancer: inhibitory effects of 9052 Ghent-Zwijnaarde (BE) human single chain Fv antibodies" CLINICAL CANCER RESEARCH, THE AMERICAN (72) Inventors: ASSOCIATION FOR CANCER RESEARCH, US, • BLANCHETOT, Christophe vol.10, no. -

Us 2018 / 0305689 A1
US 20180305689A1 ( 19 ) United States (12 ) Patent Application Publication ( 10) Pub . No. : US 2018 /0305689 A1 Sætrom et al. ( 43 ) Pub . Date: Oct. 25 , 2018 ( 54 ) SARNA COMPOSITIONS AND METHODS OF plication No . 62 /150 , 895 , filed on Apr. 22 , 2015 , USE provisional application No . 62/ 150 ,904 , filed on Apr. 22 , 2015 , provisional application No. 62 / 150 , 908 , (71 ) Applicant: MINA THERAPEUTICS LIMITED , filed on Apr. 22 , 2015 , provisional application No. LONDON (GB ) 62 / 150 , 900 , filed on Apr. 22 , 2015 . (72 ) Inventors : Pål Sætrom , Trondheim (NO ) ; Endre Publication Classification Bakken Stovner , Trondheim (NO ) (51 ) Int . CI. C12N 15 / 113 (2006 .01 ) (21 ) Appl. No. : 15 /568 , 046 (52 ) U . S . CI. (22 ) PCT Filed : Apr. 21 , 2016 CPC .. .. .. C12N 15 / 113 ( 2013 .01 ) ; C12N 2310 / 34 ( 2013. 01 ) ; C12N 2310 /14 (2013 . 01 ) ; C12N ( 86 ) PCT No .: PCT/ GB2016 /051116 2310 / 11 (2013 .01 ) $ 371 ( c ) ( 1 ) , ( 2 ) Date : Oct . 20 , 2017 (57 ) ABSTRACT The invention relates to oligonucleotides , e . g . , saRNAS Related U . S . Application Data useful in upregulating the expression of a target gene and (60 ) Provisional application No . 62 / 150 ,892 , filed on Apr. therapeutic compositions comprising such oligonucleotides . 22 , 2015 , provisional application No . 62 / 150 ,893 , Methods of using the oligonucleotides and the therapeutic filed on Apr. 22 , 2015 , provisional application No . compositions are also provided . 62 / 150 ,897 , filed on Apr. 22 , 2015 , provisional ap Specification includes a Sequence Listing . SARNA sense strand (Fessenger 3 ' SARNA antisense strand (Guide ) Mathew, Si Target antisense RNA transcript, e . g . NAT Target Coding strand Gene Transcription start site ( T55 ) TY{ { ? ? Targeted Target transcript , e . -

OR2L8 Sirna (H): Sc-88208
SANTA CRUZ BIOTECHNOLOGY, INC. OR2L8 siRNA (h): sc-88208 BACKGROUND PRODUCT Chromosome 1 is the largest human chromosome spanning about 260 million OR2L8 siRNA (h) is a pool of 2 target-specific 19-25 nt siRNAs designed to base pairs and making up 8% of the human genome. There are about 3,000 knock down gene expression. Each vial contains 3.3 nmol of lyophilized genes on chromosome 1, and considering the great number of genes there are siRNA, sufficient for a 10 µM solution once resuspended using protocol also a large number of diseases associated with chromosome 1. Notably, the below. Suitable for 50-100 transfections. Also see OR2L8 shRNA Plasmid (h): rare aging disease Hutchinson-Gilford progeria is associated with the LMNA sc-88208-SH and OR2L8 shRNA (h) Lentiviral Particles: sc-88208-V as alter- gene which encodes Lamin A. When defective, the LMNA gene product can nate gene silencing products. build up in the nucleus and cause characteristic nuclear blebs. The mechanism For independent verification of OR2L8 (h) gene silencing results, we also of rapidly enhanced aging is unclear and is a topic of continuing exploration. provide the individual siRNA duplex components. Each is available as The MUTYH gene is located on chromosome 1 and is partially responsible for 3.3 nmol of lyophilized siRNA. These include: sc-88208A and sc-88208B. familial adenomatous polyposis. Stickler syndrome, Parkinsons, Gaucher dis- ease and Usher syndrome are also associated with chromosome 1. A break- STORAGE AND RESUSPENSION point has been identified in 1q which disrupts the DISC1 gene and is linked to schizophrenia. -
The Spectra of Somatic Mutations Across Many Tumor Types
The spectra of somatic mutations across many tumor types Mike Lawrence Broad Institute of Harvard and MIT 1st Annual TCGA Scientific Symposium November 17, 2011 mutation rates across cancer Hematologic Carcinogens Childhood ?? ?? HPV & HPV mutation type C → T C → A C → G A → G A → T A → C OV mutation type C → T C → A C → G A → G A → T A → C mutation rate (per million sites) OV mutation type C → T C → A C → G A → G A → T A → C mutation rate (per million sites) GBM mutation type C → T C → A C → G A → G A → T A → C LUSC lung squamous mutation type C → T C → A C → G A → G A → T A → C LUAD lung adeno mutation type C → T C → A C → G A → G A → T A → C Melanoma mutation type C → T C → A C → G A → G A → T A → C cervical mutation type C → T C → A C → G A → G A → T A → C bladder total rate 100/Mb 10/Mb 1/Mb 0.1/Mb total rate type of spectrum Head&Neck HPV GBM HPV Bladder viral? Kidney Esophageal Colorectal Gastric Lung Melanoma GBM Kidney H&N Bladder Lung Gastric Colorectal Esophageal Melanoma finding significantly mutated genes patients tally significance MutSig scoring algorithm genes * patients tally significance MutSig scoring algorithm version 0 assume background mutation rate is: genes · uniform across sequence contexts · uniform across patients · uniform across genes * patients tally significance MutSig scoring algorithm version 1 assume background mutation rate is: genes · variable across sequence contexts · uniform across patients · uniform across genes * C→T (UV-induced) A→T patients tally significance MutSig scoring algorithm version -

Novel Cell Lines and Methods
(19) TZZ¥ZZ_¥_T (11) EP 3 009 513 A1 (12) EUROPEAN PATENT APPLICATION (43) Date of publication: (51) Int Cl.: 20.04.2016 Bulletin 2016/16 C12N 15/85 (2006.01) C12N 15/67 (2006.01) C07K 14/435 (2006.01) (21) Application number: 15180871.4 (22) Date of filing: 02.02.2009 (84) Designated Contracting States: (72) Inventor: SHEKDAR, Kambiz AT BE BG CH CY CZ DE DK EE ES FI FR GB GR New York, NY 10010 (US) HR HU IE IS IT LI LT LU LV MC MK MT NL NO PL PT RO SE SI SK TR (74) Representative: Vossius & Partner Patentanwälte Rechtsanwälte mbB (30) Priority: 01.02.2008 US 63219 P Siebertstrasse 3 81675 München (DE) (62) Document number(s) of the earlier application(s) in accordance with Art. 76 EPC: Remarks: 09709529.3 / 2 245 171 •Claims filed after the date of filing of the application (Rule 68(4) EPC). (71) Applicant: Chromocell Corporation •This application was filed on 13-08-2015 as a North Brunswick, NJ 08902 (US) divisional application to the application mentioned under INID code 62. (54) NOVEL CELL LINES AND METHODS (57) The invention relates to novel cells and cell lines, and methods for making and using them. EP 3 009 513 A1 Printed by Jouve, 75001 PARIS (FR) EP 3 009 513 A1 Description Field of the Invention 5 [0001] The invention relates to novel cells and cell lines, and methods for making and using them. Background of the Invention [0002] Currently, the industry average failure rate for drug discovery programs in pharmaceutical companies is reported 10 to be approximately 98%. -

Supplemental Table 1 (S1). the Chromosomal Regions and Genes Exhibiting Loss of Heterozygosity That Were Shared Between the HLRCC-Rccs of Both Patients 1 and 2
Supplementary material J Clin Pathol Supplemental Table 1 (S1). The chromosomal regions and genes exhibiting loss of heterozygosity that were shared between the HLRCC-RCCs of both Patients 1 and 2. Chromosome Position Genes 1 p13.1 ATP1A1, ATP1A1-AS1, LOC101929023, CD58, IGSF3, MIR320B1, C1orf137, CD2, PTGFRN, CD101, LOC101929099 1 p21.1* COL11A1, LOC101928436, RNPC3, AMY2B, ACTG1P4, AMY2A, AMY1A, AMY1C, AMY1B 1 p36.11 LOC101928728, ARID1A, PIGV, ZDHHC18, SFN, GPN2, GPATCH3, NR0B2, NUDC, KDF1, TRNP1, FAM46B, SLC9A1, WDTC1, TMEM222, ACTG1P20, SYTL1, MAP3K6, FCN3, CD164L2, GPR3, WASF2, AHDC1, FGR, IFI6 1 q21.3* KCNN3, PMVK, PBXIP1, PYGO2, LOC101928120, SHC1, CKS1B, MIR4258, FLAD1, LENEP, ZBTB7B, DCST2, DCST1, LOC100505666, ADAM15, EFNA4, EFNA3, EFNA1, SLC50A1, DPM3, KRTCAP2, TRIM46, MUC1, MIR92B, THBS3, MTX1, GBAP1, GBA, FAM189B, SCAMP3, CLK2, HCN3, PKLR, FDPS, RUSC1-AS1, RUSC1, ASH1L, MIR555, POU5F1P4, ASH1L-AS1, MSTO1, MSTO2P, YY1AP1, SCARNA26A, DAP3, GON4L, SCARNA26B, SYT11, RIT1, KIAA0907, SNORA80E, SCARNA4, RXFP4, ARHGEF2, MIR6738, SSR2, UBQLN4, LAMTOR2, RAB25, MEX3A, LMNA, SEMA4A, SLC25A44, PMF1, PMF1-BGLAP 1 q24.2–44* LOC101928650, GORAB, PRRX1, MROH9, FMO3, MIR1295A, MIR1295B, FMO6P, FMO2, FMO1, FMO4, TOP1P1, PRRC2C, MYOC, VAMP4, METTL13, DNM3, DNM3-IT1, DNM3OS, MIR214, MIR3120, MIR199A2, C1orf105, PIGC, SUCO, FASLG, TNFSF18, TNFSF4, LOC100506023, LOC101928673, PRDX6, SLC9C2, ANKRD45, LOC730159, KLHL20, CENPL, DARS2, GAS5- AS1, GAS5, SNORD81, SNORD47, SNORD80, SNORD79, SNORD78, SNORD44, SNORA103, SNORD77, SNORD76, SNORD75, SNORD74, -

Online Supporting Information S1: Proteins in Each Positive Regulatory Pathway
Online Supporting Information S1: Proteins in each positive regulatory pathway Index Proteins DLD,GCK,GPI,HK1,HK2,HK3,ACSS1,ACSS2,ADH1A,ADH1B,ADH4,ADH5,ADH6,ADH7,AK R1A1,ALDH1A3,ALDH1B1,ALDH2,ALDH3A1,ALDH3A2,ALDH3B1,ALDH3B2,ALDH7A1,ALD Positive_1 H9A1,ALDOA,ALDOB,ALDOC,BPGM,DLAT,ENO1,ENO2,ENO3,FBP1,FBP2,G6PC,G6PC2,G ALM,GAPDH,LDHA,LDHAL6A,LDHAL6B,LDHB,LDHC,PCK1,PCK2,PDHA1,PDHA2,PDHB,PF KL,PFKM,PFKP,PGAM1,PGAM2,PGAM4,PGK1,PGK2,PGM1,PGM3,PKLR,PKM2,TPI1 CS,DLD,FH,PC,ACLY,ACO1,ACO2,DLAT,DLST,IDH1,IDH2,IDH3A,IDH3B,IDH3G,MDH1 Positive_2 ,MDH2,OGDH,OGDHL,PCK1,PCK2,PDHA1,PDHA2,PDHB,SDHA,SDHB,SDHC,SDHD,SUCLA2 ,SUCLG1,SUCLG2 GPI,PGD,RPE,TKT,ALDOA,ALDOB,ALDOC,DERA,FBP1,FBP2,G6PD,H6PD,PFKL,PFKM,P Positive_3 FKP,PGLS,PGM1,PGM3,PRPS1,PRPS2,RBKS,RPIA,TALDO1,TKTL1,TKTL2 RPE,AKR1B1,DCXR,GUSB,UGDH,UGP2,UGT1A10,UGT2A1,UGT2A3,UGT2B10,UGT2B11,U Positive_4 GT2B17,UGT2B28,UGT2B4,UGT2B7,XYLB FUK,GCK,HK1,HK2,HK3,KHK,MPI,AKR1B1,ALDOA,ALDOB,ALDOC,FBP1,FBP2,FPGT,GM Positive_5 DS,GMPPA,GMPPB,MTMR1,MTMR2,MTMR6,PFKFB1,PFKFB2,PFKFB3,PFKFB4,PFKL,PFKM ,PFKP,PGM2,PHPT1,PMM1,PMM2,SORD,TPI1,TSTA3,UGCGL1,UGCGL2 GAA,GCK,GLA,HK1,HK2,HK3,LCT,AKR1B1,B4GALT1,B4GALT2,G6PC,G6PC2,GALE,GAL Positive_6 K1,GALK2,GALT,GANC,GLB1,LALBA,MGAM,PGM1,PGM3,UGP2 Positive_7 ACACA,ACACB,FASN,MCAT,OLAH,OXSM Positive_8 ACAA2,ECHS1,HADH,HADHA,HADHB,HSD17B4,MECR,PPT1,HSD17B10 ACAA1,ACAA2,ACADL,ACADM,ACADS,ACADSB,ACADVL,ACAT1,ACAT2,ACOX1,ACOX3,AC SL1,ACSL3,ACSL4,ACSL5,ACSL6,ADH1A,ADH1B,ADH4,ADH5,ADH6,ADH7,ALDH1A3,AL Positive_9 DH1B1,ALDH2,ALDH3A1,ALDH3A2,ALDH7A1,ALDH9A1,CPT1A,CPT1B,CPT1C,CPT2,CYP 4A11,CYP4A22,ECHS1,EHHADH,GCDH,HADH,HADHA,HADHB,HSD17B4,HSD17B10 -
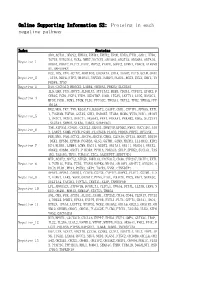
Online Supporting Information S2: Proteins in Each Negative Pathway
Online Supporting Information S2: Proteins in each negative pathway Index Proteins ADO,ACTA1,DEGS2,EPHA3,EPHB4,EPHX2,EPOR,EREG,FTH1,GAD1,HTR6, IGF1R,KIR2DL4,NCR3,NME7,NOTCH1,OR10S1,OR2T33,OR56B4,OR7A10, Negative_1 OR8G1,PDGFC,PLCZ1,PROC,PRPS2,PTAFR,SGPP2,STMN1,VDAC3,ATP6V0 A1,MAPKAPK2 DCC,IDS,VTN,ACTN2,AKR1B10,CACNA1A,CHIA,DAAM2,FUT5,GCLM,GNAZ Negative_2 ,ITPA,NEU4,NTF3,OR10A3,PAPSS1,PARD3,PLOD1,RGS3,SCLY,SHC1,TN FRSF4,TP53 Negative_3 DAO,CACNA1D,HMGCS2,LAMB4,OR56A3,PRKCQ,SLC25A5 IL5,LHB,PGD,ADCY3,ALDH1A3,ATP13A2,BUB3,CD244,CYFIP2,EPHX2,F CER1G,FGD1,FGF4,FZD9,HSD17B7,IL6R,ITGAV,LEFTY1,LIPG,MAN1C1, Negative_4 MPDZ,PGM1,PGM3,PIGM,PLD1,PPP3CC,TBXAS1,TKTL2,TPH2,YWHAQ,PPP 1R12A HK2,MOS,TKT,TNN,B3GALT4,B3GAT3,CASP7,CDH1,CYFIP1,EFNA5,EXTL 1,FCGR3B,FGF20,GSTA5,GUK1,HSD3B7,ITGB4,MCM6,MYH3,NOD1,OR10H Negative_5 1,OR1C1,OR1E1,OR4C11,OR56A3,PPA1,PRKAA1,PRKAB2,RDH5,SLC27A1 ,SLC2A4,SMPD2,STK36,THBS1,SERPINC1 TNR,ATP5A1,CNGB1,CX3CL1,DEGS1,DNMT3B,EFNB2,FMO2,GUCY1B3,JAG Negative_6 2,LARS2,NUMB,PCCB,PGAM1,PLA2G1B,PLOD2,PRDX6,PRPS1,RFXANK FER,MVD,PAH,ACTC1,ADCY4,ADCY8,CBR3,CLDN16,CPT1A,DDOST,DDX56 ,DKK1,EFNB1,EPHA8,FCGR3A,GLS2,GSTM1,GZMB,HADHA,IL13RA2,KIR2 Negative_7 DS4,KLRK1,LAMB4,LGMN,MAGI1,NUDT2,OR13A1,OR1I1,OR4D11,OR4X2, OR6K2,OR8B4,OXCT1,PIK3R4,PPM1A,PRKAG3,SELP,SPHK2,SUCLG1,TAS 1R2,TAS1R3,THY1,TUBA1C,ZIC2,AASDHPPT,SERPIND1 MTR,ACAT2,ADCY2,ATP5D,BMPR1A,CACNA1E,CD38,CYP2A7,DDIT4,EXTL Negative_8 1,FCER1G,FGD3,FZD5,ITGAM,MAPK8,NR4A1,OR10V1,OR4F17,OR52D1,O R8J3,PLD1,PPA1,PSEN2,SKP1,TACR3,VNN1,CTNNBIP1 APAF1,APOA1,CARD11,CCDC6,CSF3R,CYP4F2,DAPK1,FLOT1,GSTM1,IL2 -

Predictions of Response to Cancer Immunotherapy Via Tumour Mutational Burden and Genomic Resistance Markers Jacob Bradley1 and Nirmesh Patel Phd2
Predictions of Response to Cancer Immunotherapy via Tumour Mutational Burden and Genomic Resistance Markers Jacob Bradley1 and Nirmesh Patel PhD2 1Student: Part III Systems Biology, University of Cambridge, UK 2Supervisor: Cambridge Cancer Genomics, Cambridge, UK ABSTRACT The field of immuno-oncology (IO) is making huge advances translating immunological research into successful therapies, in particular Immune Checkpoint Blockade (ICB). The best predictor of treatment effectiveness in most cancers is the metric of Tumour Mutation Burden (TMB). We consider here methods for constructing a cost-effectively concise gene panel to predict TMB. We then investigate the extent to which it is feasible to produce a single gene panel capable of predicting TMB across a range of cancer types, and methods by which one may attempt to do so. We also look into IO resistance mechanisms and genes associated with poor response to ICB, so that we can ensure the best treatment monitoring possible. Finally, we exhibit an IO monitoring panel for Non-Small Cell Lung Cancer, and analyse its performance in comparison to other commercially available assays. Contents 1 List of Abbreviations 2 2 Introduction 3 2.1 Cancer is a Disease of the Genome.......................................................3 2.2 Immune Responses to Cancer are Mediated by Checkpoints.......................................3 2.3 Immunotherapy is an Emerging Field......................................................4 2.4 Tumour Mutational Burden is a Genomic Biomarker for Immunnotherapy Response........................4 2.5 TMB Varies Across and Within Cancer Types.................................................4 3 Results 5 3.1 TMB Estimation in a Single Cancer Type...................................................5 Genome-Wide Association • Gene Oriented Methods 3.2 TMB Estimation Across Cancer Types....................................................