Embedded Star Clusters As Sources of High-Energy Cosmic Rays Modelling and Constraints
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Ghost Hunt Challenge 2020
Virtual Ghost Hunt Challenge 10/21 /2020 (Sorry we can meet in person this year or give out awards but try doing this challenge on your own.) Participant’s Name _________________________ Categories for the competition: Manual Telescope Electronically Aided Telescope Binocular Astrophotography (best photo) (if you expect to compete in more than one category please fill-out a sheet for each) ** There are four objects on this list that may be beyond the reach of beginning astronomers or basic telescopes. Therefore, we have marked these objects with an * and provided alternate replacements for you just below the designated entry. We will use the primary objects to break a tie if that’s needed. Page 1 TAS Ghost Hunt Challenge - Page 2 Time # Designation Type Con. RA Dec. Mag. Size Common Name Observed Facing West – 7:30 8:30 p.m. 1 M17 EN Sgr 18h21’ -16˚11’ 6.0 40’x30’ Omega Nebula 2 M16 EN Ser 18h19’ -13˚47 6.0 17’ by 14’ Ghost Puppet Nebula 3 M10 GC Oph 16h58’ -04˚08’ 6.6 20’ 4 M12 GC Oph 16h48’ -01˚59’ 6.7 16’ 5 M51 Gal CVn 13h30’ 47h05’’ 8.0 13.8’x11.8’ Whirlpool Facing West - 8:30 – 9:00 p.m. 6 M101 GAL UMa 14h03’ 54˚15’ 7.9 24x22.9’ 7 NGC 6572 PN Oph 18h12’ 06˚51’ 7.3 16”x13” Emerald Eye 8 NGC 6426 GC Oph 17h46’ 03˚10’ 11.0 4.2’ 9 NGC 6633 OC Oph 18h28’ 06˚31’ 4.6 20’ Tweedledum 10 IC 4756 OC Ser 18h40’ 05˚28” 4.6 39’ Tweedledee 11 M26 OC Sct 18h46’ -09˚22’ 8.0 7.0’ 12 NGC 6712 GC Sct 18h54’ -08˚41’ 8.1 9.8’ 13 M13 GC Her 16h42’ 36˚25’ 5.8 20’ Great Hercules Cluster 14 NGC 6709 OC Aql 18h52’ 10˚21’ 6.7 14’ Flying Unicorn 15 M71 GC Sge 19h55’ 18˚50’ 8.2 7’ 16 M27 PN Vul 20h00’ 22˚43’ 7.3 8’x6’ Dumbbell Nebula 17 M56 GC Lyr 19h17’ 30˚13 8.3 9’ 18 M57 PN Lyr 18h54’ 33˚03’ 8.8 1.4’x1.1’ Ring Nebula 19 M92 GC Her 17h18’ 43˚07’ 6.44 14’ 20 M72 GC Aqr 20h54’ -12˚32’ 9.2 6’ Facing West - 9 – 10 p.m. -

February 14, 2015 7:00Pm at the Herrett Center for Arts & Science Colleagues, College of Southern Idaho
Snake River Skies The Newsletter of the Magic Valley Astronomical Society www.mvastro.org Membership Meeting President’s Message Saturday, February 14, 2015 7:00pm at the Herrett Center for Arts & Science Colleagues, College of Southern Idaho. Public Star Party Follows at the It’s that time of year when obstacles appear in the sky. In particular, this year is Centennial Obs. loaded with fog. It got in the way of letting us see the dance of the Jovian moons late last month, and it’s hindered our views of other unique shows. Still, members Club Officers reported finding enough of a clear sky to let us see Comet Lovejoy, and some great photos by members are popping up on the Facebook page. Robert Mayer, President This month, however, is a great opportunity to see the benefit of something [email protected] getting in the way. Our own Chris Anderson of the Herrett Center has been using 208-312-1203 the Centennial Observatory’s scope to do work on occultation’s, particularly with asteroids. This month’s MVAS meeting on Feb. 14th will give him the stage to Terry Wofford, Vice President show us just how this all works. [email protected] The following weekend may also be the time the weather allows us to resume 208-308-1821 MVAS-only star parties. Feb. 21 is a great window for a possible star party; we’ll announce the location if the weather permits. However, if we don’t get that Gary Leavitt, Secretary window, we’ll fall back on what has become a MVAS tradition: Planetarium night [email protected] at the Herrett Center. -

A Basic Requirement for Studying the Heavens Is Determining Where In
Abasic requirement for studying the heavens is determining where in the sky things are. To specify sky positions, astronomers have developed several coordinate systems. Each uses a coordinate grid projected on to the celestial sphere, in analogy to the geographic coordinate system used on the surface of the Earth. The coordinate systems differ only in their choice of the fundamental plane, which divides the sky into two equal hemispheres along a great circle (the fundamental plane of the geographic system is the Earth's equator) . Each coordinate system is named for its choice of fundamental plane. The equatorial coordinate system is probably the most widely used celestial coordinate system. It is also the one most closely related to the geographic coordinate system, because they use the same fun damental plane and the same poles. The projection of the Earth's equator onto the celestial sphere is called the celestial equator. Similarly, projecting the geographic poles on to the celest ial sphere defines the north and south celestial poles. However, there is an important difference between the equatorial and geographic coordinate systems: the geographic system is fixed to the Earth; it rotates as the Earth does . The equatorial system is fixed to the stars, so it appears to rotate across the sky with the stars, but of course it's really the Earth rotating under the fixed sky. The latitudinal (latitude-like) angle of the equatorial system is called declination (Dec for short) . It measures the angle of an object above or below the celestial equator. The longitud inal angle is called the right ascension (RA for short). -

Meeting Program
A A S MEETING PROGRAM 211TH MEETING OF THE AMERICAN ASTRONOMICAL SOCIETY WITH THE HIGH ENERGY ASTROPHYSICS DIVISION (HEAD) AND THE HISTORICAL ASTRONOMY DIVISION (HAD) 7-11 JANUARY 2008 AUSTIN, TX All scientific session will be held at the: Austin Convention Center COUNCIL .......................... 2 500 East Cesar Chavez St. Austin, TX 78701 EXHIBITS ........................... 4 FURTHER IN GRATITUDE INFORMATION ............... 6 AAS Paper Sorters SCHEDULE ....................... 7 Rachel Akeson, David Bartlett, Elizabeth Barton, SUNDAY ........................17 Joan Centrella, Jun Cui, Susana Deustua, Tapasi Ghosh, Jennifer Grier, Joe Hahn, Hugh Harris, MONDAY .......................21 Chryssa Kouveliotou, John Martin, Kevin Marvel, Kristen Menou, Brian Patten, Robert Quimby, Chris Springob, Joe Tenn, Dirk Terrell, Dave TUESDAY .......................25 Thompson, Liese van Zee, and Amy Winebarger WEDNESDAY ................77 We would like to thank the THURSDAY ................. 143 following sponsors: FRIDAY ......................... 203 Elsevier Northrop Grumman SATURDAY .................. 241 Lockheed Martin The TABASGO Foundation AUTHOR INDEX ........ 242 AAS COUNCIL J. Craig Wheeler Univ. of Texas President (6/2006-6/2008) John P. Huchra Harvard-Smithsonian, President-Elect CfA (6/2007-6/2008) Paul Vanden Bout NRAO Vice-President (6/2005-6/2008) Robert W. O’Connell Univ. of Virginia Vice-President (6/2006-6/2009) Lee W. Hartman Univ. of Michigan Vice-President (6/2007-6/2010) John Graham CIW Secretary (6/2004-6/2010) OFFICERS Hervey (Peter) STScI Treasurer Stockman (6/2005-6/2008) Timothy F. Slater Univ. of Arizona Education Officer (6/2006-6/2009) Mike A’Hearn Univ. of Maryland Pub. Board Chair (6/2005-6/2008) Kevin Marvel AAS Executive Officer (6/2006-Present) Gary J. Ferland Univ. of Kentucky (6/2007-6/2008) Suzanne Hawley Univ. -

Star Formation Associated with H II Regions
Bull. Astr. Soc. India (2006) 34, 111{117 Star formation associated with H II regions Katsuo Ogura¤ Kokugakuin University, Higashi, Shibuya-ku, Tokyo 150-8440, Japan Abstract. Star formation associated with H II regions is briefly reviewed. Special emphasis is laid on our series of observational studies on bright-rimmed clouds (BRCs), in which we found a phenomenon called \small-scale sequential star formation." In addition a new hypothesis is advocated on the two modes of star formation associated with H II regions, i.e., the cluster and dispersed modes. The former gives birth to a rich cluster and in the associated H II region BRCs are formed only at a later stage of its evolution in the peripheries. In the latter mode no clusters or only loose ones are formed, but BRCs can appear at earlier stages in inner part of the H II region. Presumably these modes depend on the initial density distribution of the natal molecular cloud. Keywords : H II regions { ISM: globules { stars: formation { OB associations 1. Introduction { Bright-rimmed clouds Bright-rimmed clouds (BRCs), or cometary globules, are small molecular clouds found in and around H II regions (H IIRs) and surrounded often on three sides by ionized gas. They are a sort of remnants of star formation activity associated with H IIRs, because they correspond to relatively dense clumps in the giant molecular cloud left unionized in the course of the expansion of the H IIR. But, at the same time, they are current sites of star formation. Theoretically, triggered star formation caused by the compression of the gas due to shock is expected to take place in such a con¯guration of the ionization front. -

Atlas Menor Was Objects to Slowly Change Over Time
C h a r t Atlas Charts s O b by j Objects e c t Constellation s Objects by Number 64 Objects by Type 71 Objects by Name 76 Messier Objects 78 Caldwell Objects 81 Orion & Stars by Name 84 Lepus, circa , Brightest Stars 86 1720 , Closest Stars 87 Mythology 88 Bimonthly Sky Charts 92 Meteor Showers 105 Sun, Moon and Planets 106 Observing Considerations 113 Expanded Glossary 115 Th e 88 Constellations, plus 126 Chart Reference BACK PAGE Introduction he night sky was charted by western civilization a few thou - N 1,370 deep sky objects and 360 double stars (two stars—one sands years ago to bring order to the random splatter of stars, often orbits the other) plotted with observing information for T and in the hopes, as a piece of the puzzle, to help “understand” every object. the forces of nature. The stars and their constellations were imbued with N Inclusion of many “famous” celestial objects, even though the beliefs of those times, which have become mythology. they are beyond the reach of a 6 to 8-inch diameter telescope. The oldest known celestial atlas is in the book, Almagest , by N Expanded glossary to define and/or explain terms and Claudius Ptolemy, a Greco-Egyptian with Roman citizenship who lived concepts. in Alexandria from 90 to 160 AD. The Almagest is the earliest surviving astronomical treatise—a 600-page tome. The star charts are in tabular N Black stars on a white background, a preferred format for star form, by constellation, and the locations of the stars are described by charts. -

SAA 100 Club
S.A.A. 100 Observing Club Raleigh Astronomy Club Version 1.2 07-AUG-2005 Introduction Welcome to the S.A.A. 100 Observing Club! This list started on the USENET newsgroup sci.astro.amateur when someone asked about everyone’s favorite, non-Messier objects for medium sized telescopes (8-12”). The members of the group nominated objects and voted for their favorites. The top 100 objects, by number of votes, were collected and ranked into a list that was published. This list is a good next step for someone who has observed all the objects on the Messier list. Since it includes objects in both the Northern and Southern Hemispheres (DEC +72 to -72), the award has two different levels to accommodate those observers who aren't able to travel. The first level, the Silver SAA 100 award requires 88 objects (all visible from North Carolina). The Gold SAA 100 Award requires all 100 objects to be observed. One further note, many of these objects are on other observing lists, especially Patrick Moore's Caldwell list. For convenience, there is a table mapping various SAA100 objects with their Caldwell counterparts. This will facilitate observers who are working or have worked on these lists of objects. We hope you enjoy looking at all the great objects recommended by other avid astronomers! Rules In order to earn the Silver certificate for the program, the applicant must meet the following qualifications: 1. Be a member in good standing of the Raleigh Astronomy Club. 2. Observe 80 Silver observations. 3. Record the time and date of each observation. -

The Desert Sky Observer
Desert Sky Observer Volume 35 Antelope Valley Astronomy Club Newsletter February 2015 Up-Coming Events February 7: Prime Desert Moon Walk February 13: Club Meeting* February 21: Dark Sky Star Party @ TBA * Monthly meetings are held at the S.A.G.E. Planetarium on the Cactus School campus in Palmdale, the second Friday of each month. The meeting location is at the northeast corner of Avenue R and 20th Street East. Meetings start at 7 p.m. and are open to the public. Please note that food and drink are not allowed in the planetarium President Frank Moore Headline January 26, 2015. Giant asteroid makes close pass of earth. Visible to amateur astronomers with modest sized telescopes. Clouds move in to cover the view in Southern California….of course. President of Antelope Valley Astronomy Club fields questions from people asking if the asteroid is causing the “historic blizzard” on the East Coast. President says, in a word, “NO!!” though many callers are still skeptical. There you have it fellow AVAC members, today’s current events in a nutshell. In other recent news of astronomical interest, on January 23 we had three moons of Jupiter transit across the face of the giant planet. Weather permitting, this should have been visible to amateur astronomers with mid-sized telescopes. I set up our C-11 in the afternoon and got ready for what, we expected, would be a great night of observing not just Jupiter, but also other celestial wonders. Once it got dark enough I did a polar alignment, a three star alignment, and threw in a few calibration stars to boot. -

Embedded Star Clusters As Sources of High-Energy Cosmic Rays: Modelling and Constraints
Astronomy & Astrophysics manuscript no. ESC c ESO 2018 October 16, 2018 Embedded star clusters as sources of high-energy cosmic rays Modelling and constraints G. Maurin1, A. Marcowith2, N. Komin3, F. Krayzel1, and G. Lamanna1 1Laboratoire d’Annecy-le-Vieux de Physique des Particules, Université Savoie Mont-Blanc, CNRS/IN2P3, F-74941 Annecy-le- Vieux, France 2Laboratoire Univers et Particules de Montpellier, Université Montpellier 2, CNRS/IN2P3, CC 72, Place Eugène Bataillon, F-34095 Montpellier Cedex 5, France 3School of Physics, University of the Witwatersrand, 1 Jan Smuts Avenue, Braamfontein, Johannesburg, 2050 South Africa Received DAY MONTH 2016; accepted DAY MONTH 2016 ABSTRACT Context. Massive stars are mainly found in stellar associations. These massive star clusters occur in the heart of giant molecular clouds. The strong stellar wind activity in these objects generates large bubbles and induces collective effects that could accelerate particles up to high energy and produce γ-rays. The best way to input an acceleration origin to the stellar wind interaction in massive stellar cluster is to observe young massive star clusters in which no supernova explosion has occurred yet. Aims. This work aims to constrain the part of stellar wind mechanical energy that is converted into energetic particles using the sensitivity of the ongoing Fermi-LAT instrument. This work further provides detailed predictions of expected γ-ray fluxes in the view of the on-set of the next generation of imaging atmospheric Cherenkov telescopes. Methods. A one-zone model where energetic particles are accelerated by repeated interactions with strong supersonic shocks occur- ring in massive star clusters was developed. -

Making a Sky Atlas
Appendix A Making a Sky Atlas Although a number of very advanced sky atlases are now available in print, none is likely to be ideal for any given task. Published atlases will probably have too few or too many guide stars, too few or too many deep-sky objects plotted in them, wrong- size charts, etc. I found that with MegaStar I could design and make, specifically for my survey, a “just right” personalized atlas. My atlas consists of 108 charts, each about twenty square degrees in size, with guide stars down to magnitude 8.9. I used only the northernmost 78 charts, since I observed the sky only down to –35°. On the charts I plotted only the objects I wanted to observe. In addition I made enlargements of small, overcrowded areas (“quad charts”) as well as separate large-scale charts for the Virgo Galaxy Cluster, the latter with guide stars down to magnitude 11.4. I put the charts in plastic sheet protectors in a three-ring binder, taking them out and plac- ing them on my telescope mount’s clipboard as needed. To find an object I would use the 35 mm finder (except in the Virgo Cluster, where I used the 60 mm as the finder) to point the ensemble of telescopes at the indicated spot among the guide stars. If the object was not seen in the 35 mm, as it usually was not, I would then look in the larger telescopes. If the object was not immediately visible even in the primary telescope – a not uncommon occur- rence due to inexact initial pointing – I would then scan around for it. -
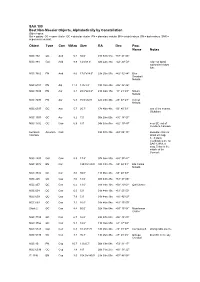
SAA 100 Best Non-Messier Objects, Alphabetically by Constellation
SAA 100 Best Non-Messier Objects, Alphabetically by Constellation Object types: Gal = galaxy OC = open cluster GC = globular cluster PN = planetary nebula BN = bright nebula DN = dark nebula SNR = supernova remnant Object Type Con VMag Size RA Dec Pop. Name Notes NGC 752 OC And 5.7 50.0' 01h 57m 51s +37° 41' 05" NGC 891 Gal And 9.9 14.0'x3.0' 02h 22m 36s +42° 20' 50" edge-on spiral w/prominent dust lane NGC 7662 PN And 8.6 17.0"x14.0" 23h 25m 57s +42° 32' 44" Blue Snowball Nebula NGC 6781 PN Aql 11.8 1.9'x1.8' 19h 18m 28s +06° 32' 46" NGC 7009 PN Aqr 8.3 28.0"x23.0" 21h 04m 15s -11° 21' 49" Saturn Nebula NGC 7293 PN Aqr 6.3 16.0'x12.0' 22h 29m 40s -20° 47' 23" Helical Nebula NGC 6397 GC Ara 5.7 25.7' 17h 40m 43s -53° 40' 33" one of the nearest Globulars NGC 1907 OC Aur 8.2 7.0' 05h 28m 00s +35° 18' 53" NGC 1502 OC Cam 6.9 8.0' 04h 07m 45s +62° 19' 49" near SE end of Kemble's Cascade Kemble's Asterism Cam 03h 57m 30s +63° 04' 13" Beautiful chain of Cascade about 20 mag. 5…9 stars; coordinates are for SAO 12969, a mag. 5 star in the middle of the Cascade NGC 2403 Gal Cam 8.5 17.8' 07h 36m 55s +65° 35' 42" NGC 3372 BN Car 120.0'x120.0' 10h 43m 47s -59° 52' 01" Eta Carina Nebula NGC 3532 OC Car 3.0 55.0' 11h 06m 23s -58° 40' 03" NGC 225 OC Cas 7.0 12.0' 00h 43m 28s +61° 47' 06" NGC 457 OC Cas 6.4 13.0' 01h 19m 10s +58° 20' 02" Owl Cluster NGC 654 OC Cas 6.5 5.0' 01h 44m 10s +61° 53' 00" NGC 659 OC Cas 7.9 5.0' 01h 44m 16s +60° 42' 00" NGC 663 OC Cas 7.1 16.0' 01h 46m 04s +61° 15' 00" Stock 2 OC Cas 4.4 60.0' 02h 15m 04s +59° 15' 58" Muscleman -

The Desert Sky Observer
Desert Sky Observer Volume 31 Antelope Valley Astronomy Club Newsletter January 2011 Up-Coming Events January 8: Star Party @ Vasquez Rocks January 14: Club Meeting* January 17: Board meeting @ Don’s house * Monthly meetings are held at the S.A.G.E. Planetarium on the Cactus School campus in Palmdale, the second Friday of each month. The meeting location is at the northeast corner of Avenue R and 20th Street East. Meetings start at 7 p.m. and are open to the public. Please note that food and drink are not allowed in the planetarium President Don Bryden Happy New Year! I hope this reaches you before the star party on the eighth. This is our Dark Sky Star Party for January and it’s going to be a joint effort with the Local Group – the Astro club from Santa Clarita. We have a unique opportunity to observe from Vasquez Rocks State Park – the site of many classic TV shows and movies – my personal favorite is “Arena”, the Star Trek episode featuring the Gorn. Maybe we can show up early and try to construct a bamboo and gunpowder cannon (though I’d just settle for finding some big diamonds lying around on the ground). There are many other great events planned for 2011 including the annual Messier Marathon, RTMC (over Memorial weekend this year!), and of course our summertime weekends at Mt. Pinos. I’m hoping to debut the club’s new 13” truss dob at the Messier Marathon as well. This scope, a former Coulter dobsonian that was donated to the club, has been refigured and transformed into a very portable, very easy to use visual scope.