DOCSLIB.ORG

The 9Th MATHEMATICAL CREATIVITY and GIFTEDNESS International Conference

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The 9Th MATHEMATICAL CREATIVITY and GIFTEDNESS International Conference The 9th MATHEMATICAL CREATIVITY AND GIFTEDNESS International 2015, June, 25 - 28 Conference PROCEEDINGS Editors: F l o r e n c e Mihaela Singer Florentina Toader Cristian Voica ISBN: 978-606-727-100-3 The 9th MATHEMATICAL CREATIVITY AND GIFTEDNESS International Conference PROCEEDINGS The International Group for Mathematical Creativity and Giftedness Sinaia, ROMANIA 2015 Table of contents WELLCOMING THE MCG-9 CONFERENCE................................................................................................................ 5 Florence Mihaela Singer, Roza Leikin MATHEMATICAL PATHOLOGIES AS PATHWAYS INTO CREATIVITY ......................................................................... 9 Bharath Sriraman PROFESSIONAL COMPETENCES OF TEACHERS AND ITS RELATION TO CREATIVITY ............................................... 10 Gabriele Kaiser MATHEMATICAL GIFTEDNESS GOES ONLINE: WHAT ARE THE NEW WAYS, TOOLS, RESOURCES TO DEVELOP TALENTS AND CREATIVITY IN STUDENTS? ............................................................................................................ 11 Viktor Freiman VIRTUAL CONVERSATIONS ON MATHEMATICAL TASKS ....................................................................................... 12 Rina Zazkis CONNECTION BETWEEN THEORY AND PRACTICE IN GIFTED EDUCATION ............................................................. 14 Roza Leikin, Florence Mihaela Singer, Linda Sheffield, Jong Sool Choi NURTURING STUDENTS’ CREATIVITY THROUGH TELLING MATHEMATICAL STORIES ............................................ 16 Anna Prusak SOLVING A MATHEMATICAL CREATIVITY TASK .................................................................................................... 22 Maria Kattou, Constantinos Christou, & Demetra Pitta-Pantazi THE PERCEPTION OF THE CONCEPT OF A “CHALLENGING TASK” BY MATHEMATICALLY PROMISING ELEMENTARY SCHOOL STUDENTS .............................................................................................................................................. 28 Mark Applebaum, Elena Gofman USING OPEN-ENDED PROBLEMS AND PROBLEM POSING ACTIVITIES IN ELEMENTARY MATHEMATICS CLASSROOM ........................................................................................................................................................ 34 Aleksandra Mihajlović, Mirko Dejić TH THE ANALYSIS OF 6 GRADE STUDENTS’ WORKS AT THE OPEN MATHEMATICAL OLYMPIAD ............................. 42 Ingrida Veilande, Sandra Krauze LEARNING MATH THROUGH RESEARCH AND COOPERATION ............................................................................... 48 Ariana-Stanca Văcărețu NOVELTIES IN MATH OLYMPIADS IN LATVIA ........................................................................................................ 54 Dace Kūma LE-MATH: LEARNING MATHEMATICS THROUGH NEW COMMUNICATION FACTORS ........................................... 60 Gregory Makrides and project Le-MATH partners PROBLEM SOLVING AND CHOICE-BASED PEDAGOGIES ........................................................................................ 68 Boris Koichu PROBLEM POSING COGNITIVE STYLE - CAN IT BE USED TO ASSESS MATHEMATICAL CREATIVITY? ...................... 74 Florence Mihaela Singer, Ildikó Pelczer, Cristian Voica The 9th International MCG Conference 2 Sinaia, Romania, 2015 CREATIVITY AND BISOCIATION ............................................................................................................................ 80 Bronislaw Czarnocha, William Baker SELF-CONTROL AND SELF-MONITORING PROCESSES OF GIFTED STUDENTS IN MATHEMATICAL PROBLEM SOLVING SITUATIONS .......................................................................................................................................... 86 Gönül Yazgan-Sağ, Ziya Argün COMBINATIONAL PLAY BETWEEN MATHEMATICAL DOMAINS AS ONE DIMENSION OF MATHEMATICAL CREATIVITY IN THE EARLY YEARS ......................................................................................................................... 94 Melanie Beck LOOKING FOR THE WAY TO SUPPORT CHILDREN’S MATHEMATICAL CREATIVITY .............................................. 100 Jana Slezakova, Ewa Swoboda IDENTIFYING MATHEMATICALLY GIFTED PRESCHOOLERS .................................................................................. 100 Panayiota Irakleous, Demetra Pitta-Pantazi MYTHS ABOUT “GIFTED” MATHEMATICS STUDENTS: HOW WIDESPREAD ARE THEY? ....................................... 114 Linda Jensen Sheffield MATHEMATICAL GIFTEDNESS AS DEVELOPING EXPERTISE................................................................................. 120 Torsten Fritzlar BAYBURT’S GOT GIFTED ..................................................................................................................................... 126 Zekeriya Karadag, Yasemin Devecioglu-Kaymakci CREATIVITY DEVELOPED WITHIN AN ACTIVITY THAT AFFORDS MULTIPLE SOLUTION AND MULTYMODAL ARGUMENTATION ............................................................................................................................................. 134 Naomi Prusak, Rina Hershkowitz “MATHE FÜR KLEINE ASSE” – AN ENRICHMENT PROJECT AT THE UNIVERSITY OF MÜNSTER ............................. 140 Ralf Benölken XCOLONY EDUCATIONAL ACTIVITIES ENHANCE SPATIAL REASONING IN MIDDLE SCHOOL STUDENTS .............. 146 Sorin Alexe, Gabriela Alexe, Consuela Voica, Cristian Voica ANALOGICAL-REASONING ABILITIES OF MATHEMATICALLY GIFTED CHILDREN - FIRST RESULTS OF THE VIDEO STUDY VISTAD ................................................................................................................................................... 154 Daniela Assmus, Frank Förster HIGHER ORDER THINKING IN MATHEMATICS .................................................................................................... 160 Paraskevi Sophocleous, Demetra Pitta-Pantazi EXAMINING COVERT IMPEDIMENTS TO INCLUSIVE EDUCATION FOR THE MATHEMATICALLY GIFTED LEARNERS IN SOUTH AFRICA ............................................................................................................................. 166 Michael Kainose Mhlolo “THE WEEK OF MATHEMATICS” – A PROJECT WITH CREATIVE APPROACHES .................................................... 172 Nicolae Popa A METHOD OF TEACHING MATHEMATICS IN KOREA SCIENCE ACADEMY ........................................................... 176 Choi Jong Sool PROSPECTIVE TEACHERS’ VIEWS OF CREATIVITY IN SCHOOL MATHEMATICS .................................................... 182 Elçin Emre-Akdoğan, Gönül Yazgan-Sağ The 9th International MCG Conference 3 Sinaia, Romania, 2015 ABILITY GROUPING FOR MATHEMATICALLY PROMISING STUDENTS ................................................................. 188 Sinan Kanbir SUPERMATH: A CREATIVE WAY TO ENGAGE TALENTED MATH STUDENTS ......................................................... 194 Edel M. Reilly DO TEACHER'S WAYS OF ENHANCING DISCOURSE IN HER CLASS LEAVE TRACES ON HER STUDENTS' POST-TEST RESPONSES? ...................................................................................................................................................... 206 Rina Hershkowitz, Michal Tabach, Shirly Azmon, Chris Rasmussen, Tommy Dreyfus ALGEBRAIC SYMBOLS AND CREATIVE THINKING ................................................................................................ 212 Michal Tabach, Alex Friedlander A STUDY ON THE RELATIONSHIP BETWEEN CREATIVE SCHOOL ENVIRONMENT AND CREATIVE STUDENTS` PERSONALITY, PROCESS AND PRODUCT ............................................................................................................ 212 Emilia Velikova MATHEMATICAL CREATIVITY AND THE AFFORDANCES OF DYNAMIC AND INTERACTIVE MATHEMATICS LEARNING ENVIRONMENTS ............................................................................................................................... 224 Zekeriya Karadag, Dragana Martinovic, Seyda Birni RATIONAL CREATIVITY: ALGORITHMS OR INNOVATION? TEACHING OPERATIONS WITH FRACTIONS ............... 231 Linda Jensen Sheffield EFFECTIVE FEEDBACK FOR EFFICIENT LEARNING: A COMPUTER-BASED SYSTEM OF ASSESSMENT ..................... 233 Florence Mihaela Singer, Cristian Voica VISUALIZING GEOMETRIC CONCEPTS USING A NOVEL TYPE OF 3D PUZZLES ...................................................... 235 Consuela Luiza Voica, Aurelia Grigorescu ACTIVITIES THAT ENGAGE GIFTED AND TALENTED STUDENTS IN PRODUCTIVE STRUGGLES WITH DESIRABLE DIFFICULTIES: A MODEL ENCOURAGING INTENSE DISCOURSE AND DEEP REASONING .................................... 237 William R. Speer USE OF ALGEBRAIC REASONING FOR EARLY IDENTIFICATION OF MATHEMATICAL TALENT ............................... 239 Sinan Kanbir THE NATURE OF CREATIVITY .............................................................................................................................. 242 Bronislaw Czarnocha, William Baker FOSTERING MATHEMATICAL GIFTEDNESS IN REGULAR CLASSROOM SETTING AND IN SPECIAL PROGRAMS ..... 244 Marianne Nolte The 9th International MCG Conference 4 Sinaia, Romania, 2015 WELLCOMING THE MCG-9 CONFERENCE Florence Mihaela Singer Roza Leikin Univ. of Ploiesti, Romania University of Haifa., Israel Chair - MCG-9 Conference President MCG Mathematical creativity and giftedness is a topic of increasing interest around the world. The International Group for Mathematical Creativity and Giftedness (MCG) brings together mathematics educators, mathematicians, researchers, and others who support the development of mathematical creativity and mathematical giftedness. The
Load more

Recommended publications
  • Prezentacja Programu Powerpoint
    PZLA GENERALNY SPONSOR POLSKIEGO ZWIĄZKU LEKKIEJ ATLETYKI I REPREZENTACJI POLSKI W LEKKIEJ ATLETYCE PZLA PZLA PZLA Polska z 12 medalami (7 złotych, 4 srebrne, 1 brązowy) zajęła drugie miejsce w tabeli medalowej. Pod względem ilości krążków zajęliśmy trzecie miejsca za gospodarzami oraz Brytyjczykami. Trzeci raz z rzędu biało-czerwoni przywożą z mistrzostw kontynentu 12. medali. PZLA ANITA WŁODARCZYK CZWARTY RAZ W KARIERZE ZOSTAŁA M ISTRZYNIĄ EUROPY W RZUCIE MŁOTEM. BRĄZOWY MEDAL ZDOBYŁA W BERLINIE JOANNA FIODOROW. NA DYSTANSIE 1500 METRÓW WICEMISTRZYNIĄ KONTYNENTU SOFIA ENNAOUI. Dla Anity Włodarczyk Berlin jest miastem wyjątkowym. Tutaj 9 lat temu tak naprawdę zaczęła się jej wielka kariera i lata niesamowitej dominacji w światowym rzucie młotem. Bieżący sezon nie jest jednak jej wymarzonym. Na szczęście mimo to Polka świetnie mobilizuje się na najważniejsze starty, chociaż – tak jak ten w niedzielny wieczór w Berlinie – zaczyna od bliższych prób. Konkurs na Olympiastadion otworzyła próbą poniżej 70 metrów. Kibice jednak mogli być spokojnie, że w kolejnych rzutach mistrzyni olimpijska będzie się regularnie poprawiać – tak jak przyzwyczaiła fanów. Tak było. W drugiej PZLA serii było 76.50, w trzeciej 77.82, w czwartej uzyskała najlepszą odległość dnia 78.94. Na koniec młot poleciał na 78.55. Włodarczyk zwyciężyła czwarty raz z rzędu, natomiast to jej piąty medal mistrzostw kontynentu. Swój medal Włodarczyk zadedykowała najwybitniejszej polskiej lekkoatletce, zmarłej 29 czerwca, Irenie Szewińskiej. Po czterech latach na trzeci stopień podium mistrzostw Europy powróciła Joanna Fiodorow. Zawodniczka Malwiny Sobierajskiej zaczęła konkurs podobnie jak Włodarczyk od rzutu na nieco ponad 69 metrów. Później rozkręciła się i w trzeciej uzyskała najlepszą odległość dnia, czyli 74.00.
    [Show full text]
  • Men's 200M Final 23.08.2020
    Men's 200m Final 23.08.2020 Start list 200m Time: 17:10 Records Lane Athlete Nat NR PB SB 1 Richard KILTY GBR 19.94 20.34 WR 19.19 Usain BOLT JAM Olympiastadion, Berlin 20.08.09 2 Mario BURKE BAR 19.97 20.08 20.78 AR 19.72 Pietro MENNEA ITA Ciudad de México 12.09.79 3 Felix SVENSSON SWE 20.30 20.73 20.80 NR 20.30 Johan WISSMAN SWE Stuttgart 23.09.07 WJR 19.93 Usain BOLT JAM Hamilton 11.04.04 4 Jan VELEBA CZE 20.46 20.64 20.64 MR 19.77 Michael JOHNSON USA 08.07.96 5 Silvan WICKI SUI 19.98 20.45 20.45 DLR 19.26 Yohan BLAKE JAM Boudewijnstadion, Bruxelles 16.09.11 6 Adam GEMILI GBR 19.94 19.97 20.56 SB 19.76 Noah LYLES USA Stade Louis II, Monaco 14.08.20 7 Bruno HORTELANO-ROIG ESP 20.04 20.04 8 Elijah HALL USA 19.32 20.11 20.69 2020 World Outdoor list 19.76 +0.7 Noah LYLES USA Stade Louis II, Monaco (MON) 14.08.20 19.80 +1.0 Kenneth BEDNAREK USA Montverde, FL (USA) 10.08.20 Medal Winners Stockholm previous 19.96 +1.0 Steven GARDINER BAH Clermont, FL (USA) 25.07.20 20.22 +0.8 Divine ODUDURU NGR Clermont, FL (USA) 25.07.20 2019 - IAAF World Ch. in Athletics Winners 20.23 +0.1 Clarence MUNYAI RSA Pretoria (RSA) 13.03.20 1. Noah LYLES (USA) 19.83 19 Aaron BROWN (CAN) 20.06 20.24 +0.8 André DE GRASSE CAN Clermont, FL (USA) 25.07.20 2.
    [Show full text]
  • FOCUS on the AUSTRIAN W UND ASSOCIATION the EWMA Journal ISSN Number: 1609-2759 Volume 12, No 1, January, 2012 EWMA
    Volume 12 Number 1 January 2012 Published by European Wound Management Association FOCUS ON THE AUSTRIAN W UND ASSOCIATION The EWMA Journal ISSN number: 1609-2759 Volume 12, No 1, January, 2012 EWMA Electronic Supplement January 2012 www.ewma.org Council The Journal of the European Jan Apelqvist Zena Moore Wound Management Association President Immediate Past President Published three times a year Editorial Board Sue Bale, UK, Editor Jan Apelqvist, Sweden Martin Koschnick, Germany Zena Moore, Ireland Marco Romanelli, Italy Rytis Rimdeika, Lithuania Corrado M. Durante Gerrolt Jukema Sue Bale Patricia Price José Verdú Soriano, Spain Treasurer Recorder Secretary Secretary Rita Gaspar Videira, Portugal Salla Seppänen, Finland EWMA web site www.ewma.org Editorial Office Paulo Alves Barbara E. Mark Collier Javorka Delic please contact: den Boogert-Ruimschotel EWMA Secretariat Nordre fasanvej 113 2000 Frederiksberg, Denmark. Tel: (+45) 7020 0305 Fax: (+45) 7020 0315 [email protected] Layout: Birgitte Clematide Luc Gryson Eskild Winther Henneberg Dubravko Huljev Nada Kecelj-Leskovec Martin Koschnick Sebastian Probst Printed by: CS Grafisk A/S, Denmark Copies printed: 11,000 Prices: The EWMA Journal is distributed in hard copies to members as part of their EWMA membership. Elia Ricci Rytis Rimdeika Salla Seppänen Robert Strohal José Verdú Soriano EWMA also shares the vision of an “open access” philosophy, which means that the journal is freely available online. CO-OPERATING ORGANISATIONS’ BOARD Individual subscription per issue: 7.50€ AFISCeP.be ICW SFFPC Libraries and institutions per issue: 25€ Christian Thyse, Christian Münter, Sylvie Meaume, Tommaso Bianchi, AISLeC Aleksandra Kuspelo, LBAA Christina Lindholm, SSIS The next issue will be published Roberto Cassino, AIUC Susan Knight, LUF Jozefa Košková, SSOOR in May 2012.
    [Show full text]
  • Men's 200M Final 04.09.2020
    Men's 200m Final 04.09.2020 Start list 200m Time: 20:42 Records Lane Athlete Nat NR PB SB 1 Marcus LAWLER IRL 20.30 20.40 20.95 WR 19.19 Usain BOLT JAM Olympiastadion, Berlin 20.08.09 2 Jiří POLÁK CZE 20.46 20.63 20.63 AR 19.72 Pietro MENNEA ITA Ciudad de México 12.09.79 3 Kojo MUSAH DEN 20.52 20.67 20.67 NR 20.19 Patrick STEVENS BEL Roma 05.06.96 WJR 19.93 Usain BOLT JAM Hamilton 11.04.04 4 Ján VOLKO SVK 20.24 20.24 20.74 MR 19.26 Yohan BLAKE JAM 16.09.11 5 Jonathan BORLÉE BEL 20.19 20.31 21.18 DLR 19.26 Yohan BLAKE JAM Boudewijnstadion, Bruxelles 16.09.11 6 Eseosa Fostine DESALU ITA 19.72 20.13 20.35 SB 19.76 Noah LYLES USA Stade Louis II, Monaco 14.08.20 7 Richard KILTY GBR 19.94 20.34 20.99 8 Julien WATRIN BEL 20.19 20.80 21.00 2020 World Outdoor list 19.76 +0.7 Noah LYLES USA Stade Louis II, Monaco (MON) 14.08.20 19.80 +1.0 Kenneth BEDNAREK USA Montverde, FL (USA) 10.08.20 Medal Winners Bruxelles previous 19.96 +1.0 Steven GARDINER BAH Clermont, FL (USA) 25.07.20 20.22 +0.8 Divine ODUDURU NGR Clermont, FL (USA) 25.07.20 2019 - IAAF World Ch. in Athletics Winners 20.23 +0.1 Clarence MUNYAI RSA Pretoria (RSA) 13.03.20 1. Noah LYLES (USA) 19.83 19 Noah LYLES (USA) 19.74 20.24 +0.8 André DE GRASSE CAN Clermont, FL (USA) 25.07.20 2.
    [Show full text]
  • RESULTS 100 Metres Women - Round 1
    Doha (QAT) 27 September - 6 October 2019 RESULTS 100 Metres Women - Round 1 First 3 in each heat (Q) and the next 6 fastest (q) advance to the Semi-Finals RECORDS RESULT NAME COUNTRY AGE VENUE DATE World Record WR 10.49 Florence GRIFFITH-JOYNER USA 29 Indianapolis (University Stadium), IN 16 Jul 1988 Championships Record CR 10.70 Marion JONES USA 24 Sevilla (La Cartuja) 22 Aug 1999 World Leading WL 10.73 Shelly-Ann FRASER-PRYCE JAM 33 Kingston (JAM) 21 Jun 2019 World Leading WL 10.73 Elaine THOMPSON JAM 27 Kingston (JAM) 21 Jun 2019 Area Record AR National Record NR Personal Best PB Season Best SB 28 September 2019 16:30 START TIME 25° C 67 % m/s Heat 1 TEMPERATURE HUMIDITY -0.2 6 WIND PLACE NAME COUNTRY DATE of BIRTH LANE RESULT REACTION Fn 1 Shelly-Ann FRASER-PRYCE JAM 27 Dec 86 8 10.80 Q 0.173 2 Murielle AHOURÉ CIV 23 Aug 87 6 11.05 Q SB 0.180 3 Gina LÜCKENKEMPER GER 21 Nov 96 9 11.29 (.282) Q 0.235 4 Ewa SWOBODA POL 26 Jul 97 2 11.29 (.285) q 0.185 5 Diana VAISMAN ISR 23 Jul 98 4 11.39 0.144 6 Tebogo MAMATHU RSA 27 May 95 7 11.42 0.143 7 Andrea PURICA VEN 21 Nov 95 5 11.96 0.154 8 Sarswati CHAUDHARY NEP 12 Feb 97 3 12.72 NR 0.152 28 September 2019 16:37 START TIME 25° C 67 % m/s Heat 2 TEMPERATURE HUMIDITY -0.3 6 WIND PLACE NAME COUNTRY DATE of BIRTH LANE RESULT REACTION Fn 1 Marie-Josée TA LOU CIV 18 Nov 88 3 10.85 Q PB 0.192 2 Daryll NEITA GBR 29 Aug 96 7 11.12 Q PB 0.156 3 Tatjana PINTO GER 2 Jul 92 9 11.19 Q 0.152 4 Yongli WEI CHN 11 Oct 91 6 11.28 (.275) q 0.173 5 Crystal EMMANUEL CAN 27 Nov 91 4 11.30 (.298) q 0.161 6 Marije
    [Show full text]
  • June 9 2021 Board of Directors Regular Meeting Agenda Packet V2
    EAST CONTRA COSTA FIRE PROTECTION DISTRICT BOARD OF DIRECTORS Adam Langro Carrie Nash Brian Oftedal Stephen Smith Joe Young Vice President President AGENDA Board of Directors Regular Meeting Due to COVID-19, this meeting will be conducted via teleconference only (no physical location) pursuant to the Governor's Executive OrdersN-25-20 & N-29-20. Directors, staff and the public may participate remotely. Call In Number: 1(872) 240-3212 Access Code: 490-316-781 https://global.gotomeeting.com/join/490316781 Wednesday, June 9, 2021 6:30 PM Members of the public are encouraged to attend remotely at the phone number or website listed above. Directions for providing public comment via teleconference will be provided at the beginning of the meeting. Public comments submitted to [email protected] prior to the meeting will be summarized during the meeting and posted online at: https://eccfpd.specialdistrict.org/2021-06-09-eccfpd-board-of-directors-meeting Upon request, the District provides for written agenda materials in appropriate alternative formats or other disability-related modification or accommodation to enable individuals with disabilities to participate in and provide comments related to public meetings. Please submit a request, including your name, phone number and/or email address, and a description of the modification, accommodation, auxiliary aid, service or alternative format requested at least two days before the meeting. Requests should be emailed to [email protected], or submitted by phone at (925) 634-3400. Requests made by mail (sent to Regina Rubier, 150 City Park Way, Brentwood, CA 94513) must be received at least two days before the meeting.
    [Show full text]
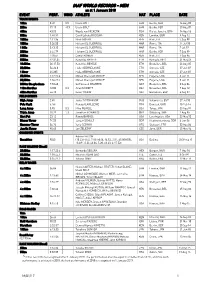
  • IAAF WORLD RECORDS - MEN As at 1 January 2018 EVENT PERF
    IAAF WORLD RECORDS - MEN as at 1 January 2018 EVENT PERF. WIND ATHLETE NAT PLACE DATE TRACK EVENTS 100m 9.58 0.9 Usain BOLT JAM Berlin, GER 16 Aug 09 200m 19.19 -0.3 Usain BOLT JAM Berlin, GER 20 Aug 09 400m 43.03 Wayde van NIEKERK RSA Rio de Janeiro, BRA 14 Aug 16 800m 1:40.91 David Lekuta RUDISHA KEN London, GBR 9 Aug 12 1000m 2:11.96 Noah NGENY KEN Rieti, ITA 5 Sep 99 1500m 3:26.00 Hicham EL GUERROUJ MAR Roma, ITA 14 Jul 98 1 Mile 3:43.13 Hicham EL GUERROUJ MAR Roma, ITA 7 Jul 99 2000m 4:44.79 Hicham EL GUERROUJ MAR Berlin, GER 7 Sep 99 3000m 7:20.67 Daniel KOMEN KEN Rieti, ITA 1 Sep 96 5000m 12:37.35 Kenenisa BEKELE ETH Hengelo, NED 31 May 04 10,000m 26:17.53 Kenenisa BEKELE ETH Bruxelles, BEL 26 Aug 05 20,000m 56:26.0 Haile GEBRSELASSIE ETH Ostrava, CZE 27 Jun 07 1 Hour 21,285 Haile GEBRSELASSIE ETH Ostrava, CZE 27 Jun 07 25,000m 1:12:25.4 Moses Cheruiyot MOSOP KEN Eugene, USA 3 Jun 11 30,000m 1:26:47.4 Moses Cheruiyot MOSOP KEN Eugene, USA 3 Jun 11 3000m Steeplechase 7:53.63 Saif Saaeed SHAHEEN QAT Bruxelles, BEL 3 Sep 04 110m Hurdles 12.80 0.3 Aries MERRITT USA Bruxelles, BEL 7 Sep 12 400m Hurdles 46.78 Kevin YOUNG USA Barcelona, ESP 6 Aug 92 FIELD EVENTS High Jump 2.45 Javier SOTOMAYOR CUB Salamanca, ESP 27 Jul 93 Pole Vault 6.16i Renaud LAVILLENIE FRA Donetsk, UKR 15 Feb 14 Long Jump 8.95 0.3 Mike POWELL USA Tokyo, JPN 30 Aug 91 Triple Jump 18.29 1.3 Jonathan EDWARDS GBR Göteborg, SWE 7 Aug 95 Shot Put 23.12 Randy BARNES USA Los Angeles, USA 20 May 90 Discus Throw 74.08 Jürgen SCHULT GDR Neubrandenburg, GDR 6 Jun 86 Hammer Throw
    [Show full text]
  • Młodzieżowe Rekordy Polski
    stan na: 22.08.2019 MŁODZIE ŻOWE REKORDY POLSKI (U-23) MĘŻ CZY ŹNI 100 m 10.17 Dariusz KU Ć 240486 AZS-AWF Kraków 27.05.2006 Biała Podlaska +1.3 200 m 20.31 Marcin J ĘDRUSI ŃSKI 280981 Olimpia Pozna ń 09.08.2002 Monachium -0.5 400 m 45.35 Marek PLAWGO 250281 KS Warszawianka Warszawa 22.06.2002 Annecy 800 m 1:43.30 Adam KSZCZOT 020989 RKS Łód ź 20.09.2011 Rieti 1000 m 2:16.99 Adam KSZCZOT 020989 RKS Łód ź 31.05.2011 Ostrawa 1500 m 3:36.37 Michał ROZMYS 130395 UKS Barnim Goleniów 05.06.2017 Praga 3000 m 7:50.42 Michał BARTOSZAK 210670 Olimpia Pozna ń 12.09.92 Nuoro 5000m 13:29.72 Michał BARTOSZAK 210670 Olimpia Pozna ń 03.06.92 Victoria 10.000 m 28:30.4 Bronisław MALINOWSKI 040651 Olimpia Grudzi ądz 04.08.73 Celje 3000 m z przeszkodami 8:17.32 Radosław POPŁAWSKI 160183 Astra Nowa Sól 24.08.2004 Ateny 100 m przez płotki 13.29 Tomasz ŚCIGACZEWSKI 181178 KS Warszawianka Warszawa 30.06.99 Oslo +1.5 13.29 Artur NOGA 020588 KS Warszawianka Warszawa 03.07.2010 Eugene +1.6 400 m przez płotki 48.16 Marek PLAWGO 250281 Niestowarzyszony. 12.05.2001 Osaka Skok wzwy ż 2.36 Aleksander WALERIA ŃCZYK 010982 Wawel Kraków 20.07.2003 Bydgoszcz Skok o tyczce 5.91 Paweł WOJCIECHOWSKI 060689 SL WKS Zawisza Bydgoszcz 15.08.2011 Szczecin Skok w dal 8.21 Marcin STARZAK 211085 AZS-AWF Kraków 04.07.2007 Salamanka +1.4 Trójskok 17.11 Jacek PASTUSI ŃSKI 080964 Resovia Rzeszów 17.06.86 Warszawa +1.1 Pchni ęcie kul ą 22.00 h Konrad BUKOWIECKI 170397 KS AZS UWM Olsztyn 15.02.2018 Toru ń Rzut dyskiem 64.74 Piotr MAŁACHOWSKI 070683 WKS Śląsk Wrocław 26.06.2005 Biała Podlaska
    [Show full text]
  • Teachers of Refugees: a Review of the Literature
    By Emily Richardson with Leonora MacEwen and Ruth Naylor Teachers of refugees: a review of the literature TEACHERS OF REFUGEES: A REVIEW OF THE LITERATURE Teachers of refugees: a review of the literature Education Development Trust Highbridge House, 16–18 Duke Street, Reading, Berkshire RG1 4RU T +44 (0) 118 902 1000 E [email protected] W www.educationdevelopmenttrust.com 1 TEACHERS OF REFUGEES: A REVIEW OF THE LITERATURE © COPYRIGHT EDUCATION DEVELOPMENT TRUST 2018. THE VIEWS AND OPINIONS EXPRESSED IN THIS PUBLICATION ARE THOSE OF THE AUTHORS AND DO NOT NECESSARILY REPRESENT THE VIEWS OF EDUCATION DEVELOPMENT TRUST. ISBN 978-1-909437-95-1 2 TEACHERS OF REFUGEES: A REVIEW OF THE LITERATURE Contents Welcome to Education Development Trust 4 Chapter 6: Teacher preparation and 44 professional development About the International Institute for 4 Education Planning (IIEP)-UNESCO Formal training 47 About the authors 5 Non-formal training 48 Acknowledgements 5 Research gaps on teacher preparation 53 and development Acronyms and abbreviations 7 Chapter 7: Teacher remuneration 54 Chapter 1: Introduction 8 and incentives Methodology and scope 10 Funding teachers of refugees 57 Limitations 11 Research gaps on teacher remuneration 59 and incentives Chapter 2: Education of refugees: 14 overview, history and the importance Chapter 8: Teacher retention 60 of education Factors affecting retention other than 61 remuneration Chapter 3: The right to education for 18 Research gaps on teacher retention 63 refugees: frameworks and policies
    [Show full text]
  • ARIA Licensors
    ARIA Licensors Licensing Copyright Owners BMG AUSTRALIA LIMITED 194 Miller Street, North Sydney NSW 2060 COLOSSAL RECORDS OF AUSTRALIA PTY LTD 14-16 Wilson Avenue, Brunswick VIC 3056 EMI MUSIC (AUSTRALIA) PTY LTD 98-100 Glover Street, Cremorne NSW 2090 * FESTIVAL RECORDS PTY LTD 235 Pyrmont Street, Pyrmont NSW 2009 * MUSHROOM DISTRIBUTION SERVICES PTY LTD 55 Danks Street, Port Melbourne VIC 3207 JANDA RECORDS (AUST) PTY LTD 2/17 Tennyson Road, Mortlake NSW 2137 LARRIKIN ENTERTAINMENT PTY LTD 235 Pyrmont Street, Pyrmont NSW 2009 SHOCK RECORDS PTY LTD 200 Beavers Road, Northcote VIC 3070 SONY MUSIC ENTERTAINMENT (AUSTRALIA) LTD 11 Hargrave Street, East Sydney NSW 2010 UNIVERSAL MUSIC AUSTRALIA LIMITED 3 Munn Reserve, Millers Point NSW 2000 WARNER MUSIC AUSTRALIA PTY LTD 39-47 Albany Street, Crows Nest NSW 2065 * Trading as Festival Mushroom Records Please note that the following sound recordings are expressly excluded from this Agreement: AC/DC: and EMI Music owned or controlled sound recordings by the Beatles (and solo members), Queen (and solo members) and Rolling Stones (and solo members). ARIA Labels Licensing Copyright Owner Labels 1500 Records (Universal) Alligator (Shock) 415 Records (Sony) Almo Sounds (Universal) 4AD (Shock) Alternative Tentacles (Shock) 4TH & Broadway (Universal) Amadeo (Universal) 510 Records (Universal) Ambient Sound (Shock) 550 Music (Sony) American Clave (Shock) A Star Academy (Zomba) American Decca Jazz (Universal) A&E Records Ltd (FMR) American Explorer (Warner) A&M (Universal) Anchor & Hope (Shock) A&M Records
    [Show full text]
  • 2018 European Championships Statistics – Women’S 100M by K Ken Nakamura
    2018 European Championships Statistics – Women’s 100m by K Ken Nakamura Summary Page All time performance list at the European Championships Performance Performer Time Wind Name Nat Pos Venue Yea 1 1 10.73 2.0 Christine Arron FRA 1 Budape st 1998 2 10.81 1.3 Christine Arron 1sf1 Budapest 1998 3 2 10.83 2.0 Irina Privalova RUS 2 Budapest 1998 4 3 10.87 2.0 Ekaterini Thanou GRE 3 Budapest 1998 5 4 10.89 1.8 Katrin Krabbe GDR 1 Split 1990 6 5 10.90 -0.2 Dafne Schippers NED 1 Amsterdam 2016 7 6 10.91 0.8 Marlies Göhr GDR 1 Stuttgart 1986 Margin of Victory Difference Winning time Wind Name (winner) Nat Venue Year Max 0.30 10.90 -0.2 Dafne Schippers NED Amsterdam 2016 Min 0.01 11.10 0.6 Verena Sailer GER Barcelona 2010 Best Marks for Places in the European Championships Pos Time Wind Name Nat Venue Year 1 10.73 2.0 Christine Arron FRA Budapest 1998 2 10.83 2.0 Irina Privalova RUS Budapest 1998 3 10.87 2.0 Ekaterini Thanou GRE Budapest 1998 4 10.92 2.0 Zhanna Pintusevich-Block UKR Budapest 1998 Fastest non-qualifier for the final Time Wind Position Name Nat Venue Year 11.21 1.3 5sf1 Oksana Ekk RUS Budapest 1998 Multiple Gold Medalists: Marlies Göhr (GDR): 1978, 1982, 1986 Dafne Schippers (NED) 2014, 2016 Multiple Medals by athletes from a single nation Nation Year Gold Silver Bronze FRA 2010 Veronique Mang Myriam Soumare RUS 2006 Yekaterina Grigoryeva Irina Khabarova GDR 1990 Katrin Krabbe Silke Gladisch-Möller Kerstin Behrendt GDR 1982 Marlies Göhr Barbel Wöckel FRG 1971 Ingrid Mickler-Becker Elfgard Schittenhelm POL 1966 Klobukowska Irena Szewinska
    [Show full text]
  • TSG 18 Proceedings.Pdf
    14th International Congress on Mathematical Education July 11-18, 2021, Shanghai Proceedings of the ICME-14 Topic Study Group 18 Students’ identity, motivation, and attitude towards mathematics and its study Maike Vollstedt (Ed.) TSG 18. Students’ identity, motivation, and attitude towards mathematics and its study Chair: Maike Vollstedt University of Bremen, Germany [email protected] Co-chair: Masitah Shahrill Universiti Brunei Darussalam [email protected] Team members: Bozena Maj-Tatsis University of Rzeszow [email protected] Karin Brodie Wits University [email protected] Donglin Chen Faculty of Education, The University of Hong Kong [email protected] IPC Liaison person: Ewa Swoboda University of Rzeszow 2021, Shanghai, China: ICME-14 2 SESSION 1 (p. 7-45) 14:30-16:30 BEIJING TIME, JULY 13TH CHAIR: MAIKE VOLLSTEDT 14:30-14:40 Maike VOLLSTEDT, Masitah Shahrill, Bozena Maj-Tatsis, Karin Brodie, Donglin Chen Opening Session 14:40-15:00 Kai Kow Joseph YEO 200: MATHEMATICS-ANXIETY STUDENTS REASONS AND FEELINGS WHEN CHOOSING TO SOLVE PARTICULAR PROBLEMS 15:00-15:10 Katrina Grace Q. Sumagit & Nympha B. Joaquin 400: Mathematical Problem-Solving Beliefs of Filipino Seventh Graders 15:10-15:20 Masitah Shahrill, Ai Len Gan, Haryani Haji Mohammad 1946: UNDERSTANDING THE INTENTIONS OF SHADOW EDUCATION IN BRUNEI DARUSSALAM 15:20-15:30 Changgen PEI & Jiancheng FAN 709: DEVELOPING AND VALIDATING A SCALE FOR MEASURING STUDENTS' CRITICAL THINKING DISPOSITION IN MATHEMATICS EDUCATION 15:30-15:40 Beijia TAN, Jenee Love,
    [Show full text]