DOCSLIB.ORG

Fatigue Overview Introduction to Fatigue Analysis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Fatigue Overview Introduction to Fatigue Analysis Fatigue overview Introduction to fatigue analysis • Fatigue is the failure of a component after several repetitive load cycles. • As a one-time occurrence, the load is not dangerous in itself. Over time the alternating load is able to break the structure anyway. • It is estimated that between 50 and 90 % of product failures is caused by fatigue, and based on this fact, fatigue evaluation should be a part of all product development. What is fatigue? In materials science, fatigue is the progressive and localized structural damage that occurs when a material is subjected to cyclic loading (material is stressed repeatedly). Clients tous différents Routes de qualités variables Contraintes Fatigue Design in Automotive Industry Conception fiable PSA (Peugeot Citroën) Résistances 3s 3s Dispersion matériau Dispersion de production Fatigue • Fracture mechanics can be divided into three stages: 1. Crack nucleation 2. Crack-growth 3. Ultimate ductile failure Introduction to fatigue analysis • Fatigue is the failure of a component after several repetitive load cycles. • As a one-time occurrence, the load is not dangerous in itself. Over time the alternating load is able to break the structure anyway. • It is estimated that between 50 and 90 % of product failures is caused by fatigue, and based on this fact, fatigue evaluation should be a part of all product development. Historical background • In comparison to the classical stress analysis, fatigue theory is a relative new phenomenon. The need to understand fatigue arose after the industrial revolution introduced steel structures. Three areas were particularly involved in early failures: Railway trains, Mining equipment and Bridges. Historical background • 1837: Wilhelm Albert publishes the first article on fatigue. He devised a test machine for conveyor chains used in the Clausthal mines. • 1839: Jean-Victor Poncelet describes metals as being tired in his lectures at the military school at Metz. • 1870: Wöhler summarizes his work on railroad axles. He concludes that cyclic stress range is more important than peak stress and introduces the concept of endurance limit. • 1910: O. H. Basquin proposes a log-log relationship for SN curves, using Wöhler's test data. • 1945: A. M. Miner popularizes A. Palmgren's (1924) linear damage hypothesis as a practical design tool. • 1954: L. F. Coffin and S. S. Manson explain fatigue crack-growth in terms of plastic strain in the tip of cracks. • 1968: Tatsuo Endo and M. Matsuiski devise the rainflow-counting algorithm and enable the reliable application of Miner's rule to random loadings. Historical background • Fatigue theory is basically empirical. This means that the process of initiation of micro cracks that finally will form macroscopic cracks in the material is not accounted for in detail in the equations. • Fatigue properties must be treated by statistical means due to large variation during testing. • Virtually all mathematical equations dealing with fatigue are fitted to test results coming from materials testing. Fields of application & analysis considerations • Whenever a structure is subjected to time varying loads, fatigue must be taken into account. Typical structures subjected to time varying loads are for example: – Rotating machinery (pumps, turbines, fans, shafts) – Pressure vessel equipment (vessels, pipes, valves) – Land based vehicles, ships, air- and space crafts – Bridges, lifting equipment, offshore structures Fields of application & analysis considerations • In the design specification of the part there are some questions that must be answered, for example: 1. What is the expected number of cycles during the expected life time? 2. Shall the individual components be designed for infinite life or a specified life? 3. In case of a specified life time, what service/inspection intervals are needed? Fields of application & analysis considerations • Common Decisions for Fatigue Analysis • There are 5 common input decision topics upon which your fatigue results are dependent. These fatigue decisions are grouped into the types listed below: 1. Fatigue Analysis Type 2. Loading Type 3. Mean Stress Effects 4. Multi-axial Stress Correction 5. Fatigue Modification Factor Loading types When minimum and maximum stress levels are constant, this is referred to as constant amplitude loading. This is a much more simple case and will be discussed first. Otherwise, the loading is known as variable amplitude or non- constant amplitude and requires special treatment Loading types The loading may be proportional or non- proportional: - Proportional loading means that the ratio of the principal stresses is constant, and the principal stress axes do not change over time. This essentially means that the response with an increase or reversal of load can easily be calculated. - Conversely, non-proportional loading means that there is no implied relationship between the stress components. Typical cases include the following: Alternating between two different load cases, An alternating load superimposed on a static load , Nonlinear boundary conditions . Terminology Consider the case of constant amplitude, proportional loading, with min and max stress values σmin and σmax: The stress range Δσ is defined as (σmax- σmin) The mean stress σm is defined as (σmax+ σmin)/2 The stress amplitude or alternating stress σa is Δσ/2 The stress ratio R is σmin/σmax Fully-reversed loading occurs when an equal and opposite load is applied. This is a case of σm = 0 and R = -1. Zero-based loading occurs when a load is applied and removed. This is a case of σm = σmax/2 and R = 0. Stress life theory • General: – The stress life (SN) analysis estimates the time spent to initiate and grow a crack until the component breaks into parts. – The model takes the stress variation and makes a look-up in a material graph to find the corresponding number of cycles to failure. – Historically this is the first mathematical model developed for lifetime calculations, and the one with the most readily available material data. – The analysis requires stress results from a linear static analysis as input. • Suitability and limitations: – The method is applicable for components failing after more than 10.000 to 100.000 cycles (HCF). – For higher loadings with a shorter fatigue lifetime local plasticity is probably considerable not only at the crack tip, but locally on the structure as well. – Such cases should be analysed using the Strain Life Method instead as the stress life method gives overly conservative results here. Stress life theory Material data – When doing test on stress range versus fatigue life and plotting the results on two logarithmic axis, the results tends to be linear. – Gustaw Wöhler observed this when doing bending test on railroad shafts, illustrated below. – Later Basquin formulated this mathematically in a power law. The curve may consist of several linear pieces. Two parameters for each of the curves in Basquin's law are needed as input: Starting point S and slope b. s The properties are usually found for zero mean stress and a uniaxial stress state on polished specimens. Stress life theory • Metals typically experience infinite fatigue life for low stress ranges. • This is modelled as a flat curve at a cut-off stress ΔSe and above Ne cycles. • Ne is usually between 1 and 5 million cycles and Se is typically half the ultimate strength Rm. The plateau tendency may not be present for other metals, such as aluminium or stainless steel. • As explained, Basquin is not valid in the low cycle fatigue region, so caution should be used if the calcu- lated life is low – as illustrated with the dashed line in the figure below. Stress life theory • The material curve on previous page may describe the fatigue strength of a base material, but it may also be describing the fatigue strength of a whole component, such as a welded T-joint. • Alternatively the material curve to be used may be dictated by a design standard, based not only on the material but also as a function of geometry, failure consequences and inspection intervals for example. Stress life theory Basquin's law Basquin's law calculates the number of cycles to fracture as: Nf = ƒ (S, S0, N0, b) Nf = Number of cycles to failure S = Applied stress range = Δσ = 2σa (N0, S0) = Point on the material curve b = Fatigue strength exponent (Slope of material curve) Basquin's law is usually presented as: However, usually So = Se and No = Ne, thus making Basquin's law: Stress life theory Basquin’s law In lack of fatigue material data, the following guidelines can be used (although other methods exist to predict this): 6 Se=0.5×Su at Ne = 10 3 S =0.9×Su at N = 10 Su = Rm (ultimate tensile stress) Stress life theory Mean stress correction Since the fatigue properties given are valid for zero mean stress only, one must do corrections if mean stresses are not equal to zero in the actual load history. Compressive mean stresses are good for fatigue life, while mean tensile stresses are bad. The three load histories to the right all have equal stress amplitudes, but different mean stresses. As such they will experience different fatigue life also. This is not covered by Basquin’s formulae. We will now look at a method to account for this so that Basquin still can be used. Stress life theory Mean stress correction A number of models exist to compensate for mean stresses, four are incorporated in ANSYS Fatigue module. - Goodman (England 1899) - Soderberg (USA 1930) - Gerber (Germany 1870) - Mean Stress Curves The three first models work in the same manner: The stress amplitude that is to be used in Basquin’s law is corrected according to the mean stress σm and yield or tensile stress σy or σu. The three models are shown graphically below: Stress life theory Mean stress correction The last model does not use any correction formulae, but instead have several material curves input - each corresponding to its own Stress Ratio (R): Tests yield results between that predicted by the Goodman and Gerber models.
Load more

Recommended publications
  • Top Performance When the Going Gets Tough
    Top performance when the going gets tough The Alfa Laval DuroShell plate-and-shell heat exchanger Sub-headline coming soon DuroShell – plate-and-shell made tougher Alfa Laval DuroShell is a specially engineered plate-and-shell heat exchanger ideal for demanding duties and corrosive media. Able to withstand fatigue even at high temperatures and pressures, it outperforms not only traditional heat exchangers, but also other plate-and-shells. As flexible as it is strong DuroShell creates new possibilities through its com- pactness, efficiency and exceptional resistance to fatigue. Able to work with liquids, gases and two- phase mixtures, it stands out among heat exchangers in its duty range. DuroShell handles pressures up to 100 barg (1450 psig) in compliance with PED and ASME, and temperatures as high as 450 °C (842 °F). Built for your application DuroShell is fully welded and gasket-free, with internal features that make it still more robust. Plates are avail- able in 316L stainless steel, while the pressure vessel itself can be built in 316L stainless steel or carbon steel. Three different sizes are possible, with heat transfer surfaces ranging 2–235 m2 (21.5–2530 ft 2) in area. DuroShell RollerCoaster Robust and efficient performance. DuroShell PowerPack Optimized flow distribution and fatigue resistance. Learn more at www.alfalaval.com/duroshell Plate-and-shell benefits made better • More uptime and longer life due to • Installation savings through even greater fatigue resistance more compact, lightweight design • Higher operating pressures thanks • Greater reliability as a result of to robust, patented construction closed, fully welded construction • Operational gains created by 15–20 % higher thermal efficiency How it works Revolutionary technology Optimized flow DuroShell is a plate-and-shell heat exchanger, but one DuroShell operates with one media on the plate side with a unique internal design.
    [Show full text]
  • Corrosion Fatigue of Austenitic Stainless Steels for Nuclear Power Engineering
    metals Article Corrosion Fatigue of Austenitic Stainless Steels for Nuclear Power Engineering Irena Vlˇcková 1,*, Petr Jonšta 2, ZdenˇekJonšta 2, Petra Vá ˇnová 2 and Tat’ána Kulová 2 1 RMTSC, Material & Metallurgical Research Ltd., Remote Site Ostrava, VÚHŽ a.s., Dobrá 739 51, Czech Republic 2 Department of Materials Engineering, VŠB-Technical University of Ostrava, Ostrava 708 33, Czech Republic; [email protected] (P.J.); [email protected] (Z.J.); [email protected] (P.V.); [email protected] (T.K.) * Correspondence: [email protected]; Tel.: +420-558601257 Academic Editor: Hugo F. Lopez Received: 21 September 2016; Accepted: 8 December 2016; Published: 16 December 2016 Abstract: Significant structural steels for nuclear power engineering are chromium-nickel austenitic stainless steels. The presented paper evaluates the kinetics of the fatigue crack growth of AISI 304L and AISI 316L stainless steels in air and in corrosive environments of 3.5% aqueous NaCl solution after the application of solution annealing, stabilizing annealing, and sensitization annealing. Comparisons were made between the fatigue crack growth rate after each heat treatment regime, and a comparison between the fatigue crack growth rate in both types of steels was made. For individual heat treatment regimes, the possibility of the development of intergranular corrosion was also considered. Evaluations resulted in very favourable corrosion fatigue characteristics of the 316L steel. After application of solution and stabilizing annealing at a comparable DK level, the fatigue crack growth rate was about one half compared to 304L steel. After sensitization annealing of 316L steel, compared to stabilizing annealing, the increase of crack growth rate during corrosion fatigue was slightly higher.
    [Show full text]
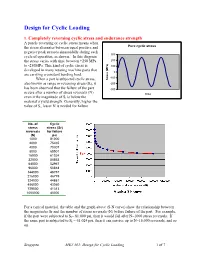
  • Design for Cyclic Loading, Soderberg, Goodman and Modified Goodman's Equation
    Design for Cyclic Loading 1. Completely reversing cyclic stress and endurance strength A purely reversing or cyclic stress means when the stress alternates between equal positive and Pure cyclic stress negative peak stresses sinusoidally during each 300 cycle of operation, as shown. In this diagram the stress varies with time between +250 MPa 200 to -250MPa. This kind of cyclic stress is 100 developed in many rotating machine parts that 0 are carrying a constant bending load. -100 When a part is subjected cyclic stress, Stress (MPa) also known as range or reversing stress (Sr), it -200 has been observed that the failure of the part -300 occurs after a number of stress reversals (N) time even it the magnitude of Sr is below the material’s yield strength. Generally, higher the value of Sr, lesser N is needed for failure. No. of Cyclic stress stress (Sr) reversals for failure (N) psi 1000 81000 2000 75465 4000 70307 8000 65501 16000 61024 32000 56853 64000 52967 96000 50818 144000 48757 216000 46779 324000 44881 486000 43060 729000 41313 1000000 40000 For a typical material, the table and the graph above (S-N curve) show the relationship between the magnitudes Sr and the number of stress reversals (N) before failure of the part. For example, if the part were subjected to Sr= 81,000 psi, then it would fail after N=1000 stress reversals. If the same part is subjected to Sr = 61,024 psi, then it can survive up to N=16,000 reversals, and so on. Sengupta MET 301: Design for Cyclic Loading 1 of 7 It has been observed that for most of engineering materials, the rate of reduction of Sr becomes negligible near the vicinity of N = 106 and the slope of the S-N curve becomes more or less horizontal.
    [Show full text]
  • Very High Cycle Fatigue of Engineering Materials
    Faculty of Technology and Science Materials Engineering Vitaliy Kazymyrovych Very high cycle fatigue of engineering materials (A literature review) Karlstad University Studies 2009:22 Vitaliy Kazymyrovych Very high cycle fatigue of engineering materials (A literature review) Karlstad University Studies 2009:22 Vitaliy Kazymyrovych. Very high cycle fatigue of engineering materials - A literature review Research Report Karlstad University Studies 2009:22 ISSN 1403-8099 ISBN 978-91-7063-246-4 © The Author Distribution: Faculty of Technology and Science Materials Engineering SE-651 88 Karlstad +46 54 700 10 00 www.kau.se Printed at: Universitetstryckeriet, Karlstad 2009 Very high cycle fatigue of engineering materials (A literature review) V.Kazymyrovych* Department of Materials Engineering, Karlstad University SE-651 88, Sweden * Email address: [email protected] Abstract This paper examines the development and present status of the Very High Cycle Fatigue (VHCF) phenomenon in engineering materials. The concept of ultrasonic fatigue testing is described in light of its historical appearance covering the main principles and equipment variations. The VHCF behaviour of the most important materials used for very long life applications is presented, with particular attention paid to steels. In section 3 the VHCF properties of titanium-, nickel-, aluminium- and magnesium alloys are described. Furthermore, the typical fatigue behaviour and mechanisms of pure metals are presented. Section 4 examines the VHCF properties of various types of steels e.g. low carbon steel, spring steel, stainless steel, bearing steel as well as tool steel. In addition to this, the main material defects that initiate VHCF failure are examined in this study. Furthermore, the different stages characteristic for fatigue crack development in VHCF are described in section 5 in terms of relative importance and sequence.
    [Show full text]
  • Creep-Fatigue Failure Diagnosis
    Review Creep-Fatigue Failure Diagnosis Stuart Holdsworth Received: 22 October 2015 ; Accepted: 6 November 2015 ; Published: 16 November 2015 Academic Editor: Robert Lancaster EMPA: Swiss Federal Laboratories for Materials Science and Technology Überlandstrasse 129, Dübendorf CH-8600, Switzerland; [email protected]; Tel.: +41-58-765-47-32 Abstract: Failure diagnosis invariably involves consideration of both associated material condition and the results of a mechanical analysis of prior operating history. This Review focuses on these aspects with particular reference to creep-fatigue failure diagnosis. Creep-fatigue cracking can be due to a spectrum of loading conditions ranging from pure cyclic to mainly steady loading with infrequent off-load transients. These require a range of mechanical analysis approaches, a number of which are reviewed. The microstructural information revealing material condition can vary with alloy class. In practice, the detail of the consequent cracking mechanism(s) can be camouflaged by oxidation at high temperatures, although the presence of oxide on fracture surfaces can be used to date events leading to failure. Routine laboratory specimen post-test examination is strongly recommended to characterise the detail of deformation and damage accumulation under known and well-controlled loading conditions to improve the effectiveness and efficiency of failure diagnosis. Keywords: failure diagnosis; creep-fatigue; material condition; mechanical analysis 1. Introduction The diagnosis of failures invariably involves consideration of both the associated material condition and the results of a mechanical analysis of prior operating history. Material condition refers not only to a knowledge of the chemical composition and mechanical properties relative to those originally specified for the failed component, but also the appearance and extent of microstructural and physical damage responsible for failure.
    [Show full text]
  • Creep, Fatigue and Creep-Fatigue Interactions in Modified 9% Cr - 1% Mo (P91) Steels" (2013)
    University of Arkansas, Fayetteville ScholarWorks@UARK Theses and Dissertations 5-2013 Creep, Fatigue and Creep-Fatigue Interactions in Modified 9% rC - 1% Mo (P91) Steels Valliappa Kalyanasundaram University of Arkansas, Fayetteville Follow this and additional works at: http://scholarworks.uark.edu/etd Part of the Mechanics of Materials Commons, Structural Engineering Commons, and the Structural Materials Commons Recommended Citation Kalyanasundaram, Valliappa, "Creep, Fatigue and Creep-Fatigue Interactions in Modified 9% Cr - 1% Mo (P91) Steels" (2013). Theses and Dissertations. 692. http://scholarworks.uark.edu/etd/692 This Dissertation is brought to you for free and open access by ScholarWorks@UARK. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of ScholarWorks@UARK. For more information, please contact [email protected], [email protected]. CREEP, FATIGUE AND CREEP-FATIGUE INTERACTIONS IN MODIFIED 9% Cr – 1% Mo (P91) STEELS CREEP, FATIGUE AND CREEP-FATIGUE INTERACTIONS IN MODIFIED 9% Cr – 1% Mo (P91) STEELS A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Mechanical Engineering By Valliappa Kalyanasundaram Madurai Kamaraj University Bachelor of Engineering in Mechanical Engineering, 2004 University of Arkansas Master of Science in Mechanical Engineering, 2008 May 2013 University of Arkansas ABSTRACT Grade P91 steel, from the class of advanced high-chrome ferritic steels, is one of the preferred materials for many elevated temperature structural components. Creep-fatigue (C-F) interactions, along with oxidation, can accelerate the kinetics of damage accumulation and consequently reduce such components’ life. Hence, reliable C-F test data is required for meticulous consideration of C-F interactions and oxidation, which in turn is vital for sound design practices.
    [Show full text]
  • Analysis of Fatigue and Wear Behaviour in Ultrafine Grained Connecting Rods
    metals Article Analysis of Fatigue and Wear Behaviour in Ultrafine Grained Connecting Rods Rodrigo Luri, Carmelo J. Luis, Javier León, Juan P. Fuertes, Daniel Salcedo and Ignacio Puertas * Mechanical, Energetics and Materials Engineering Department, Public University of Navarre, Campus Arrosadía s/n, Pamplona 31006, Spain; [email protected] (R.L.); [email protected] (C.J.L.); [email protected] (J.L.); [email protected] (J.P.F.); [email protected] (D.S.) * Correspondence: [email protected]; Tel.: +34-948-169-305 Received: 3 July 2017; Accepted: 20 July 2017; Published: 29 July 2017 Abstract: Over the last few years there has been an increasing interest in the study and development of processes that make it possible to obtain ultra-fine grained materials. Although there exists a large number of published works related to the improvement of the mechanical properties in these materials, there are only a few studies that analyse their in-service behaviour (fatigue and wear). In order to bridge the gap, in this present work, the fatigue and wear results obtained for connecting rods manufactured by using two different aluminium alloys (AA5754 and AA5083) previously deformed by severe plastic deformation (SPD), using Equal Channel Angular Pressing (ECAP), in order to obtain the ultrafine grain size in the processed materials are shown. For both aluminium alloys, two initial states were studied: annealed and ECAPed. The connecting rods were manufactured from the previously processed materials by using isothermal forging. Fatigue and wear experiments were carried out in order to characterize the in-service behaviour of the components.
    [Show full text]
  • Assessment of Fatigue Damage and Crack Propagation in Ceramic Matrix Composites by Infrared Thermography
    ceramics Article Assessment of Fatigue Damage and Crack Propagation in Ceramic Matrix Composites by Infrared Thermography Konstantinos G. Dassios * and Theodore E. Matikas Department of Materials Science &Engineering, University of Ioannina, 45110 Ioannina, Greece; [email protected] * Correspondence: [email protected] Received: 20 March 2019; Accepted: 27 May 2019; Published: 10 June 2019 Abstract: The initiation and propagation of damage in SiC fiber-reinforced ceramic matrix composites under static and fatigue loads were assessed by infrared thermography (IRT). The proposed thermographic technique, operating in lock-in mode, enabled early prediction of the residual life of composites, and proved vital in the rapid determination of the materials’ fatigue limit requiring testing of a single specimen only. IRT was also utilized for quantification of crack growth in the materials under cyclic loads. The paper highlights the accuracy and versatility of IRT as a state-of-the art damage assessment tool for ceramic composites. Keywords: ceramics; composites; thermography; fatigue; crack growth 1. Introduction The highly desirable properties of ceramic matrix composites (CMC), including damage tolerance, fracture toughness, wear- and corrosion resistance, and crack growth resistance, allow them to withstand severe thermomechanical loading conditions [1]. As such, the materials are used today in aerospace applications, such as braking systems, structural components, nozzles, and thermal barriers. Glass–ceramic matrix composites reinforced with continuous SiC fibers have received particular scientific attention as they offer additional attractive properties, such as high strength and stiffness, low density, and chemical inertness at conventional and oxidative environments and over a wide range of temperatures [2]. The necessity of monitoring the structural integrity of aerospace composites and their structures is key to the prevention of failure as well as to the safe and economical operation of the structures.
    [Show full text]
  • Investigation of Corrosion Fatigue Phenomena in Transient Zone of Mechanical Drive Steam Turbines and Its Preventive Measures
    Proceedings of the Second Middle East Turbomachinery Symposium 17 – 20 March 2013, Doha, Qatar Investigation of Corrosion Fatigue Phenomena in Transient Zone of Mechanical Drive Steam Turbines and its Preventive Measures by Satoshi Hata Engineering and Design Division Mitsubishi Heavy Industries, Compressor Corporation Naoyuki Nagai Hiroshima Research & Development Center Mitsubishi Heavy Industries, Ltd. Norihito Fujimura MCO Saudi Arabia, LCC. (MCOSA) Mitsubishi Heavy Industries, Compressor Corporation Satoshi Hata ABSTRACT Satoshi Hata is a Group Manager For mechanical drive steam turbines, the investigation within the Turbo Machinery results of corrosion fatigue phenomena in the transient zone Engineering Department, Mitsubishi are introduced, including basic phenomena on expansion Heavy Industries, Ltd., in Hiroshima, line and actual design and damage experience. These results Japan. He has 30 year experience in were analyzed from the standpoint of stress intensity during R&D for nuclear uranium centrifuges, turbomolecular pumps, heavy-duty the start of cracking. In order to resolve such problems, gas turbines, steam turbines and preventive coating and blade design methods against fouling compressors. Mr. Hata has B.S., M.S. and corrosive environments are developed. Detailed and Ph.D. degrees (in Mechanical evaluation test results are given for coating performance Engineering) from Kyusyu Institute of using a unique test procedure simulating fouling phenomena Technology. and washing conditions. Finally, the results of the Naoyuki
    [Show full text]
  • Creep-Fatigue Deformation Behaviour of OFHC-Copper and Cucrzr Alloy with Different Heat Treatments and with and Without Neutron Irradiation
    Risø-R-1528(EN) Creep-Fatigue Deformation Behaviour of OFHC-Copper and CuCrZr Alloy with Different Heat Treatments and with and without Neutron Irradiation B.N. Singh, M. Li, J.F. Stubbins and B.S. Johansen Risø National Laboratory Roskilde Denmark August 2005 Author: B.N. Singh1), M. Li2), J.F. Stubbins3) and B.S. Johansen1) Risø-R-1528(EN) August 2005 Title: Creep-Fatigue Deformation Behaviour of OFHC-Copper and CuCrZr Alloy with Different Heat Treatments and with and without Neutron Irradiation Department: Materials Research Department 1)Materials Research Department, Risø National Laboratory DK-4000 Roskilde, Denmark 2)Metals and Ceramics Division, Oak Ridge National Laboratory Oak Ridge, Tennessee, USA 3)Department of Nuclear, Plasma and Radiological Engineering University of Illinois, Urbana, Illinois, USA ISSN 0106-2840 Abstract ISBN 87-550-3465-9 The creep-fatigue interaction behaviour of a precipitation hardened CuCrZr alloy was investigated at 295 and 573 K. To determine the effect of irradiation a number of fatigue specimens were irradiated at 333 and 573 K to a dose level in the range of 0.2 - 0.3 dpa and were tested at room temperature and 573 K, respectively. The creep-fatigue deformation behaviour of OFHC-copper was also investigated but only in the Contract no.: unirradiated condition and at room temperature. The creep-fatigue TW1-TVV-COP, TW2-TVM-CUCFA and interaction was simulated by applying a certain holdtime on both tension TW3-TVM-CUCFA2 and compression sides of the cyclic loading with a frequency of 0.5 Hz. Holdtimes of up to 1000 seconds were used.
    [Show full text]
  • Study on Wear and Fatigue Performance of Two Types of High-Speed Railway Wheel Materials at Different Ambient Temperatures
    materials Article Study on Wear and Fatigue Performance of Two Types of High-Speed Railway Wheel Materials at Different Ambient Temperatures Lei MA 1,* , Wenjian WANG 2, Jun GUO 2 and Qiyue LIU 2 1 School of Mechanical Engineering, Xihua University, Chengdu 610039, China 2 Tribology Research Institute, State Key Laboratory of Traction Power, Southwest Jiao Tong University, Chengdu 610031, China; [email protected] (W.W.); [email protected] (J.G.); [email protected] (Q.L.) * Correspondence: [email protected] Received: 14 January 2020; Accepted: 2 March 2020; Published: 5 March 2020 Abstract: The wear and fatigue behaviors of two newly developed types of high-speed railway wheel materials (named D1 and D2) were studied using the WR-1 wheel/rail rolling–sliding wear simulation device at high temperature (50 C), room temperature (20 C), and low temperature ( 30 C). The ◦ ◦ − ◦ results showed that wear loss, surface hardening, and fatigue damage of the wheel and rail materials at high temperature (50 C) and low temperature ( 30 C) were greater than at room temperature, ◦ − ◦ showing the highest values at low temperature. With high Si and V content refining the pearlite lamellar spacing, D2 presented better resistance to wear and fatigue than D1. Generally, D2 wheel material appears more suitable for high-speed railway wheels. Keywords: alpine region; high-speed wheel and rail materials; temperature; wear; fatigue damage 1. Introduction Railways play a vital role in the development of rail transportation. The environmental climate has a certain impact on wheel/rail systems exposed to the open air. Especially in China, wheel and rail materials may serve under extreme temperature conditions due to torridity and severe cold.
    [Show full text]
  • Bahx Product Bulletin
    BAHX PRODUCT BULLETIN Issue 2 - January 2021 BAHX PRODUCT BULLETIN TABLE OF CONTENTS INTRODUCTION .......................................................3 CO2 ICE FORMATION ............................................. 12 Who should read this What it is and why it’s bad What this bulletin covers What can cause it OPERATION ..............................................................5 How to detect it Lifespan How to prevent it End of life How to fix it Principles of operation EXCESSIVE THERMAL GRADIENTS .................. 13 PLUGGING ................................................................7 What they are and why they’re bad What it is and why it’s bad What can cause them What can cause it How to detect them How to detect it How to prevent them How to prevent it How to fix them How to fix it OTHER HAZARDS TO BAHX ................................ 15 FOULING ....................................................................8 INSPECTING OPERATING DATA ......................... 15 What it is and why it’s bad BAHX ASSESSMENT ............................................. 16 What can cause it While out of service How to detect it Visual inspection How to prevent it External How to fix it Internal CHEMICAL ATTACK .................................................9 Pressure test What it is and why it’s bad Leak test What can cause it During operation How to detect it Visual inspection How to prevent it Fluid composition testing How to fix it Monitor operating data ICE FORMATION .................................................... 10 IN CONCLUSION .................................................... 18 What it is and why it’s bad Other BAHX Resources What can cause it CONTACT US .......................................................... 19 How to detect it How to prevent it How to fix it HYDRATE ACCUMULATION ................................. 11 What it is and why it’s bad What can cause it How to detect it How to prevent it How to fix it © 2021 Chart Energy & Chemicals, Inc.
    [Show full text]