ABSTRACT KAPOOR, ASHISH. Fiber-Based
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Fall ’17 Footwear Trends Smart Textiles Tech Advances Trade Show Previews & Recaps Making It in America
TEXTILE INSIGHT Trends In Apparel & Footwear Design and Innovation • January/February 2017 iNvEnToLoGy HOW THE TEXTILE INDUSTRY IS INVENTING ITS FUTURE Fall ’17 Footwear Trends Smart Textiles Tech Advances Trade Show Previews & Recaps Making it in America A FORMULA4 MEDIA PUBLICATION TEXTILEINSIGHT.COM A breakthrough fiber innovation you have to feel to believe. Eastman Avra performance fibers wick better, dry faster, and keep you at your coolest and most comfortable. AVRAfromEastman.com ©2017 Eastman Chemical Company. Eastman brands referenced herein are trademarks of Eastman Chemical Company or one of its subsidiaries. The ® used on Eastman brands denotes registered trademark status in the U.S.; marks may also be registered internationally. JANUARY/FEBRUARY 2017 JANUARY/FEBRUARY Executive Editor Mark Sullivan [email protected] 646-319-7878 Editor /Associate Publisher Emily Walzer [email protected] Managing Editor Cara Griffin Art Director Francis Klaess Associate Art Director Mary McGann Contributing Editors Suzanne Blecher Kurt Gray Jennifer Ernst Beaudry Kathlyn Swantko Publisher Jeff Nott [email protected] 516-305-4711 Advertising Jeff Gruenhut [email protected] 404-467-9980 Christina Henderson 516-305-4710 [email protected] Troy Leonard [email protected] 352-624-1561 Katie O’Donohue [email protected] 828-244-3043 Sam Selvaggio [email protected] 212-398-5021 Production Brandon Christie 516 305-4710 [email protected] Business Manager Marianna Rukhvarger 516-305-4709 [email protected] Biosteel is the latest knit upper shoe technology from Adidas set to debut this year. Subscriptions store.formula4media.com Formula4 Media Publications 6 / In the Market 40 / Made in America Sports Insight The New Year begins with trade show previews, reports on Before “Think locally, act globally” became a popular buzz- Outdoor Insight Footwear Insight Performance Days, advances in digital textiles printing, and phrase, IDEAL Fastener was putting the strategy to work. -

To Be Published in Gazette of India, Extra Ordinary, Part 1, Section1
To be published in Gazette of India, Extra ordinary, Part 1, Section1 F. No. 15/16/2013-DGAD Government of India Ministry of Commerce & Industry Department of Commerce (Directorate General of Anti Dumping & Allied Duties) 4th Floor, Jeevan Tara Building, 5, Parliament Street, New Delhi 110001 Dated the 23rd March, 2015 NOTIFICATION (Final Findings) Subject: Final Findings in the sunset review of anti-dumping duty imposed on the imports of Acrylic Fibre originating in or exported from Korea RP and Thailand-reg. A. BACKGROUND OF THE CASE 1. No. 15/16/2013-DGAD:- Whereas having regard to the Customs Tariff Act, 1975 as amended from time to time (herein after referred to as the Act) and the Customs Tariff (Identification, Assessment and Collection of Duty on Dumped Articles and for Determination of Injury) Rules, 1995 (herein after referred to as the AD Rules), the Designated Authority (herein after referred to as the Authority), initiated the original anti dumping investigation in respect of the imports of Acrylic Fibre (hereinafter referred to as the subject goods) originating in or exported from USA, Thailand and Korea RP on 13.9.1996 and definitive anti dumping duty was recommended vide Final Findings Notification No. 47/ADD/1W dated 14.10.1997. The Central Government had imposed the anti dumping duty. The sunset review of the anti dumping duty so imposed against USA, Thailand and Korea RP was initiated by the Authority vide Notification No. 26/1/2001-DGAD dated 07.08.2001 and the Final Findings were issued vide Notification No. 26/1/2001-DGAD dated 06.08.2002. -

U.S. EPA, Pesticide Product Label, CUTTER INSECT REPELLENT
U.S. ENVIRONMENTAL PROTECTION AGENCY EPA Reg. Date of Issuance: Office of Pesticide Programs Number: Registration Division (H750SC) 401 "M" St., S.W. 121-91 Washington, D.C. 20460 OCT 2 a 2005 Term of Issuance: NOTICE OF PESTICIDE: Conditional _x__ Registration Reregistration Name of Pesticide Product: (under FIFRA. as amended) CUTTER Insect Repellent 15KP Name and Address of Registrant (include ZIP Code): Spectrum Division of United Industries P.O. Box 142642 St. Louis, MO 63114-0642 Note: Changes in labeling differing in substance from that accepted in connection with this registration must be submitted to and accepted by the Registration Division prior to use of the label in commerce. In any correspondence on this product always refer to the above EPA registration number. On the basis of information furnished by the registrant, the above named pesticide is hereby registered/reregistered under the Federal Insecticide, Fungicide and Rodenticide Act. Registration is in no way to be construed as an endorsement or recommendation of this product by the Agency. In order to protect health and the environment, the Administrator, on his motion, may at any time suspend or cancel the registration of a pesticide in accordance with the Act. The acceptance of any name in connection with the registration of a product under this Act is not to be construed as giving the registrant a right to exclusive use of the name or to its use if it has been covered by others. This product is conditionally registered in accordance with FIFRA sec. 3(c) (7) (A) provided that you: 1. -
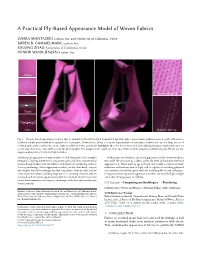
A Practical Ply-Based Appearance Model of Woven Fabrics
A Practical Ply-Based Appearance Model of Woven Fabrics ZAHRA MONTAZERI, Luxion, Inc. and University of California, Irvine SØREN B. GAMMELMARK, Luxion, Inc. SHUANG ZHAO, University of California, Irvine HENRIK WANN JENSEN, Luxion, Inc. Photo Ours Frontlit close-up Photo Ours Backlit close-up Fig. 1. Our ply-based appearance model is able to simulate both reflected and transmitted light through complex weave patterns as seen on the left andour rendered results match with photographs of a real sample. Furthermore, it has a compact representation that makes it efficient to use for large pieces of clothing such as the scarf shown on the right. In addition to the anisotropic highlights, the color due to front and back lighting changes considerably and our model reproduces the color shift seen in the photographs. The images on the right are close-ups of the scarf showing the individual yarns. Pleaseseethe supplementary video for the full light rotation. Simulating the appearance of woven fabrics is challenging due to the complex In this paper, we introduce a practical appearance model for woven fabrics. interplay of lighting between the constituent yarns and fibers. Conventional We model the structure of a fabric at the ply level and simulate the local surface-based models lack the fidelity and details for producing realistic appearance of fibers making up each ply. Our model accounts for both close-up renderings. Micro-appearance models, on the other hand, can pro- reflection and transmission of light and is capable of matching physical duce highly detailed renderings by depicting fabrics fiber-by-fiber, but be- measurements better than prior methods including fiber based techniques. -

Textile Design: a Suggested Program Guide
DOCUMENT RESUME CI 003 141 ED 102 409 95 Program Guide.Fashion TITLE Textile Design: A Suggested Industry Series No. 3. Fashion Inst. of Tech.,New York, N.T. INSTITUTION Education SPONS AGENCY Bureau of Adult,Vocational, and Technictl (DREW /OE), Washington,D.C. PUB DATE 73 in Fashion Industry NOTE 121p.; For other documents Series, see CB 003139-142 and CB 003 621 Printing AVAILABLE FROM Superintendent of Documents,U.S. Government Office, Washington, D.C.20402 EDRS PRICE NP -$0.76 HC-$5.70 PLUS POSTAGE Behavioral Objectives; DESCRIPTORS Adult, Vocational Education; Career Ladders; *CurriculumGuides; *Design; Design Crafts; EducationalEquipment; Employment Opportunities; InstructionalMaterials; *Job Training; Needle Trades;*Occupational Rome Economics; OccupationalInformation; Program Development; ResourceGuides; Resource Units; Secondary Education;Skill Development;*Textiles Instruction IDENTIFIERS *Fashion Industry ABSTRACT The textile designguide is the third of aseries of resource guidesencompassing the various five interrelated program guide is disensions of the fashionindustry. The job-preparatory conceived to provide youthand adults withintensive preparation for and also with careeradvancement initial entry esploysent jobs within the textile opportunities withinspecific categories of provides an overviewof the textiledesign field, industry. The guide required of workers. It occupational opportunities,and cospetencies contains outlines of areasof instruction whichinclude objectives to suggestions for learning be achieved,teaching -

Mussels As a Model System for Integrative Ecomechanics
UC Santa Barbara UC Santa Barbara Previously Published Works Title Mussels as a model system for integrative ecomechanics. Permalink https://escholarship.org/uc/item/0xr832ct Journal Annual review of marine science, 7(1) ISSN 1941-1405 Authors Carrington, Emily Waite, J Herbert Sarà, Gianluca et al. Publication Date 2015 DOI 10.1146/annurev-marine-010213-135049 Peer reviewed eScholarship.org Powered by the California Digital Library University of California MA07CH19-Carrington ARI 20 November 2014 8:4 Mussels as a Model System for Integrative Ecomechanics Emily Carrington,1 J. Herbert Waite,2 Gianluca Sara,` 3 and Kenneth P. Sebens1 1Department of Biology and Friday Harbor Laboratories, University of Washington, Friday Harbor, Washington 98250; email: [email protected], [email protected] 2Department of Molecular, Cellular, and Developmental Biology, University of California, Santa Barbara, California 93106; email: [email protected] 3Dipartimento di Scienze della Terra e del Mare, University of Palermo, 90128 Palermo, Italy; email: [email protected] Annu. Rev. Mar. Sci. 2015. 7:443–69 Keywords First published online as a Review in Advance on byssus, dislodgment, dynamic energy budget, fitness, mussel foot proteins, August 25, 2014 tenacity The Annual Review of Marine Science is online at marine.annualreviews.org Abstract This article’s doi: Mussels form dense aggregations that dominate temperate rocky shores, and 10.1146/annurev-marine-010213-135049 they are key aquaculture species worldwide. Coastal environments are dy- Copyright c 2015 by Annual Reviews. Annu. Rev. Marine. Sci. 2015.7:443-469. Downloaded from www.annualreviews.org namic across a broad range of spatial and temporal scales, and their changing All rights reserved abiotic conditions affect mussel populations in a variety of ways, including Access provided by University of California - Santa Barbara on 01/30/15. -

Cyromazine) During Woolscouring and Its Effects on the Aquatic Environment the Fate of Vetrazin® (Cyromazine) During
Lincoln University Digital Thesis Copyright Statement The digital copy of this thesis is protected by the Copyright Act 1994 (New Zealand). This thesis may be consulted by you, provided you comply with the provisions of the Act and the following conditions of use: you will use the copy only for the purposes of research or private study you will recognise the author's right to be identified as the author of the thesis and due acknowledgement will be made to the author where appropriate you will obtain the author's permission before publishing any material from the thesis. THE FATE OF VETRAZIN@ (CYROMAZINE) DURING WOOLSCOURING AND ITS EFFECTS ON THE AQUATIC ENVIRONMENT THE FATE OF VETRAZIN® (CYROMAZINE) DURING WOOLSCOURING AND ITS EFFECTS ON THE AQUATIC ENVIRONMENT A thesis submitted in fulfilment of the requirements for the degree of DOCTOR OF PHILOSOPHY in AQUATIC TOXICOLOGY at LINCOLN UNIVERSITY P.W. Robinson 1995 " ; " i Abstract of a thesis submitted in partial fulfllment of the requirement for the Degree of Doctor of Philosophy THE FATE OF VETRAZIN® (CYROMAZINE) DURING WOOLSCOURING AND ITS EFFECTS ON THE AQUATIC ENVIRONMENT by P.W. Robinson A number of ectoparasiticides are used on sheep to protect the animals from ill health associated with infestations of lice and the effects of fly-strike. Most of the compounds currently in use are organophosphate- or pyrethroid-based and have been used for 15-20 years, or more. In more recent times, as with other pest control strategies, there has been a tendency to introduce 'newer' pesticides, principally in the form of insect growth regulators (IGRs). -

Proceedings Transformation in a Changing Climate
PROCEEDINGS in a changing climate International Conference in Oslo 19 - 21 June 2013 2013 University of Oslo Department of Sociology and Human Geography P.O. box 1096 Blindern 0317 OSLO Norway Date: 12.12.13 ISBN: 978-82-570-2001-9 Citation: University of Oslo (2013) Proceedings of Transformation in a Changing Climate, 19-21 June 2013, Oslo, Norway. University of Oslo. Interactive IPCC co-sponsorship does not imply IPCC endorsement or approval of these proceedings or any recommendations or conclusions contained herein. Neither the papers presented at the Conference nor the report of its proceedings have been subjected to IPCC review. Conference webpage: WWW.ISS.UIO.NO/TRANSFORMATION Table of contents 04 THE FIRST “TRANSFORMATION IN A CHANGING CLIMATE” CONFERENCE: INTRODUCTION AND REFLECTIONS 07 CONFERENCE OPENING SPEECH 08 CONFERENCE WELCOME SPEECH 10 PROGRAM AT A GLANCE: Tuesday • Wednesday • Thursday • Friday 14 CONFERENCE COMMITTEES 15 LIST OF SPONSORS ARTICLES 16 Responding to climate change: The three spheres of transformation 24 Triggering transformation: Managing resilience or invoking real change? 33 Distilling the characteristics of transformational change in a changing climate 43 Transition management as an approach to deal with climate change 53 When is change change? What can we learn regarding societal transformation in the face of climate change from the previous work of local authorities on promoting sustainable development? 62 Institutional transformation in a devolved governance system: Possibilities and limits 72 Post -

World Economic Survey 1962
WORLD ECONOMIC SURVEY 1962 II. Current Economie Developments UNITED NATIONS Department of Economic and Social Affairs WOR D ECO OMIC SURVEY 1962 II. Current Economic Developments UNITED NATIONS New York, 1963 E/3761/Rev.l ST/ECA/78 UNITED NATIONS PUBLICATION Sales No.: 63. II.C. 2 Price: $U.5. 1.50 (or equivalent in other currencies) FOREWORD This report represents part II of the World Economic Survey, 1962. As indicated in the Foreword to part I, "The Developing Countries in World Trade" (Sales No.: 63.II.C.1), it consists of three chapters dealing with recent developments in the world economy. Chapter 1 analyses the situation in the industrially advanced private enterprise countries. Chapter 2 reviews current trends in the countries that are heavily dependent on the export of primary commodities. Chapter 3 provides an account of recent changes in the centrally planned economies. The three chapters follow a brief introduction which draws attention to some of the salient features of the current situation. Most of the analysis is concerned with the calendar year 1962; chapters 1 and 2 conclude with brief assessments of the outlook for 1963. These discussions of outlook draw to a large extent on the replies of Governments to a questionnaire on economic trends, problems and policies circulated by the Secretary-General in November 1962. Like part I, part II of the World Economic Survey, 1962 was prepared in the Department of Economic and Social Affairs by the Bureau of General Economic Research and Policies. iii EXPLANATORY NOTES The following -

Teachers' Handbook
-- TTeeaacchheerrss’’ HHaannddbbooookk (Based on learning outcomes) CLASS-VII SSCCIIEENNCCEE FOREWORD CLASSES VI TO VIII SUBJECT – SCIENCE This document is prepared with a notion to enable the teachers to ascertain learning skills accurately in the subject of science for classes VI to VIII so that the minimum level of learning (MLL) may be attained by the children and their periodic assessment can be done to maintain the record of their progress. ABOUT THE DOCUMENT • The document includes Learning Outcomes prepared by NCERT distinctively for classes VI, VII and VIII in Science and learners achievement sheet for the assessment of learners. • It covers the full syllabus for each class and gives an insight into the progress made in each class by the students. • The material in the documents can be used as an assessment tool for classes VI to VIII in the subject of science and it is meant both for teachers and the students. • The document provides the crux of the Learning Outcomes and efforts are made to avoid direct information, definition and description, and instead an opportunity is provided to the children to correlate experience and explore the environment in its surroundings. • This document reaches the desired Learning Outcomes targeting the competencies through multiple choice and open ended questions to access the learning levels of the students in each class. • The language in the document is simple for the childrento read and understand and the Progress sheet has been given to record the growth of every student by the teacher. • In spite of the fact that all efforts are made to give full freedom to the child to explore but there might have been some discrepancies. -

Accord (BLMCC) Instruction and Reference Guide
INTRODUCTION INTRODUCTION Thank you for purchasing this machine. Before using this machine, carefully read the “IMPORTANT SAFETY INSTRUCTIONS”, and then study this manual for the correct operation of the various functions. In addition, after you have finished reading this manual, store it where it can quickly be accessed for future reference. IMPORTANT SAFETY INSTRUCTIONS Please read these safety instructions before attempting to use the machine. DANGER - To reduce the risk of electrical shock 1 Always unplug the machine from the electrical outlet immediately after using, when cleaning, making any user servicing adjustments mentioned in this manual, or if you are leaving the machine unattended. WARNING - To reduce the risk of burns, fire, electrical shock, or injury to persons. 2 Always unplug the machine from the electrical outlet when making any adjustments mentioned in the instruction manual. • To unplug the machine, switch the machine to the symbol “O” position to turn it off, then grasp the plug and pull it out of the electrical outlet. Do not pull on the cord. • Plug the machine directly into the electrical outlet. Do not use an extension cord. • Always unplug your machine if there is a power failure. 3 Electrical Hazards: • This machine should be connected to an AC power source within the range indicated on the rating label. Do not connect it to a DC power source or converter. If you are not sure what kind of power source you have, contact a qualified electrician. • This machine is approved for use in the country of purchase only. 4 Never operate this machine if it has a damaged cord or plug, if it is not working properly, has been dropped or damaged, or water is spilled on the unit. -

Chapter 5 Basic Embroidery
Cover1-4 C M Y K XF9969-1011 Chapter 5 Basic Embroidery BEFORE EMBROIDERING ..................................... 196 COMBINING PATTERNS .......................................238 Embroidery Step by Step ........................................................196 Editing Combined Patterns ..................................................... 238 Attaching Embroidery Foot “W+” with LED pointer ..............197 ■ Selecting combined embroidery patterns................................240 Attaching the Embroidery Unit ..............................................197 Sewing Combined Patterns..................................................... 241 ■ About the Embroidery Unit .................................................... 197 PREPARING THE FABRIC.......................................242 ■ Removing the Embroidery Unit ............................................. 198 SELECTING PATTERNS.......................................... 200 Attaching Iron-on Stabilizers (Backing) to the Fabric ............ 242 Hooping the Fabric in the Embroidery Frame ........................ 243 ■ Copyright Information ........................................................... 200 ■ Types of Embroidery Frames ..................................................243 ■ Pattern Selection Screens ...................................................... 201 ■ Inserting the Fabric.................................................................244 Selecting Embroidery Patterns/Decorative Alphabet Patterns/ ■ Using the Embroidery Sheet ...................................................245