Pr08a81l1ta' a P3dal1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

WPT World Championship: Kidpoker Mit Denkwürdiger Hand Ausgeschieden
WPT World Championship: KidPoker mit denkwürdiger Hand ausgeschieden Der dritte Turniertag der WPT World Championsip im Bellagio von Las Vegas hatte es in sich. 188 Spieler waren an die Tische in der Fontana Lounge zurückgekehrt und es ging zunächst darum, die 100 bezahlten Plätze zu erreichen, um sich ein Stück vom insgesamt $ 13.216.250 großen Preispool zu sichern. Das hielt die Spieler allerdings nicht davon ab, von Beginn an viel zu riskieren. In den ersten beiden Levels schrumpfte das Feld auf 132 zusammen und zu den Ausgeschiedenen gehörten unter anderem Dario Minieri, Hevad Khan, Humberto Brenes und Barry Greenstein vom Team PokerStars Pro sowie Doyle Brunson, Dan Harrington, Mike Matusow, Dave Ulliott, Scotty Nguyen, Barny Boatman, Kathy Liebert und später auch der letzte deutsche Spieler Andreas Krause. Daniel Negreanu, der mit 154.600 Chips in den Tag gestartet war, erlebte ein unglaubliches Auf und Ab. Den Großteil seines Stacks büßte er mit Pocketqueens ein, nachdem die Chips vor dem Flop in die Mitte wanderten und sein Gegner im Showdown [King of clubs] [King of hearts] umdrehte. 35.000 blieben dem Team-PokerStars-Pro noch, doch er schaffte es tatsächlich, diesen Stapel im weiteren Verlauf wieder auf 200.000 aufzubauen und die Moneybubble sicher zu überstehen. Die letztlich entscheidende Hand wird dem Kanadier aber noch lange in Erinnerung bleiben. Gleich vier Spieler sahen den Flop mit [Ten of hearts] [Nine of diamonds] [Four of hearts] und Brian Rast feuerte 65.000 in die Mitte. Beeindrucken konnte er seine Gegner damit aber nicht, im Gegenteil: Negreanu ging mit 189.000 all-in, gefolgt von Dino French mit 195.000 und Saifuddin Ahmad mit ungefähr 290.000 in Chips. -

Staff, Visiting Scientists and Graduate Students 2011
Staff, Visiting Scientists and Graduate Students at the Pescara Center December 2011 2 Contents ICRANet Faculty Staff……………………………………………………………………. p. 17 Adjunct Professors of the Faculty .……………………………………………………… p. 35 Lecturers…………………………………………………………………………………… p. 72 Research Scientists ……………………………………………………………………….. p. 92 Short-term Visiting Scientists …………………………………………………………... p. 99 Long-Term Visiting Scientists …………………………………………………………... p. 117 IRAP Ph. D. Students ……………………………………………………………………. p. 123 IRAP Ph. D. Erasmus Mundus Students………………………………………………. p. 142 Administrative and Secretarial Staff …………………………………………………… p. 156 3 4 ICRANet Faculty Staff Belinski Vladimir ICRANet Bianco Carlo Luciano University of Rome “Sapienza” and ICRANet Einasto Jaan Tartu Observatory, Estonia Novello Mario Cesare Lattes-ICRANet Chair CBPF, Rio de Janeiro, Brasil Rueda Jorge A. University of Rome “Sapienza” and ICRANet Ruffini Remo University of Rome “Sapienza” and ICRANet Vereshchagin Gregory ICRANet Xue She-Sheng ICRANet 5 Adjunct Professors Of The Faculty Aharonian Felix Albert Benjamin Jegischewitsch Markarjan Chair Dublin Institute for Advanced Studies, Dublin, Ireland Max-Planck-Institut für Kernphysis, Heidelberg, Germany Amati Lorenzo Istituto di Astrofisica Spaziale e Fisica Cosmica, Italy Arnett David Subramanyan Chandrasektar- ICRANet Chair University of Arizona, Tucson, USA Chakrabarti Sandip P. Centre for Space Physics, India Chardonnet Pascal Université de la Savoie, France Chechetkin Valeri Mstislav Vsevolodich Keldysh-ICRANet Chair Keldysh institute -

WSOP 2008: Zusammenfassung Der Events #36 Bis #38
WSOP 2008: Zusammenfassung der Events #36 bis #38 Event #36: USD 1.500 No-Limit Hold’em, Tag zwei Beim mittlerweile vierten USD 1.500-No-Limit-Hold’em-Event waren die 187 Spieler für Tag zwei bereits im Geld und diesmal waren auch noch ein paar bekanntere Namen vertreten, wie beispielsweise Team-PokerStars-Pro Luca Pagano, Freddy Deeb, Aaron Kanter, Danny Wong, Isaac Haxton oder Dag Martin Mikkelsen. Ganz nach vorn reichte es für die meisten von ihnen allerdings nicht. Luca Pagano schied auf Platz 149 aus, Mikkelsen wurde 138. (beide kassierten USD 3.340), Freddy Deeb 80. (USD 6.012) und Isaac Haxton erwischte es auf Rang 66 (USD 7.014). Kanter und Wong werden wir dagegen am Final Table wiedersehen. 2005 bekam Aaron Kanter den Spitznamen „The Big Killer“ verpasst. Er spielte damals einen sensationellen Main Event und bugsierte unter anderem Titelverteidiger Greg Raymer sowie Phil Ivey aus dem Turnier. Damals hatte er sich online qualifiziert, belegte schließlich den vierten Platz und kassierte USD 2.000.000 Preisgeld. Zwar spielte er auch danach immer wieder Liveturniere, sein Geld verdient er allerdings weiter beim Onlinepoker. Am Freitag machte er jetzt aber wieder bei der WSOP auf sich aufmerksam und hat den Sprung an den Finaltisch beim USD 1.500 No-Limit Hold’em geschafft. Mit 200.000 in Chips ist er allerdings der Shortstack und hat zudem harte Konkurrenz. Danny Wong aus Los Angeles zum Beispiel, der in seiner noch jungen Karriere schon fast zwei Millionen an Preisgeldern abgeräumt hat. Darunter ein zweiter Platz beim Main Event des Bellagio Cup II im Jahr 2006 für USD 561.115 sowie Siege beim Five Diamond World Poker Classic und bei der Turnierserie Legends of Poker 2007. -

Matt Hawrilenko Siegt Beim World Series of Poker Event #56 – USD 5,000 Six-Handed No Limit Hold’Em
Matt Hawrilenko siegt beim World Series of Poker Event #56 – USD 5,000 Six-handed No Limit Hold’em Matt „Hoss_TBF“ Hawrilenko geht als Nummer 1 bei einem Teilnehmerfeld von insgesamt 928 Spielern hervor. Nach Dutzenden WSOP Cashes und vier Finaltischen hat er nun sein heissersehntes WSOP Gold Bracelet gewonnen und ein sagenhaftes Preisgeld Matt Hawrilenko (Bildquelle: PokerNews.com) von USD 1,003,163. Zweiter wurde Josh Brikis der für seine Platzierung USD 619,609 erhielt. Es wurden im Heads Up Match nur vier Hände gespielt. Die vierte war bereits die Entscheidende. Die Finale Hand: Josh Brikis raiste auf 300,000 vom Small Blind, Matt Hawrilenko reraiste auf 1 Million, Brikis ging all in und Hawrilenko callte. Showdown: Brikis: A [key:card_diamonds] 9 [key:card_diamonds] Hawrilenko: J [key:card_hearts] J [key:card_diamonds] Das Board war 2 [key:card_hearts] 8 [key:card_clubs] 8 [key:card_diamonds] 3 [key:card_spades] 10 [key:card_clubs], dies bedeutete den Sieg für Matt Hawrilenko und als Runner Up ging Josh Brikis hervor. Wie zu erwarten war das Teilnehmerfeld mit Poker Pros dicht bestickt. Darunter sah man unter anderen Shannon Shorr, John Duthie, Juha Helppi, Gavin Griffin, Andy Black, Chris Ferguson, Eli Elezra, Barry Shulman, Matt Graham, Vicky Coren, Marc Naalden, Noah Boeken, Bertrand „ElkY“ Grospellier, Vanessa Rousso, Jennifer Tilly, Scotty Nguyen, Daniel Alaei, Dave Ulliott, Jamie Gold, Tony G, Erik Lindgren, Brandon Cantu, David „Chino“ Rheem, Dario Minieri, Justin Bonomo, Dennis Phillips, Roland de Wolfe, Erich Froehlich, Mike Caro, Marco Traniello, Antonio Esfandiari, Nenad Medic, T.J. Cloutier, Jason Mercier, Gavin Smith, Kirill Gerasimov, Florian Langmann, Ivan Demidov, Allen Cunningham, Daniel Negreanu, Barny Boatman und Isaac Haxton. -

Vous Propose Pour Les Fêtes Une Découverte Originale Des Vins De Bordeaux
PUBLICITE VOUS PROPOSE POUR LES FÊTES UNE DÉCOUVERTE ORIGINALE DES VINS DE BORDEAUX 3 cours du XXX juillet 33 000 Bordeaux [email protected] Tel : 05 56 00 22 85 www.bordeaux.com L’abus d’alcool est dangereux pour la santé. A consommer avec modération Les exclusivités du samedi : une matinée d’initiation à la dégustation des vins de Bordeaux, suivie de trois thématiques au choix L’Oenochef : cours de cuisine avec un atelier accords mets et vins puis un déjeuner De la vigne à la table : repas gourmet dans un restaurant bordelais A partir Les châteaux vous ouvrent leurs portes : repas vigneron suivi d’une visite de la propriété et de 108 € d’une dégustation des vins du château Initiation de 2h Les cours du soir : 4 ateliers de 2h, à raison A partir d’une séance par semaine, de 18h30 à 20h30 ou de 19h à de 190€ tous les derniers samedis du mois 21h, avec au choix : de 15h à 17h La dégustation : un art, une méthode : devenir un dégustateur éclairé 25 € Le Bordeaux, côté pratique : choisir, servir et mettre en scène le vin, de la cuisine à la table Balade oenologique : s’approprier l’histoire du vignoble et toute sa diversité à travers des dégustations comparées Les stages intensifs : en journée, cours sur 2 ou 3 jours consécutifs de 9h30 à 17h, avec au choix La dégustation des Bordeaux, de A à Z : stage technique A partir de 335 € Les secrets des vins de Bordeaux : stage pratique À la rencontre des vins de légende : Les Grands Crus de Bordeaux Renseignements et réservations Maison du Vin, 3 cours du XXX juillet à Bordeaux Tél. -

EUROPEAN POKER TOUR RETURNS to MALTA THIS WEEK Wide Range of New Poker Variants on Offer in Bumper 76-Event Schedule, Multiple Activities Away from the Poker Table
EUROPEAN POKER TOUR RETURNS TO MALTA THIS WEEK Wide Range of New Poker Variants on Offer in Bumper 76-Event Schedule, Multiple Activities Away From The Poker Table ONCHAN, Isle of Man – October 19, 2015 – The European Poker Tour (EPT), an Amaya Inc. (Nasdaq: AYA; TSX: AYA) brand, returns to Malta with a 76-event schedule from October 20-31. The 12-day EPT Malta Poker Festival will once again take place at the Portomaso Casino and partner with the Italian Poker Tour (IPT), which is celebrating its 50th event. The festival, held in conjunction with Pagano Events, begins on October 21 with the €1,100 IPT Main Event, with the EPT €5,300 NL Hold’em Main Event to follow from October 25-31. The EPTLive webcast will broadcast much of the action with Main Event coverage beginning on Day 2 and continuing throughout, including a the cards-up final table. Many poker formats, including 10-Game Mix, HORSE Dealer’s Choice, Quintuple Stud/Draw, Pot Limit Sextuple Omaha and Limit Splitsville Dealer's Choice, are making their EPT debut, having never been played at a PokerStars event before. SPIN & GO LIVE Also making a first appearance at a PokerStars festival is a live version of PokerStars Spin & Go tournaments – hyper-turbo Sit & Go’s that feature a lottery-style prize pool multiplier. Each three- handed super-turbo tournament will feature a €50 buy-in and offer up to 20x the buy-in with a €1,000 top prize. In addition, live Flipout events, popularised on Full Tilt, are also on the schedule. -

Program & Book of Abstracts
PROGRAM & BOOK OF ABSTRACTS published with the contribution of 11th-14th DECEMBER 2019 PROGRAM & BOOK OF ABSTRACTS published with the contribution of 11th-14th DECEMBER, 2019 ORGANIZED BY Prof. Nelson Marmiroli Director CINSA, Consorzio Interuniversitario Nazionale per le Scienze Ambientali Professor Emeritus, University of Parma Prof. Lanfranco Masotti President of Consorzio Italbiotec Prof. Maurizio Filippo Acciarri University of Milano Bicocca © 2019 Nelson Marmiroli, Maurizio Filippo Acciarri, Lanfranco Masotti Published by: Consorzio Interuniversitario Nazionale per le Scienze Ambientali The abstract book is available at www.cinsa.unipr.it (Authors of the single abstracts here published are jointly-responsible for their submitted content) ISBN 978-88-943573-8-7 Institutional P artner With the patronage of Sponsored by Empowering Knowledge Special contribution Preface NANO-DAY IV, December 11-14, 2019 The NANO-DAY conference series was born in Parma (Italy) in 2014 from an idea of Prof. N. Marmiroli and some of his collegues, representing since its biginnig an important meeting point for anybody interested in nanotechnology and nanoscience: academic world, research institutions and industries. Arriving to its fourth edition, the conference was moved to Milano to reach for a vaster international audience. But, the object of the conference remained the same: a platform for young researchers, and for their work. To facilitate the participation, NANO- DAY IV is completely free. NANO-DAY IV is organized jointly by three Institutions: Consorzio Interuniversitario Nazionale per la Scienze Ambientali (CINSA) – Consorzio Italbiotec – University of Milano Bicocca, hosting the event in its premises. The three components of the Organising Committee, Profs Nelson Marmiroli, Lanfranco Masotti and Maurizio Filippo Acciarri, have devised the programme of the conference with the aid of the Steering ans Scientific Committees. -

Official Media Guide
OFFICIAL MEDIA GUIDE 40th ANNUAL WORLD SERIES OF POKER May 26th- July 15, 2009 Rio Hotel, Las Vegas November Nine – November 7-10 www.worldseriesofpoker.com 1 2009 Media Guide Documents: COVER PAGE ................................................................................................................................................................................................ 1 TABLE OF CONTENTS ................................................................................................................................................................................. 2 PR CONTACT SHEET ................................................................................................................................................................................... 3 GENERAL EVENT INFORMATION: FACT SHEET .................................................................................................................................................................................................. 4 SCHEDULE..................................................................................................................................................................................................... 5 SCHEDULE..................................................................................................................................................................................................... 6 SCHEDULE.................................................................................................................................................................................................... -

Pb POKER GENERATION
IRIS FILM e BROS GROUP HOLDING LTD presentano Piero Cardano Andrea Montovoli in POKER GENERATION un film di Fabrizio Crimi & Tiziano Cavaliere diretto da Gianluca Mingotto con Claudio Castrogiovanni Francesca Fioretti Emanuela Rossi Emanuela Postacchini e con Eros Galbiati e la partecipazione straordinaria di Francesco Pannofino e Lina Sastri Distribuzione: Iris Film Durata: 105’ Uscita: Aprile 2012 Ufficio Stampa REGGI&SPIZZICHINO Communication Tel +39 06 97615933 Maya Reggi Raffaella Spizzichino [email protected] www.reggiespizzichino.com Regia Gianluca Mingotto Sceneggiatura Noa Palotto Luciano Federico Marzia De Clercq Tiziano Cavaliere Gianluca Mingotto Fotografia Andrea Rainoldi Musiche Pino Di Pietro Roberto Baeli Montaggio Roberto Baeli Scenografia Fabio Vito Marcello Michelini Gianluca Cisternino Costumi Daniela Antoci Giovanna Armetta Suono Francesco Barletta AntonioD’Andrea Aiuto regia Francesco Aprile Davide Armogida Organizzazione Anna Gandini Pasquale Spadola Simona Visinoni Saverio Nicastro Una Produzione Bros Group Holding LTD Produttore Esecutivo Carlo Di Tullio Prodotto da Fabrizio Crimi Distribuito da Iris Film Ufficio Stampa Iris REGGI&SPIZZICHINO Communication CAST TECNICO Durata 105' 2 CAST ARTISTICO Filo Piero Cardano Tony Andrea Montovoli Anna Francesca Fioretti Rosario Francesco Pannofino Lucia Lina Sastri Brigitte Emanuela Rossi Joyce Claudio Castrogiovanni Sandro Eros Galbiati Samantha Emanuela Postacchini GIOCATORI PROFESSIONISTI POKER Patrik Antonious Fabrizio Baldassari Luca Pagano Filippo Candio Maurizio Agrello Dario Minieri Salvatore Bonavena Mustapha Kanit Marco Bognanni Daniele Amatruda 3 SINOSSI In una famiglia povera residente in un paesino siciliano, vivono due fratelli, l'uno l'opposto dell'altro. Il più grande, Tony (Andrea Montovoli), è un fanatico dei film sulla mala americana e sogna di diventare un giocatore di poker professionista, l'altro, Filo (Piero Cardano), è un genio introverso e scontroso, la sua sindrome semi-autistica lo porta ad analizzare l'ambiente che lo circonda in modo ossessivo e meccanico. -

Leo Wolpert Gewinnt Event #29 Der 2009 World Series of Poker
Leo Wolpert gewinnt Event #29 der 2009 World Series Of Poker Von Lilly Wolf 256 Spieler gingen an den Start von Event #29, dem USD 10,000 World Championship Heads Up No Limit Hold’em Turnier der 2009 WSOP. Darunter Chris Ferguson, Greg Raymer, Barry Greenstein, Jason Mercier, Tom Dwan, Sami „LarsLuzak“ Kelopuro, JC Tran, Leo Wolpert Peter Eastgate, Dario Minieri, Evelyn Ng, Erick Lindgren, Phil Hellmuth, Michael Mizrachi, Benny Spindler, Johnny Chan, John Duthie, Michael Pesek, Johannes Steindl und Vanessa Rousso. Den Sieg holte sich Leo Wolpert, der sich ein Preisgeld in Höhe von USD 639,331 und sein erstes goldenes WSOP Bracelet sicherte. In der finalen Hand limpte Leo Wolpert und John Duthie checkte, Am Flop kam 10 [key:card_spades] 3 [key:card_spades] 5 [key:card_clubs] und Duthie checkte. Wolpert setzte 120,000 und Duthie annoncierte sofort „All-Iin.“ Wolpert callte. Duthie: 10 [key:card_diamonds] 2 [key:card_hearts] Wolpert: 3 [key:card_hearts] 5 [key:card_hearts] Turn und River brachten mit J [key:card_hearts] und Q [key:card_hearts] den zweiten Platz und ein Preisgeld in Höhe von USD 386,636, für den EPT Gründer John Duthie. Das Ergebnis: 1. USD 625,682 Leo Wolpert 2. USD 386,636 John Duthie 3. USD 214,289 Jamin Stokes 4. USD 214,289 Nathan Doudney 5. USD 92,580 Johnny Chan 6. USD 92,580 Dustin Woolf 7. USD 92,580 Steve O’Dwyer 8. USD 92,580 Bryan Pellegrino 9. USD 38,424 Roberto Romanello 10. USD 38,424 Clavet Mathieu Der deutsche Spieler Benny Spindler spielte am ersten Tag gegen Phil Hellmuth. -
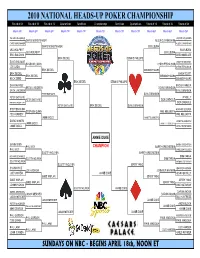
2010 Nhupc Brackets
2010 NATIONAL HEADS-UP POKER CHAMPIONSHIP Round of 64 Round of 32 Round of 16 Quarterfinals Semifinals Championship Semifinals Quarterfinals Round of 16 Round of 32 Round of 64 March 5th March 6th March 6th March 7th March 7th March 7th March 7th March 7th March 6th March 6th March 5th PATRIK ANTONIUS JESPER HOUGAARD CHRIS MONEYMAKER ALLEN CUNNINGHAM CHRIS MONEYMAKER ALLEN CUNNINGHAM CHRIS MONEYMAKER ELI ELEZRA LEO WOLPERT ELI ELEZRA LEO WOLPERT ELI ELEZRA ERIC BALDWIN GREG MUELLER ERIK SEIDEL DENNIS PHILLIPS DAVID WILLIAMS ANNETTE DWORSKI DAVID WILLIAMS CHRIS FERGUSON JOE CADA CHRIS FERGUSON ERIK SEIDEL DENNIS PHILLIPS ERIK SEIDEL KARA SCOTT ERIK SEIDEL DENNIS PHILLIPS HUCK SEED DENNIS PHILLIPS ERIK SEIDEL DENNIS PHILLIPS DAN RAMIREZ BROCK PARKER ERICK LINDGREN DOYLE BRUNSON ERICK LINDGREN DOYLE BRUNSON PETER EASTGATE DOYLE BRUNSON PETER EASTGATE JP KELLY PETER EASTGATE DON CHEADLE BERTRAND GROSPELLIER DON CHEADLE PETER EASTGATE ERIK SEIDEL DOYLE BRUNSON STEPHEN QUINN HOWARD LEDERER STEPHEN QUINN PHIL HELLMUTH TED FORREST PHIL HELLMUTH JAMIE GOLD ANNETTE OBRESTAD DARIO MINIERI ANNETTE OBRESTAD JAMIE GOLD ANNETTE OBRESTAD JAMIE GOLD OREL HERSHISER ANNIE DUKE GAVIN SMITH BARRY GREENSTEIN PHIL IVEY CHAMPION BARRY GREENSTEIN PHIL IVEY VANESSA ROUSSO SCOTTY NGUYEN BARRY GREENSTEIN RICHARD EDWARDS SAM FARHA SCOTTY NGUYEN SAM FARHA SCOTTY NGUYEN ANTONIO ESFANDIARI SCOTTY NGUYEN JERRY YANG SHAWN RICE JENNIFER HARMAN JOE HACHEM JENNIFER HARMAN JOE HACHEM ANNIE DUKE JENNIFER TILLY GABE KAPLAN JERRY YANG GABE KAPLAN JERRY YANG GABE KAPLAN JERRY YANG JOHNNY CHAN MIKE MATUSOW SCOTTY NGUYEN ANNIE DUKE DANIEL NEGREANU DARVIN MOON JASON MERCIER DARVIN MOON JASON MERCIER BILL HUNTRESS JASON MERCIER ANNIE DUKE PIETER de KORVER ANDY BLOCH PIETER de KORVER ANNIE DUKE MIKE SEXTON ANNIE DUKE JASON MERCIER ANNIE DUKE PHIL GORDON ANDREW WILSON PHIL GORDON PAUL WASICKA TOM DWAN PAUL WASICKA PHIL LAAK PAUL WASICKA PHIL LAAK GUS HANSEN PHIL LAAK GUS HANSEN JOHN JUANDA GREG RAYMER SUNDAYS ON NBC - BEGINS APRIL 18th, NOON ET. -
Montepremi Milionario Al Casinò Di Sanremo Per La Finale Del Pokerstar.It
1 Montepremi milionario al Casinò di Sanremo per la finale del Pokerstar.it di Laura Bissolotti – 05 Aprile 2008 – 17:23 Al Casinò di Sanremo l'americano Jason Mercier vince il premio finale di 869 mila euro del Pokestars European Poker Tour, sbaragliando la concorrenza di più di 700 giocatori, tra i quali 222 italiani, provenienti da tutto il mondo che dal 1 fino al 5 aprile si sono sfidati per conquistare un posto in prima fila intorno all'ambitissimo cash table quasi milionario. I magnifici 8 aspiranti campioni che si sono contesi fino all'ultima chip il sostanzioso payout – in assoluto il quarto più alto di tutto il PokerStars EPT – sono stati: gli italiani Dario Minieri (23 anni) e Gregory Genovese (37 anni), Jason Mercier (USA, 21 anni), Antony Lellouche (Francia, 28), Eric Koskas (Francia, 35 anni), William Thorson (Svezia, 25 anni), Dag Palovic (Slovacchia, 33) e Marcus Bower (USA, 24). Ad "accontentarsi" del secondo e terzo premio, rispettivamente di505 mila euro e 287.600,00 euro, sono stati Antony Lellouche e il romano Dario Minieri, mentre a dividersi quello che restava dei 3,5 milioni di euro di montepremi sono stati i primi 72 classificati – tra cui 18 italiani – con premi via via inferiori fino all'ultimo che torna a casa con 5.750 euro. I primi due italiani della lunga classifica sono Dario Minieri del Team PokerStars e Gregory Genovese, entrambi di Roma e tifosi romanisti. Dario è uno dei giocatori più conosciuti e Riviera24 - 1 / 2 - 02.10.2021 2 seguiti del mondo del poker sin da quando aveva poco più di 16 anni e in 2 anni ha accumulato circa 300 mila dollari di premi per tornei vinti in tutto il mondo.