DOCSLIB.ORG

Model Development and Evaluation in Northeast China

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Model Development and Evaluation in Northeast China PUBLICATIONS Journal of Advances in Modeling Earth Systems RESEARCH ARTICLE Modeling irrigation-based climate change adaptation in 10.1002/2014MS000402 agriculture: Model development and evaluation in Northeast Key Points: China This study developed a coupled crop production and river circulation Masashi Okada1, Toshichika Iizumi1, Gen Sakurai1, Naota Hanasaki2, Toru Sakai1, Katsuo Okamoto1, model and Masayuki Yokozawa3 The model can accurately capture the major features of hydrology and 1National Institute for Agro-Environmental Sciences, Tsukuba, Japan, 2National Institute for Environmental Studies, crop yield 3 The model is useful in assessing Tsukuba, Japan, Graduate School of Engineering, Shizuoka University, Hamamatsu, Japan climate change adaptation based on irrigation Abstract Replacing a rainfed cropping system with an irrigated one is widely assumed to be an effective Supporting Information: measure for climate change adaptation. However, many agricultural impact studies have not necessarily Supporting Information S1 accounted for the space-time variations in the water availability under changing climate and land use. Figure S1 Moreover, many hydrologic and agricultural assessments of climate change impacts are not fully integrated. Figure S2 Figure S3 To overcome this shortcoming, a tool that can simultaneously simulate the dynamic interactions between crop production and water resources in a watershed is essential. Here we propose the regional production Correspondence to: and circulation coupled model (CROVER) by embedding the PRYSBI-2 (Process-based Regional Yield Simula- M. Yokozawa, tor with Bayesian Inference version 2) large-area crop model into the global water resources model (called [email protected] H08), and apply this model to the Songhua River watershed in Northeast China. The evaluation reveals that the model’s performance in capturing the major characteristics of historical change in surface soil moisture, Citation: river discharge, actual crop evapotranspiration, and soybean yield relative to the reference data during the Okada, M., T. Iizumi, G. Sakurai, N. Hanasaki, T. Sakai, K. Okamoto, and interval 1979–2010 is satisfactory accurate. The simulation experiments using the model demonstrated that M. Yokozawa (2015), Modeling subregional irrigation management, such as designating the area to which irrigation is primarily applied, irrigation-based climate change has measurable influences on the regional crop production in a drought year. This finding suggests that adaptation in agriculture: Model development and evaluation in reassessing climate change risk in agriculture using this type of modeling is crucial not to overestimate Northeast China, J. Adv. Model. Earth potential of irrigation-based adaptation. Syst., 7, 1409–1424, doi:10.1002/ 2014MS000402. Received 6 NOV 2014 Accepted 28 AUG 2015 1. Introduction Accepted article online 1 SEP 2015 Published online 24 SEP 2015 Many studies have widely deemed that replacing a rainfed cropping system with an irrigated one can be an effective measure for climate change adaptation [Porter et al., 2014; Challinor et al., 2014]. This is true as long as this replacement does not lead to unsustainable water extraction and/or as long as there is still suffi- cient irrigation water available [Elliott et al., 2014]. However, many agricultural impact assessments have used time-constant future irrigation scenarios derived from statistical data or other independent studies (some exceptional integrated studies are seen in Deryng et al. [2011], Biemans et al. [2013], and Kummu et al. [2014]). General hydrologic models or land-surface models have been used to assess the hydrologic impacts due to climate change [Doll€ and Schmied, 2012; Hagemann et al., 2013; Hanasaki et al., 2013]. These hydro- logic models have been intensively tested for their ability in capturing the major components of terrestrial water cycling, including river discharge, actual evapotranspiration, and soil moisture [Alcamo et al., 2003; Hanasaki et al., 2008; Biemans et al., 2009], but have not necessarily been evaluated for their ability in simu- lating crop growth and yield (a few exceptions are seen in Bondeau et al. [2007] and Biemans et al. [2013]). VC 2015. The Authors. Although a recent study combines the outputs of the hydrologic models and crop models to evaluate the This is an open access article under the potential impacts of water availability on future crop productivity [Elliott et al., 2014], the hydrologic models terms of the Creative Commons and crop models are separately simulated and thus still has not yet fully integrated. These facts necessitate Attribution-NonCommercial-NoDerivs License, which permits use and an improved assessment of potential crop production under changing climate, varying water availability, distribution in any medium, provided and expanding irrigated cropland areas, using a tool that can simultaneously simulate the dynamic interac- the original work is properly cited, the tions between crop production and water resources (e.g., river water) in a watershed. use is non-commercial and no modifications or adaptations are China is the leading crop-producing country worldwide and accounted for 20% of global cereal production made. in 2011 [Food and Agriculture Organization of the United Nations, 2014]. The Northeast China Plain is a major OKADA ET AL. MODELING IRRIGATION-BASED ADAPTATION 1409 Journal of Advances in Modeling Earth Systems 10.1002/2014MS000402 crop-producing region and important for maintaining China’s food balance. However, the recent warming and drying trends in Northeast China are evident [Tao et al., 2003; Piao et al., 2010; Yu et al., 2014]. These changes in climate have likely led to an increase in the extent of drought-damage cropland area and a decrease in the area suitable for cultivation of some crops, such as spring wheat [Jiao et al., 2007, 2008]. A decreasing trend in water resources, including the river discharge of the Songhua and Liao Rivers, which are major river channels in this region, has accompanied these changes, increasing concerns about food supply in the coming decades [Piao et al., 2010]. Hence, it is valuable to revisit the following questions that are posed in a series of previous studies [Jimenez Cisneros et al., 2014; Porter et al., 2014], using North- east China as the example: Is the available water resources sufficient for crop production under changing climate and expanding irrigated area? Given the pressure to maintain the increasing food demand in China, how much can subregional irrigation management increase the total crop production in a given watershed? To address these issues, this study (1) developed the regional production and circulation coupled model (CROVER) that can simultaneously simulate crop growth and yield, river discharge and their dynamic inter- actions by embedding the PRYSBI-2 large-area crop model [Sakurai et al., 2014] into the H08 global water resources model [Hanasaki et al., 2008]; (2) applied this coupled model to the Songhua River watershed in Northeast China and evaluated the model’s performance by comparing the historical model simulation, including soybean yield, river discharge, surface soil moisture, actual crop evapotranspiration, with the ref- erence data; (3) performed simulation experiments using the coupled model to quantify the possible influ- ence of subregional irrigation management in a drought year on regional crop production. 2. Study Area Our study area includes the Northeast China Plain, the main portion of which is located in the cool- temperate and partially semiarid zones and is surrounded by three mountain ranges: the Daxing’anling, Xiaoxing’anling, and Chanbai Mountains (Figure 1a). The main watersheds consist of the Songhua and Liao Rivers. The Songhua River flows across the Northeast China Plain from west to east after its tribu- taries join at its upper stream (Figure 1b). The riverhead of the tributary flowing from the north side (called the Nen River) is located in the Daxing’anling and Xiaoxing’anling Mountains, whereas that of the tributary flowing from the south side (called the Second Songhua River) is located in the Chanbai Mountains. The areal extent of the Songhua River watershed reaches 545,000 km2 (supporting informa- tion Figure S1a), and the total river length is 1927 km. The river flow is mainly sourced from precipita- tion in summer (which accounts for 60–80% of the annual runoff [Asian Development Bank, 2005]) and snowmelt from March to May. The mean quantity of water resources in the Songhua River watershed and its surrounding small watersheds in 2002–2011 is approximately 130 3 109 m3 [Ministry of Water Resources of the People’s Republic of China (MWR), 2015]. Twenty-four percent of the water resources (31 3 109 m3) are consumed by agriculture [MWR, 2015]. Two reservoirs with the storage capacity of >109 m3, the Baishan and Fengman reservoirs, are located in the upper stream of the watershed (Fig- ure 1b). The Northeast China Plain is the largest crop-producing region in China. Among other crops, soybean pro- duced in this region accounted for approximately 40% of the national production in 2011 [National Bureau of Statistics of China (NBSC), 2014]. Therefore, soybean was selected for this study. Soybean is mainly culti- vated in the northern part of the watershed (Figure 1a). The Liao River and its watershed were thus excluded from the analysis. 3. Data and Model 3.1. General Description of the CROVER Model As schematically
Load more

Recommended publications
  • The Human Threat to River Ecosystems at the Watershed Scale: an Ecological Security Assessment of the Songhua River Basin, Northeast China
    water Article The Human Threat to River Ecosystems at the Watershed Scale: An Ecological Security Assessment of the Songhua River Basin, Northeast China Yuan Shen 1,2, Huiming Cao 1, Mingfang Tang 1 and Hongbing Deng 1,* 1 State Key Laboratory of Urban and Regional Ecology, Research Center for Eco-Environmental Sciences, Chinese Academy of Sciences, Beijing 100085, China; [email protected] (Y.S.); [email protected] (H.C.); [email protected] (M.T.) 2 University of Chinese Academy of Sciences, Beijing 100049, China * Correspondence: [email protected]; Tel.: +86-10-6284-9112 Academic Editor: Sharon B. Megdal Received: 6 December 2016; Accepted: 13 March 2017; Published: 16 March 2017 Abstract: Human disturbances impact river basins by reducing the quality of, and services provided by, aquatic ecosystems. Conducting quantitative assessments of ecological security at the watershed scale is important for enhancing the water quality of river basins and promoting environmental management. In this study, China’s Songhua River Basin was divided into 204 assessment units by combining watershed and administrative boundaries. Ten human threat factors were identified based on their significant influence on the river ecosystem. A modified ecological threat index was used to synthetically evaluate the ecological security, where frequency was weighted by flow length from the grids to the main rivers, while severity was weighted by the potential hazard of the factors on variables of river ecosystem integrity. The results showed that individual factors related to urbanization, agricultural development and facility construction presented different spatial distribution characteristics. At the center of the plain area, the provincial capital cities posed the highest level of threat, as did the municipal districts of prefecture-level cities.
    [Show full text]
  • Surface Modelling of Human Population Distribution in China
    Ecological Modelling 181 (2005) 461–478 Surface modelling of human population distribution in China Tian Xiang Yuea,∗, Ying An Wanga, Ji Yuan Liua, Shu Peng Chena, Dong Sheng Qiua, Xiang Zheng Denga, Ming Liang Liua, Yong Zhong Tiana, Bian Ping Sub a Institute of Geographical Sciences and Natural Resources Research, Chinese Academy of Sciences, 917 Building, Datun, Anwai, Beijing 100101, China b College of Science, Xi’an University of Architecture and Technology, Xi’an 710055, China Received 24 March 2003; received in revised form 23 April 2004; accepted 4 June 2004 Abstract On the basis of introducing major data layers corresponding to net primary productivity (NPP), elevation, city distribution and transport infrastructure distribution of China, surface modelling of population distribution (SMPD) is conducted by means of grid generation method. A search radius of 200 km is defined in the process of generating each grid cell. SMPD not only pays attention to the situation of relative elements at the site of generating grid cell itself but also calculates contributions of other grid cells by searching the surrounding environment of the generating grid cell. Human population distribution trend since 1930 in China is analysed. The results show that human population distribution in China has a slanting trend from the eastern region to the western and middle regions of China during the period from 1930 to 2000. Two scenarios in 2015 are developed under two kinds of assumptions. Both scenarios show that the trends of population floating from the western and middle regions to the eastern region of China are very outstanding with urbanization and transport development.
    [Show full text]
  • Detection of Sensitive Soil Properties Related to Non-Point Phosphorus
    Ecological Indicators 60 (2016) 483–494 Contents lists available at ScienceDirect Ecological Indicators j ournal homepage: www.elsevier.com/locate/ecolind Detection of sensitive soil properties related to non-point phosphorus pollution by integrated models of SEDD and PLOAD a,b,∗ c a a,d Chen Lin , Zhipeng Wu , Ronghua Ma , Zhihu Su a Key Laboratory of Watershed Geographic Sciences, Institute of Geography and Limnology, Chinese Academy of Sciences, Nanjing 210008, China b State Key Laboratory of Soil and Sustainable Agriculture, Institute of Soil Science, Chinese Academy of Sciences, Nanjing 210008, China c School of Geographic and Oceanographic Sciences, Nanjing University, Nanjing 210046, China d College of Geography and Environmental Sciences, Zhejiang Normal University, Jinhua, Zhejiang Province 321004, China a r a t i c l e i n f o b s t r a c t Article history: Effectively identifying soil properties in relation to non-point source (NPS) phosphorus pollution is impor- Received 2 March 2015 tant for NPS pollution management. Previous studies have focused on particulate P loads in relation to Received in revised form 7 July 2015 agricultural non-point source pollution. In areas undergoing rapid urbanization, dissolved P loads may be Accepted 26 July 2015 important with respect to conditions of surface infiltration and rainfall runoff. The present study devel- oped an integrated model for the analysis of both dissolved P and particulate P loads, applied to the Keywords: 2 Meiliang Bay watershed, Taihu Lake, China. The results showed that NPS P loads up to 15 kg/km were Non-point source pollution 2 present, with particulate P loads up to 13 kg/km .
    [Show full text]
  • Water Pollution and Health Impact in China: a Mini Review Wen-Qing Lu*, Shao-Hua Xie, Wen-Shan Zhou, Shao-Hui Zhang, Ai-Lin Liu
    Open Environmental Sciences, 2008, 2, 1-5 1 Open Access Water Pollution and Health Impact in China: A Mini Review Wen-Qing Lu*, Shao-Hua Xie, Wen-Shan Zhou, Shao-Hui Zhang, Ai-Lin Liu Department of Occupational and Environmental Health, MOE Key Lab of Environment and Health, School of Public Health, Tongji Medical College, Huazhong University of Science and Technology, Wuhan, Hubei, China Abstract: For the last 20-odd years in China, an economic boom has resulted in severe environmental pollution; water pollution, particularly, is of great concern. It has been reported that pollution in China’s overall surface water is rated me- dium. The water quality of groundwater, lakes and reservoirs has deteriorated. Consequently, such a general distribution of water pollution has posed a grave threat to public health in China. The health impact of water pollution has been docu- mented in the last several decades; these documents are reviewed in this paper on several outstanding aspects, including chronic mercurialism, arsenism, cancers related to microcystins, health problems caused by organic pollutants and water pollution accidents as well. Indubitably, water pollution and its health impact remain enormous challenges in China. Keywords: Water pollution, health impact, public health. In the last 20-odd years, there has been a boom in eco- induced water shortage have been the two biggest factors nomic development in China. However, a side effect that has restricting sustainable development in China. resulted in is the increased severity of environmental pollu- Water Pollution tion. Water pollution, especially, poses a grave threat to pub- lic health. The security of drinking water is not satisfactory.
    [Show full text]
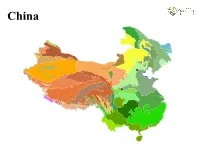
  • R Graphics Output
    China China LEGEND Previously sampled Malaise trap site Ecoregion Alashan Plateau semi−desert North Tibetan Plateau−Kunlun Mountains alpine desert Altai alpine meadow and tundra Northeast China Plain deciduous forests Altai montane forest and forest steppe Northeast Himalayan subalpine conifer forests Altai steppe and semi−desert Northern Indochina subtropical forests Amur meadow steppe Northern Triangle subtropical forests Bohai Sea saline meadow Northwestern Himalayan alpine shrub and meadows Central China Loess Plateau mixed forests Nujiang Langcang Gorge alpine conifer and mixed forests Central Tibetan Plateau alpine steppe Ordos Plateau steppe Changbai Mountains mixed forests Pamir alpine desert and tundra Changjiang Plain evergreen forests Qaidam Basin semi−desert Da Hinggan−Dzhagdy Mountains conifer forests Qilian Mountains conifer forests Daba Mountains evergreen forests Qilian Mountains subalpine meadows Daurian forest steppe Qin Ling Mountains deciduous forests East Siberian taiga Qionglai−Minshan conifer forests Eastern Gobi desert steppe Rock and Ice Eastern Himalayan alpine shrub and meadows Sichuan Basin evergreen broadleaf forests Eastern Himalayan broadleaf forests South China−Vietnam subtropical evergreen forests Eastern Himalayan subalpine conifer forests Southeast Tibet shrublands and meadows Emin Valley steppe Southern Annamites montane rain forests Guizhou Plateau broadleaf and mixed forests Suiphun−Khanka meadows and forest meadows Hainan Island monsoon rain forests Taklimakan desert Helanshan montane conifer forests
    [Show full text]
  • The World Bank
    Uocument of The World Bank FOR OFFICIAL USE ONLY Public Disclosure Authorized Report No. 11040-A STAFF APPRAISAL REPORT Public Disclosure Authorized CHINA CHANGCCUNWATER SUPPLY AND ENVIRONMENTALPROJECT DECEMBER30, 1992 Public Disclosure Authorized MITCOFICHE COPY heport No.:11040-CHA Type: (OAR) Titie: CHANGCHUN WATER SUIPPLY AND) ENV Autthor: PIETVELD, C Ext.:82924 Room:F8059 Dept.:ASTIN Environment, %uman Resources and Urban Development Operations Division Country Department II Public Disclosure Authorized East Asia and Pacific Regional Office This docunent hs a resMtded distibuto and may be uad by ripiens only in the perfonmnce of their offid dutie Its contens may not otheise be dbcosed without Word Bank autoization. CURRENCY EQUIVALENTS (As of June 1992) CurrencyName = Renminbi(RMB) Currency Unit = Yuan (Y) $1.00 =Y 5.48 Y 1.00 = $0.18 WEIGHTS AND MEASURES 1 millimeter(mm) = 0.0939 Inches (in) 1 meter (m) = 3.2808 feet (ft) I squaremeter (m: 2) = 10.7639square feet (ft) I cubicmeter (ml) = 35.3 cubicfeet 1 hectare(ha) = 10,000square meters 1 kilometer(Iam) = 0.62 miles(mi) 1 squarekilometer (1an) = 0.3861square mile (mtn) ACRONYNS AND ABBREVIATIONS CIDA CanadianInternational Development Agency CMC ChinaNational Machinery Import and ExportCorporation CSC ChangchunSewerage Company CWSC ChangchunWater Supply Company CWRC CbangchunWater Resources Company EPB EnvironmentalProtecion Buream HLLG High-LevelLeadership Group lcd Litersper capitaper day MOC Ministryof Construction MOWC Ministryof WaterConservancy NEPA NationalEnviromnental Protection
    [Show full text]
  • Harbin Information Pack Harbin, Also Known As the 'Paris of the East'
    Harbin Information Pack Harbin, also known as the ‘Paris of the East’. Content Page About Harbin- History Local amenities and facilities – Health, leisure and shopping. Expat – What it is and groups. Climate and lifestyle. Cost of living. Local attractions. Tourist attractions- Harbin and other cities Public transport. About Harbin Harbin is the capital of Heilongjiang Province and located in the northeast of the northeast China Plain. Harbin is famous as a historical and cultural city and renowned for its snow and ice culture. Harbin is also well known for its large number of European-style buildings. Harbin is also known as the ice city. Through the winter Harbin displays thousands of ice sculptures and has hundreds of ice-related activities. Harbin’s History Harbin’s history isn’t as long as some cities. The city is around 110 years old and has become the biggest city in the north-eastern section of China with currently over 10 million people. Harbin was originally a fishing village until the Russians started to build a railroad into the area in1897. Local amenities and facilities Harbin has many shops and leisure facilities available. There are many different places to go shopping but the most famous shopping streets are: Zhongyang Dajie (Central street)- Full of new shopping malls such as Euro Plaza, Parksons, and Lane Crawford that carry international brands and are expensive. There are Nike stores, KFC and interesting Russian thrift stores. The streets are lined with beer gardens during the summer as Harbin is the 3rd biggest city for beer consumption. Guogeli Dajie- The area around here is dotted with Russian buildings and large shopping complexes.
    [Show full text]
  • Coal, Water, and Grasslands in the Three Norths
    Coal, Water, and Grasslands in the Three Norths August 2019 The Deutsche Gesellschaft für Internationale Zusammenarbeit (GIZ) GmbH a non-profit, federally owned enterprise, implementing international cooperation projects and measures in the field of sustainable development on behalf of the German Government, as well as other national and international clients. The German Energy Transition Expertise for China Project, which is funded and commissioned by the German Federal Ministry for Economic Affairs and Energy (BMWi), supports the sustainable development of the Chinese energy sector by transferring knowledge and experiences of German energy transition (Energiewende) experts to its partner organisation in China: the China National Renewable Energy Centre (CNREC), a Chinese think tank for advising the National Energy Administration (NEA) on renewable energy policies and the general process of energy transition. CNREC is a part of Energy Research Institute (ERI) of National Development and Reform Commission (NDRC). Contact: Anders Hove Deutsche Gesellschaft für Internationale Zusammenarbeit (GIZ) GmbH China Tayuan Diplomatic Office Building 1-15-1 No. 14, Liangmahe Nanlu, Chaoyang District Beijing 100600 PRC [email protected] www.giz.de/china Table of Contents Executive summary 1 1. The Three Norths region features high water-stress, high coal use, and abundant grasslands 3 1.1 The Three Norths is China’s main base for coal production, coal power and coal chemicals 3 1.2 The Three Norths faces high water stress 6 1.3 Water consumption of the coal industry and irrigation of grassland relatively low 7 1.4 Grassland area and productivity showed several trends during 1980-2015 9 2.
    [Show full text]
  • Monitoring Population Evolution in China Using Time-Series DMSP/OLS Nightlight Imagery
    remote sensing Article Monitoring Population Evolution in China Using Time-Series DMSP/OLS Nightlight Imagery Sisi Yu 1,2, Zengxiang Zhang 1 and Fang Liu 1,* 1 Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China; [email protected] (S.Y.); [email protected] (Z.Z.) 2 University of Chinese Academy of Sciences, Beijing 100049, China * Correspondence: [email protected]; Tel.: +86-10-6488-9205; Fax: +86-10-6488-9203 Received: 16 November 2017; Accepted: 26 January 2018; Published: 28 January 2018 Abstract: Accurate and detailed monitoring of population distribution and evolution is of great significance in formulating a population planning strategy in China. The Defense Meteorological Satellite Program’s Operational Linescan System (DMSP/OLS) nighttime lights time-series (NLT) image products offer a good opportunity for detecting the population distribution owing to its high correlation to human activities. However, their detection capability is greatly limited owing to a lack of in-flight calibration. At present, the synergistic use of systematically-corrected NLT products and population spatialization is rarely applied. This work proposed a methodology to improve the application precision and versatility of NLT products, explored a feasible approach to quantitatively spatialize the population to grid units of 1 km × 1 km, and revealed the spatio-temporal characteristics of population distribution from 2000 to 2010. Results indicated that, (1) after inter-calibration, geometric, incompatibility and discontinuity corrections, and adjustment based on vegetation information, the incompatibility and discontinuity of NTL products were successfully solved. Accordingly, detailed actual residential areas and luminance differences between the urban core and the peripheral regions could be obtained.
    [Show full text]
  • Quantifying Contributions of Climate Change and Local Human Activities to Runoff Decline in the Second Songhua River Basin
    water Article Quantifying Contributions of Climate Change and Local Human Activities to Runoff Decline in the Second Songhua River Basin Bao Shanshan 1 , Yang Wei 1, Wang Xiaojun 2,3 and Li Hongyan 1,* 1 Key Laboratory of Groundwater Resources and Environment, Jilin Provincial Key Laboratory of Water Resources and Environment, Jilin University, Changchun 130021, China; [email protected] (B.S.); [email protected] (Y.W.) 2 State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, China; [email protected] 3 Research Center for Climate Change, Ministry of Water Resources, Nanjing 210029, China * Correspondence: [email protected]; Tel.: +86-137-5625-7761 Received: 29 July 2020; Accepted: 15 September 2020; Published: 23 September 2020 Abstract: In the past several decades, climate change and human activities have influenced hydrological processes, and potentially caused more frequent and extensive flood and drought risks. Therefore, identification and quantification of the driving factors of runoff variation have become a hot research area. This paper used the trend analysis method to show that runoff had a significant downward trend during the past 60 years in the Second Songhua River Basin (SSRB) of Northeast China. The upper, middle, and lower streams of five hydrological stations were selected to analyze the breakpoint of the annual runoff in the past 60 years, and the breakpoints were used to divide the entire study period into two sub-periods (1956–1974 and 1975–2015). Using the water–energy coupling balance method based on Choudhury–Yang equation, the climatic and catchment landscape elasticity coefficient of the annual runoff change was estimated, and attribution analysis of the runoff change was carried out for the Fengman Reservoir and Fuyu stations in SSRB.
    [Show full text]
  • Cropland Heterogeneity Changes on the Northeast China Plain in the Last Three Decades (1980S–2010S)
    Cropland heterogeneity changes on the Northeast China Plain in the last three decades (1980s–2010s) Xiaoxuan Liu1,2, Le Yu1,2,3, Qinghan Dong4, Dailiang Peng5, Wenbin Wu6, Qiangyi Yu6, Yuqi Cheng1,2, Yidi Xu1,2, Xiaomeng Huang1,2, Zheng Zhou1, Dong Wang1,7, Lei Fang8 and Peng Gong1,2 1 Department of Earth System Science, Ministry of Education Key Laboratory for Earth System Modeling, Tsinghua University, Beijing, China 2 Joint Center for Global Change Studies, Beijing, China 3 Ministry of Education Ecological Field Station for East Asian Migratory Birds, Beijing, China 4 Department of Remote Sensing Boeretang 200, Flemish Institute of Technology (VITO), Mol, Belgium 5 Institute of Remote Sensing and Digital Earth,Chinese Academy of Sciences, Key Laboratory of Digital Earth Science, Beijing, China 6 Ministry of Agriculture and Rural Affairs/Institute of Agricultural Resources and Regional Planning, Chinese Academy of Agricultural Sciences, Key Laboratory of Agricultural Remote Sensing (AGRIRS), Beijing, China 7 National Supercomputing Center in Wuxi, Wuxi, China 8 Chinese Academy Sciences, CAS Key Laboratory of Forest Ecology and Management, Institute of Applied Ecology, Shenyang, China ABSTRACT The Northeast China Plain is one of the major grain-producing areas of China because of its fertile black soil and large fields adapted for agricultural machinery. It has experienced some land-use changes, such as urbanization, deforestation, and wetland reclamation in recent decades. A comprehensive understanding of these changes in terms of the total cropping land and its heterogeneity during this period is important for policymakers. In this study, we used a series of cropland products at the 30- m resolution for the period 1980–2015.
    [Show full text]
  • Research Article Thyroid-Disrupting Activities of Groundwater from A
    Hindawi Journal of Chemistry Volume 2020, Article ID 2437082, 9 pages https://doi.org/10.1155/2020/2437082 Research Article Thyroid-Disrupting Activities of Groundwater from a Riverbank Filtration System in Wuchang City, China: Seasonal Distribution and Human Health Risk Assessment Dongdong Kong,1 Hedan Liu,1 Yun Liu,2 Yafei Wang,1 and Jian Li 1 1Engineering Research Center of Groundwater Pollution Control and Remediation, Ministry of Education, College of Water Sciences, Beijing Normal University, Beijing 100875, China 2South China Institute of Environmental Science, MEE, No. 7 West Street, Yuancun, Guangzhou 510655, China Correspondence should be addressed to Jian Li; [email protected] Received 25 July 2019; Accepted 11 December 2019; Published 7 January 2020 Guest Editor: Lisa Yu Copyright © 2020 Dongdong Kong et al. )is is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. )e recombinant thyroid hormone receptor (TR) gene yeast assay was used to evaluate thyroid disruption caused by groundwater from the riverbank filtration (RBF) system in Wuchang City, China. To investigate seasonal fluctuations, groundwater was collected during three seasons. Although no TR agonistic activity was found, many water samples exhibited TR antagonistic activity. )e bioassay-derived amiodarone hydrochloride (AH) equivalents ranged from 2.99 to 274.40 μg/L. Water samples collected from the riverbank filtration system during the dry season had higher TR antagonistic activity. All samples presented adverse 3,3′,5-triiodo-L-thyronine (T3) equivalent levels, ranging from − 2.00 to − 2.12 μg/kg.
    [Show full text]