Pg-Qp – 29 *Pgqp29*
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
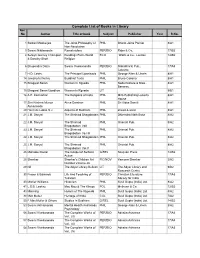
Complete List of Books in Library Acc No Author Title of Book Subject Publisher Year R.No
Complete List of Books in Library Acc No Author Title of book Subject Publisher Year R.No. 1 Satkari Mookerjee The Jaina Philosophy of PHIL Bharat Jaina Parisat 8/A1 Non-Absolutism 3 Swami Nikilananda Ramakrishna PER/BIO Rider & Co. 17/B2 4 Selwyn Gurney Champion Readings From World ECO `Watts & Co., London 14/B2 & Dorothy Short Religion 6 Bhupendra Datta Swami Vivekananda PER/BIO Nababharat Pub., 17/A3 Calcutta 7 H.D. Lewis The Principal Upanisads PHIL George Allen & Unwin 8/A1 14 Jawaherlal Nehru Buddhist Texts PHIL Bruno Cassirer 8/A1 15 Bhagwat Saran Women In Rgveda PHIL Nada Kishore & Bros., 8/A1 Benares. 15 Bhagwat Saran Upadhya Women in Rgveda LIT 9/B1 16 A.P. Karmarkar The Religions of India PHIL Mira Publishing Lonavla 8/A1 House 17 Shri Krishna Menon Atma-Darshan PHIL Sri Vidya Samiti 8/A1 Atmananda 20 Henri de Lubac S.J. Aspects of Budhism PHIL sheed & ward 8/A1 21 J.M. Sanyal The Shrimad Bhagabatam PHIL Dhirendra Nath Bose 8/A2 22 J.M. Sanyal The Shrimad PHIL Oriental Pub. 8/A2 Bhagabatam VolI 23 J.M. Sanyal The Shrimad PHIL Oriental Pub. 8/A2 Bhagabatam Vo.l III 24 J.M. Sanyal The Shrimad Bhagabatam PHIL Oriental Pub. 8/A2 25 J.M. Sanyal The Shrimad PHIL Oriental Pub. 8/A2 Bhagabatam Vol.V 26 Mahadev Desai The Gospel of Selfless G/REL Navijvan Press 14/B2 Action 28 Shankar Shankar's Children Art FIC/NOV Yamuna Shankar 2/A2 Number Volume 28 29 Nil The Adyar Library Bulletin LIT The Adyar Library and 9/B2 Research Centre 30 Fraser & Edwards Life And Teaching of PER/BIO Christian Literature 17/A3 Tukaram Society for India 40 Monier Williams Hinduism PHIL Susil Gupta (India) Ltd. -

Faculty Profile
FACULTY PROFILE * NAME . : DR. PARASHURAM. G. MALAGE MA. Ph.D. SLET. B.Ed. Dip.in Ambedkar studies * DESIGNATION : ASSISTANT PROFESSOR * ADDRESS : H.O.D. of HINDI and ASSISTANT PROFESSOR BESANT WOMEN'S COLLEGE, KODIALBAIL MANGALORE -575003 * CELL.NO : 8277156735 / 9008371806 * EMAIL : [email protected] * EDUCATIONAL QULIFICATION : DEGREE INSTITUTION YEAR UG - BA KarnatakaUniversityDharawad 1998 PG - MA ” 2000 Ph.D ” 2006 SLET Govt.of Karnataka 2000 B.Ed Karnataka University Darawad 2009 * CAREER PROFILE : * Presently working with Department of Hindi, Besant Women's College, and Mangalore. * TEACHING EXPERIENCE : 15 Year's. 12 YEAR'S in UG colleges. 04 YEAR'S in PG (Karnataka university Dharawad and kuvempu university Shivamogga ). * SUBJECT TAUGHT : HINDI * MEMBER OF BORDS : 1.Member of the Board of Examination in MA (Hindi – PG) during 2016 . 2. Member of Advisory Committee, PG Dept.of Hindi Mangalore University. * PUBLICATION PROFILE : Under Publication 1) Study material for MA (Final year) and BA (final year. Opt.Hindi) (DDE - Kuvempu Univ ersity Shankarghatta - Shivamogga). 2) Study material for MA (final year ) - (Karnataka State Open University - Mysor ). 3) Study material for MA ( First year ) (DDE- Mangaluru University, Mangaluru ) *Research Paper : Research paper published in book - Bharatiy bhashaon mein Ramnath(Kannada bhasha) ISBN no -978-93-5229-053-6 , Title -"Ramkath par adharit 'shudra tapasvi' Kavya natak. * AREA OF INTEREST : Hindi Literature and Linguistic. * ACADEMIC ACHIEVEMENT : 1. Participated in National Seminar, Jointly organize by Bharathiy Hindi Prishad, Allahabad and Dept. of Hindi K U Dharawad. 2. Participated in Two days National Seminar Organized by Dakshin Bharath Hindi Prachar Sabha Madras,Dharawad Branch. 3. Participated and Presented the Paper entitle " Mahadevi Varma ke kavya me Vedhana bhav" in One day National Seminar on Literature of Mahadevi varma, organized by Dept. -

4Th Mahadevi Verma Memorial Lecture Series
SECTION I ON MAHADEVI VERMA MAHADEVI VERMA ON EDUCATION SHANKAR SHARAN1 Today's graduate has to think ... those who have all the worldly facilities want our life values. Why should those who already have such values consider themselves poor? (Mahadevi Verma) Mahadevi believed that a person is always a student in the realm of thought and of feelings. If not, then somewhere he must have closed the door of his heart and mind. She was renowned as a poetess, but in fact, she devoted a lot of time during her life to education and teaching. She had established the Prayag Mahila Vidyapeeth, which she served for as long as she could. Few people know that her devotion to education was a conscious choice as she believed that educational institutions built the nation and some of her great contemporaries have noted that. Sachchidanand Vatsyayan 'Agyeya' drew attention to the fact that according to Mahadevi, her poetry was the reflection of her moments of leisure and 'she would devote the rest of her life to the field of education, where it was required.'2 There are many definitions of 'Vidya' (knowledge/ education) in Indian literature. What Mahadevi liked the most was 'Sa Vidya Ya Vimuktye' – which means 'education is that which liberates'. She noted that in the past, Indian scholars had a very special regard for education and that is why it was always kept under state control. 1. Dr Shankar Sharan is a Lecturer in the Department of Educational Research and Policy Perspective at NCERT, New Delhi. 2. Agyeya, "Adhunik Kavi: Mahadevi Varma" in Trishanku (Surya Prakashan Mandir; 1973), p. -

Of Contemporary India
OF CONTEMPORARY INDIA Catalogue Of The Papers of Prabhakar Machwe Plot # 2, Rajiv Gandhi Education City, P.O. Rai, Sonepat – 131029, Haryana (India) Dr. Prabhakar Machwe (1917-1991) Prolific writer, linguist and an authority on Indian literature, Dr. Prabhakar Machwe was born on 26 December 1917 at Gwalior, Madhya Pradesh, India. He graduated from Vikram University, Ujjain and obtained Masters in Philosophy, 1937, and English Literature, 1945, Agra University; Sahitya Ratna and Ph.D, Agra University, 1957. Dr. Machwe started his career as a lecturer in Madhav College, Ujjain, 1938-48. He worked as Literary Producer, All India Radio, Nagpur, Allahabad and New Delhi, 1948-54. He was closely associated with Sahitya Akademi from its inception in 1954 and served as Assistant Secretary, 1954-70, and Secretary, 1970-75. Dr. Machwe was Visiting Professor in Indian Studies Departments at the University of Wisconsin and the University of California on a Fulbright and Rockefeller grant (1959-1961); and later Officer on Special Duty (Language) in Union Public Service Commission, 1964-66. After retiring from Sahitya Akademi in 1975, Dr. Machwe was a visiting fellow at the Institute of Advanced Studies, Simla, 1976-77, and Director of Bharatiya Bhasha Parishad, Calcutta, 1979-85. He spent the last years of his life in Indore as Chief Editor of a Hindi daily, Choutha Sansar, 1988-91. Dr. Prabhakar Machwe travelled widely for lecture tours to Germany, Russia, Sri Lanka, Mauritius, Japan and Thailand. He organised national and international seminars on the occasion of the birth centenaries of Mahatma Gandhi, Rabindranath Tagore, and Sri Aurobindo between 1961 and 1972. -

Following Are Some of the Books by Indian Authors Book Name Author
Following are some of the books by Indian Authors Book Name Author A bend in the river V.S. Naipal A brush with life Satish Gujral A House of Mr. Biswar V.S. Naipal A Million Mutinies Now V.S. Naipal A Passage to England Nirad C.Chodhury A Prisoner’s Scrapbook L.K. Advani A River Sutra Gita Mehra A sense of time H.S.Vatsyayan A strange and subline address Amit Chaudhary A suitable boy Vikram Seth A village by the sea Anita Desai A voice for freedom Nayantara Sehgal Aansoo Suryakant Tripathi Nirala Afternoon Raag Amit Chaudhari Ageless Body, Timeless Mind Deepak Chopra Agni Veena Kazi Nazrul Islam Ain-i-Akbari Abul Fazal Amar Kosh Amar Singh An autobiography Jawaharlal Nehru An Equal Music Vikram Seth An Idealist View of life Dr. S. Radhakrishan Amrit Aur Vish Amrit Lal Nagar Anamika Suryakant Tripathi Nirala Anandmath Bankim Chandra Chatterjee Areas of Darkness V.S. Naipal Arthashastra Lautilya Ashtadhyayi Panini Autobiography of an Unknown India Nirad C. Choudhury Bandicoot Run Manohar Malgonkar Beginning of the Beginning Bhagwan Shri Rajneesh Between the Lines Kuldip Nayyar Beyond Modernisation, Beyond Self Sisirkumar Ghose Bhagvad Gita Ved Vyas Bharat Bharati Maithilisharan Gupt Bharat Durdasha Bhartendu Harischandra Border and Boundaries: women in India’s Ritu Menon & Kamla Bhasin Partition Bharat Bharati Maithili Saran Gupt Breaking the Silence Anees Jung Bride and the Sahib and the other stories Khushwant Singh Broken Wings Sarojini Naidu Bubble, The Mulk Raj Anand Buddha Charitam Ashwaghosh By God’s Decree Kapil Dev Chandalika Rabindra Nath Tagore Chandrakanta Santati Devkinandan Khatri Chemmen: Thakazhi Sivasankara Pillai Chitra Rabindranath Tagore Chitralekha Bhagwati Charan Verma Chitrangada Rabindra Nath Tagore Circle of Reason Amitav Ghosh Clear Light of Day Anita Desai Confessions of a Lower Mulk Raj Anand Confrontation with Pakistan B. -

Language and Literature
1 Indian Languages and Literature Introduction Thousands of years ago, the people of the Harappan civilisation knew how to write. Unfortunately, their script has not yet been deciphered. Despite this setback, it is safe to state that the literary traditions of India go back to over 3,000 years ago. India is a huge land with a continuous history spanning several millennia. There is a staggering degree of variety and diversity in the languages and dialects spoken by Indians. This diversity is a result of the influx of languages and ideas from all over the continent, mostly through migration from Central, Eastern and Western Asia. There are differences and variations in the languages and dialects as a result of several factors – ethnicity, history, geography and others. There is a broad social integration among all the speakers of a certain language. In the beginning languages and dialects developed in the different regions of the country in relative isolation. In India, languages are often a mark of identity of a person and define regional boundaries. Cultural mixing among various races and communities led to the mixing of languages and dialects to a great extent, although they still maintain regional identity. In free India, the broad geographical distribution pattern of major language groups was used as one of the decisive factors for the formation of states. This gave a new political meaning to the geographical pattern of the linguistic distribution in the country. According to the 1961 census figures, the most comprehensive data on languages collected in India, there were 187 languages spoken by different sections of our society. -

TIWARI-DISSERTATION-2014.Pdf
Copyright by Bhavya Tiwari 2014 The Dissertation Committee for Bhavya Tiwari Certifies that this is the approved version of the following dissertation: Beyond English: Translating Modernism in the Global South Committee: Elizabeth Richmond-Garza, Supervisor David Damrosch Martha Ann Selby Cesar Salgado Hannah Wojciehowski Beyond English: Translating Modernism in the Global South by Bhavya Tiwari, M.A. Dissertation Presented to the Faculty of the Graduate School of The University of Texas at Austin in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy The University of Texas at Austin December 2014 Dedication ~ For my mother ~ Acknowledgements Nothing is ever accomplished alone. This project would not have been possible without the organic support of my committee. I am specifically thankful to my supervisor, Elizabeth Richmond-Garza, for giving me the freedom to explore ideas at my own pace, and for reminding me to pause when my thoughts would become restless. A pause is as important as movement in the journey of a thought. I am thankful to Martha Ann Selby for suggesting me to subhead sections in the dissertation. What a world of difference subheadings make! I am grateful for all the conversations I had with Cesar Salgado in our classes on Transcolonial Joyce, Literary Theory, and beyond. I am also very thankful to Michael Johnson and Hannah Chapelle Wojciehowski for patiently listening to me in Boston and Austin over luncheons and dinners respectively. I am forever indebted to David Damrosch for continuing to read all my drafts since February 2007. I am very glad that our paths crossed in Kali’s Kolkata. -

List of Registered Candidates 2021-22
THE HERITAGE SCHOOL D2, Vasant Kunj, New Delhi-110070 Pre-School Admission :Session 2021-22 List of Registered Candidates with Score Registration Number Name Father Name Mother Name Total Score THSV21REG12 SUVAM GARG TEJESH GARG MANU DOGRA 40 THSV21REG13 AADIT DOGRA RAJAT DOGRA PRIYANKA DOGRA 50 THSV21REG14 SPARSH BHARDWAJ ANKIT BHARDWAJ POORNIMA SINGH 50 THSV21REG15 ZORAWAR SINGH AHUJA MANDEEP SINGH AHUJA PANSY KAUR 20 THSV21REG16 WARIS SINGH AHUJA MANDEEP SINGH AHUJA PANSY KAUR 20 THSV21REG17 AVYAAN MALIK GANDHARV MALIK SHIKHA MALIK 50 THSV21REG18 PRANIT LATH MUKUL LATH MANSI LATH 20 THSV21REG19 ZAVIAN KRISHAN SINGH NAKUL KRISHAN SINGH AVANI SINGH 50 THSV21REG20 OMAV GUPTA JATIN GUPTA AKRITI GUPTA 20 THSV21REG21 ADVITH YADAV ATUL YADAV AISHWARYARANI HEGDE 80 THSV21REG22 NITARA TRIPATHI NITISH TRIPATHI JHILMIL TRIPATHI 30 THSV21REG23 CAHIRA SINGH NARULA SUDEEP SINGH NARULA KAVERI SUDEEP NARULA 70 THSV21REG24 PRIYANSH PRATAP VIJAY PRATAP MONICA VERMA 40 THSV21REG25 SAMAKSH KALRA SAMEER KALRA IBHA KALRA 50 THSV21REG26 NATHANIEL WINNIE THOMAS WINNIE THOMAS SOUMYA WINNIE THOMAS 40 THSV21REG27 ADVAY GAUR VINEET GAUR SHAIFALI SHARMA 50 THSV21REG28 AADVAN PRASAD AKHLESH PRASAD NEHA KUMARI SHAW 40 THSV21REG29 KIARA GAUTAM ABHAY GAUTAM RIDHI GAUTAM 20 THSV21REG30 VIRAANSH SOOD VIKRANT SOOD RUPALI MALIK 50 THSV21REG31 DIVRAJ SINGH JOLLY AMANBIR SINGH JOLLY AMRITA KAUR 20 THSV21REG32 REYAN JHA ANJANI KUMAR ROUSHAN BABITA JHA 50 THSV21REG33 REUBEN SINGH GURPREET SINGH HAOBAM LINTHOINGAMBI CHANU 40 THSV21REG35 REYANSH MOHAN SHAH SAMEER SHAH SABITA -
![Amrita Pritam[1919-2005 ] Amrita Pritam](https://docslib.b-cdn.net/cover/4945/amrita-pritam-1919-2005-amrita-pritam-914945.webp)
Amrita Pritam[1919-2005 ] Amrita Pritam
Amrita Pritam Born in Pakistan (Gujranwala) in 1919. Death in India in 2005. Quote on feminism: “There are many stories which are not on paper. They’re written in the bodies and minds of women”. Amrita Pritam Amrita Pritam[1919-2005 ] Amrita Pritam She received the Padma Shri and Padma Vibhushana in 1969 and Sahitya Akademi comradeship in 2004. She got D.Litt. honorory degrees from many universities. She becomes a member of Rajya Sabha in 1986-92. In 2007, 'Amrita recited by Gulzar' was released by Gulzar. Amrita Pritam as a Novelist • Amrita Pritam was the first prominent Panjabi woman novelist. • Her work; 'Lok Peeth' (People's • She wrote novels and essays. Anguish) frankly criticises the battle She was famous for her short and torn economy after the Bengal stories, autobiographies and famine of 1943. poems. • After independence in 1947, Amrita migrated to Delhi. She has been • She wrote the poem on the writing over the partition. division of Punjab. ► As a famous and notable writer, her ► Her novel 'Pinjar' (The stories turned into Skeleton) 1970, is an award films. winning Hindi movie by Chandra Prakash Dwivedi. ► Her novel Pinjar (The Skeleton, 1970) is ► This film was full of filmed. humanism. ► The film presents the picture of the suffering of both communities of India and Pakistan. Amrita and Partition of India ◼ Amrita shows human psychology of the religious fantasy. She gave the word of women's painful condition during that time. She becomes a voice of all feminizes. She disapproves the religious fantasy people through her own series of literature. -

States of Affect: Trauma in Partition/Post-Partition South Asia
STATES OF AFFECT: TRAUMA IN PARTITION/POST-PARTITION SOUTH ASIA By Rituparna Mitra A DISSERTATION Submitted to Michigan State University in partial fulfillment of the requirements for the degree of English – Doctor of Philosophy 2015 ABSTRACT STATES OF AFFECT: TRAUMA IN PARTITION/POST-PARTITION SOUTH ASIA By Rituparna Mitra The Partition of the Indian subcontinent – into India and Pakistan in 1947 – was one of the crucial moments marking the break between the colonial and postcolonial era. My project is invested in exploring the Partition not merely in terms of the events of August 1947, but as an ongoing process that continues to splinter political, cultural, emotional and sexual life-worlds in South Asia. My dissertation seeks to map analytical pathways to locate the Partition and the attendant formations of minoritization and sectarian violence as continuing, unfolding processes that constitute postcolonial nation-building. It examines the far-reaching presence of these formations in current configurations of politics, culture and subjectivity by mobilizing the interdisciplinary scope of affect-mediated Trauma and Memory Studies and Postcolonial Studies, in conjunction with literary analysis. My project draws on a wide range of cultural artifacts such as poetry, cantillatory performance, mourning rituals, testimonials, archaeological ruins, short stories and novels to develop a heuristic and affective re-organization of post-Partition South Asia. It seeks to illuminate through frameworks of memory, melancholia, trauma, affect and postcoloniality how the ongoing effects of the past shape the present, which in turn, offers us ways to reimagine the future. This dissertation reaches out to recent work developing a vernacular framework to analyze violence, trauma and loss in South Asia. -

Amrita Pritam: the Revenue Stamp and Harivanshraibachchan: in the Afternoon of Time • Chapter III
Chapter Three Amrita Pritam: The Revenue Stamp and HarivanshRaiBachchan: In the Afternoon of Time • Chapter III (i) AmritaPritam '.The Revenue Stamp (ii) Hariwansh Rai Bachchan: In the Afternoon of Time The present chapter discusses those two writers who have made a mark in the Hterature of their regional languages, and consequently in India and abroad. Amrita Pritam is the first woman writer in the Punjabi literature emerged as a revolutionary poet and novelist who illuminated the predicament of women caused by shackles of traditions and patriarchy. Harvansh Rai Bachchan is the important name in the movement of 'Nayi Kavita'. He created a new wave of poetry among the admirers by his book Madhushala. With the publication of this book, he became one of the most admired poets in Hindi literary world. Amrita Pritam was a prolific writer and a versatile genius. She published more than 100 books of poetry, fiction, biographies, essays, translations of foreign writers' works, such as Bulgarian poets Iran Vazovand Haristobotev, a Hungarian poet Attila Josef etc., as well as a collection of Punjabi folk songs and autobiographies. Apart from The Revenue Stamp, she wrote one more autobiography Aksharon Ke Sayen (Shadows of Words) published in 1999.She was a rebel who lived her life in her own way with utmost intensity. This intensity, this passion is the soul of her writing. Before we plunge into a detailed discussion of her autobiography vis-a-vis her writings, it is useful to understand how she grew as an individual, what forces shaped her character and her mind, which people she learned from and grew as a writer. -

Assistant Port Conservator Department.Pmd
Assistant Port Conservator (Department of Port)/ Female Matron (Technical Education Department) 1. Vegetarian is related to meat as..... is related to liquor. (a) Drunkard (b) Patient (c) Teetotaler (d) Sportsman 2. A person who sacrifices his life for a cause is called a .... (a) Victim (b) Martyr (c) Terrorist (d) Revolutionary 3. A person who is facing trail before a criminal court is called .... (a) A culprit (b) An accomplice (c) An accused (d) A prisoner 4. Find the odd one out: (a) Dignity (b) Wisdom (c) Intelligence (d) Honesty 5. Which of the following words cannot be formed from the letters used in the word EXAMINATION ? (a) MAINTAIN (b) MAXIMUM (c) NOMINATION (d) TAXATION 6. In a certain code language “lim suk ta” means ‘boys are clever’, “din lim pu” means “girls are tall” and “pu ne ta” means “boys and girls”. Which word in that language means “and” ? (a) lim (b) din (c) ta (d) ne 7. Which of the following series obeys the rule, “Number of letters skipped in between adjacent letter is two”? (a) MPSVY (b) EHKMP (c) DGJLO (d) XVRQOP 8. Which of the following series starts with a vowel and then has consonants appearing alternately with vowels? (a) Emulsion (b) Iteration (c) Alemot (d) Violence 9. Coconut : Shell : : Letter : ...............? (a) Envelope (b) Mail (c) Stamp (d) Letterbox 10. If a “rectangle” is called a “circle”; a “circle” is called a “point”; a “point” is called a “triangle”; a “triangle” is called a “square”; then, a “wheel” is to be called (a) Rectangle (b) Circle (c) Point (d) Triangle 11.