DOCSLIB.ORG

A. Earth Geometry and Geodesy ADVANCED DIGITAL EARTH

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A. Earth Geometry and Geodesy ADVANCED DIGITAL EARTH ADVANCED DIGITAL EARTH A. Earth Geometry and Geodesy Outline • Representaon of Earth (Latude and Longitude) • Determining Latude • Time Zones and the Longitude Problem • Maps • Map Projec)ons • Coordinate Systems • Map Scale • Georeferencing • Earth Shape: Sphere and Ellipsoid, Datum and Geoid Representa?ons of Earth What if you wanted to travel from San Diego to London, England? What path would you take? Which direc)on yields the shortest distance? The shortest distance between any two points is a straight line. But how do you draw a straight line on a globe? For that maer, how can you navigate upon a sphere, at all? Certainly, traveling to London, England is not as simple as saying, “Take a right turn at the Atlan)c Ocean.” The way that we have overcome this apparent problem is with the geographic grid. The geographic grid divides the world into both northern/ southern components (la-tude) and eastern/western components (longitude). The range of latude is from 0° (the Equator) to 90° North and South Latude. The range of longitude is from 0° (the Prime Meridian) to 180° (the Internaonal Date Line). Lines of latude are known as parallels. Lines of longitude are known as meridians. Every place on Earth has a geographic grid coordinate. For example, San Diego, California is located at 32° North Latude, 117° West Longitude. Diagram of Latude 90 degrees North Lat. = North Pole 90 degrees 0 degrees Lat. = Equator 45 degrees 45th Parallel 45 degrees South Latude North Pole 180°Longitude = Internaonal Date Line 90° West Longitude 180° 90° 90° East Longitude 0° Longitude = Prime Meridian View from above the North Pole (NP) 180 Long 135 West Long 135 East Long Diagram of Longitude 90 West Long NP 90 East Long 45 West Long 45 East Long 0 Long Please click on the following link to watch a video lecture that describes and explains Latude and Longitude: hNps://www.youtube.com/watch?v=9vfQM_M1Pec Determining Latude The use of the North Celes)al Pole star for navigaon purposes has been used for thousands of years. In par)cular, the posi)on of the North Star (Polaris) will tell you your latude (whereas a good clock will help you to determine your longitude). Finding Polaris Little Dipper Big Dipper Time Zones There are 24 )me zones in the world; each )me zone is separated by 15° (the world turns 360° per 24 hours = 15° rotaon per hour) (see Figure 3 on next slide). If you are west of the Prime Meridian (west of 0° Longitude), you are behind GMT (Greenwich Mean Time). If you travel east of the Prime Meridian, you are ahead GMT (remember, the Sun rises in the east and sets in the west due to Earth’s easterly – or, counterclockwise -- rotaon). In the example below, the )me for the person at the Prime Meridian is solar noon. For the person standing in the east, the )me is aernoon (no)ce the Sun is in the western, seng sky). For the person standing in the west, the )me is before noon (no)ce the Sun is in the eastern, rising sky). Direc)on of Sun (rises in the east and sets in the west) West Prime Meridian East If you cross the IDL (Internaonal Date Line = 180°) from the Western Hemisphere into the Eastern Hemisphere, you lose a day (set your calendar ahead a day). If you cross the IDL from the Eastern Hemisphere into the Western Hemisphere, you gain a day (set your calendar back a day). Figure 3 World Poli)cal Time Zones (adopted from Encarta Encyclopedia, 2000) -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10 +11 +12 As you can see from the above )me zone map, the 15° rule is not always followed! Why not? Please click on the following link to watch a video lecture that describes and explains Time Zones: hNps://www.youtube.com/watch?v=OXuc84bP90k Early Voyage Problem: Longitude! How do you find East/West? Key = Time Just as you use longitudinal distance to calculate )me, you can also use )me difference to calculate your longitude! The relaonship between )me and longitude (1 hour = 15°) is the key. If you know the difference in )me between two places, and you know the longitude of one place, you can calculate the longitude of the other. For example, imagine you are a sailor and you need to know where you are (you don’t have a GPS unit!). You find your latude by no)cing the posi)on of the North Star above your horizon. To determine longitude, however, you must use a clock. Assume you leave San Diego. You set your clock to San Diego )me and set sail. Eventually, you want to determine your locaon. On your boat, you no)ce when the shadow is shortest on the mast (the Sun is at its highest point in the sky). It is solar noon. You check your clock. It reads 8 am. If it is noon for you and 8 am in San Diego, you are ahead of San Diego )me (you are east of San Diego) by 4 hours. 4 x 15 = 60°. Therefore, you are located 60° east of San Diego, which means you are at 120° - 60° = 60° West Longitude: In the Early days of sea voyages, determining longitude was a difficult task. Why? How do you read a pendulum clock at sea! A contest was created by England with the following results. We can thank John Harrison for our wristwatch. Chronometer #1: Finished in 1735 AD Chronometer #4: Finished in 1760 AD Please click on the following link to watch a video lecture that describes and explains The Longitude Problem: hNps://www.youtube.com/watch?v=s4hsI3Cz2tg Maps The map is the primary tool of the geographer….It can * fit in a pocket * give locaon * provide area data * be themac (such as weather maps, veg maps, soil maps…) Mapping: Projecons and Coordinates • There are many reasons for wan)ng to project the Earth’s surface onto a flat plane, rather than deal with the curved surface. – The paper used to output GIS maps is flat. – Flat maps are scanned and digi)zed to create GIS databases. – The Earth has to be projected to see all of it at once. – It’s much easier to measure distance on a plane. Projecons (cont.) • A transformaon of the spherical or ellipsoidal earth onto a flat map is called a map projec)on. • The map projec)on can be onto a flat surface or a surface that can be made flat by cung, such as a cylinder or a cone. • If the globe, aer scaling, cuts the surface, the projec)on is called secant. Lines where the cuts take place or where the surface touches the globe have no projec)on distor)on. From: hNp://naonalatlas.gov/ar)cles/mapping/a_projec)ons.html Projecons (cont.) • Projec)ons can be based on axes parallel to the earth's rotaon axis (equatorial), at 90 degrees to it (transverse), or at any other angle (oblique). • A projec)on that preserves the shape of features across the map is called conformal. • A projec)on that preserves the area of a feature across the map is called equal area or equivalent. • No flat map can be both equivalent and conformal. Most fall between the two as compromises. • To compare or edge-match maps in a GIS, both maps MUST be in the same projec)on. Distorons • Any projec)on must distort the Earth in some way • Two types of projec)ons are important in GIS – Conformal property: Shapes of small features are preserved: anywhere on the projec)on the distor)on is the same in all direcons. – Equal area property: Shapes are distorted, but features have the correct area. – Both types of projec)ons will generally distort distances. Map Projec?ons Flaen half of a rubber ball? No. Instead, features are projected onto one of three “developable” surfaces. Planar: a map projec)on Cylindrical: a map projec)on where the Conic: a map projec)on where the earth’s surface is resul)ng from the earth’s surface is projected onto a tangent projected onto a tangent or secant cone, which is conceptual projec)on of the or secant cylinder, which is then cut then cut from apex to base and laid flat earth onto a tangent or lengthwise and laid flat secant plane hNp://www.naonalatlas.gov/ar)cles/mapping/a_projec)ons.html#two 21" Conformal Projecon •! Cylindrical projecon •! Parallels and meridians at right angles. •! Angles and shapes of small objects preserved (at every point, east–west scale same as north–south scale). •! The size/shape/area of large Example: Mercator projec?on (1569) objects distorted. used for nau)cal purposes (constant •! Seldom used for world maps. courses are straight lines). 22" Equivalent Projec?on •! Conic projecon •! Preserves accurate area. •! Scale and shape are not preserved. Example: Albers Equal Area standard projec)on for US Geological Survey, US Census Bureau 23" Compromise Projecons •! Neither equivalent nor conformal. •! Meridians curve gently, avoiding extremes. •! Doesn’t preserve proper)es, but looks right. Example: Robinson projec?on (1961) • Good compromise projecon for ! viewing enre world. • Used by Rand McNally and the Naonal ! Geographic Society. 24" Cylindrical Projecons •! Conceptualized as the result of wrapping a cylinder of paper around the Earth. •! The Mercator projec)on is the best- known cylindrical projec)on. –! The cylinder is wrapped around the Equator. –! The projec)on is conformal. •! At any point scale is the same in both direc)ons.
Load more

Recommended publications
  • TYPHOONS and DEPRESSIONS OVER the FAR EAST Morning Observation, Sep Teinber 6, from Rasa Jima Island by BERNARDF
    SEPTEMBER1940 MONTHLY WEATHER REVIEW 257 days west of the 180th meridian. In American coastal appear to be independent of the typhoon of August 28- waters fog was noted on 10 days each off Washington and September 5, are the following: The S. S. Steel Exporter California; on 4 days off Oregon; and on 3 days off Lower reported 0700 G. C. T. September 6, from latitude 20'18' California. N., longitude 129'30'E.) a pressure of 744.8 mm. (993.0 nib.) with west-northwest winds of force 9. Also, the TYPHOONS AND DEPRESSIONS OVER THE FAR EAST morning observation, Sep teinber 6, from Rasa Jima Island By BERNARDF. DOUCETTE, J. (one of the Nansei Island group) was 747.8 mm. (997.0 5. mb.) for pressure and east-northeast, force 4, for winds. [Weather Bureau, Manila, P. I.] Typhoon, September 11-19) 1940.-A depression, moving Typhoon, August %!-September 6,1940.-A low-pressure westerly, passed about 200 miles south of Guam and area far to the southeast of Guam moved west-northwest, quickly inclined to the north, intensifying to typhoon rapidly developing to typhoon intensity as it proceeded. strength, September 11 to 13. It was stationary, Sep- When the center reached the regions about 250 miles tember 13 and 14, about 150 miles west-northwest of west of Guam, the direction changed to the northwest, Guam, and then began a northwesterly and northerly and the storm continued along this course until it reached course to the ocean regions about 300 miles west of the the latitude of southern Formosa.
    [Show full text]
  • AIM: Latitude and Longitude
    AIM: Latitude and Longitude Latitude lines run east/west but they measure north or south of the equator (0°) splitting the earth into the Northern Hemisphere and Southern Hemisphere. Latitude North Pole 90 80 Lines of 70 60 latitude are 50 numbered 40 30 from 0° at 20 Lines of [ 10 the equator latitude are 10 to 90° N.L. 20 numbered 30 at the North from 0° at 40 Pole. 50 the equator ] 60 to 90° S.L. 70 80 at the 90 South Pole. South Pole Latitude The North Pole is at 90° N 40° N is the 40° The equator is at 0° line of latitude north of the latitude. It is neither equator. north nor south. It is at the center 40° S is the 40° between line of latitude north and The South Pole is at 90° S south of the south. equator. Longitude Lines of longitude begin at the Prime Meridian. 60° W is the 60° E is the 60° line of 60° line of longitude west longitude of the Prime east of the W E Prime Meridian. Meridian. The Prime Meridian is located at 0°. It is neither east or west 180° N Longitude West Longitude West East Longitude North Pole W E PRIME MERIDIAN S Lines of longitude are numbered east from the Prime Meridian to the 180° line and west from the Prime Meridian to the 180° line. Prime Meridian The Prime Meridian (0°) and the 180° line split the earth into the Western Hemisphere and Eastern Hemisphere. Prime Meridian Western Eastern Hemisphere Hemisphere Places located east of the Prime Meridian have an east longitude (E) address.
    [Show full text]
  • The Longitude of the Mediterranean Throughout History: Facts, Myths and Surprises Luis Robles Macías
    The longitude of the Mediterranean throughout history: facts, myths and surprises Luis Robles Macías To cite this version: Luis Robles Macías. The longitude of the Mediterranean throughout history: facts, myths and sur- prises. E-Perimetron, National Centre for Maps and Cartographic Heritage, 2014, 9 (1), pp.1-29. hal-01528114 HAL Id: hal-01528114 https://hal.archives-ouvertes.fr/hal-01528114 Submitted on 27 May 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. e-Perimetron, Vol. 9, No. 1, 2014 [1-29] www.e-perimetron.org | ISSN 1790-3769 Luis A. Robles Macías* The longitude of the Mediterranean throughout history: facts, myths and surprises Keywords: History of longitude; cartographic errors; comparative studies of maps; tables of geographical coordinates; old maps of the Mediterranean Summary: Our survey of pre-1750 cartographic works reveals a rich and complex evolution of the longitude of the Mediterranean (LongMed). While confirming several previously docu- mented trends − e.g. the adoption of erroneous Ptolemaic longitudes by 15th and 16th-century European cartographers, or the striking accuracy of Arabic-language tables of coordinates−, we have observed accurate LongMed values largely unnoticed by historians in 16th-century maps and noted that widely diverging LongMed values coexisted up to 1750, sometimes even within the works of one same author.
    [Show full text]
  • Prime Meridian ×
    This website would like to remind you: Your browser (Apple Safari 4) is out of date. Update your browser for more × security, comfort and the best experience on this site. Encyclopedic Entry prime meridian For the complete encyclopedic entry with media resources, visit: http://education.nationalgeographic.com/encyclopedia/prime-meridian/ The prime meridian is the line of 0 longitude, the starting point for measuring distance both east and west around the Earth. The prime meridian is arbitrary, meaning it could be chosen to be anywhere. Any line of longitude (a meridian) can serve as the 0 longitude line. However, there is an international agreement that the meridian that runs through Greenwich, England, is considered the official prime meridian. Governments did not always agree that the Greenwich meridian was the prime meridian, making navigation over long distances very difficult. Different countries published maps and charts with longitude based on the meridian passing through their capital city. France would publish maps with 0 longitude running through Paris. Cartographers in China would publish maps with 0 longitude running through Beijing. Even different parts of the same country published materials based on local meridians. Finally, at an international convention called by U.S. President Chester Arthur in 1884, representatives from 25 countries agreed to pick a single, standard meridian. They chose the meridian passing through the Royal Observatory in Greenwich, England. The Greenwich Meridian became the international standard for the prime meridian. UTC The prime meridian also sets Coordinated Universal Time (UTC). UTC never changes for daylight savings or anything else. Just as the prime meridian is the standard for longitude, UTC is the standard for time.
    [Show full text]
  • Spherical Coordinate Systems
    Spherical Coordinate Systems Exploring Space Through Math Pre-Calculus let's examine the Earth in 3-dimensional space. The Earth is a large spherical object. In order to find a location on the surface, The Global Pos~ioning System grid is used. The Earth is conventionally broken up into 4 parts called hemispheres. The North and South hemispheres are separated by the equator. The East and West hemispheres are separated by the Prime Meridian. The Geographic Coordinate System grid utilizes a series of horizontal and vertical lines. The horizontal lines are called latitude lines. The equator is the center line of latitude. Each line is measured in degrees to the North or South of the equator. Since there are 360 degrees in a circle, each hemisphere is 180 degrees. The vertical lines are called longitude lines. The Prime Meridian is the center line of longitude. Each hemisphere either East or West from the center line is 180 degrees. These lines form a grid or mapping system for the surface of the Earth, This is how latitude and longitude lines are represented on a flat map called a Mercator Projection. Lat~ude , l ong~ude , and elevalion allows us to uniquely identify a location on Earth but, how do we identify the pos~ion of another point or object above Earth's surface relative to that I? NASA uses a spherical Coordinate system called the Topodetic coordinate system. Consider the position of the space shuttle . The first variable used for position is called the azimuth. Azimuth is the horizontal angle Az of the location on the Earth, measured clockwise from a - line pointing due north.
    [Show full text]
  • THE EARTH. MERIDIANS and PARALLELS 2=Meridian (Geography)
    THE EARTH. MERIDIANS AND PARALLELS 1=Circle of latitude 2=Meridian (geography) A circle of latitude , on the Earth , is an imaginary east -west circle connecting all locations (not taking into account elevation) that share a given latitude . A location's position along a circle of latitude is given by its longitude . Circles of latitude are often called parallels because they are parallel to each other. On some map projections, including the Equirectangular projection , they are drawn at equidistant intervals. Circles of latitude become smaller the farther they are from the equator and the closer they are to the poles . A circle of latitude is perpendicular to all meridians at the points of intersection, and is hence a special case of a loxodrome . Contrary to what might be assumed from their straight-line representation on some map projections, a circle of latitude is not, with the sole exception of the Equator, the shortest distance between two points lying on the Earth. In other words, circles of latitude (except for the Equator) are not great circles (see also great-circle distance ). It is for this reason that an airplane traveling between a European and North American city that share the same latitude will fly farther north, over Greenland for example. Arcs of circles of latitude are sometimes used as boundaries between countries or regions where distinctive natural borders are lacking (such as in deserts), or when an artificial border is drawn as a "line on a map", as happened in Korea . Longitude (λ) Lines of longitude appear vertical with varying curvature in this projection; but are actually halves of great ellipses, with identical radii at a given latitude.
    [Show full text]
  • Latitude and Longitude
    Latitude and Longitude Finding your location throughout the world! What is Latitude? • Latitude is defined as a measurement of distance in degrees north and south of the equator • The word latitude is derived from the Latin word, “latus”, meaning “wide.” What is Latitude • There are 90 degrees of latitude from the equator to each of the poles, north and south. • Latitude lines are parallel, that is they are the same distance apart • These lines are sometimes refered to as parallels. The Equator • The equator is the longest of all lines of latitude • It divides the earth in half and is measured as 0° (Zero degrees). North and South Latitudes • Positions on latitude lines above the equator are called “north” and are in the northern hemisphere. • Positions on latitude lines below the equator are called “south” and are in the southern hemisphere. Let’s take a quiz Pull out your white boards Lines of latitude are ______________Parallel to the equator There are __________90 degrees of latitude north and south of the equator. The equator is ___________0 degrees. Another name for latitude lines is ______________.Parallels The equator divides the earth into ___________2 equal parts. Great Job!!! Lets Continue! What is Longitude? • Longitude is defined as measurement of distance in degrees east or west of the prime meridian. • The word longitude is derived from the Latin word, “longus”, meaning “length.” What is Longitude? • The Prime Meridian, as do all other lines of longitude, pass through the north and south pole. • They make the earth look like a peeled orange. The Prime Meridian • The Prime meridian divides the earth in half too.
    [Show full text]
  • PRIME MERIDIAN a Place Is
    Lines of Latitude and Longitude help us to answer a key geographical question: “Where am I?” What are Lines of Latitude and Longitude? Lines of Latitude and Longitude refer to the grid system of imaginary lines you will find on a map or globe. PARALLELS of Latitude and MERIDIANS of Longitude form an invisible grid over the earth’s surface and assist in pinpointing any location on Earth with great accuracy; everywhere has its own unique grid location, and this is expressed in terms of LATITUDE and LONGITUDE COORDINATES. Lines of LATITUDE are the ‘horizontal’ lines. They tell us whether a place is located in the NORTHERN or the SOUTHERN HEMISPHERE as well as how far North or South from the EQUATOR it is. Lines of LONGITUDE are the ‘vertical’ lines. They indicate how far East or West of the PRIME MERIDIAN a place is. • The EQUATOR is the 0° LATITUDE LINE. o North of the EQUATOR is the NORTHERN HEMISPHERE. o South of the EQUATOR is the SOUTHERN HEMISPHERE. • Lines of Latitude cross the PRIME MERIDIAN (longitude line) at right angles (90°). • Lines of Latitude circle the globe/world in an east- west direction. • Lines of Latitude are also known as PARALLELS. o As they are parallel to the Equator and apart always at the same distance. • Lines of Latitude measure distance north or south from the equator i.e. how far north or south a point lies from the Equator. • The distance between degree lines is about 69 miles (or about 110km). o A DEGREE (°) equals 60 minutes - 60’.
    [Show full text]
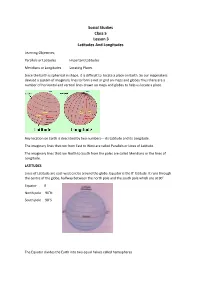
  • Social Studies Class 5 Lesson 3 Latitudes and Longitudes
    Social Studies Class 5 Lesson 3 Latitudes And Longitudes Learning Objectives; Parallels or Latitudes Important Latitudes Meridians or Longitudes Locating Places Since the Earth is spherical in shape, it is difficult to locate a place on Earth. So our mapmakers devised a system of imaginary lines to form a net or grid on maps and globes Thus there are a number of horizontal and vertical lines drawn on maps and globes to help us locate a place. Any location on Earth is described by two numbers--- its Latitude and its Longitude. The imaginary lines that run from East to West are called Parallels or Lines of Latitude. The imaginary lines that run North to South from the poles are called Meridians or the lines of Longitude. LATITUDES Lines of Latitude are east-west circles around the globe. Equator is the 0˚ latitude. It runs through the centre of the globe, halfway between the north pole and the south pole which are at 90˚. Equator 0 North pole 90˚N South pole 90˚S The Equator divides the Earth into two equal halves called hemispheres. 1. Northern Hemisphere: The upper half of the Earth to the north of the equator is called Northern Hemisphere. 2. Southern Hemisphere:The lower half of the earth to the south of the equator is called Southern Hemisphere. Features of Latitude These lines run parallel to each other. They are located at an equal distance from each other. They are also called Parallels. All Parallels form a complete circle around the globe. North Pole and South Pole are however shown as points.
    [Show full text]
  • Maps and Globes
    Maps and Globes By Kennedy’s Korner Table of Contents Words to Know What are Maps and Globes Map Key or Symbols Cardinal Directions Intermediate Directions Equator Prime Meridian Hemispheres Coordinate Map Map scales Continents & Oceans Types of Maps Quick Check Review pages Extra Maps Quiz Words to Know compass rose- A circle showing the principal directions printed on a map or chart. Continent- Any of the world's main continuous expanses of land (Africa, Antarctica, Asia, Australia, Europe, North America, South America). equator - An imaginary line drawn around the earth equally distant from both poles, dividing the earth into northern and southern hemispheres globe - a spherical representation of earth. hemisphere- A half of the earth, usually as divided into northern and southern halves by the equator, or into western and eastern halves by the Prime Meridian. latitude- is the angular distance of any object from the equator measured in degrees. longitude- is the angular distance east or west on the earth's surface, measured by the angle contained between the meridian of a particular place. map - A diagrammatic representation of an area of land or sea showing physical features, cities, roads or other features. meridian- A circle of constant longitude passing through a given place on the earth's surface and the terrestrial poles. parallel- Side by side and having the same distance continuously between them. Poles - Either of the two locations (North Pole or South Pole) on the surface of the earth. Prime Meridian- The zero meridian (0°), used as a reference line from which longitude east and west is measured.
    [Show full text]
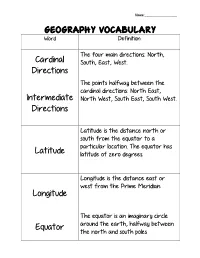
  • Cardinal Directions Intermediate Directions Latitude Longitude Equator
    Name:_________________ GEOGRAPHY VOCABULARY Word Definition The four main directions: North, Cardinal South, East, West. Directions The points halfway between the cardinal directions: North East, Intermediate North West, South East, South West. Directions Latitude is the distance north or south from the equator to a particular location. The equator has Latitude latitude of zero degrees. Longitude is the distance east or west from the Prime Meridian. Longitude The equator is an imaginary circle Equator around the earth, halfway between the north and south poles Name:_________________ The prime meridian (0 degrees Prime longitude) is the meridian that passes Meridian through Greenwich, England. The legend of a map (also called the Map Legend key) is a small table accompanying the map that explains the symbols that or Key are used on the map. A landmass on Earth. The seven continents are Africa, Antarctica, Asia, Australia, Europe, North Continent America, and South America. A half of the earth. The earth has Hemisphere 4 hemispheres: North, South, East, and West. Name:_________________ For the first globe, have your student draw in the equator and lines of latitude. Then shade the northern hemisphere one color and the southern half a different color. For the second globe, have the students draw the prime meridian and lines of longitude. Have them shade the eastern half of the globe one color and the western half a different color. Have the students match the vocabulary terms. .
    [Show full text]
  • Latitude & Longitude Review
    Latitude & Longitude Introduction Latitude Lines of Latitude are also called parallels because they are parallel to each other. They NEVER touch. The 0° Latitude line is called the Equator. They measure distance north and south of the Equator How to remember? Longitude Lines of Longitude are also called meridians. The 0° Longitude line is called the Prime Meridian. It runs through Greenwich England They measure distance east and west of the Prime Meridian until it gets to 180° How to remember? Hemispheres The Prime Meridian divides the earth in half into the Eastern and Western Hemispheres. Hemispheres The Equator divides the earth in half into the Northern and Southern Hemispheres. .When giving the absolute location of a place you first say the Latitude followed by the Longitude. .Boise is located at 44 N., 116W .Both Latitude and Longitude are measured in degrees. .Always make sure you are in the correct hemisphere: North or South – East or West. Latitude and Longitude Part 2 66 ½° N Arctic Circle 23 ½° N Tropic of Cancer Equator 23 ½° S Tropic of Capricorn 66 ½° S Antarctic Circle Prime Meridian Things To Remember • You always read or say the Latitude 1st then the Longitude (makes sense – it is alphabetical. ) – (30°N, 108°W) • Use your pointer finger on both hands to follow each line. • Don’t get hung up on 1 or 2 degrees. • Latitude and Longitude lines are the GRID on the map – smaller area maps may use a different grid. 1. Find 20°N & 100°W – Put a Dot & label 1 2. Find 20°S & 140°E – Put a Dot & label 2 3.
    [Show full text]