DOCSLIB.ORG

The Influence of Cochlear Shape on Low-Frequency Hearing

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Influence of Cochlear Shape on Low-Frequency Hearing The influence of cochlear shape on low-frequency hearing Daphne Manoussaki*†, Richard S. Chadwick‡§, Darlene R. Ketten‡¶ʈ, Julie Arrudaʈ**, Emilios K. Dimitriadis††, and Jen T. O’Malley** *Department of Mathematics, Vanderbilt University, Nashville, TN 37240; †Department of Sciences, Technical University of Crete, Hania, Greece 73100; ‡Auditory Mechanics Section, National Institute on Deafness and Other Communication Disorders, and ††Laboratory of Bioengineering and Physical Science, National Institute of Biomedical Imaging and Bioengineering, National Institutes of Health, Bethesda, MD 20892; ¶Department of Otology and Laryngology, Harvard Medical School, Boston, MA 02114; ʈWoods Hole Oceanographic Institution, Woods Hole, MA 02543; and **Massachusetts Ear and Eye Infirmary, Boston, MA 02114 Edited by Jon H. Kaas, Vanderbilt University, Nashville, TN, and approved February 13, 2008 (received for review October 22, 2007) The conventional theory about the snail shell shape of the mam- radius of curvature at the apex as a single, simple measure of malian cochlea is that it evolved essentially and perhaps solely to curvature change (and thus, energy redistribution), and show conserve space inside the skull. Recently, a theory proposed that that it is a robust correlate of LF hearing limits for both land and the spiral‘s graded curvature enhances the cochlea’s mechanical aquatic mammals. Contrary to the existing literature that has response to low frequencies. This article provides a multispecies suggested that material properties and geometry local to the LF analysis of cochlear shape to test this theory and demonstrates region control the LF limit (10, 11), we suggest that this measure that the ratio of the radii of curvature from the outermost and of curvature change of the entire cochlea affects the LF limit. innermost turns of the cochlear spiral is a significant cochlear To understand the effect of change of curvature, one must feature that correlates strongly with low-frequency hearing limits. look at how the cochlea functions. Incoming sounds are trans- The ratio, which is a measure of curvature gradient, is a reflection mitted to cochlear fluids by the eardrum (tympanic membrane) of the ability of cochlear curvature to focus acoustic energy at the and three small articulated bones (the ossicles) that connect the outer wall of the cochlear canal as the wave propagates toward the tympanic membrane to a second membrane (oval window) apex of the cochlea. sealing one of the three chambers of the fluid-filled cochlear spiral. The resulting pressure oscillations in the cochlear fluids inner ear ͉ function ͉ mammalian evolution ͉ spiral deflect the basilar membrane (BM), a membranous partition that forms one boundary of the central chamber (scala media) t is often thought that mammalian cochleae are coiled to pack and spans the length of the spiral cochlea. This deflection Ia longer organ into a small space inside the skull and that the propagates along the BM from the oval window toward the spiral cochlear coil increases the efficiency of blood and nerve supply apex as a transverse traveling wave with a time-varying peak through a central shaft (1). Although these spatial advantages of displacement envelope. At high frequencies, the amplitude of a coiled cochlea have been generally accepted, understanding the traveling wave is maximized near the cochlear base where the the effect of shape on hearing itself has been a challenge. BM is stiffest. The traveling wave is effectively terminated Cochlear coiling is absent in reptiles, birds, and monotreme shortly thereafter. At LFs, the wave travels the full length of the mammals, and it appears to have originated in the marsupial and spiral and achieves its maximum amplitude near the spiral’s apex placental mammal lines (2). Coiling allowed the cochlea to where the BM is more compliant (12). The mechanical proper- become longer, increasing the potential octave range, whereas ties of the BM as well as the energy density traveling along the uncoiled cochleae have been associated with relatively limited cochlea control the characteristics of motion of the traveling hearing ranges. Earlier studies suggested that the evolution of wave. coiling enhanced high-frequency hearing (3). This suggestion, However, both the peak amplitude of the traveling wave and however, is not wholly satisfactory for several reasons. Above all, the radial profile of the transverse wave are important. Neuro- increased hearing ranges extended both high-frequency and sensory hair cells seated atop the BM are stimulated by radial low-frequency (LF) hearing abilities in mammals compared with shear forces. Hair cells are therefore responsive to radial vari- birds and reptiles and improved sensitivities compared with even ations in BM motion. We thus suggest that the spiral shape LF specialist fishes (4). Further, the highest-frequency waves are affects strongly these radial motion variations, and by doing so, resolved near the base (entrance) before they propagate far it also affects hair cell stimulation and hearing. enough into the spiral to ‘‘feel’’ the cochlear curvature; it is the lowest-frequency waves that propagate along the cochlea’s coils. Calculation of Sound Energy Focusing at the Apex Earlier work on land mammal ear anatomy (5) found a strong The radial profile of the BM wave is a result of the wave energy correlation between the LF hearing limit of each species and the distribution across the cochlear channel. As wave energy prop- product of basilar membrane length and number of spiral turns, agates along the spiral, energy propagation paths glance off a but did not adduce a mechanistic explanation for this relation- wall with increasing curvature, and thus progressively focus ship. Other data suggested also that longitudinal curvature of the toward the outer wall (8). The energy propagation pathways are cochlear duct generates radial fluid pressure gradients (6) and enhances radial movement of hair cells (1, 7). Recently, a new theory proposed that the cochlea’s graded Author contributions: D.M. and R.S.C. designed research; D.M., R.S.C., D.R.K., J.A., and curvature actually enhances LF hearing (8), similar to a whis- J.T.O. performed research; D.M., R.S.C., and E.K.D. contributed new reagents/analytic tools; pering gallery in which sounds cling to the concave surface of the D.M., R.S.C., D.R.K., J.A., and J.T.O. analyzed data; and D.M., R.S.C., and D.R.K. wrote the lateral wall (9). The cochlear spiral shape redistributes wave paper. energy toward the outer wall, particularly along its innermost, The authors declare no conflict of interest. tightest, apical turn, and thereby enhances sensitivity to lower- This article is a PNAS Direct Submission. frequency sounds. Freely available online through the PNAS open access option. In this article, we test this theory morphometrically. We use §To whom correspondence should be addressed. E-mail: [email protected]. the ratio of the radius of curvature at the base of the spiral to the © 2008 by The National Academy of Sciences of the USA 6162–6166 ͉ PNAS ͉ April 22, 2008 ͉ vol. 105 ͉ no. 16 www.pnas.org͞cgi͞doi͞10.1073͞pnas.0710037105 Downloaded by guest on September 30, 2021 Fig. 1. Focusing of rays by spirals. A uniform distribution of 200 rays (red) entering and filling a spiral duct (walls in blue) at the largest radius is increasingly focused toward the outer wall as the rays progress toward the apex (spiral center). The effect increases with the parameter ␣, which controls the rate of decrease of radius in the exponential spirals described by the formula given in the figure. Insets shown below each spiral, in an expanded scale, indicate the radial gradient of ray or energy density at the apex. These distributions should be compared with a uniform distribution of rays entering at the largest radius to see the energy density focusing effect of the spiral walls. likened to sound propagation in a whispering gallery, only the This result assumes that waves propagate to the LF region. An cochlear spiral, because of this focusing, is more effective. estimate for the energy focusing at a position ␪ along the spiral Regardless of the mechanism for the encoding of the lower can thus be given by the ratio of energy difference at angular frequencies (phase locking or, as for higher frequencies, ampli- position ␪ to the energy difference at the cochlea base: tude-place mapping), changing energy density distribution along ⌬E͑␪͒ R w ͑␪͒2 the radial direction would change the radial profile of the Ϸ base ͩ ϩ bm ͪ ⌬ ͑␪͒ 1 ͑␪͒2 . [4] vibration of the different cochlear structures (7), affecting LF Ebase Rm 6 Rm hearing. In particular, energy density focusing at the outer wall increases the dynamic displacement ␩ ϭ ␩(r, ␪) of the BM The results in Eqs. 3 and 4, to leading order, do not depend on 4 normal to the resting position, and creates an effective radial tilt the wavelength. According to Eq. , energy focusing at an angular position ␪ along the spiral is inversely proportional to the T in the BM motion that is equal to the difference in displace- ratio of the corresponding radii of curvature. The ratio, and thus APPLIED ment ⌬␩ between inner and outer walls divided by BM width energy focusing, becomes greatest at the apex, where the ratio of MATHEMATICS w : bm the radius of curvature at the base to radius of curvature at the ⌬␩ 2 2 apex is greatest, and where low frequencies are resolved: wbm wbm T ϭ ϰ ͩ ϩ ͪ [1] ␭7/2 1 2 , 2 wbm Rm 10 R ⌬E w m apex Ϸ ␳ͩ ϩ bm ͪ ⌬ 1 2 , [5] Ebase 6 Rm where Rm is the radial position of the BM midline and ␭ is the apex wavelength of the associated longitudinal wave (8).
Load more

Recommended publications
  • Sound and the Ear Chapter 2
    © Jones & Bartlett Learning, LLC © Jones & Bartlett Learning, LLC NOT FOR SALE OR DISTRIBUTION NOT FOR SALE OR DISTRIBUTION Chapter© Jones & Bartlett 2 Learning, LLC © Jones & Bartlett Learning, LLC NOT FOR SALE OR DISTRIBUTION NOT FOR SALE OR DISTRIBUTION Sound and the Ear © Jones Karen &J. Kushla,Bartlett ScD, Learning, CCC-A, FAAA LLC © Jones & Bartlett Learning, LLC Lecturer NOT School FOR of SALE Communication OR DISTRIBUTION Disorders and Deafness NOT FOR SALE OR DISTRIBUTION Kean University © Jones & Bartlett Key Learning, Terms LLC © Jones & Bartlett Learning, LLC NOT FOR SALE OR Acceleration DISTRIBUTION Incus NOT FOR SALE OR Saccule DISTRIBUTION Acoustics Inertia Scala media Auditory labyrinth Inner hair cells Scala tympani Basilar membrane Linear scale Scala vestibuli Bel Logarithmic scale Semicircular canals Boyle’s law Malleus Sensorineural hearing loss Broca’s area © Jones & Bartlett Mass Learning, LLC Simple harmonic© Jones motion (SHM) & Bartlett Learning, LLC Brownian motion Membranous labyrinth Sound Cochlea NOT FOR SALE OR Mixed DISTRIBUTION hearing loss Stapedius muscleNOT FOR SALE OR DISTRIBUTION Compression Organ of Corti Stapes Condensation Osseous labyrinth Tectorial membrane Conductive hearing loss Ossicular chain Tensor tympani muscle Decibel (dB) Ossicles Tonotopic organization © Jones Decibel & hearing Bartlett level (dB Learning, HL) LLC Outer ear © Jones Transducer & Bartlett Learning, LLC Decibel sensation level (dB SL) Outer hair cells Traveling wave theory NOT Decibel FOR sound SALE pressure OR level DISTRIBUTION
    [Show full text]
  • The Standing Acoustic Wave Principle Within the Frequency Analysis Of
    inee Eng ring al & ic d M e e d Misun, J Biomed Eng Med Devic 2016, 1:3 m i o c i a B l D f o e v DOI: 10.4172/2475-7586.1000116 l i a c n e r s u o Journal of Biomedical Engineering and Medical Devices J ISSN: 2475-7586 Review Article Open Access The Standing Acoustic Wave Principle within the Frequency Analysis of Acoustic Signals in the Cochlea Vojtech Misun* Department of Solid Mechanics, Mechatronics and Biomechanics, Brno University of Technology, Brno, Czech Republic Abstract The organ of hearing is responsible for the correct frequency analysis of auditory perceptions coming from the outer environment. The article deals with the principles of the analysis of auditory perceptions in the cochlea only, i.e., from the overall signal leaving the oval window to its decomposition realized by the basilar membrane. The paper presents two different methods with the function of the cochlea considered as a frequency analyzer of perceived acoustic signals. First, there is an analysis of the principle that cochlear function involves acoustic waves travelling along the basilar membrane; this concept is one that prevails in the contemporary specialist literature. Then, a new principle with the working name “the principle of standing acoustic waves in the common cavity of the scala vestibuli and scala tympani” is presented and defined in depth. According to this principle, individual structural modes of the basilar membrane are excited by continuous standing waves of acoustic pressure in the scale tympani. Keywords: Cochlea function; Acoustic signals; Frequency analysis; The following is a description of the theories in question: Travelling wave principle; Standing wave principle 1.
    [Show full text]
  • Low-Frequency Noise: a Biophysical Phenomenon M
    PSC REF#:288480 Public Service Commission of Wisconsin RECEIVED: 07/08/16, 8:46:12 AM Congres Geluid, Trillingen, Luchtkwaliteit en Gebied & Gebouw 2012 Low-frequency noise: a biophysical phenomenon M. Oud (medical physicist / consultant)* * [email protected], http://nl.linkedin.com/in/mireilleoud, the Netherlands Abstract Complaints on low-frequency noise were till recently fairly unexplained, but audiological research shed light on the mechanisms that enable perception of frequencies below the threshold of average normal hearing. It was shown that exposure to low-frequency sound may alter the inner ear. This results in an increase of sensitivity to low-frequency sounds, and as a result, previously imperceptible sounds becomes audible to the exposed person. Interactions between inner-ear responses to low and higher frequencies furthermore account for perception of low-frequency sound, as well as the property of the hearing system to perceive so-called difference tones. Introduction A growing minority of people experiences an increased sensitivity for low-frequency sound. Not surprisingly, they complain about noise, even about loud noise in some cases. Their complaints about the presence of hum, buzz, and rumble are often not recognized as a nuisance, since the majority of people does not perceive the very low frequencies. Low-frequency noise (LFN) may have serious health effects like vertigo, disturbed sleep, stress, hypertension, and heart rhythm disorders [1]. The number of sufferers is growing, and this has two possible causes. The sources of low- frequency sounds increased in volume and dimension over the past decades, and auditory sensitisation takes years to develop. Nowadays, the main source of low-frequency noise is the public infrastructure: wind turbines, gas transmission grid, industrial plants, road and railway traffic, sewerage, and so on.
    [Show full text]
  • CONGENITAL MALFORMATIONS of the INNER EAR Malformaciones Congénitas Del Oído Interno
    topic review CONGENITAL MALFORMATIONS OF THE INNER EAR Malformaciones congénitas del oído interno. Revisión de tema Laura Vanessa Ramírez Pedroza1 Hernán Darío Cano Riaño2 Federico Guillermo Lubinus Badillo2 Summary Key words (MeSH) There are a great variety of congenital malformations that can affect the inner ear, Ear with a diversity of physiopathologies, involved altered structures and age of symptom Ear, inner onset. Therefore, it is important to know and identify these alterations opportunely Hearing loss Vestibule, labyrinth to lower the risks of all the complications, being of great importance, among others, Cochlea the alterations in language development and social interactions. Magnetic resonance imaging Resumen Existe una gran variedad de malformaciones congénitas que pueden afectar al Palabras clave (DeCS) oído interno, con distintas fisiopatologías, diferentes estructuras alteradas y edad Oído de aparición de los síntomas. Por lo anterior, es necesario conocer e identificar Oído interno dichas alteraciones, con el fin de actuar oportunamente y reducir el riesgo de las Pérdida auditiva Vestíbulo del laberinto complicaciones, entre otras —de gran importancia— las alteraciones en el área del Cóclea lenguaje y en el ámbito social. Imagen por resonancia magnética 1. Epidemiology • Hyperbilirubinemia Ear malformations occur in 1 in 10,000 or 20,000 • Respiratory distress from meconium aspiration cases (1). One in every 1,000 children has some degree • Craniofacial alterations (3) of sensorineural hearing impairment, with an average • Mechanical ventilation for more than five days age at diagnosis of 4.9 years. The prevalence of hearing • TORCH Syndrome (4) impairment in newborns with risk factors has been determined to be 9.52% (2).
    [Show full text]
  • ANATOMY of EAR Basic Ear Anatomy
    ANATOMY OF EAR Basic Ear Anatomy • Expected outcomes • To understand the hearing mechanism • To be able to identify the structures of the ear Development of Ear 1. Pinna develops from 1st & 2nd Branchial arch (Hillocks of His). Starts at 6 Weeks & is complete by 20 weeks. 2. E.A.M. develops from dorsal end of 1st branchial arch starting at 6-8 weeks and is complete by 28 weeks. 3. Middle Ear development —Malleus & Incus develop between 6-8 weeks from 1st & 2nd branchial arch. Branchial arches & Development of Ear Dev. contd---- • T.M at 28 weeks from all 3 germinal layers . • Foot plate of stapes develops from otic capsule b/w 6- 8 weeks. • Inner ear develops from otic capsule starting at 5 weeks & is complete by 25 weeks. • Development of external/middle/inner ear is independent of each other. Development of ear External Ear • It consists of - Pinna and External auditory meatus. Pinna • It is made up of fibro elastic cartilage covered by skin and connected to the surrounding parts by ligaments and muscles. • Various landmarks on the pinna are helix, antihelix, lobule, tragus, concha, scaphoid fossa and triangular fossa • Pinna has two surfaces i.e. medial or cranial surface and a lateral surface . • Cymba concha lies between crus helix and crus antihelix. It is an important landmark for mastoid antrum. Anatomy of external ear • Landmarks of pinna Anatomy of external ear • Bat-Ear is the most common congenital anomaly of pinna in which antihelix has not developed and excessive conchal cartilage is present. • Corrections of Pinna defects are done at 6 years of age.
    [Show full text]
  • Organum Vestibulocochleare INTERNAL EAR MIDDLE EAR EXTERNAL EAR PETROSAL BONE- Eq EXTERNAL EAR AURICLE
    EAR organum vestibulocochleare INTERNAL EAR MIDDLE EAR EXTERNAL EAR PETROSAL BONE- Eq EXTERNAL EAR AURICLE The external ear plays the role of an acoustic antenna: auricle the auricle (together with the head) collects and focuses sound waves, the ear canal act as a resonator. tympanic membrane anular cartilage meatus acusticus externus EXTERNAL EAR EXTERNAL EAR AURICLE scutiform cartilage Auricular muscles: -Dorsal -Ventral -Rostral -Caudal EXTERNAL EAR MEATUS ACUSTICUS EXTERNUS auricular cartilage vertical canal auditory ossicles horizontal cochlea canal auditory tube tympanic tympanic eardrum bulla cavity tympanic membrane MIDDLE EAR Auditory ossicles STAPES INCUS Tympanic cavity: (anvil) (stirrup) - epitympanium - mesotympanium - hypotympanium MALLEUS (hammer) auditory vestibular window- ossicles or oval window through which mechanical stimuli (transmitted by the auditory ossicles) enter the epitympanic internal ear for translation recess into nerve impulses auditory tube (Eustachian tube) cochlear window- or round window tympanic cavity bulla tympanica through which the vibration of the perilympha is absorbed MIDDLE EAR MIDDLE EAR GUTTURAL POUCH- Eq MIDDLE EAR AUDITORY OSSICLES head INCUS processus rostralis (stirrup) STAPES processus muscularis (anvil) manubrium short crus body MALLEUS (hammer) Two muscles of the ossicles: long crus m. tensor tympani- n. tensoris tympani ex. n. base mandibularis (footplate) m. stapedius- n. stapedius ex. n. facialis crus The muscles fix the bones and protect the cochlea crus against the harmful effects
    [Show full text]
  • The Special Senses the Ear External Ear Middle
    1/24/2016 The Ear • The organ of hearing and equilibrium – Cranial nerve VIII - Vestibulocochlear – Regions The Special Senses • External ear • Middle ear Hearing and • Internal ear (labyrinth) Equilibrium External Ear Middle Internal ear • Two parts External ear (labyrinth) ear – Pinna or auricle (external structures) – External auditory meatus (car canal) Auricle • Site of cerumen (earwax) production (pinna) – Waterproofing, protection • Separated from the middle ear by the tympanic membrane Helix (eardrum) – Vibrates in response to sound waves Lobule External acoustic Tympanic Pharyngotympanic meatus membrane (auditory) tube (a) The three regions of the ear Figure 15.25a Middle Ear Epitympanic Middle Ear Superior Malleus Incus recess Lateral • Tympanic cavity Anterior – Air-filled chamber – Openings View • Tympanic membrane – covers opening to outer ear • Round and oval windows – openings to inner ear • Epitympanic recess – dead-end cavity into temporal bone of unknown function • Auditory tube – AKA Eustachian tube or pharyngotympanic tube Pharyngotym- panic tube Tensor Tympanic Stapes Stapedius tympani membrane muscle muscle (medial view) Figure 15.26 1 1/24/2016 Middle Ear Middle Ear • Auditory tube (Eustachian tube) • Otitis Media – Connects the middle ear to the nasopharynx • Equalizes pressure – Opens during swallowing and yawning Middle Ear Middle Ear • Contains auditory ossicles (bones) • Sound waves cause tympanic membrane to vibrate – Malleus • Ossicles help transmit vibrations into the inner ear – Incus – Reduce the area
    [Show full text]
  • Turbulence Around the Otoliths Sappey's Hostility and Br
    B-ENT, 2006, 2, 99-102 A Historical Vignette “Be proud of yourself: you have a History!” Turbulence around the otoliths Sappey’s hostility and Breschet’s defence J. Tainmont W. Churchill Avenue 172, 1180 Brussels, Belgium Key-words. Vestibular apparatus; otoliths; Breschet; Sappey; history of otology Abstract. Turbulence around the otoliths. Sappey’s hostility and Breschet’s defence. Nowadays, the animosity between medical scholars is seldom apparent. However, during the XIXth century it was not necessarily so. We find an example of this in Sappey’s hostility against his colleague anatomist Gilbert Breschet. It concerned the discovery of the otoliths of the inner ear that Breschet attributed to himself. We present here Breschet’s defence. Sappey’s hostility (Figure 1) Marie-Philibert-Constant Sappey was a French anatomist who received from the 1900 Larousse Encyclopaedia the honour of an article with a pen-and-ink draw- ing. He was born at Bourg (Ain department) in 1810 and he died in Paris in 1896. He published important works concerning the lymphatic vessels. He described their anatomy, physiology, pathol- ogy and iconography. We owe him the knowledge of the lymphatic vessels and nodes of the supra- glottic part of the larynx (1889) AB that was the basis of the radical neck dissection for laryngeal can- Figure 1 cer. Nevertheless, Sappey was also A. Sappey (1810-1896). B. Lymphatic vessels of head and neck with the great lymphatic vein1. an irascible man! In his treatise on descriptive anatomy (1845-1863), in the chapter “sense of hearing”, we find a history of the discovery “After the work of Scarpa, was very simple, to mention it was of the membranous labyrinth into Breschet’s one appeared… In that enough.
    [Show full text]
  • The Special Senses
    HOMEWORK DUE IN LAB 5 HW page 9: Matching Eye Disorders PreLab 5 THE SPECIAL SENSES Hearing and Equilibrium THE EAR The organ of hearing and equilibrium . Cranial nerve VIII - Vestibulocochlear . Regions . External ear . Middle ear . Internal ear (labyrinth) Middle Internal ear External ear (labyrinth) ear Auricle (pinna) Helix Lobule External acoustic Tympanic Pharyngotympanic meatus membrane (auditory) tube (a) The three regions of the ear Figure 15.25a Middle Ear Epitympanic Superior Malleus Incus recess Lateral Anterior View Pharyngotym- panic tube Tensor Tympanic Stapes Stapedius tympani membrane muscle muscle (medial view) Copyright © 2010 Pearson Education, Inc. Figure 15.26 MIDDLE EAR Auditory tube . Connects the middle ear to the nasopharynx . Equalizes pressure . Opens during swallowing and yawning . Otitis media INNER EAR Contains functional organs for hearing & equilibrium . Bony labyrinth . Membranous labyrinth Superior vestibular ganglion Inferior vestibular ganglion Temporal bone Semicircular ducts in Facial nerve semicircular canals Vestibular nerve Anterior Posterior Lateral Cochlear Cristae ampullares nerve in the membranous Maculae ampullae Spiral organ Utricle in (of Corti) vestibule Cochlear duct Saccule in in cochlea vestibule Stapes in Round oval window window Figure 15.27 INNER EAR - BONY LABYRINTH Three distinct regions . Vestibule . Gravity . Head position . Linear acceleration and deceleration . Semicircular canals . Angular acceleration and deceleration . Cochlea . Vibration Superior vestibular ganglion Inferior vestibular ganglion Temporal bone Semicircular ducts in Facial nerve semicircular canals Vestibular nerve Anterior Posterior Lateral Cochlear Cristae ampullares nerve in the membranous Maculae ampullae Spiral organ Utricle in (of Corti) vestibule Cochlear duct Saccule in in cochlea vestibule Stapes in Round oval window window Figure 15.27 INNER EAR The cochlea .
    [Show full text]
  • Tympanic Membrane (Membrana Tympanica, Myrinx)
    Auditory and vestibular system Auris, is = Us, oton Auditory and vestibular system • external ear (auris externa) • middle ear (auris media) • internal ear (auris interna) = organum vestibulo- cochleare External ear (Auris externa) • auricle (auricula, pinna) – elastic cartilage • external acoustic meatus (meatus acusticus externus) • tympanic membrane (membrana tympanica, myrinx) • helix Auricle – crus, spina, cauda – (tuberculum auriculare Darwini, apex auriculae) • antihelix – crura, fossa triangularis • scapha • concha auriculae – cymba, cavitas • tragus • antitragus • incisura intertragica • lobulus auriculae posterior surface = negative image of the anterior one ligaments: lig. auriculare ant., sup., post. muscles – innervation: n. facialis • extrinsic muscles = facial muscles – mm. auriculares (ant., sup., post.) – m. temporoparietalis • intrinsic muscles: rudimentary – m. tragicus + antitragicus – m. helicis major+minor – m. obliquus + transversus auriculae, m. pyramidalis auriculae cartilage: cartilago auriculae - elastic skin: dorsally more loosen, ventrally firmly fixed to perichondrium - othematoma Auricle – supply • arteries: a. temporalis superficialis → rr. auriculares ant. a. carotis externa → a. auricularis post. • veins: v. jugularis ext. • lymph: nn.ll. parotidei, mastoidei • nerves: sensory – nn. auriculares ant. from n. auriculotemporalis (ventrocranial 2/3) – r. auricularis n. X. (concha) – n. occipitalis minor (dosrocranial) – n. auricularis magnus (cudal) motor: n. VII. External acoustic meatus (meatus acusticus
    [Show full text]
  • 16.400 Human Factors Engineering, Lecture 6 Notes
    Spatial Disorientation 16.400/16.453 Human Factors Engineering Prof. L. Young Sept. 2011 1 SPATIAL DISORIENTATION IN FLIGHT Formal Definition “[A failure] to sense correctly the position, motion or attitude of his aircraft or of himself [herself] within the fixed coordinate system provided by the surface of the earth and the gravitational vertical. In addition, errors in perception by the aviator of his position, motion or attitude with respect to his aircraft, or of his own aircraft relative to other aircraft, may also be embraced within a broader definition of spatial disorientation in flight. -- Alan Benson (1978) 2 SPATIAL DISORIENTATION IN FLIGHT Spatial Disorientation Types TYPE I -- Unrecognized • Pilot Does Not Consciously Perceive Any Manifestation of Spatial Disorientation • Most Often Occurs When Pilot Breaks Instrument Cross-Check • Most Likely to Lead to Controlled Flight Into Terrain 3 SPATIAL DISORIENTATION IN FLIGHT Spatial Disorientation Types TYPE II -- Recognized • Pilot Consciously Perceives A Manifestation of Spatial Disorientation but May Not Attribute It to SD Itself • Conflict between “Natural” and “Synthetic” SD Percepts May Occur • Instrument Malfunction Is Often Suspected 4 SPATIAL DISORIENTATION IN FLIGHT Spatial Disorientation Types TYPE III -- Incapacitating • Experienced by 10-15% of Aviators • Vestibulo-Ocular Disorganization (i.e., uncontrollable nystagmus) • Motor Conflict (e.g., “Giant Hand”) • Temporal Distortion • Dissociation (“Break-Off”) 5 SPATIAL DISORIENTATION IN FLIGHT Predisposing Perceptual
    [Show full text]
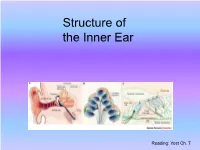
  • Structure of the Inner Ear
    Structure of the Inner Ear Reading: Yost Ch. 7 The Mammalian Ear The Inner Ear Inner ear contains two sensory structures in one organ: • Vestibular apparatus, which contains mechanosensory organs for balance (orientation re gravity), head acceleration in three dimensions. • Cochlea, which contains the mechanosensory epithelium for hearing (“Organ of Corti”). Vestibular and cochlear output fibers gather to become the VIIIth cranial nerve (vestibulocochlear). The Cochlea Transduction: Transmission: • Cochlea biomechanically segregates • Auditory hair cell receptors activate sound frequencies along the basilar auditory nerve fibers (ANFs). membrane • ANFs encode information about the • Basilar membrane creates a “filter frequency, amplitude, and timing of bank” of auditory receptors (“hair the acoustic stimulus, and relay that cells”), which convert sound energy encoded information to the central into neurophysiological responses. auditory system. Human Cochlea A bony, three-chambered tubular Apex structure. Coiled into a 2.5-turn helix, 35 mm long (human) from base (stapes/oval window) to apex. Central axis of helix is refered to as the modiolus (mō-dī´-ō-lus). The cell bodies of spiral ganglion cells (auditory nerve Base fibers) are located in the modiolus. Basilar membrane (BM; “cochlear partition”) extends along entire length Basilar Oval membrane Organ of Corti (sensory epithelium) window rests on the BM. Stapes Round window The Vestibule Oval window membrane attached to stapes, faces into the vestibule. The bony labyrinth is the rigid outer wall of the inner ear. It consists of three parts: the vestibule, semicircular canals and cochlea. They contain a clear fluid (brown), called the perilymph, in which floats the membranous labyrinth (blue).
    [Show full text]