The Shapes and Sizes of Two Domains of Tropomodulin, the P-End-Capping Protein of Actin-Tropomyosin
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
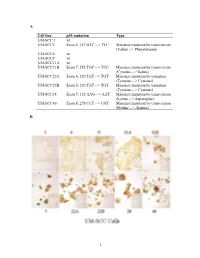
A Cell Line P53 Mutation Type UM
A Cell line p53 mutation Type UM-SCC 1 wt UM-SCC5 Exon 5, 157 GTC --> TTC Missense mutation by transversion (Valine --> Phenylalanine UM-SCC6 wt UM-SCC9 wt UM-SCC11A wt UM-SCC11B Exon 7, 242 TGC --> TCC Missense mutation by transversion (Cysteine --> Serine) UM-SCC22A Exon 6, 220 TAT --> TGT Missense mutation by transition (Tyrosine --> Cysteine) UM-SCC22B Exon 6, 220 TAT --> TGT Missense mutation by transition (Tyrosine --> Cysteine) UM-SCC38 Exon 5, 132 AAG --> AAT Missense mutation by transversion (Lysine --> Asparagine) UM-SCC46 Exon 8, 278 CCT --> CGT Missense mutation by transversion (Proline --> Alanine) B 1 Supplementary Methods Cell Lines and Cell Culture A panel of ten established HNSCC cell lines from the University of Michigan series (UM-SCC) was obtained from Dr. T. E. Carey at the University of Michigan, Ann Arbor, MI. The UM-SCC cell lines were derived from eight patients with SCC of the upper aerodigestive tract (supplemental Table 1). Patient age at tumor diagnosis ranged from 37 to 72 years. The cell lines selected were obtained from patients with stage I-IV tumors, distributed among oral, pharyngeal and laryngeal sites. All the patients had aggressive disease, with early recurrence and death within two years of therapy. Cell lines established from single isolates of a patient specimen are designated by a numeric designation, and where isolates from two time points or anatomical sites were obtained, the designation includes an alphabetical suffix (i.e., "A" or "B"). The cell lines were maintained in Eagle's minimal essential media supplemented with 10% fetal bovine serum and penicillin/streptomycin. -

Mechanism of Action Through an IFN Type I-Independent Responses To
Downloaded from http://www.jimmunol.org/ by guest on September 25, 2021 is online at: average * The Journal of Immunology , 12 of which you can access for free at: 2012; 188:3088-3098; Prepublished online 20 from submission to initial decision 4 weeks from acceptance to publication February 2012; doi: 10.4049/jimmunol.1101764 http://www.jimmunol.org/content/188/7/3088 MF59 and Pam3CSK4 Boost Adaptive Responses to Influenza Subunit Vaccine through an IFN Type I-Independent Mechanism of Action Elena Caproni, Elaine Tritto, Mario Cortese, Alessandro Muzzi, Flaviana Mosca, Elisabetta Monaci, Barbara Baudner, Anja Seubert and Ennio De Gregorio J Immunol cites 33 articles Submit online. Every submission reviewed by practicing scientists ? is published twice each month by Submit copyright permission requests at: http://www.aai.org/About/Publications/JI/copyright.html Receive free email-alerts when new articles cite this article. Sign up at: http://jimmunol.org/alerts http://jimmunol.org/subscription http://www.jimmunol.org/content/suppl/2012/02/21/jimmunol.110176 4.DC1 This article http://www.jimmunol.org/content/188/7/3088.full#ref-list-1 Information about subscribing to The JI No Triage! Fast Publication! Rapid Reviews! 30 days* Why • • • Material References Permissions Email Alerts Subscription Supplementary The Journal of Immunology The American Association of Immunologists, Inc., 1451 Rockville Pike, Suite 650, Rockville, MD 20852 Copyright © 2012 by The American Association of Immunologists, Inc. All rights reserved. Print ISSN: 0022-1767 -

Tropomodulin Isoform-Specific Regulation of Dendrite Development and Synapse Formation
This Accepted Manuscript has not been copyedited and formatted. The final version may differ from this version. Research Articles: Cellular/Molecular Tropomodulin Isoform-Specific Regulation of Dendrite Development and Synapse Formation Omotola F. Omotade1,3, Yanfang Rui1,3, Wenliang Lei1,3, Kuai Yu1, H. Criss Hartzell1, Velia M. Fowler4 and James Q. Zheng1,2,3 1Department of Cell Biology, Emory University School of Medicine, Atlanta, GA 30322. 2Department of Neurology 3Center for Neurodegenerative Diseases, Emory University School of Medicine, Atlanta, GA 30322. 4Department of Molecular Medicine, Scripps Research Institute, La Jolla, CA 92037 DOI: 10.1523/JNEUROSCI.3325-17.2018 Received: 22 November 2017 Revised: 25 September 2018 Accepted: 2 October 2018 Published: 9 October 2018 Author contributions: O.F.O. and J.Q.Z. designed research; O.F.O., Y.R., W.L., and K.Y. performed research; O.F.O. and J.Q.Z. analyzed data; O.F.O. and J.Q.Z. wrote the paper; Y.R., H.C.H., V.M.F., and J.Q.Z. edited the paper; V.M.F. contributed unpublished reagents/analytic tools. Conflict of Interest: The authors declare no competing financial interests. This research project was supported in part by research grants from National Institutes of Health to JQZ (GM083889, MH104632, and MH108025), OFO (5F31NS092437-03), VMF (EY017724) and HCH (EY014852, AR067786), as well as by the Emory University Integrated Cellular Imaging Microscopy Core of the Emory Neuroscience NINDS Core Facilities grant (5P30NS055077). We would like to thank Dr. Kenneth Myers for his technical expertise and help throughout the project. We also thank Drs. -

Serum Albumin OS=Homo Sapiens
Protein Name Cluster of Glial fibrillary acidic protein OS=Homo sapiens GN=GFAP PE=1 SV=1 (P14136) Serum albumin OS=Homo sapiens GN=ALB PE=1 SV=2 Cluster of Isoform 3 of Plectin OS=Homo sapiens GN=PLEC (Q15149-3) Cluster of Hemoglobin subunit beta OS=Homo sapiens GN=HBB PE=1 SV=2 (P68871) Vimentin OS=Homo sapiens GN=VIM PE=1 SV=4 Cluster of Tubulin beta-3 chain OS=Homo sapiens GN=TUBB3 PE=1 SV=2 (Q13509) Cluster of Actin, cytoplasmic 1 OS=Homo sapiens GN=ACTB PE=1 SV=1 (P60709) Cluster of Tubulin alpha-1B chain OS=Homo sapiens GN=TUBA1B PE=1 SV=1 (P68363) Cluster of Isoform 2 of Spectrin alpha chain, non-erythrocytic 1 OS=Homo sapiens GN=SPTAN1 (Q13813-2) Hemoglobin subunit alpha OS=Homo sapiens GN=HBA1 PE=1 SV=2 Cluster of Spectrin beta chain, non-erythrocytic 1 OS=Homo sapiens GN=SPTBN1 PE=1 SV=2 (Q01082) Cluster of Pyruvate kinase isozymes M1/M2 OS=Homo sapiens GN=PKM PE=1 SV=4 (P14618) Glyceraldehyde-3-phosphate dehydrogenase OS=Homo sapiens GN=GAPDH PE=1 SV=3 Clathrin heavy chain 1 OS=Homo sapiens GN=CLTC PE=1 SV=5 Filamin-A OS=Homo sapiens GN=FLNA PE=1 SV=4 Cytoplasmic dynein 1 heavy chain 1 OS=Homo sapiens GN=DYNC1H1 PE=1 SV=5 Cluster of ATPase, Na+/K+ transporting, alpha 2 (+) polypeptide OS=Homo sapiens GN=ATP1A2 PE=3 SV=1 (B1AKY9) Fibrinogen beta chain OS=Homo sapiens GN=FGB PE=1 SV=2 Fibrinogen alpha chain OS=Homo sapiens GN=FGA PE=1 SV=2 Dihydropyrimidinase-related protein 2 OS=Homo sapiens GN=DPYSL2 PE=1 SV=1 Cluster of Alpha-actinin-1 OS=Homo sapiens GN=ACTN1 PE=1 SV=2 (P12814) 60 kDa heat shock protein, mitochondrial OS=Homo -

IDENTIFICATION and CHARACTERIZATION of ACTIN-REGULATORY PROTEINS in the HAIR CELL's CUTICULAR PLATE by LANA MARY POLLOCK Subm
IDENTIFICATION AND CHARACTERIZATION OF ACTIN-REGULATORY PROTEINS IN THE HAIR CELL’S CUTICULAR PLATE by LANA MARY POLLOCK Submitted in partial fulfilment of the requirements for the degree of Doctor of Philosophy Dissertation advisor: Brian M. McDermott Jr., Ph.D. Department of Genetics and Genome Sciences CASE WESTERN RESERVE UNIVERSITY January 2016 Case Western Reserve University School of Graduate Studies We, the thesis committee, hereby approve the thesis/dissertation of Lana Pollock, candidate for the degree of Doctor of Philosophy (PhD).* (signed)_________Zhenghe Wang, Ph.D._________________ (chair of committee) ___________Brian McDermott, Ph.D._______________ ___________ Hua Lou, Ph.D._____________________ ___________Stephen Maricich, Ph.D., M.D.___________ ___________Anthony Wynshaw-Boris, Ph.D., M.D._____ Date of defense_____September 8th, 2015_______________ *we also certify that written approval has been obtained for release of any proprietary material contained therein 2 This thesis is dedicated to Daniel Margevicius. Thank you for your unwavering love and support. Ačiū!! 3 Table of contents List of Tables ........................................................................................................ 7 List of Figures ....................................................................................................... 8 List of abbreviations ............................................................................................ 13 Abstract ............................................................................................................. -

Cytoskeletal Remodeling in Cancer
biology Review Cytoskeletal Remodeling in Cancer Jaya Aseervatham Department of Ophthalmology, University of Texas Health Science Center at Houston, Houston, TX 77054, USA; [email protected]; Tel.: +146-9767-0166 Received: 15 October 2020; Accepted: 4 November 2020; Published: 7 November 2020 Simple Summary: Cell migration is an essential process from embryogenesis to cell death. This is tightly regulated by numerous proteins that help in proper functioning of the cell. In diseases like cancer, this process is deregulated and helps in the dissemination of tumor cells from the primary site to secondary sites initiating the process of metastasis. For metastasis to be efficient, cytoskeletal components like actin, myosin, and intermediate filaments and their associated proteins should co-ordinate in an orderly fashion leading to the formation of many cellular protrusions-like lamellipodia and filopodia and invadopodia. Knowledge of this process is the key to control metastasis of cancer cells that leads to death in 90% of the patients. The focus of this review is giving an overall understanding of these process, concentrating on the changes in protein association and regulation and how the tumor cells use it to their advantage. Since the expression of cytoskeletal proteins can be directly related to the degree of malignancy, knowledge about these proteins will provide powerful tools to improve both cancer prognosis and treatment. Abstract: Successful metastasis depends on cell invasion, migration, host immune escape, extravasation, and angiogenesis. The process of cell invasion and migration relies on the dynamic changes taking place in the cytoskeletal components; actin, tubulin and intermediate filaments. This is possible due to the plasticity of the cytoskeleton and coordinated action of all the three, is crucial for the process of metastasis from the primary site. -

Actin and Tropomodulin Isoforms Link to the Sarcoplasmic Reticulum in Skeletal Muscle Fibers
JCB: Article Cytoplasmic -actin and tropomodulin isoforms link to the sarcoplasmic reticulum in skeletal muscle fibers David S. Gokhin and Velia M. Fowler Department of Cell Biology, The Scripps Research Institute, La Jolla, CA 92037 he sarcoplasmic reticulum (SR) serves as the contained an M line complex composed of small ankyrin 2+ Ca reservoir for muscle contraction. Tropomodu- 1.5 (sAnk1.5), cyto-actin, Tmod3, Tm4, and Tm5NM1. Tlins (Tmods) cap filamentous actin (F-actin) pointed Tmod1 deletion caused Tmod3 to leave its SR compart- ends, bind tropomyosins (Tms), and regulate F-actin ment, leading to mislocalization and destabilization of the organization. In this paper, we use a genetic targeting Tmod3–cyto-actin–sAnk1.5 complex. This was accompa- approach to examine the effect of Tmod1 deletion on the nied by SR morphological defects, impaired Ca2+ release, organization of cytoplasmic -actin (cyto-actin) in the SR and an age-dependent increase in sarcomere misalign- of skeletal muscle. In wild-type muscle fibers, cyto-actin ment. Thus, Tmod3 regulates SR-associated cyto-actin and Tmod3 defined an SR microdomain that was distinct architecture, mechanically stabilizes the SR via a novel from another Z line–flanking SR microdomain containing cytoskeletal linkage to sAnk1.5, and maintains the align- Tmod1 and Tmod4. The cyto-actin/Tmod3 microdomain ment of adjacent myofibrils. Introduction Striated muscle contraction is built on an exquisitely regulated Williams et al., 2001). cyto-Actin is dispensable for skeletal actin cytoskeleton, where actin isoforms sort into distinct, non- muscle development, but its absence can produce muscle weak- overlapping compartments. The thin filaments of sarcomeres ness, indicating that cyto-actin plays a role in muscle mechani- consist of skeletal muscle -actin (sk-actin), whereas extrasar- cal performance (Sonnemann et al., 2006; Belyantseva et al., comeric membrane compartments contain cytoplasmic -actin 2009). -

Protein T1 C1 Accession No. Description
Protein T1 C1 Accession No. Description SW:143B_HUMAN + + P31946 14-3-3 protein beta/alpha (protein kinase c inhibitor protein-1) (kcip-1) (protein 1054). 14-3-3 protein epsilon (mitochondrial import stimulation factor l subunit) (protein SW:143E_HUMAN + + P42655 P29360 Q63631 kinase c inhibitor protein-1) (kcip-1) (14-3-3e). SW:143S_HUMAN + - P31947 14-3-3 protein sigma (stratifin) (epithelial cell marker protein 1). SW:143T_HUMAN + - P27348 14-3-3 protein tau (14-3-3 protein theta) (14-3-3 protein t-cell) (hs1 protein). 14-3-3 protein zeta/delta (protein kinase c inhibitor protein-1) (kcip-1) (factor SW:143Z_HUMAN + + P29312 P29213 activating exoenzyme s) (fas). P01889 Q29638 Q29681 Q29854 Q29861 Q31613 hla class i histocompatibility antigen, b-7 alpha chain precursor (mhc class i antigen SW:1B07_HUMAN + - Q9GIX1 Q9TP95 b*7). hla class i histocompatibility antigen, b-14 alpha chain precursor (mhc class i antigen SW:1B14_HUMAN + - P30462 O02862 P30463 b*14). P30479 O19595 Q29848 hla class i histocompatibility antigen, b-41 alpha chain precursor (mhc class i antigen SW:1B41_HUMAN + - Q9MY79 Q9MY94 b*41) (bw-41). hla class i histocompatibility antigen, b-42 alpha chain precursor (mhc class i antigen SW:1B42_HUMAN + - P30480 P79555 b*42). P30488 O19615 O19624 O19641 O19783 O46702 hla class i histocompatibility antigen, b-50 alpha chain precursor (mhc class i antigen SW:1B50_HUMAN + - O78172 Q9TQG1 b*50) (bw-50) (b-21). hla class i histocompatibility antigen, b-54 alpha chain precursor (mhc class i antigen SW:1B54_HUMAN + - P30492 Q9TPQ9 b*54) (bw-54) (bw-22). P30495 O19758 P30496 hla class i histocompatibility antigen, b-56 alpha chain precursor (mhc class i antigen SW:1B56_HUMAN - + P79490 Q9GIM3 Q9GJ17 b*56) (bw-56) (bw-22). -

Tropomodulin 1 Regulation of Actin Is Required for the Formation of Large Paddle Protrusions Between Mature Lens Fiber Cells
Lens Tropomodulin 1 Regulation of Actin Is Required for the Formation of Large Paddle Protrusions Between Mature Lens Fiber Cells Catherine Cheng,1 Roberta B. Nowak,1 Sondip K. Biswas,2 Woo-Kuen Lo,2 Paul G. FitzGerald,3 and Velia M. Fowler1 1Department of Cell and Molecular Biology, The Scripps Research Institute, La Jolla, California, United States 2Department of Neurobiology, Morehouse School of Medicine, Atlanta, Georgia, United States 3Department of Cell Biology and Human Anatomy, University of California, Davis, California, United States Correspondence: Velia M. Fowler, PURPOSE. To elucidate the proteins required for specialized small interlocking protrusions and Department of Cell and Molecular large paddle domains at lens fiber cell tricellular junctions (vertices), we developed a novel Biology, MB114, The Scripps Re- method to immunostain single lens fibers and studied changes in cell morphology due to loss search Institute, 10550 N. Torrey of tropomodulin 1 (Tmod1), an F-actin pointed end–capping protein. Pines Road, La Jolla, CA 92037, USA; [email protected]. METHODS. We investigated F-actin and F-actin–binding protein localization in interdigitations of þ/þ À/À Submitted: May 17, 2016 Tmod1 and Tmod1 single mature lens fibers. Accepted: June 25, 2016 RESULTS. F-actin–rich small protrusions and large paddles were present along cell vertices of Citation: Cheng C, Nowak RB, Biswas Tmod1þ/þ mature fibers. In contrast, Tmod1À/À mature fiber cells lack normal paddle domains, SK, Lo W-K, FitzGerald PG, Fowler while small protrusions were unaffected. In Tmod1þ/þ mature fibers, Tmod1, b2-spectrin, and VM. Tropomodulin 1 regulation of a-actinin are localized in large puncta in valleys between paddles; but in Tmod1À/À mature actin is required for the formation of fibers, b2-spectrin was dispersed while a-actinin was redistributed at the base of small large paddle protrusions between protrusions and rudimentary paddles. -

Tropomodulin Isoform-Specific Regulation of Dendrite Development and Synapse Formation
The Journal of Neuroscience, November 28, 2018 • 38(48):10271–10285 • 10271 Cellular/Molecular Tropomodulin Isoform-Specific Regulation of Dendrite Development and Synapse Formation Omotola F. Omotade,1,3 XYanfang Rui,1,3 XWenliang Lei,1,3 Kuai Yu,1 H. Criss Hartzell,1 XVelia M. Fowler,4 and X James Q. Zheng1,2,3 Departments of 1Cell Biology, 2Neurology, 3Center for Neurodegenerative Diseases, Emory University School of Medicine, Atlanta, Georgia 30322, and 4Department of Molecular Medicine, Scripps Research Institute, La Jolla, California 92037 Neurons of the CNS elaborate highly branched dendritic arbors that host numerous dendritic spines, which serve as the postsynaptic platform for most excitatory synapses. The actin cytoskeleton plays an important role in dendrite development and spine formation, but the underlying mechanisms remain incompletely understood. Tropomodulins (Tmods) are a family of actin-binding proteins that cap the slow-growing (pointed) end of actin filaments, thereby regulating the stability, length, and architecture of complex actin networks in diverse cell types. Three members of the Tmod family, Tmod1, Tmod2, and Tmod3 are expressed in the vertebrate CNS, but their function in neuronal development is largely unknown. In this study, we present evidence that Tmod1 and Tmod2 exhibit distinct roles in regulat- ing spine development and dendritic arborization, respectively. Using rat hippocampal tissues from both sexes, we find that Tmod1 and Tmod2 are expressed with distinct developmental profiles: Tmod2 is expressed early during hippocampal development, whereas Tmod1 expression coincides with synaptogenesis. We then show that knockdown of Tmod2, but not Tmod1, severely impairs dendritic branch- ing. Both Tmod1 and Tmod2 are localized to a distinct subspine region where they regulate local F-actin stability. -

Proteomic and Functional Analyses of the Periodic Membrane Skeleton in Neurons
bioRxiv preprint doi: https://doi.org/10.1101/2020.12.23.424206; this version posted December 23, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. Title: Proteomic and functional analyses of the periodic membrane skeleton in neurons Authors: Ruobo Zhou1, 5, Boran Han1, 5, Roberta Nowak2, Yunzhe Lu4, Evan Heller1, Chenglong Xia1, Athar H. Chishti4, Velia M. Fowler2,3, Xiaowei Zhuang1,* Affiliations: 1Howard Hughes Medical Institute, Department of Chemistry and Chemical Biology, Department of Physics, Harvard University, Cambridge, MA 02138, USA. 2 Department of Molecular Medicine, The Scripps Research Institute, La Jolla, CA 92307, USA. 3 Department of Biological Sciences, The University of Delaware, Newark, DE 19716, USA 4 Department of Developmental, Molecular, and Chemical Biology, Tufts University School of Medicine, Boston, MA 02111, USA. 5 These authors contributed equally * To whom correspondence may be addressed. Email: [email protected] Abstract Actin, spectrin, and associated molecules form a membrane-associated periodic skeleton (MPS) in neurons. The molecular composition and functions of the MPS remain incompletely understood. Here, using co- immunoprecipitation and mass spectrometry, we identified hundreds of candidate MPS-interacting proteins that span diverse functional categories. We validated representative proteins in several of these categories, including previously unknown MPS structural components, as well as motor proteins, cell adhesion molecules, ion channels, and signaling proteins, demonstrating periodic distributions of ~20 proteins in neurons using super-resolution imaging. -

Multifunctional Roles of Tropomodulin-3 in Regulating Actin Dynamics
Multifunctional roles of Tropomodulin-3 in regulating actin dynamics Tropomodulins (Tmods) are proteins that cap the slow growing (pointed) ends of actin filaments (F-actin). The basis for our current understanding of Tmod function comes from studies in cells with relatively stable and highly organized F-actin networks, leading to the view that Tmod capping functions principally to preserve F-actin stability. However, not only is Tmod capping dynamic, but it also can play major roles in regulating diverse cellular processes involving F-actin remodeling. Here, we highlight the multifunctional roles of Tmod with a focus on Tmod3. Like other Tmods, Tmod3 binds tropomyosin (Tpm) and actin, capping pure F-actin at submicromolar and Tpm-coated F-actin at nanomolar concentrations. Unlike other Tmods, Tmod3 can also bind actin monomers and its ability to bind actin is inhibited by phosphorylation of Tmod3 by Akt2. Tmod3 is ubiquitously expressed and present in a diverse array of cytoskeletal structures, including contractile structures such as sarcomere-like units of actomyosin stress fibers and in the F-actin network encompassing adherens junctions. Tmod3 participates in F-actin network remodeling in lamellipodia during cell migration, and in the assembly of specialized F-actin networks during exocytosis. Furthermore, Tmod3 is required for development, regulating F-actin mesh formation during meiosis I of mouse oocytes, erythroblast enucleation in definitive erythropoiesis, and megakaryocyte morphogenesis in the mouse fetal liver. Thus, Tmod3 plays vital roles in dynamic and stable F-actin networks in cell physiology and development, with further research required to delineate the mechanistic details of Tmod3 regulation in the aforementioned processes, or in other yet to be discovered processes.