DOCSLIB.ORG

Supercritical Fluid Chromatography

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Supercritical Fluid Chromatography SUPERCRITICAL FLUID CHROMATOGRAPHY SUPERCRITICAL FLUID CHROMATOGRAPHY Primer Primer SUPERCRITICAL FLUID CHROMATOGRAPHY Primer Terry A. Berger This information is subject to change without notice. © Agilent Technologies, Inc., 2015 Printed in the USA, July 1, 2015 5991-5509EN CONTENTS Contents III Foreword VI About the Author XI Introduction XIII Symbols XIV Abbreviations XIV 1 Introduction to Supercritical Fluid Chromatography 1 1.1 What is SFC? 1 1.2 Why deploy SFC? 2 1.3 What can SFC separate? 12 1.4 What’s in a name? 16 2 The Mobile Phase 19 2.1 Why use CO2? 19 2.2 Using 100 % CO2 21 2.3 Modifiers or cosolvents 23 2.4 Additives 31 2.5 Extending solute polarity with added water 34 3 The Stationary Phase 35 3.1 Materials 35 3.2 Achiral bonded phases 35 3.3 Stationary phase comparisons 40 3.4 Relationship between particle diameter and column dimensions 41 3.5 Recommended column dimensions 45 3.6 Columns for chiral separations 48 III 4 Effect of Mobile Phase Variables on Retention and Selectivity 49 4.1 Modifier concentration 49 4.2 Temperature 50 4.3 Pressure 53 4.4 Flow 55 4.5 Generalizations on effects of control variables on retention and selectivity 57 5 Method Development 58 5.1 Matching solute and phase polarity 58 5.2 Polarity windows 60 5.3 Getting started 60 5.4 Polar solutes 61 5.5 Low polarity solutes 64 5.6 Multivariate methods 65 6 Achiral Separations 66 6.1 Case Study 1 – A typical low-polarity sample 66 6.2 Case study 2 – A moderately polar sample 71 6.3 Case study 3 – Sulfonamides 83 6.4 Other observations 89 7 Chiral Separations 90 7.1 Background 90 7.2 Enantiomeric excess determinations 91 7.3 Normal phase for chiral separations 91 7.4 Effect of control variables on chiral separations 93 7.5 Developing a chiral method 98 IV 8 Quantification in SFC 103 8.1 Stages of Validation 103 8.2 Method development for quantification of sorbate, benzoate, and caffeine in beverages and foods 105 8.3 Calibration 108 8.4 Summary of the quantification of benzoate, sorbate and caffeine 116 8.5 Chiral separations 116 9 Instrumental Considerations 121 9.1 Pumping 121 9.2 UV detector optimization 124 9.3 The doubling gradient 137 9.4 Autosampler considerations 138 9.5 Miscellaneous 146 9.6 Ultrahigh performance with SFC 148 9.7 Hybrid systems switching between SFC and HPLC 150 9.8 Interfacing to mass spectrometers 154 9.9 Other Detectors 156 References 159 V FOREWORD The author, Terry Berger has a unique, convoluted history with what we now call supercritical fluid chromatography (SFC), and is uniquely qualified to write this primer. Many of the early interactions were incidental and unfocused, but later meaningful. He brings nearly 40 years of relationships with people associated with SFC, along with over 35 years of direct experience. SFC had first been proposed nearly 60 years ago, in 1958, by Jim Lovelock, who later became a personal friend of the author through the 1980s and 1990s with numerous discussions about SFC. Ernst Klesper demonstrated SFC experimentally in 1962 when he separated metal porphorins with dense clorofluorocarbons as mobile phase. The author later interacted with Professor Klesper on numerous occasions, through the late 1970s to mid-1980s in both the USA and Germany, and again had extensive discussions about SFC. Through the 1960s and 1970s, the technique largely languished with, at most, a dozen groups worldwide making a total of a few sporadic scientific contributions per year. Applications tended to be extensions of gas chromatography (GC) to higher molecular weight, higher boiling, relatively nonpolar solutes. In the early 1970s, the author was a graduate student at Purdue University in Indiana. The adjacent laboratory was that of L.B. “Buck” Rodgers, a highly respected chromatographer at the time. After attending a scientific symposium in 1971, he came back determined to explore this new form of chromatography. Controlling the pressure of the mobile phase was the primary control variable, and pressure programming from low to high pressures was then the norm. All equipment in this period was homemade, with poor instrumental control. The physical and chemical characteristics of the mobile phases were primitively understood, at best. Rodgers rescued ultrahigh pressure hydrogenation pumps from storage, built an oven roughly 4-feet long that looked like a small coffin using 2-inch thick household foam insulation. Columns were 30 inches long or longer, and packed with irregular particles with a wide particle-size distribution. The author watched the progression of these developments and recalls that, at the time, being skeptical that this odd form of chromatography was useful. Rodgers results suggested there was a serious problem with density gradients along the length of VI the column. This, and later work by Milos Novotney, seemed to indicate that the technique was unlikely to produce results as good as the current high-performance liquid chromatography (HPLC). This tended to suppress further work on packed-column SFC. The author was trained in HPLC at Imperial College in London where he developed an amperometric electrochemical detector for HPLC, in the early 1970s. After subsequently teaching for a year in Brazil, he worked on a number of projects for instrumentation for spacecraft in Cleveland, Ohio. The author was then hired by Hewlett-Packard in 1979, and joined the research group at the Avondale Division. Dennis Gere, Henk Lauer, Doug McManigill, and Harry Weaver, all scientists or engineers at Hewlett-Packard Labs or the Avondale Division, presented a series of talks on dense gas chromatography at that year’s Pittsburg Conference (where the author was actually hired). Some of these talks were later published in such journals as Analytical Chemistry, and Science, as well as related application notes. These works resulted in a customer demand that led to the creation of a commercial kit that converted a Hewlett-Packard model HP 1084 HPLC instrument into an SFC system. Thus, commercial SFC was born. This version of SFC used a mechanical backpressure regulator, a binary pump and composition programming, much like HPLC. Flow, composition, column temperature, and column outlet pressure were all independently controlled. Unlike previously home-built instruments, there was no pressure programming. Columns were more modern with much of the work done on spherical silica as small as 3 µm. The author’s group produced the design for this kit. About the same time that a capillary version of SFC, using pressure programming of pure CO2, was introduced, Hewlett-Packard made the HP 1084 instrument obsolete, replacing it with the SFC-incompatible HP 1090 HPLC instrument. Milos Novotny and Milton Lee were the drivers behind the capillary SFC development. This author’s research group at Hewlett-Packard had just invented fused-silica capillary columns, capable of withstanding the high pressures (400 to 600 bar) necessary for capillary SFC. Milton Lee was an academic leader in the new field of bonding the stationary phase to capillary columns. VII Packed-column SFC largely disappeared, due to lack of commercially available instrumentation, and capillary SFC was seen as the wave of the future. At this time, the physical chemistry of the fluids and their interaction with the stationary phase were largely unknown. Many controversies erupted pitting the few remaining packed column users against the capillary proponents. The author became the senior research scientist working with SFC at Hewlett-Packard in 1985, and was assigned to unravel these controversies. In the process, he visited every European user (about 16) for extensive discussions about the controversies and potential. At the time, it was widely believed that density was the primary control variable, and that changing the mobile phase density had the biggest effect on retention. It was thought that dense CO2 was as polar as isopropanol, due to an unfortunate misunderstanding by Giddings1. If it were true, adding an alcohol modifier could change density significantly, but only insignificantly change solvent strength. This misinterpretation was not challenged for decades. At the time, there were no direct density measurements of methanol/CO2 (or any other) mixtures used in SFC. Equations of state for binary mixtures were inaccurate. The author subsequently borrowed a densitometer from the University of Delaware and made some of the first density measurements of methanol/CO2 in the literature. He then measured the effect of methanol concentration on retention at constant density, showing that the modifier was indeed responsible for dramatically increasing the elutropic strength of the mobile phase. Not long afterwards, solvatochromic dyes were shown to offer a simple way to measure the strength and polarity of the solvation sphere surrounding the dye molecules in HPLC2. The author then applied the same principle to SFC45. The results indicated that the solvent strength of binary fluids was highly nonlinear, with the first small additions having an inordinate effect. CO2 was shown to be similar to pentane in polarity and solvent strength. With density and solvatochromaic dye measurements, the Giddings’ elutropic series1 was conclusively revised, although it still has followers. The result is that changing modifier concentration was shown to have a much larger impact on retention than pressure, temperature, and density, at least for modified fluids. It was widely demonstrated during the late 1980s that many polar solutes such as organic acids and bases eluted with poor peak shapes or did not elute at all when using binary fluids consisting of CO2 modified with an alcohol such as methanol or ethanol. It was generally thought that this indicated that the stationary phase was too active or contained VIII active sites that interacted too strongly with these polar solutes.
Load more

Recommended publications
  • Lecture Notes: BCS Theory of Superconductivity
    Lecture Notes: BCS theory of superconductivity Prof. Rafael M. Fernandes Here we will discuss a new ground state of the interacting electron gas: the superconducting state. In this macroscopic quantum state, the electrons form coherent bound states called Cooper pairs, which dramatically change the macroscopic properties of the system, giving rise to perfect conductivity and perfect diamagnetism. We will mostly focus on conventional superconductors, where the Cooper pairs originate from a small attractive electron-electron interaction mediated by phonons. However, in the so- called unconventional superconductors - a topic of intense research in current solid state physics - the pairing can originate even from purely repulsive interactions. 1 Phenomenology Superconductivity was discovered by Kamerlingh-Onnes in 1911, when he was studying the transport properties of Hg (mercury) at low temperatures. He found that below the liquifying temperature of helium, at around 4:2 K, the resistivity of Hg would suddenly drop to zero. Although at the time there was not a well established model for the low-temperature behavior of transport in metals, the result was quite surprising, as the expectations were that the resistivity would either go to zero or diverge at T = 0, but not vanish at a finite temperature. In a metal the resistivity at low temperatures has a constant contribution from impurity scattering, a T 2 contribution from electron-electron scattering, and a T 5 contribution from phonon scattering. Thus, the vanishing of the resistivity at low temperatures is a clear indication of a new ground state. Another key property of the superconductor was discovered in 1933 by Meissner.
    [Show full text]
  • Supercritical Fluid Extraction of Positron-Emitting Radioisotopes from Solid Target Matrices
    XA0101188 11. United States of America Supercritical Fluid Extraction of Positron-Emitting Radioisotopes From Solid Target Matrices D. Schlyer, Brookhaven National Laboratory, Chemistry Department, Upton, Bldg. 901, New York 11973-5000, USA Project Description Supercritical fluids are attractive as media for both chemical reactions, as well as process extraction since their physical properties can be manipulated by small changes in pressure and temperature near the critical point of the fluid. What is a supercritical fluid? Above a certain temperature, a vapor can no longer be liquefied regardless of pressure critical temperature - Tc supercritical fluid r«gi on solid a u & temperature Fig. 1. Phase diagram depicting regions of solid, liquid, gas and supercritical fluid behavior. The critical point is defined by a critical pressure (Pc) and critical temperature (Tc) for a particular substance. Such changes can result in drastic effects on density-dependent properties such as solubility, refractive index, dielectric constant, viscosity and diffusivity of the fluid[l,2,3]. This suggests that pressure tuning of a pure supercritical fluid may be a useful means to manipulate chemical reactions on the basis of a thermodynamic solvent effect. It also means that the solvation properties of the fluid can be precisely controlled to enable selective component extraction from a matrix. In recent years there has been a growing interest in applying supercritical fluid extraction to the selective removal of trace metals from solid samples [4-10]. Much of the work has been done on simple systems comprised of inert matrices such as silica or cellulose. Recently, this process as been expanded to environmental samples as well [11,12].
    [Show full text]
  • General Introduction to the Chemistry of Dyes
    GENERAL INTRODUCTION TO THE CHEMISTRY OF DYES 1. Principles of Colour Chemistry 1.1 Basis for colour Unlike most organic compounds, dyes possess colour because they 1) absorb light in the visible spectrum (400–700 nm), 2) have at least one chromophore (colour-bearing group), 3) have a conjugated system, i.e. a structure with alternating double and single bonds, and 4) exhibit resonance of electrons, which is a stabilizing force in organic compounds (Abrahart, 1977). When any one of these features is lacking from the molecular structure the colour is lost. In addition to chromophores, most dyes also contain groups known as auxochromes (colour helpers), examples of which are carboxylic acid, sulfonic acid, amino, and hydroxyl groups. While these are not responsible for colour, their presence can shift the colour of a colourant and they are most often used to influence dye solubility. Figure 1 shows the relationships between wavelength of visible and colour absorbed/observed. Other factors contributing to colour are illustrated in Figures 2–4. Fig. 1. Wavelength of light absorption versus colour in organic dyes Wavelength Absorbed (nm) Colour Absorbed Colour Observed 400–435 Violet Yellow-Green 435–480 Blue Yellow 480–490 Green-Blue Orange 490–500 Blue-Green Red 500–560 Green Purple 560–580 Yellow-Green Violet 580–595 Yellow Blue 595–605 Orange Green-Blue 605–700 Red Blue-Green –55– 56 IARC MONOGRAPHS VOLUME 99 Fig. 2. Examples of chromophoric groups present in organic dyes O O N N N N O N N O H N Anthraquinone H N Nitro Azo N N Ar C N N C Ar Methine Phthalocyanine Triarylmethane Fig.
    [Show full text]
  • Equation of State and Phase Transitions in the Nuclear
    National Academy of Sciences of Ukraine Bogolyubov Institute for Theoretical Physics Has the rights of a manuscript Bugaev Kyrill Alekseevich UDC: 532.51; 533.77; 539.125/126; 544.586.6 Equation of State and Phase Transitions in the Nuclear and Hadronic Systems Speciality 01.04.02 - theoretical physics DISSERTATION to receive a scientific degree of the Doctor of Science in physics and mathematics arXiv:1012.3400v1 [nucl-th] 15 Dec 2010 Kiev - 2009 2 Abstract An investigation of strongly interacting matter equation of state remains one of the major tasks of modern high energy nuclear physics for almost a quarter of century. The present work is my doctor of science thesis which contains my contribution (42 works) to this field made between 1993 and 2008. Inhere I mainly discuss the common physical and mathematical features of several exactly solvable statistical models which describe the nuclear liquid-gas phase transition and the deconfinement phase transition. Luckily, in some cases it was possible to rigorously extend the solutions found in thermodynamic limit to finite volumes and to formulate the finite volume analogs of phases directly from the grand canonical partition. It turns out that finite volume (surface) of a system generates also the temporal constraints, i.e. the finite formation/decay time of possible states in this finite system. Among other results I would like to mention the calculation of upper and lower bounds for the surface entropy of physical clusters within the Hills and Dales model; evaluation of the second virial coefficient which accounts for the Lorentz contraction of the hard core repulsing potential between hadrons; inclusion of large width of heavy quark-gluon bags into statistical description.
    [Show full text]
  • Identification and Distribution of Dietary Precursors of The
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Vision Research 39 (1999) 219–229 Identification and distribution of dietary precursors of the Drosophila visual pigment chromophore: analysis of carotenoids in wild type and ninaD mutants by HPLC David R. Giovannucci *, Robert S. Stephenson Department of Biological Sciences, Wayne State Uni6ersity, Detroit, MI 48202, USA Received 3 July 1997; received in revised form 10 November 1997 Abstract A dietary source of retinoid or carotenoid has been shown to be necessary for the biosynthesis of functional visual pigment in flies. In the present study, the larvae or adults of Drosophila melanogaster were administered specific carotenoid-containing diets and high performance liquid chromatography was used to identify and quantify the carotenoids in extracts of wild type and ninaD visual mutant flies. When b-carotene was fed to larvae, wild type flies were shown to hydroxylate this molecule and to accumulate zeaxanthin and a small amount of b-cryptoxanthin. Zeaxanthin content was found to increase throughout development and was a major carotenoid peak detected in the adult fly. Carotenoids were twice as effective at mediating zeaxanthin accumulation when provided to larvae versus adults. In the ninaD mutant, zeaxanthin content was shown to be specifically and significantly altered compared to wild type, and was ineffective at mediating visual pigment synthesis when provided to both larval and adult mutant flies. It is proposed that zeaxanthin is the larval storage form for subsequent visual pigment chromophore biosynthesis during pupation, that zeaxanthin or b-crytoxanthin is the immediate precursor for light-independent chromophore synthesis in the adult, and that the ninaD mutant is defective in this pathway.
    [Show full text]
  • Ba3(P1−Xmnxo4)2 : Blue/Green Inorganic Materials Based on Tetrahedral Mn(V)
    Bull. Mater. Sci., Vol. 34, No. 6, October 2011, pp. 1257–1262. c Indian Academy of Sciences. Ba3(P1−xMnxO4)2 : Blue/green inorganic materials based on tetrahedral Mn(V) SOURAV LAHA, ROHIT SHARMA, S V BHAT†, MLPREDDY‡, J GOPALAKRISHNAN∗ and S NATARAJAN Solid State and Structural Chemistry Unit, †Department of Physics, Indian Institute of Science, Bangalore 560 012, India ‡Chemical Science and Technology Division, National Institute for Interdisciplinary Science and Technology (NIIST), Thiruvananthapuram 695 019, India MS received 11 May 2011 ) 3− 2 Abstract. We describe a blue/green inorganic material, Ba3(P1−xMnxO4 2 (I) based on tetrahedral MnO4 :3d chromophore. The solid solutions (I) which are sky-blue and turquoise-blue for x ≤ 0·25 and dark green for x ≥ 0·50, 3− are readily synthesized in air from commonly available starting materials, stabilizing the MnO4 chromophore in an isostructural phosphate host. We suggest that the covalency/ionicity of P–O/Mn–O bonds in the solid solutions tunes the crystal field strength around Mn(V) such that a blue colour results for materials with small values of x. The material could serve as a nontoxic blue/green inorganic pigment. Keywords. Blue/green inorganic material; barium phosphate/manganate(V); tetrahedral manganate(V); blue/green chromophore; ligand field tuning of colour. 1. Introduction field transitions within an unusual five coordinated trigo- nal bipyramidal Mn(III). A turquoise-blue solid based on Inorganic solids displaying bright colours are important Li1·33Ti1·66O4 spinel oxide wherein the colour arises from as pigment materials which find a wide range of appli- an intervalence charge-transfer between Ti3+ and Ti4+ has cations in paints, inks, plastics, rubbers, ceramics, ena- also been described recently (Fernández-Osorio et al 2011).
    [Show full text]
  • Color Vision Light
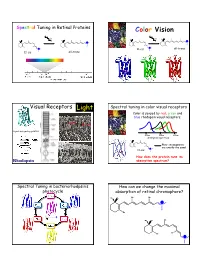
    Spectral Tuning in Retinal Proteins Color Vision hν hν N N H H H H N all-trans N 11-cis 11-cis all-trans Visual Receptors Light Spectral tuning in color visual receptors Color is sensed by red, green and blue rhodopsin visual receptors. Rod Cone G-protein signaling pathway 400nm 500nm 600nm absorption spectrum Their chromophores H are exactly the same! 11-cis N How does the protein tune its Rhodopsin absorption spectrum? Spectral Tuning in bacteriorhodpsin’s How can we change the maximal photocycle absorption of retinal chromophore? Me Me Me Me N H Me Me Me Me N H Me Me Me Me Me Me Me H N 1 Excitation energy determines the Electronic Absorption maximal absorption Me Me Me Me π π* N - H S1 Me Absorption of light in the UV-VIS region of the S0 spectrum is due to Response excitation of electrons to higher energy levels. Me Me Me 13 7911 15 N H Me Me π-π* excitation in polyenes π-π* excitation in polyenes π∗ π∗ π∗ π∗ ∆E π∗ E photon E π π π π π Ground state (S0) Excited state (S1) ∆E (excitation energy, band gap) = hν = hc/λ blue-shift red-shift π-π* excitation in polyenes Tuning the length of the conjugated backbone β-carotene O O Vitamin A2 (retinal II) Vitamin A1 (retinal I) Longer wavelength Short wavelength 2 Retinal I Retinal II OPSIN SHIFT: how protein tunes the absorption maximum of its chromophore. Maximal absorption of protonated retinal Schiff base in: Water/methanol solution: 440 nm bR: 568 nm rod Rh: 500 nm red receptor: 560 nm green receptor: 530 nm blue receptor: 426 nm Salmon: different retinals in different stages of life Electrostatics and opsin shift Electrostatics and opsin shift S S positive charge 2 positive charge 2 S2 S2 Me Me Me Me Me Me S1 S1 S1 S1 + + + + N N H H Me O S0 Me O S0 Me O Me O C C Asp (Glu) Asp (Glu) S0 S0 no protein in protein no protein in protein counterion counterion • The counterion stabilizes the positive charge of the chromophore.
    [Show full text]
  • Lecture 5 Non-Aqueous Phase Liquid (NAPL) Fate and Transport
    Lecture 5 Non-Aqueous Phase Liquid (NAPL) Fate and Transport Factors affecting NAPL movement Fluid properties: Porous medium: 9 Density Permeability 9 Interfacial tension Pore size 9 Residual saturation Structure Partitioning properties Solubility Ground water: Volatility and vapor density Water content 9 Velocity Partitioning processes NAPL can partition between four phases: NAPL Gas Solid (vapor) Aqueous solution Water to gas partitioning (volatilization) Aqueous ↔ gaseous Henry’s Law (for dilute solutions) 3 Dimensionless (CG, CW in moles/m ) C G = H′ CW Dimensional (P = partial pressure in atm) P = H CW Henry’s Law Constant H has dimensions: atm m3 / mol H’ is dimensionless H’ = H/RT R = gas constant = 8.20575 x 10-5 atm m3/mol °K T = temperature in °K NAPL to gas partitioning (volatilization) NAPL ↔ gaseous Raoult’s Law: CG = Xt (P°/RT) Xt = mole fraction of compound in NAPL [-] P° = pure compound vapor pressure [atm] R = universal gas constant [m3-atm/mole/°K] T = temperature [°K] Volatility Vapor pressure P° is measure of volatility P° > 1.3 x 10-3 atm → compound is “volatile” 1.3 x 10-3 > P° > 1.3 x 10-13 atm → compound is “semi-volatile” Example: equilibrium with benzene P° = 76 mm Hg at 20°C = 0.1 atm R = 8.205 x 10-5 m3-atm/mol/°K T = 20°C (assumed) = 293°K Assume 100% benzene, mole fraction Xt = 1 3 CG = Xt P°/(RT) = 4.16 mol/m Molecular weight of benzene, C6H6 = 78 g/mol 3 3 CG = 4.16 mol/m × 78 g/mol = 324 g/m = 0.32 g/L 6 CG = 0.32 g/L x 24 L/mol / (78 g/mol) x 10 = 99,000 ppmv One mole of ideal gas = 22.4 L at STP (1 atm, 0 C), Corrected to 20 C: 293/273*22.4 = 24.0 L/mol Gas concentration in equilibrium with pure benzene NAPL Example: equilibrium with gasoline Gasoline is complex mixture – mole fraction is difficult to determine and varies Benzene = 1 to several percent (Cline et al., 1991) Based on analysis reported by Johnson et al.
    [Show full text]
  • Introduction to Unconventional Superconductivity Manfred Sigrist
    Introduction to Unconventional Superconductivity Manfred Sigrist Theoretische Physik, ETH-Hönggerberg, 8093 Zürich, Switzerland Abstract. This lecture gives a basic introduction into some aspects of the unconventionalsupercon- ductivity. First we analyze the conditions to realized unconventional superconductivity in strongly correlated electron systems. Then an introduction of the generalized BCS theory is given and sev- eral key properties of unconventional pairing states are discussed. The phenomenological treatment based on the Ginzburg-Landau formulations provides a view on unconventional superconductivity based on the conceptof symmetry breaking.Finally some aspects of two examples will be discussed: high-temperature superconductivity and spin-triplet superconductivity in Sr2RuO4. Keywords: Unconventional superconductivity, high-temperature superconductivity, Sr2RuO4 INTRODUCTION Superconductivity remains to be one of the most fascinating and intriguing phases of matter even nearly hundred years after its first observation. Owing to the breakthrough in 1957 by Bardeen, Cooper and Schrieffer we understand superconductivity as a conden- sate of electron pairs, so-called Cooper pairs, which form due to an attractive interaction among electrons. In the superconducting materials known until the mid-seventies this interaction is mediated by electron-phonon coupling which gises rise to Cooper pairs in the most symmetric form, i.e. vanishing relative orbital angular momentum and spin sin- glet configuration (nowadays called s-wave pairing). After the introduction of the BCS concept, also studies of alternative pairing forms started. Early on Anderson and Morel [1] as well as Balian and Werthamer [2] investigated superconducting phases which later would be identified as the A- and the B-phase of superfluid 3He [3]. In contrast to the s-wave superconductors the A- and B-phase are characterized by Cooper pairs with an- gular momentum 1 and spin-triplet configuration.
    [Show full text]
  • Phase Diagrams a Phase Diagram Is Used to Show the Relationship Between Temperature, Pressure and State of Matter
    Phase Diagrams A phase diagram is used to show the relationship between temperature, pressure and state of matter. Before moving ahead, let us review some vocabulary and particle diagrams. States of Matter Solid: rigid, has definite volume and definite shape Liquid: flows, has definite volume, but takes the shape of the container Gas: flows, no definite volume or shape, shape and volume are determined by container Plasma: atoms are separated into nuclei (neutrons and protons) and electrons, no definite volume or shape Changes of States of Matter Freezing start as a liquid, end as a solid, slowing particle motion, forming more intermolecular bonds Melting start as a solid, end as a liquid, increasing particle motion, break some intermolecular bonds Condensation start as a gas, end as a liquid, decreasing particle motion, form intermolecular bonds Evaporation/Boiling/Vaporization start as a liquid, end as a gas, increasing particle motion, break intermolecular bonds Sublimation Starts as a solid, ends as a gas, increases particle speed, breaks intermolecular bonds Deposition Starts as a gas, ends as a solid, decreases particle speed, forms intermolecular bonds http://phet.colorado.edu/en/simulation/states- of-matter The flat sections on the graph are the points where a phase change is occurring. Both states of matter are present at the same time. In the flat sections, heat is being removed by the formation of intermolecular bonds. The flat points are phase changes. The heat added to the system are being used to break intermolecular bonds. PHASE DIAGRAMS Phase diagrams are used to show when a specific substance will change its state of matter (alignment of particles and distance between particles).
    [Show full text]
  • Indigo Chromophores and Pigments Structure and Dynamics
    Dyes and Pigments 172 (2020) 107761 Contents lists available at ScienceDirect Dyes and Pigments journal homepage: www.elsevier.com/locate/dyepig Indigo chromophores and pigments: Structure and dynamics T ∗ V.V. Volkova, R. Chellib, R. Righinic, C.C. Perrya, a Interdisciplinary Biomedical Research Centre, School of Science and Technology, Nottingham Trent University, Clifton Lane, Nottingham, NG11 8NS, United Kingdom b Dipartimento di Chimica, Università degli Studi di Firenze, Via della Lastruccia 3, Sesto Fiorentino, 50019, Italy c European Laboratory for Non-Linear Spectroscopy (LENS), Università degli Studi di Firenze, Via Nello Carrara 1, Sesto Fiorentino, 50019, Italy ARTICLE INFO ABSTRACT Keywords: In this study, we explore the molecular mechanisms of the stability of indigo chromophores and pigments. Indigo Assisted with density functional theory, we compare visible, infrared and Raman spectral properties of model Raman molecules, chromophores and pigments derived from living organisms. Using indigo carmine as a representative Infrared model system, we characterize the structure and dynamics of the chromophore in the first electronic excited Density functional theory state using femtosecond visible pump-infrared probe spectroscopy. Results of experiments and theoretical stu- Excited state dies indicate that, while the trans geometry is strongly dominant in the electronic ground state, upon photo- excitation, in the Franck-Condon region, some molecules may experience isomerization and proton transfer dynamics. If this happens, however, the normal modes of the trans geometry of the electronic excited state are reconfirmed within several hundred femtoseconds. Supported by quantum theory, first, we ascribe stabilization of the trans geometry in the Franck-Condon region to the reactive character of the potential energy surface for the indigo chromophore when under the cis geometry in the electronic excited state.
    [Show full text]
  • States of Matter
    States of Matter A Museum of Science Traveling Program Description States of Matter is a 60- minute presentation about the characteristics of solids, liquids, gases, and the temperature- dependent transitions between them. It is designed to build on NGSS-based curricula. NGSS: Next Generation Science Standards Needs We bring all materials and equipment, including a video projector and screen. Access to 110- volt electricity is required. Space Requirements The program can be presented in assembly- suitable spaces like gyms, multipurpose rooms, cafeterias, and auditoriums. Goals: Changing State A major goal is to show that all substances will go through phase changes and that every substance has its own temperatures at which it changes state. Goals: Boiling Liquid nitrogen boils when exposed to room temperature. When used with every day objects, it can lead to unexpected results! Goals: Condensing Placing balloons in liquid nitrogen causes the gas inside to condense, shrinking the balloons before the eyes of the audience! Latex-free balloons are available for schools with allergic students. Goals: Freezing Nitrogen can also be used to flash-freeze a variety of liquids. Students are encouraged to predict the results, and may end up surprised! Goals: Behavior Changes When solids encounter liquid nitrogen, they can no longer change state, but their properties may have drastic—sometimes even shattering— changes. Finale Likewise, the properties of gas can change at extreme temperatures. At the end of the program, a blast of steam is superheated… Finale …incinerating a piece of paper! Additional Content In addition to these core goals, other concepts are taught with a variety of additional demonstrations.
    [Show full text]