DOCSLIB.ORG

LECTURE 12 FIRST LAW of THERMODYNAMICS Lecture Instructor: Kazumi Tolich Lecture 12

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
LECTURE 12 FIRST LAW of THERMODYNAMICS Lecture Instructor: Kazumi Tolich Lecture 12 1 LECTURE 12 FIRST LAW OF THERMODYNAMICS Lecture instructor: Kazumi Tolich Lecture 12 2 ¨ Reading chapter 15-1 to 15-2 ¤ First law of thermodynamics ¤ Work n Work and the PV diagram for a gas ¤ Thermal processes n Constant pressure n Constant volume n Isothermal n Adiabatic First law of thermodynamics 3 ¨ The first law of thermodynamics is a statement of the conservation of energy. ¨ The change in a system’s internal energy ΔU is related to the heat Q and the work W as follows: ΔU = Q −W Internal energy vs. heat and work 4 ¨ The state of a system is determined by its temperature, pressure, and volume. It is an intrinsic property of a system. ¨ The internal energy of the system depends only on the state of the system, its temperature, so the internal energy is a state function. ¨ The work done and the heat added, however, depend on the details of the process involved, so they are not state functions. ¨ We cannot say that a system “contains” a certain amount of heat or work. Example: 1 5 ¨ One mole of an ideal monoatomic gas is initially at a temperature of Ti = 283 K. a) Find the final temperature of the gas, Tf, if Q = 3280 J of heat is added to it, and it does W = 722 J of work. b) Suppose the amount of the gas is doubled. Does Tf in a) increase, decrease, or stay the same? Thermal process assumptions 6 ¨ All thermal processes are quasi-static. ¤ They are slow enough that the system is always in equilibrium. ¤ The pressure and temperature are uniform throughout the system. ¨ All thermal processes are reversible. ¤ For a process to be reversible, it must be possible to return both the system and its surroundings to exactly the same states in which they were before the process began. Irreversible processes 7 ¨ Examples of irreversible (not reversible) processes: ¤ Friction between a piston and the cylinder generate heat that escapes the cylinder. ¤ A process occurs rapidly to cause turbulence. ¤ A process occurs rapidly without being in equilibrium. ¨ In practice, all real processes are irreversible, but we can approximate many processes with a reversible process. Work and PV plot 8 ¨ The work done by an expanding gas is equal to the area under the curve representing the process in a pressure vs. volume plot (PV plot). ¨ The area under the curve is negative if ΔV is negative. Clicker question: 1 9 Constant pressure process 10 ¨ In a process under a constant pressure P, work done by an expanding gas W as the volume of the gas changes by ΔV is given by W = PΔV Example: 2 11 ¨ An ideal gas is compressed at constant pressure to one- half its original volume. If the pressure of the gas is P = 120 kPa, and 760 J of work is done on it, find the initial volume of the gas. Constant volume process 12 ¨ In a constant-volume process, nothing moves, and no work is done on the surrounding. W = 0 Isothermal process 13 ¨ In an isothermal process, the temperature T is constant. ¨ From the equation of state for an ideal gas, you see that PV = NkT = nRT = constant. ¨ The pressure varies inversely with the volume. ¨ The work done by an expanding gas is given by !V $ !V $ W = NkT ln# f & = nRT ln# f & "Vi % "Vi % Example: 3 14 ¨ Suppose n = 145 moles of a monoatomic ideal gas undergo an isothermal expansion 3 3 from Vi = 1.00 m to Vf = 4.00 m . a) What is the temperature at the beginning and at the end of this process? b) How much work is done by the gas during this expansion? Adiabatic process 15 ¨ An adiabatic process is one in which no heat flows into or out of the system, Q = 0. ¨ The adiabatic PV curve is similar to the isothermal one, but is steeper. ¨ Adiabatic process can be created by the following: ¤ Thermally insulate the system ¤ Have the volume change occur very quickly so that the heat has no time to flow in or out of the system. ¨ Since ΔU = Q − W, the work done by the gas is given by W = −ΔU Example: 4 16 ¨ During an adiabatic process, the temperature of a monoatomic ideal gas drops from Ti = 495 °C to Tf = 215 °C . If the gas does W = 19.2 kJ of work, how many moles of molecules are there is the gas? Demo: 1 17 ¨ Fire syringe ¨ Temperature change with compression ¤ Demonstration of adiabatic process n Rapid compression causing temperature to raise. Summary 18 ¨ Various thermodynamic processes and their characteristics Clicker question: 2 19.
Load more

Recommended publications
  • 3-1 Adiabatic Compression
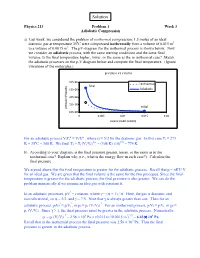
    Solution Physics 213 Problem 1 Week 3 Adiabatic Compression a) Last week, we considered the problem of isothermal compression: 1.5 moles of an ideal diatomic gas at temperature 35oC were compressed isothermally from a volume of 0.015 m3 to a volume of 0.0015 m3. The pV-diagram for the isothermal process is shown below. Now we consider an adiabatic process, with the same starting conditions and the same final volume. Is the final temperature higher, lower, or the same as the in isothermal case? Sketch the adiabatic processes on the p-V diagram below and compute the final temperature. (Ignore vibrations of the molecules.) α α For an adiabatic process ViTi = VfTf , where α = 5/2 for the diatomic gas. In this case Ti = 273 o 1/α 2/5 K + 35 C = 308 K. We find Tf = Ti (Vi/Vf) = (308 K) (10) = 774 K. b) According to your diagram, is the final pressure greater, lesser, or the same as in the isothermal case? Explain why (i.e., what is the energy flow in each case?). Calculate the final pressure. We argued above that the final temperature is greater for the adiabatic process. Recall that p = nRT/ V for an ideal gas. We are given that the final volume is the same for the two processes. Since the final temperature is greater for the adiabatic process, the final pressure is also greater. We can do the problem numerically if we assume an idea gas with constant α. γ In an adiabatic processes, pV = constant, where γ = (α + 1) / α.
    [Show full text]
  • Lecture 2 the First Law of Thermodynamics (Ch.1)
    Lecture 2 The First Law of Thermodynamics (Ch.1) Outline: 1. Internal Energy, Work, Heating 2. Energy Conservation – the First Law 3. Quasi-static processes 4. Enthalpy 5. Heat Capacity Internal Energy The internal energy of a system of particles, U, is the sum of the kinetic energy in the reference frame in which the center of mass is at rest and the potential energy arising from the forces of the particles on each other. system Difference between the total energy and the internal energy? boundary system U = kinetic + potential “environment” B The internal energy is a state function – it depends only on P the values of macroparameters (the state of a system), not on the method of preparation of this state (the “path” in the V macroparameter space is irrelevant). T A In equilibrium [ f (P,V,T)=0 ] : U = U (V, T) U depends on the kinetic energy of particles in a system and an average inter-particle distance (~ V-1/3) – interactions. For an ideal gas (no interactions) : U = U (T) - “pure” kinetic Internal Energy of an Ideal Gas f The internal energy of an ideal gas U = Nk T with f degrees of freedom: 2 B f ⇒ 3 (monatomic), 5 (diatomic), 6 (polyatomic) (here we consider only trans.+rotat. degrees of freedom, and neglect the vibrational ones that can be excited at very high temperatures) How does the internal energy of air in this (not-air-tight) room change with T if the external P = const? f ⎡ PV ⎤ f U =Nin room k= T Bin⎢ N room = ⎥ = PV 2 ⎣ kB T⎦ 2 - does not change at all, an increase of the kinetic energy of individual molecules with T is compensated by a decrease of their number.
    [Show full text]
  • Lecture 4: 09.16.05 Temperature, Heat, and Entropy
    3.012 Fundamentals of Materials Science Fall 2005 Lecture 4: 09.16.05 Temperature, heat, and entropy Today: LAST TIME .........................................................................................................................................................................................2� State functions ..............................................................................................................................................................................2� Path dependent variables: heat and work..................................................................................................................................2� DEFINING TEMPERATURE ...................................................................................................................................................................4� The zeroth law of thermodynamics .............................................................................................................................................4� The absolute temperature scale ..................................................................................................................................................5� CONSEQUENCES OF THE RELATION BETWEEN TEMPERATURE, HEAT, AND ENTROPY: HEAT CAPACITY .......................................6� The difference between heat and temperature ...........................................................................................................................6� Defining heat capacity.................................................................................................................................................................6�
    [Show full text]
  • Thermodynamics Formulation of Economics Burin Gumjudpai A
    Thermodynamics Formulation of Economics 306706052 NIDA E-THESIS 5710313001 thesis / recv: 09012563 15:07:41 seq: 16 Burin Gumjudpai A Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Economics (Financial Economics) School of Development Economics National Institute of Development Administration 2019 Thermodynamics Formulation of Economics Burin Gumjudpai School of Development Economics Major Advisor (Associate Professor Yuthana Sethapramote, Ph.D.) The Examining Committee Approved This Thesis Submitted in Partial 306706052 Fulfillment of the Requirements for the Degree of Master of Economics (Financial Economics). Committee Chairperson NIDA E-THESIS 5710313001 thesis / recv: 09012563 15:07:41 seq: 16 (Assistant Professor Pongsak Luangaram, Ph.D.) Committee (Assistant Professor Athakrit Thepmongkol, Ph.D.) Committee (Associate Professor Yuthana Sethapramote, Ph.D.) Dean (Associate Professor Amornrat Apinunmahakul, Ph.D.) ______/______/______ ABST RACT ABSTRACT Title of Thesis Thermodynamics Formulation of Economics Author Burin Gumjudpai Degree Master of Economics (Financial Economics) Year 2019 306706052 We consider a group of information-symmetric consumers with one type of commodity in an efficient market. The commodity is fixed asset and is non-disposable. We are interested in seeing if there is some connection of thermodynamics formulation NIDA E-THESIS 5710313001 thesis / recv: 09012563 15:07:41 seq: 16 to microeconomics. We follow Carathéodory approach which requires empirical existence of equation of state (EoS) and coordinates before performing maximization of variables. In investigating EoS of various system for constructing the economics EoS, unexpectedly new insights of thermodynamics are discovered. With definition of truly endogenous function, criteria rules and diagrams are proposed in identifying the status of EoS for an empirical equation.
    [Show full text]
  • Work and Energy Summary Sheet Chapter 6
    Work and Energy Summary Sheet Chapter 6 Work: work is done when a force is applied to a mass through a displacement or W=Fd. The force and the displacement must be parallel to one another in order for work to be done. F (N) W =(Fcosθ)d F If the force is not parallel to The area of a force vs. the displacement, then the displacement graph + W component of the force that represents the work θ d (m) is parallel must be found. done by the varying - W d force. Signs and Units for Work Work is a scalar but it can be positive or negative. Units of Work F d W = + (Ex: pitcher throwing ball) 1 N•m = 1 J (Joule) F d W = - (Ex. catcher catching ball) Note: N = kg m/s2 • Work – Energy Principle Hooke’s Law x The work done on an object is equal to its change F = kx in kinetic energy. F F is the applied force. 2 2 x W = ΔEk = ½ mvf – ½ mvi x is the change in length. k is the spring constant. F Energy Defined Units Energy is the ability to do work. Same as work: 1 N•m = 1 J (Joule) Kinetic Energy Potential Energy Potential energy is stored energy due to a system’s shape, position, or Kinetic energy is the energy of state. motion. If a mass has velocity, Gravitational PE Elastic (Spring) PE then it has KE 2 Mass with height Stretch/compress elastic material Ek = ½ mv 2 EG = mgh EE = ½ kx To measure the change in KE Change in E use: G Change in ES 2 2 2 2 ΔEk = ½ mvf – ½ mvi ΔEG = mghf – mghi ΔEE = ½ kxf – ½ kxi Conservation of Energy “The total energy is neither increased nor decreased in any process.
    [Show full text]
  • Thermodynamics
    ME346A Introduction to Statistical Mechanics { Wei Cai { Stanford University { Win 2011 Handout 6. Thermodynamics January 26, 2011 Contents 1 Laws of thermodynamics 2 1.1 The zeroth law . .3 1.2 The first law . .4 1.3 The second law . .5 1.3.1 Efficiency of Carnot engine . .5 1.3.2 Alternative statements of the second law . .7 1.4 The third law . .8 2 Mathematics of thermodynamics 9 2.1 Equation of state . .9 2.2 Gibbs-Duhem relation . 11 2.2.1 Homogeneous function . 11 2.2.2 Virial theorem / Euler theorem . 12 2.3 Maxwell relations . 13 2.4 Legendre transform . 15 2.5 Thermodynamic potentials . 16 3 Worked examples 21 3.1 Thermodynamic potentials and Maxwell's relation . 21 3.2 Properties of ideal gas . 24 3.3 Gas expansion . 28 4 Irreversible processes 32 4.1 Entropy and irreversibility . 32 4.2 Variational statement of second law . 32 1 In the 1st lecture, we will discuss the concepts of thermodynamics, namely its 4 laws. The most important concepts are the second law and the notion of Entropy. (reading assignment: Reif x 3.10, 3.11) In the 2nd lecture, We will discuss the mathematics of thermodynamics, i.e. the machinery to make quantitative predictions. We will deal with partial derivatives and Legendre transforms. (reading assignment: Reif x 4.1-4.7, 5.1-5.12) 1 Laws of thermodynamics Thermodynamics is a branch of science connected with the nature of heat and its conver- sion to mechanical, electrical and chemical energy. (The Webster pocket dictionary defines, Thermodynamics: physics of heat.) Historically, it grew out of efforts to construct more efficient heat engines | devices for ex- tracting useful work from expanding hot gases (http://www.answers.com/thermodynamics).
    [Show full text]
  • Thermodynamic Stability: Free Energy and Chemical Equilibrium ©David Ronis Mcgill University
    Chemistry 223: Thermodynamic Stability: Free Energy and Chemical Equilibrium ©David Ronis McGill University 1. Spontaneity and Stability Under Various Conditions All the criteria for thermodynamic stability stem from the Clausius inequality,cf. Eq. (8.7.3). In particular,weshowed that for anypossible infinitesimal spontaneous change in nature, d− Q dS ≥ .(1) T Conversely,if d− Q dS < (2) T for every allowed change in state, then the system cannot spontaneously leave the current state NO MATTER WHAT;hence the system is in what is called stable equilibrium. The stability criterion becomes particularly simple if the system is adiabatically insulated from the surroundings. In this case, if all allowed variations lead to a decrease in entropy, then nothing will happen. The system will remain where it is. Said another way,the entropyofan adiabatically insulated stable equilibrium system is a maximum. Notice that the term allowed plays an important role. Forexample, if the system is in a constant volume container,changes in state or variations which lead to a change in the volume need not be considered eveniftheylead to an increase in the entropy. What if the system is not adiabatically insulated from the surroundings? Is there a more convenient test than Eq. (2)? The answer is yes. To see howitcomes about, note we can rewrite the criterion for stable equilibrium by using the first lawas − d Q = dE + Pop dV − µop dN > TdS,(3) which implies that dE + Pop dV − µop dN − TdS >0 (4) for all allowed variations if the system is in equilibrium. Equation (4) is the key stability result.
    [Show full text]
  • Lecture 8: Maximum and Minimum Work, Thermodynamic Inequalities
    Lecture 8: Maximum and Minimum Work, Thermodynamic Inequalities Chapter II. Thermodynamic Quantities A.G. Petukhov, PHYS 743 October 4, 2017 Chapter II. Thermodynamic Quantities Lecture 8: Maximum and Minimum Work, ThermodynamicA.G. Petukhov,October Inequalities PHYS 4, 743 2017 1 / 12 Maximum Work If a thermally isolated system is in non-equilibrium state it may do work on some external bodies while equilibrium is being established. The total work done depends on the way leading to the equilibrium. Therefore the final state will also be different. In any event, since system is thermally isolated the work done by the system: jAj = E0 − E(S); where E0 is the initial energy and E(S) is final (equilibrium) one. Le us consider the case when Vinit = Vfinal but can change during the process. @ jAj @E = − = −Tfinal < 0 @S @S V The entropy cannot decrease. Then it means that the greater is the change of the entropy the smaller is work done by the system The maximum work done by the system corresponds to the reversible process when ∆S = Sfinal − Sinitial = 0 Chapter II. Thermodynamic Quantities Lecture 8: Maximum and Minimum Work, ThermodynamicA.G. Petukhov,October Inequalities PHYS 4, 743 2017 2 / 12 Clausius Theorem dS 0 R > dS < 0 R S S TA > TA T > T B B A δQA > 0 B Q 0 δ B < The system following a closed path A: System receives heat from a hot reservoir. Temperature of the thermostat is slightly larger then the system temperature B: System dumps heat to a cold reservoir. Temperature of the system is slightly larger then that of the thermostat Chapter II.
    [Show full text]
  • Entropy: Is It What We Think It Is and How Should We Teach It?
    Entropy: is it what we think it is and how should we teach it? David Sands Dept. Physics and Mathematics University of Hull UK Institute of Physics, December 2012 We owe our current view of entropy to Gibbs: “For the equilibrium of any isolated system it is necessary and sufficient that in all possible variations of the system that do not alter its energy, the variation of its entropy shall vanish or be negative.” Equilibrium of Heterogeneous Substances, 1875 And Maxwell: “We must regard the entropy of a body, like its volume, pressure, and temperature, as a distinct physical property of the body depending on its actual state.” Theory of Heat, 1891 Clausius: Was interested in what he called “internal work” – work done in overcoming inter-particle forces; Sought to extend the theory of cyclic processes to cover non-cyclic changes; Actively looked for an equivalent equation to the central result for cyclic processes; dQ 0 T Clausius: In modern thermodynamics the sign is negative, because heat must be extracted from the system to restore the original state if the cycle is irreversible . The positive sign arises because of Clausius’ view of heat; not caloric but still a property of a body The transformation of heat into work was something that occurred within a body – led to the notion of “equivalence value”, Q/T Clausius: Invented the concept “disgregation”, Z, to extend the ideas to irreversible, non-cyclic processes; TdZ dI dW Inserted disgregation into the First Law; dQ dH TdZ 0 Clausius: Changed the sign of dQ;(originally dQ=dH+AdL; dL=dI+dW) dHdQ Derived; dZ 0 T dH Called; dZ the entropy of a body.
    [Show full text]
  • Lecture 6: Entropy
    Matthew Schwartz Statistical Mechanics, Spring 2019 Lecture 6: Entropy 1 Introduction In this lecture, we discuss many ways to think about entropy. The most important and most famous property of entropy is that it never decreases Stot > 0 (1) Here, Stot means the change in entropy of a system plus the change in entropy of the surroundings. This is the second law of thermodynamics that we met in the previous lecture. There's a great quote from Sir Arthur Eddington from 1927 summarizing the importance of the second law: If someone points out to you that your pet theory of the universe is in disagreement with Maxwell's equationsthen so much the worse for Maxwell's equations. If it is found to be contradicted by observationwell these experimentalists do bungle things sometimes. But if your theory is found to be against the second law of ther- modynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation. Another possibly relevant quote, from the introduction to the statistical mechanics book by David Goodstein: Ludwig Boltzmann who spent much of his life studying statistical mechanics, died in 1906, by his own hand. Paul Ehrenfest, carrying on the work, died similarly in 1933. Now it is our turn to study statistical mechanics. There are many ways to dene entropy. All of them are equivalent, although it can be hard to see. In this lecture we will compare and contrast dierent denitions, building up intuition for how to think about entropy in dierent contexts. The original denition of entropy, due to Clausius, was thermodynamic.
    [Show full text]
  • The First Law of Thermodynamics Continued Pre-Reading: §19.5 Where We Are
    Lecture 7 The first law of thermodynamics continued Pre-reading: §19.5 Where we are The pressure p, volume V, and temperature T are related by an equation of state. For an ideal gas, pV = nRT = NkT For an ideal gas, the temperature T is is a direct measure of the average kinetic energy of its 3 3 molecules: KE = nRT = NkT tr 2 2 2 3kT 3RT and vrms = (v )av = = r m r M p Where we are We define the internal energy of a system: UKEPE=+∑∑ interaction Random chaotic between atoms motion & molecules For an ideal gas, f UNkT= 2 i.e. the internal energy depends only on its temperature Where we are By considering adding heat to a fixed volume of an ideal gas, we showed f f Q = Nk∆T = nR∆T 2 2 and so, from the definition of heat capacity Q = nC∆T f we have that C = R for any ideal gas. V 2 Change in internal energy: ∆U = nCV ∆T Heat capacity of an ideal gas Now consider adding heat to an ideal gas at constant pressure. By definition, Q = nCp∆T and W = p∆V = nR∆T So from ∆U = Q W − we get nCV ∆T = nCp∆T nR∆T − or Cp = CV + R It takes greater heat input to raise the temperature of a gas a given amount at constant pressure than constant volume YF §19.4 Ratio of heat capacities Look at the ratio of these heat capacities: we have f C = R V 2 and f + 2 C = C + R = R p V 2 so C p γ = > 1 CV 3 For a monatomic gas, CV = R 3 5 2 so Cp = R + R = R 2 2 C 5 R 5 and γ = p = 2 = =1.67 C 3 R 3 YF §19.4 V 2 Problem An ideal gas is enclosed in a cylinder which has a movable piston.
    [Show full text]
  • Adiabatic Bulk Moduli
    8.03 at ESG Supplemental Notes Adiabatic Bulk Moduli To find the speed of sound in a gas, or any property of a gas involving elasticity (see the discussion of the Helmholtz oscillator, B&B page 22, or B&B problem 1.6, or French Pages 57-59.), we need the “bulk modulus” of the fluid. This will correspond to the “spring constant” of a spring, and will give the magnitude of the restoring agency (pressure for a gas, force for a spring) in terms of the change in physical dimension (volume for a gas, length for a spring). It turns out to be more useful to use an intensive quantity for the bulk modulus of a gas, so what we want is the change in pressure per fractional change in volume, so the bulk modulus, denoted as κ (the Greek “kappa” which, when written, has a great tendency to look like k, and in fact French uses “K”), is ∆p dp κ = − , or κ = −V . ∆V/V dV The minus sign indicates that for normal fluids (not all are!), a negative change in volume results in an increase in pressure. To find the bulk modulus, we need to know something about the gas and how it behaves. For our purposes, we will need three basic principles (actually 2 1/2) which we get from thermodynamics, or the kinetic theory of gasses. You might well have encountered these in previous classes, such as chemistry. A) The ideal gas law; pV = nRT , with the standard terminology. B) The first law of thermodynamics; dU = dQ − pdV,whereUis internal energy and Q is heat.
    [Show full text]