Hesrpt: Optimal Scheduling of Parallel Jobs
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Shanlu › About › Cv › CV Shanlu.Pdf Shan Lu
Shan Lu University of Chicago, Dept. of Computer Science Phone: +1-773-702-3184 5730 S. Ellis Ave., Rm 343 E-mail: [email protected] Chicago, IL 60637 USA Homepage: http://people.cs.uchicago.edu/~shanlu RESEARCH INTERESTS Tool support for improving the correctness and efficiency of large scale software systems EMPLOYMENT 2019 – present Professor, Dept. of Computer Science, University of Chicago 2014 – 2019 Associate Professor, Dept. of Computer Sciences, University of Chicago 2009 – 2014 Assistant Professor, Dept. of Computer Sciences, University of Wisconsin – Madison EDUCATION 2008 University of Illinois at Urbana-Champaign, Urbana, IL Ph.D. in Computer Science Thesis: Understanding, Detecting, and Exposing Concurrency Bugs (Advisor: Prof. Yuanyuan Zhou) 2003 University of Science & Technology of China, Hefei, China B.S. in Computer Science HONORS AND AWARDS 2019 ACM Distinguished Member Among 62 members world-wide recognized for outstanding contributions to the computing field 2015 Google Faculty Research Award 2014 Alfred P. Sloan Research Fellow Among 126 “early-career scholars (who) represent the most promising scientific researchers working today” 2013 Distinguished Alumni Educator Award Among 3 awardees selected by Department of Computer Science, University of Illinois 2010 NSF Career Award 2021 Honorable Mention Award @ CHI for paper [C71] (CHI 2021) 2019 Best Paper Award @ SOSP for paper [C62] (SOSP 2019) 2019 ACM SIGSOFT Distinguished Paper Award @ ICSE for paper [C58] (ICSE 2019) 2017 Google Scholar Classic Paper Award for -
Software Engineering 0835
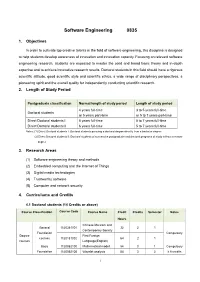
Software Engineering 0835 1. Objectives In order to cultivate top creative talents in the field of software engineering, this discipline is designed to help students develop awareness of innovation and innovation capacity. Focusing on relevant software engineering research, students are expected to master the solid and broad basic theory and in-depth expertise and to achieve innovative research results. Doctoral students in this field should have a rigorous scientific attitude, good scientific style and scientific ethics, a wide range of disciplinary perspectives, a pioneering spirit and the overall quality for independently conducting scientific research. 2. Length of Study Period Postgraduate classification Normal length of study period Length of study period 4 years full-time 3 to 5 years full-time Doctoral students or 5 years part-time or 5 to 7 years part-time Direct Doctoral students I 5 years full-time 5 to 7 years full-time Direct Doctoral students II 6 years full-time 5 to 7 years full-time Notes: (1) Direct Doctoral students I: Doctoral students pursuing a doctoral degree directly from a bachelor degree (2) Direct Doctoral students II: Doctoral students of successive postgraduate and doctoral programs of study without a master degree 3. Research Areas (1) Software engineering theory and methods (2) Embedded computing and the Internet of Things (3) Digital media technologies (4) Trustworthy software (5) Computer and network security 4. Curriculums and Credits 4.1 Doctoral students (14 Credits or above) Course Classification Course -
A ACM Transactions on Trans. 1553 TITLE ABBR ISSN ACM Computing Surveys ACM Comput. Surv. 0360‐0300 ACM Journal
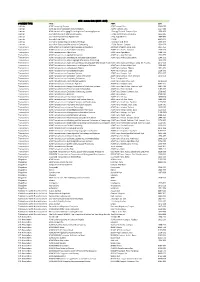
ACM - zoznam titulov (2016 - 2019) CONTENT TYPE TITLE ABBR ISSN Journals ACM Computing Surveys ACM Comput. Surv. 0360‐0300 Journals ACM Journal of Computer Documentation ACM J. Comput. Doc. 1527‐6805 Journals ACM Journal on Emerging Technologies in Computing Systems J. Emerg. Technol. Comput. Syst. 1550‐4832 Journals Journal of Data and Information Quality J. Data and Information Quality 1936‐1955 Journals Journal of Experimental Algorithmics J. Exp. Algorithmics 1084‐6654 Journals Journal of the ACM J. ACM 0004‐5411 Journals Journal on Computing and Cultural Heritage J. Comput. Cult. Herit. 1556‐4673 Journals Journal on Educational Resources in Computing J. Educ. Resour. Comput. 1531‐4278 Transactions ACM Letters on Programming Languages and Systems ACM Lett. Program. Lang. Syst. 1057‐4514 Transactions ACM Transactions on Accessible Computing ACM Trans. Access. Comput. 1936‐7228 Transactions ACM Transactions on Algorithms ACM Trans. Algorithms 1549‐6325 Transactions ACM Transactions on Applied Perception ACM Trans. Appl. Percept. 1544‐3558 Transactions ACM Transactions on Architecture and Code Optimization ACM Trans. Archit. Code Optim. 1544‐3566 Transactions ACM Transactions on Asian Language Information Processing 1530‐0226 Transactions ACM Transactions on Asian and Low‐Resource Language Information Proce ACM Trans. Asian Low‐Resour. Lang. Inf. Process. 2375‐4699 Transactions ACM Transactions on Autonomous and Adaptive Systems ACM Trans. Auton. Adapt. Syst. 1556‐4665 Transactions ACM Transactions on Computation Theory ACM Trans. Comput. Theory 1942‐3454 Transactions ACM Transactions on Computational Logic ACM Trans. Comput. Logic 1529‐3785 Transactions ACM Transactions on Computer Systems ACM Trans. Comput. Syst. 0734‐2071 Transactions ACM Transactions on Computer‐Human Interaction ACM Trans. -
ACM JOURNALS S.No. TITLE PUBLICATION RANGE :STARTS PUBLICATION RANGE: LATEST URL 1. ACM Computing Surveys Volume 1 Issue 1
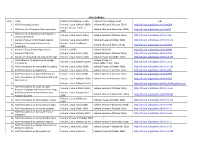
ACM JOURNALS S.No. TITLE PUBLICATION RANGE :STARTS PUBLICATION RANGE: LATEST URL 1. ACM Computing Surveys Volume 1 Issue 1 (March 1969) Volume 49 Issue 3 (October 2016) http://dl.acm.org/citation.cfm?id=J204 Volume 24 Issue 1 (Feb. 1, 2. ACM Journal of Computer Documentation Volume 26 Issue 4 (November 2002) http://dl.acm.org/citation.cfm?id=J24 2000) ACM Journal on Emerging Technologies in 3. Volume 1 Issue 1 (April 2005) Volume 13 Issue 2 (October 2016) http://dl.acm.org/citation.cfm?id=J967 Computing Systems 4. Journal of Data and Information Quality Volume 1 Issue 1 (June 2009) Volume 8 Issue 1 (October 2016) http://dl.acm.org/citation.cfm?id=J1191 Journal on Educational Resources in Volume 1 Issue 1es (March 5. Volume 16 Issue 2 (March 2016) http://dl.acm.org/citation.cfm?id=J814 Computing 2001) 6. Journal of Experimental Algorithmics Volume 1 (1996) Volume 21 (2016) http://dl.acm.org/citation.cfm?id=J430 7. Journal of the ACM Volume 1 Issue 1 (Jan. 1954) Volume 63 Issue 4 (October 2016) http://dl.acm.org/citation.cfm?id=J401 8. Journal on Computing and Cultural Heritage Volume 1 Issue 1 (June 2008) Volume 9 Issue 3 (October 2016) http://dl.acm.org/citation.cfm?id=J1157 ACM Letters on Programming Languages Volume 2 Issue 1-4 9. Volume 1 Issue 1 (March 1992) http://dl.acm.org/citation.cfm?id=J513 and Systems (March–Dec. 1993) 10. ACM Transactions on Accessible Computing Volume 1 Issue 1 (May 2008) Volume 9 Issue 1 (October 2016) http://dl.acm.org/citation.cfm?id=J1156 11. -

FCRC 2011 June 4 - 11, San Jose, CA TIMELINE SCHEDULE
FCRC 2011 June 4 - 11, San Jose, CA TIMELINE SCHEDULE Sponsored by Corporate Support Provided by Gold Silver CONFERENCE/WORKSHOP/EVENT ACRONYMS & DATES Dates Full Name Dates Full Name 3DAPAS 8 A Workshop on Dynamic Distrib. Data-Intensive Applications, Programming Abstractions, & Systs (HPDC) IWQoS 6--7 Int. Workshop on Quality of Service (ACM SIGMETRICS and IEEE Communications Society) A4MMC 4 Applications fo Multi and Many Core Processors: Analysis, Implementation, and Performance (ISCA) LSAP 8 P Workshop on Large-Scale System and Application Performance (HPDC) AdAuct 5 Ad Auction Workshop (EC) MAMA 8 Workshop on Mathematical Performance Modeling and Analysis (METRICS) AMAS-BT 4 P Workship on Architectural and Microarchitectural Support for Binary Translation (ISCA) METRICS 7--11 ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Systems BMD 5 Workshop on Bayesian Mechanism Design (EC) MoBS 5 A Workshop on Modeling, Benchmarking, and Simulation (ISCA) CARD 5 P Workshop on Computer Architecture Research Directions (ISCA) MRA 8 Int. Workshop on MapReduce and its Applications (HPDC) CBP 4 P JILP Workshop on Computer Architecture Competitions: Championship Branch Prediction (ISCA) MSPC 5 Memory Systems Performance and Correctness (PLDI) Complex 8--10 IEEE Conference on Computational Complexity (IEEE TCMFC) NDCA 5 A New Directions in Computer Architecture (ISCA) CRA-W 4--5 CRA-W Career Mentoring Workshop NetEcon 6 Workshop on the Economics of Networks, Systems, and Computation (EC) DIDC 8 P Int. Workshop on Data-Intensive Distributed Computing (HPDC) PLAS 5 Programming Languages and Analysis for Security Workshop (PLDI) EAMA 4 Workshop on Emerging Applications and Manycore Architectures (ISCA) PLDI 4--8 ACM SIGPLAN Conference on Programming Language Design and Implementation EC 5--9 ACM Conference on Electronic Commerce (ACM SIGECOM) PODC 6--8 ACM SIGACT-SIGOPT Symp. -

Curriculum Vitae
Caroline Trippel Assistant Professor of Computer Science and Electrical Engineering, Stanford University Stanford University Phone: (574) 276-6171 Computer Science Department Email: [email protected] 353 Serra Mall, Stanford, CA 94305 Home: https://cs.stanford.edu/∼trippel Education 2013–2019 Princeton University, PhD, Computer Science / Computer Architecture Thesis: Concurrency and Security Verification in Heterogeneous Parallel Systems Advisor: Prof. Margaret Martonosi 2013–2015 Princeton University, MA, Computer Science / Computer Architecture 2009–2013 Purdue University, BS, Computer Engineering PhD Dissertation Research Despite parallelism and heterogeneity being around for a long time, the degree to which both are being simultaneously deployed poses grand challenge problems in computer architecture regarding ensuring the accuracy of event orderings and interleavings in system-wide executions. As it turns out, event orderings form the cornerstone of correctness (e.g., memory consistency models) and security (e.g., speculation-based hardware exploits) in modern processors. Thus, my dissertation work creates formal, automated techniques for specifying and verifying the accuracy of event orderings for programs running on heterogeneous, parallel systems to improve their correctness and security. Awards and Honors [1] Recipient of the 2021 VMware Early Career Faculty Grant [2] Recipient of the 2020 CGS/ProQuest Distinguished Dissertation Award [3] Recipient of the 2020 ACM SIGARCH/IEEE CS TCCA Outstanding Dissertation Award [4] CheckMate chosen as an IEEE MICRO Top Pick of 2018 (top 12 computer architecture papers of 2018) [5] Selected for 2018 MIT Rising Stars in EECS Workshop [6] Selected for 2018 ACM Heidelberg Laureate Forum [7] TriCheck chosen as an IEEE MICRO Top Pick of 2017 (top 12 computer architecture papers of 2017) [8] NVIDIA Graduate Fellowship Recipient, Fall 2017–Spring 2018 [9] NVIDIA Graduate Fellowship Finalist, Fall 2016–Spring 2017 [10] Richard E. -

March 2, 2020 Remzi Arpaci-Dusseau Professor And
March 2, 2020 Remzi Arpaci-Dusseau Professor and Department Chair UW-Madison Computer Sciences With CC to Lance Potter for Department Files Dear Remzi: I write to formally request emeritus status upon my retirement from the University of Wisconsin-Madison this summer with my last day on the payroll being August 16, 2020. I started at Wisconsin on January 1, 1988. I believe that my 100000.1two years (32.5ten years) have been to both UW’s and my benefit. I feel blessed by my time at this great university. When I started, the following were non-existent or in niche use: world-wide web, laptops, broadband, and smartphones. Universities had no general email, course web pages, or social media presence. Companies like Amazon, Facebook, and Google could not exist. It has been a privilege to witness and modestly contribute to the last three decades of change by advancing computer hardware as the platform for information technology wizardry. On the next page to explain my research, I include the press release from my 2019 ACM - IEEE CS Eckert-Mauchly Award for seminal contributions to the fields of cache memories, memory consistency models, transactional memory, and simulation. It is the highest award in computer architecture and hardware and represents a lifetime of achievement. Note that “memory” refers to computer memory. On the final two pages, I summarize some of my UW accomplishments in the third person. Sincerely, Mark D. Hill John P. Morgridge Professor Gene M. Amdahl Professor of Computer Sciences Professor of Electrical and Computer Engineering (by courtesy) Chair of Computing Community Consortium (CCC) ACM Fellow & Fellow of the IEEE Eckert-Mauchly Award, 2019 CV: http://www.cs.wisc.edu/~markhill/markhill_cv.pdf Prof. -

PERMDNN: Efficient Compressed DNN Architecture with Permuted
PERMDNN: Efficient Compressed DNN Architecture with Permuted Diagonal Matrices Chunhua Deng∗+ Siyu Liao∗+ Yi Xie+ City University of New York City University of New York City University of New York [email protected] [email protected] [email protected] Keshab K. Parhi Xuehai Qian Bo Yuan+ University of Minnesota, Twin Cities University of Southern California City University of New York [email protected] [email protected] [email protected] Abstract—Deep neural network (DNN) has emerged as the demand intelligence, such as speech recognition [3], object most important and popular artificial intelligent (AI) technique. recognition [4], natural language processing [5] etc. The growth of model size poses a key energy efficiency challenge The extraordinary performance of DNNs with respect to for the underlying computing platform. Thus, model compression becomes a crucial problem. However, the current approaches are high accuracy is mainly attributed to their very large model limited by various drawbacks. Specifically, network sparsification sizes [6]–[8]. As indicated in a number of theoretical anal- approach suffers from irregularity, heuristic nature and large ysis [9] [10] and empirical simulations [11]–[13], scaling indexing overhead. On the other hand, the recent structured up the model sizes can improve the overall learning and matrix-based approach (i.e., CIRCNN) is limited by the rela- representation capability of the DNN models, leading to higher tively complex arithmetic computation (i.e., FFT), less flexible compression ratio, and its inability to fully utilize input sparsity. classification/predication accuracy than the smaller models. To address these drawbacks, this paper proposes PERMDNN, Motivated by these encouraging findings, the state-of-the-art a novel approach to generate and execute hardware-friendly DNNs continue to scale up with the purpose of tackling more structured sparse DNN models using permuted diagonal ma- complicated tasks with higher accuracy. -

ASPLOS XX Twentieth International Conference on Architectural Support for Programming Languages and Operating Systems
ASPLOS XX Twentieth International Conference on Architectural Support for Programming Languages and Operating Systems March 14–18, 2015 Istanbul, Turkey Sponsored by: ACM SIGARCH ACM SIGOPS ACM SIGPLAN In co-operation with: ACM SIGBED With Support from: Bilkent University, NSF, VMware, Intel, Google, ARM, Oracle, Microsoft Research, Facebook, IBM Research, and HP Labs The Association for Computing Machinery 2 Penn Plaza, Suite 701 New York, New York 10121-0701 Copyright © 2015 by the Association for Computing Machinery, Inc. (ACM). Permission to make digital or hard copies of portions of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyright for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, to republish, to post on servers or to redistribute to lists, requires prior specific permission and/or a fee. Request permission to republish from: [email protected] or Fax +1 (212) 869-0481. For other copying of articles that carry a code at the bottom of the first or last page, copying is permitted provided that the per-copy fee indicated in the code is paid through www.copyright.com. Notice to Past Authors of ACM-Published Articles ACM intends to create a complete electronic archive of all articles and/or other material previously published by ACM. If you have written a work that has been previously published by ACM in any journal or conference proceedings prior to 1978, or any SIG Newsletter at any time, and you do NOT want this work to appear in the ACM Digital Library, please inform [email protected], stating the title of the work, the author(s), and where and when published. -

Teaching Parallel Thinking to the Next Generation of Programmers
Teaching Parallel Thinking to the Next Generation of Programmers Brian Rague Computer Science, Weber State University Ogden, UT 84408, USA fronting multi-core development; programming ABSTRACT methodology was listed as the number one issue. The role of the application developer in the context Most collegiate programs in Computer Science of- of the multi-core environment is far from settled, fer an introductory course in programming, but two points can be stated with some certainty: primarily devoted to communicating the founda- tional principles of software design and develop- (1)Parallel and High Performance Computing (HPC) ment. Methodologies for solving problems within a as implemented on modern supercomputing plat- discrete computational context are presented. Lo- forms is not new, going back to vector computer gical thinking is highlighted, guided primarily by a systems in the latter half of the 1970s. [9] sequential approach to algorithm development and made manifest by typically using the latest, com- (2)Many computer science programs have tradition- mercially successful programming language. In re- ally viewed parallel programming as an advanced sponse to the most recent developments in ac- topic best suited for either graduate students or cessible multi-core computers, instructors of these Senior-level undergraduate students. introductory classes may wish to include training For some perspective on point (2) above, Pacheco on how to design workable parallel code. Novel is- [17] noted in his book published in 1997 that sues arise when programming concurrent applica- “most colleges and universities introduce parallel tions which can make teaching these concepts to programming in upper-division classes on com- beginning programmers a seemingly formidable puter architectures or algorithms.” Yet Wilkinson task. -

SIGARCH Annual Report July 2014 - June 2015
SIGARCH Annual Report July 2014 - June 2015 Overview The primary mission of SIGARCH continues to be the forum where researchers and practitioners of computer architecture can exchange ideas. SIGARCH sponsors or co-sponsors the premier conferences in the field as well as a number of workshops. It publishes a quarterly newsletter and the proceedings of several conferences. It is financially strong with a fund balance of over a million dollars. The SIGARCH bylaws are available online at http://www.acm.org/sigs/bylaws/arch_bylaws.html. Officers and Directors During the past fiscal year David Wood served as SIGARCH Chair, Sarita Adve served as Vice Chair, and Partha Ranganathan served as Secretary/Treasurer. Norm Jouppi, Kai Li, Scott Mahlke, and Per Stenstrom served on the Board of Directors, and Doug Burger also served as Past Chair. 2015 is an election year for SIGARCH; the current slate of elected officers is serving their second two-year term in accordance with SGB bylaws. In addition to these elected positions, there are three appointed positions. Doug DeGroot continues to serve as the Editor of the SIGARCH newsletter Computer Architecture News. Boris Grot has been appointed to serve as the SIGARCH Information Director, providing SIGARCH information online. Mattan Erez continues to serve as SIGARCH’s liaison on the SC conference steering committee. The election was delayed due to a combination of personal issues among the nomination committee— consisting of David Wood, Doug Burger, and Norm Jouppi—and difficulty getting qualified candidates to agree to run for the senior positions. The slate has been submitted and the election will be completed this summer. -

List of Related Organizations and Conferences
List of Related Organizations and Conferences Organization/Event Name Sponsor Description # of days With approx. 80,000 members, ACM delivers resources that advance computing as a science and a profession. ACM provides the computing field's premier Digital ACM Library and serves its members and the computing profession with leading-edge publications, conferences, and career resources. With nearly 85,000 members, the IEEE Computer Society is the world’s leading organization of computing professionals. Founded in 1946, and the largest of the IEEE Computer Society 39 societies of the Institute of Electrical and Electronics Engineers (IEEE), the CS is dedicated to advancing the theory and application of computer and information- processing technology. ASPLOS is a multi-disciplinary conference for research that spans the boundaries of hardware, computer architecture, compilers, languages, operating systems, networking, and applications. ASPLOS provides a high quality forum for scientists and engineers to present their latest research findings in these rapidly changing ASPLOS XIII ACM SIGARCH, SIGPLAN, SIGOPS 3 days fields. It has captured some of the major computer systems innovations of the past two decades (e.g., RISC and VLIW processors, small and large-scale multiprocessors, clusters and networks-of-workstations, optimizing compilers, RAID, and network-storage system designs). BSDCan, a BSD conference held in Ottawa, Canada, has quickly established itself as the technical conference for people working on and with 4.4BSD based operating BSDCanada 4 days systems and related projects. The organizers have found a fantastic formula that appeals to a wide range of people from extreme novices to advanced The Federated Computer Research Conference (FCRC) assembles a spectrum of affiliated research conferences and workshops into a week long coordinated meeting 7 day mix of held at a common time in a common place.