Tennessee State Library and Archives
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Water System Operator's Guide
MATH REVIEW For a rectangular tank: Most math problems a water treatment plant To find the capacity of a rectangular or square operator solves requires plugging numbers into tank: formulas and calculating the answer. When working with formulas, here are some simple Multiply length (L) by width (W) to get area (A). rules to follow. • Work from left to right. Multiply area by height (H) to get volume (V). • Do anything in parenthesis first. Multiply volume by 7.48 gallons per cubic foot to get capacity (C). • Do multiplication and division in the numerator (above the line) and in the A = L x W denominator (below the line), then do V = A x H addition and subtraction in the numerator C = V x 7.48 and denominator. • Divide the numerator by the denominator Find the capacity of a rectangular tank 15 feet (ft) last. long, 12 ft wide, and 10 ft high: Volume A = 15 ft x 12 ft = 180 square feet (ft2) The volume of a tank in cubic feet is equal to V = 180 ft2 x 10 ft = 1,800 cubic feet (ft3) the tank area multiplied by the tank height. The C = 1,800 ft3 x 7.48 gal/ft3 =13,464 gal capacity in gallons is equal to the volume in cubic feet multiplied by 7.48 gallons per cubic foot. For a circular tank: Area (A) = (3.14) x diameter squared (D2) / divided by 4 Volume (V) = A x H Capacity (C) = V x 7.48 gal/ft3 A = [ x (D2)/4] V = A x H C = V x 7.48 49 Find the capacity of a circular tank with a For an oval tank: diameter of 15 ft and a height of 12 ft: To find the gallons in an oval tank: A = [3.14 x (15 ft2)/4] = 177 ft2 Multiply the height by width by (3.14) divided by 4 to get the area of the oval. -

Estimating the Board Foot to Cubic Foot Ratio
United States Department of Agriculture Estimating the Forest Service Forest Board Foot to Products Laboratory Cubic Foot Ratio Research Paper FPL-RP-616 Steve Verrill Victoria L. Herian Henry Spelter Abstract Contents Certain issues in recent softwood lumber trade negotiations Page have centered on the method for converting estimates of 1 Introduction .................................................................... 1 timber volumes reported in cubic meters to board feet. Such conversions depend on many factors; three of the most im- 2 The F3 × F2 × F1 Model.................................................. 2 portant of these are log length, diameter, and taper. Average log diameters vary by region and have declined in the west- 3 The F1 Factor.................................................................. 2 ern United States due to the growing scarcity of large diame- ter, old-growth trees. Such a systematic reduction in size in 4 F3 × F2............................................................................. 3 the log population affects volume conversions from cubic units to board feet, which makes traditional rule of thumb 5 Applying the F3 × F2 × F1 Model to a Population conversion factors antiquated. In this paper we present an of West Coast Logs ........................................................ 3 improved empirical method for performing cubic volume to board foot conversions. 6 Smoothing the F3 × F2 Surface....................................... 4 Keywords: Scribner scaling, diameter, length, taper, 7 Optimal Smoothing -
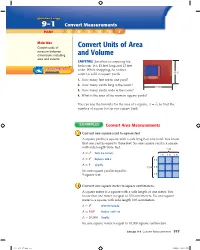
Convert Units of Area and Volume
Multi-Part Lesson 9-1 Convert Measurements PART A B C D E F Main Idea Convert units of Convert Units of Area measure between dimensions including and Volume area and volume. CARPETING Jonathan is carpeting his bedroom. It is 15 feet long and 12 feet wide. While shopping, he notices glencoe.com carpet is sold in square yards. 12 ft 1. How many feet are in one yard? 3 2. How many yards long is the room? 5 15 ft 3. How many yards wide is the room? 4 4. What is the area of the room in square yards? 20 yd2 You can use the formula for the area of a square,$" A = s2, to find the number of square feet in one square yard. Convert Area Measurements Convert one square yard to square feet. A square yard is a square with a side length of one yard. You know that one yard is equal to three feet. So, one square yard is a square with side length three feet. 1 yd A = s2 Write the formula. 1 ft 1 ft 1 ft 2 A = 3 Replace s with 3. 1 ft A = 9 Simplify. 1 yd 1 ft So, one square yard is equal to 9 square feet. 1 ft Convert one square meter to square centimeters. A square meter is a square with a side length of oneC09-014A-891643 meter. You know that one meter is equal to 100 centimeters. So, one square meter is a square with side length 100 centimeters. A = s2 Write the formula. -

The International System of Units (SI) - Conversion Factors For
NIST Special Publication 1038 The International System of Units (SI) – Conversion Factors for General Use Kenneth Butcher Linda Crown Elizabeth J. Gentry Weights and Measures Division Technology Services NIST Special Publication 1038 The International System of Units (SI) - Conversion Factors for General Use Editors: Kenneth S. Butcher Linda D. Crown Elizabeth J. Gentry Weights and Measures Division Carol Hockert, Chief Weights and Measures Division Technology Services National Institute of Standards and Technology May 2006 U.S. Department of Commerce Carlo M. Gutierrez, Secretary Technology Administration Robert Cresanti, Under Secretary of Commerce for Technology National Institute of Standards and Technology William Jeffrey, Director Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose. National Institute of Standards and Technology Special Publications 1038 Natl. Inst. Stand. Technol. Spec. Pub. 1038, 24 pages (May 2006) Available through NIST Weights and Measures Division STOP 2600 Gaithersburg, MD 20899-2600 Phone: (301) 975-4004 — Fax: (301) 926-0647 Internet: www.nist.gov/owm or www.nist.gov/metric TABLE OF CONTENTS FOREWORD.................................................................................................................................................................v -
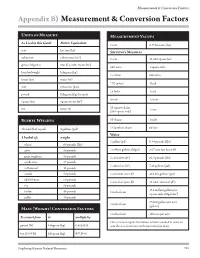
Appendix B) Measurement & Conversion Factors
Measurement & Conversion Factors Appendix B) Measurement & Conversion Factors Units of Measure Measurement Values As Used in this Guide Metric Equivalent 1 acre 2.47 hectares (ha) acre hectare (ha) Surveyor's Measures 3 cubic foot cubic meter (m ) 1 acre 43,560 square feet gallon/Mgallon liter (L), cubic meter (m3) 640 acres 1 square mile hundredweight kilogram (kg) 1 section 640 acres linear foot meter (m) 7.92 inches 1 link mile kilometer (km) 25 links 1 rod pound kilogram (kg) for mass 4 rods 1 chain square foot square meter (m2) 10 square chains ton tonne (t) 1 acre (160 square rods) Bushel Weights 80 chains 1 mile 1 bushel (bu) equals 8 gallons (gal) 1 Gunther's chain 66 feet Water 1 bushel of: weighs 1 gallon (gal) 8.34 pounds (lbs) wheat 60 pounds (lbs) corn 56 pounds 1 million gallons (Mgal) 3.07 acre feet (acre-ft) grain sorghum 56 pounds 1 cubic foot (ft3) 62.4 pounds (lbs) sunflowers 27 pounds 1 cubic foot (ft3) 7.48 gallons (gal) cottonseed 32 pounds canola 50 pounds 1 acre-foot (acre-ft) 325,851 gallons (gal) edible beans 60 pounds 1 acre-foot (acre-ft) 43,560 cubic feet (ft3) rye 56 pounds 17.4 million gallons per barley 48 pounds 1 inch of rain square mile (Mgal/mi2) millet 50 pounds 27,200 gallons per acre 1 inch of rain (gal/ac) Mass (Weight) Conversion Factors 1 inch of rain 100 tons per acre To convert from to multiply by One acre-foot equals the volume of water needed to cover an pound (lb) kilogram (kg) 0.4535924 area the size of one acre with water one foot deep. -

Explanation of Flow Rate
Explanation of Flow Rate Rate: Rate problems are any measured amount over another variable (a ratio). An example would be distance over time like miles per hour. It could be unit price of an item or a production rate. Rate problems are very common in all standardized math tests. Examples: $3 Unit Rate $3 per gallon is 1 gallon 80 miles 60 minutes 80 miles in 90 minutes is 90 minutes x 1 hour =53.3mph Flow rate is an amount of fluid traveling over time. It is a key concept when working with any fluids from medical to hydraulics. Here we are primarily looking at water flow rates. Flow rate is the amount of water (volume) over time. The amount of water moving through the system can be measured in one of three different units. They are gpm (gallons per minute), mgd (millions of gallons per day), and cfs (cubic feet per second). Example: Convert cfs to gallons per minute: 90 cf 7.5 gallons 60 seconds 90 cubic feet per second is sec x 1 cf X 1 minute =40,500 gallons per minute Instructional video on how to calculate flow rate The conversions are listed below. 7.5 gallons = 1 cubic foot 5280 feet = 1 mile 640 acres = 1 square mile 43560 square feet = 1 acre mgd x 700 = gpm cfs x 449 = gpm Example: A pipeline has a carrying capacity of 3 cfs. How many gpm can it handle? 3 cubic ft. 7.5 gallons 60 seconds 1350 gallons Solution: 1 second x 1 cubic foot x 1 minute = : minute Example: If the dimensions of California are approximately 220 miles wide and 740 miles long, what is the surface area in square miles of our state? Solution: SA = 220 miles x 740 miles = 162,800 square miles Example: If we had a state average annual rainfall of 30 inches, how many acre feet of water would that be? 640 acres 1 ft. -

Basic Information About Cubic Scaling
BASIC INFORMATION ABOUT CUBIC SCALING The primary reason for scaling logs is to establish log value, which is then used as a basis for payment. The most important secondary reason for scaling logs is to predict the quantity of end- products that can be recovered from a log. The major end-product produced from logs is lumber. Lumber is manufactured in a variety of sizes, each size having different applications. Besides lumber, additional end-products are produced from logs, each also having different applications. Veneer, chips, and sawdust are all used in the manufacture of many engineered lumber products plywood, oriented strand board (OSB), high-density particle board, etc. The predominant log scale rule used today Scribner decimal “C” does a pretty good job in reflecting log value, but has inherent limitations. Scribner predicts volume in board feet, based on boards that are one-inch thick, within a cylinder equal to the small-end log diameter. Other procedures become necessary to determine product recovery not predicted by the design of the Scribner decimal “C” log rule. Cubic scale does not predict a specific product volume. Instead of reflecting board feet, cubic scale reflects log volume in cubic measure. Since it doesn’t reflect a specific end-product, a cubic scale rule design can reflect volume differences due to varying log sizes and taper. The design of a cubic scale rule is based on a formula. The Smalian cubic log rule is one of the most common cubic measurement systems, probably because it is easy to use. As applied by the United States Forest Service in their Cubic Scaling Handbook, it reflects the volume of a log in cubic feet. -

Mulch Is Magic: Spread It!
MULCH IS MAGIC: SPREAD IT! MULCH IS MAGIC! How does mulch help our trees, shrubs and plants? keeps roots cool retains moisture protects roots from foot traffic protects trunk from lawn care equipment reduces erosion and soil compaction prevents water runoff improves the organic content of the soil absorbs excess moisture in spring and fall and extends the mud-free pavement zone, giving students more room to play keeps weeds down How much mulch do I need? Use the table below to calculate how much mulch you need. Mulch is ordered in cubic yards. (Note: the landscape and construction industry Why do we mulch? does not use metric). Spreading mulch around the base of The formula for volume is: V= Length x Width x Depth. trees and in gardens offers students a hands-on opportunity to learn about, and participate in, caring for If you measure and calculate volume in feet, divide your result by 27 to determine trees, shrubs and other plants. the number of cubic yards, since there are 27 cubic feet in one cubic yard (27 ft3 = 1 yd3). Students and stewardship If you measure and calculate volume in metres, multiply your result by 1.3 to For many years, students have been determine the number of cubic yards, since there are 1.3 cubic yards in 1 cubic planting gardens on their school 3 3 metre (1 m = 1.3 yd ). grounds and in local parks. While new projects are exciting, students Trees and shrubs: Recommended depth (spread mulch 6” (15 cm) deep). can learn a lot about environmental stewardship by caring for existing trees and gardens. -

Conversion Factors Length
Conversion Factors Length Multiply By To obtain Miles 1.60935 Kilometers 1,760 Yards 5,280 Feet 63,360 Inches Meters 0.00062137 Miles 1.0936 Yards 3.28088 Feet 39.37 Inches 100 Centimeters 0.001 Kilometers Yards 0.9144 Meters 0.00056818 Miles 3.0 Feet 36 Inches Feet 0.3048 Meters 0.00018939 Miles 0.33333 Yards 12 Inches Inches 0.08333 Feet 0.027778 Yards 0.000015783 Miles 2.54 Centimeters Area Square miles 4,014,489,600 Square inches 27,878,400 Square feet 3,097,600 Square yards 640 Acres 259 Hectares Acres 208.71 Square feet 0.404687 Hectares 0.0015625 Square miles 4,840 Square yards 43,560 Square feet 4,047 Square meters Square yards 0.83613 0.0000003228 Square miles 0.0002066 Acres 9 Square feet 1,296 Square inches Square feet 0.092903 Square meters 0.000000003587 Square miles 0.000022957 Acres 0.11111 Square yards 144 Square inches Square inches 0.0000000002491 Square miles 6.45163 Square centimeters 0.0000001594 Acres 0.0007716 Square yards 0.006944 Square feet Volume Acre-feet 325,851 U.S. gallons 43,560 Cubic feet 1,613.3 Cubic yards 1,233.49 Cubic meters Cubic yards 27 Cubic feet 46,656 Cubic inches 0.00061983 Acre-feet 0.76456 Cubic meters Cubic feet 1,728 Cubic inches 7.4805 U.S. gallons 28.317 Liters 0.037037 Cubic yards 0.000022957 Acre-feet C1 Conversion Factors (continued) Volume (continued) Multiply By To obtain U.S. gallons 231 Cubic inches 3.78543 Liters 0.13368 Cubic feet 0.00000307 Acre-feet Cubic inches 16.3872 Cubic centimeters 0.004329 U.S. -

Volume-To-Weight Conversion Factors
VOLUME-TO-WEIGHT CONVERSION FACTORS Materials: Volume * Weight in Pounds * PAPER: Mixed Paper Grades/Junk Mail, loose One cubic yard 875 Corrugated Cardboard (OCC), baled One cubic yard 1,100 Corrugated Cardboard (OCC), baled 30" x 60" x 48" 900 Corrugated Cardboard (OCC) , compacted One cubic yard 500 Corrugated Cardboard (OCC), flattened, loose 40 cubic yard roll-off 2000 Newsprint (ONP), loose One cubic yard 600 Newsprint (ONP), compacted One cubic yard 860 Newsprint (ONP) 12" stack 35 Office paper 40" x 48" x 40" 650) Office paper One cubic yard 400 Phone Books 12" stack 25 CONTAINERS: Mixed PET, dairy, whole loose One cubic yard 30 (Average) Mixed PET, dairy & other rigid, whole, loose One cubic yard 40 (Average) PET (soda bottles), whole, loose One cubic yard 35 PET (soda bottles), whole, loose Gaylord 45 PET (soda bottles), whole, baled 30" x 48" x 60" 600 HDPE (dairy only), baled 30" x 48" x 60" 650 HDPE (mixed), baled 30" x 48" x 60" 750 HDPE (whole) uncompacted One cubic yard 24 HDPE (whole) compacted One cubic yard 270 Aluminum Containers, whole One cubic yard 62 Aluminum Containers, flattened One cubic yard 250 Steel Cans, whole One cubic yard 150 Steel Cans, flattened One cubic yard 850 Glass Whole Containers One cubic yard 1,000 Glass Whole Container Full grocery bag 15 OTHER MATERIALS Scrap Metal One cubic yard 225 Scrap Metal--Used Major Appliances (average of all types and brands) One appliance 150 Pallets One, average size 35 Pallets Five cubic yards 2000 Electronic Scrap CRT (Computer Monitor) 50 Electronic Scrap TV -

Physics Concepts for Math 116
Physics concepts for Math 116 Here are, I think, all the physics concepts we will use in Math 116 this term. I won’t do them justice, of course; you should take Physics 140 for that. This is just a vocabulary cheat-sheet. I’ve included units for all the quantities, in both metric and English flavors. One of the best tricks the physicist has is to keep track of the units during a calculation. It’s a great way to check that your answer makes sense, and it catches a lot of mistakes. It helps a lot to be familiar with the conversions, especially the metric-to-metric conversions, like 1 N = 1 kg·m/s2. There are, of course, many more units for each quantity. I’ve just given a couple. I recom- mend the site http://www.onlineconversion.com/ if you want to convert units. Time Metric units: English units: seconds (s) seconds (s) Conversions: None needed Time you know. Length or Distance Metric units: English units: meters (m) feet (ft) Conversions: 1 m = 3.28 ft, 1 ft = .305 m, 1 in = 2.54 cm Length you know. One inch is exactly 2.54 centimeters. They redefined the inch to make that true. Area Metric units: English units: square meters (m2) square feet (ft2) Conversions: 1 m2 = 10.8 ft2, 1ft2 = .0929 m2 Area you know. Volume Metric units: English units: cubic meters (m3), liter (ℓ) cubic feet (ft3) Conversions: 1 m3 = 1000 ℓ, 1 m3 = 35.3 ft3, 1ft3 = .0283 m3 Volume you know. 1 Velocity Metric units: English units: meters per second (m/s) feet per second (ft/sec) Conversions: 1m/s = 3.28ft/s, 1ft/s = .305m/s Velocity is how fast some length or distance is changing. -

Tables of Basic Units of Weights and Measures Plastics Engineering
TABLES OF BASIC UNITS OF WEIGHTS AND MEASURES SI METRIC US CUSTOMARY Lengths 1 millimeter 0.03937 inch 1 centimeter 0.3937 inch 1 meter 39.37 inches or 1.0936 yards 1 kilometer 1039.61 yards or 0.6214 mile Area 1 square millimeter 0.00155 square inch 1 square centimeter 0.155 square inch 1 square meter 10.764 square feet or 1.196 square yards 1 square kilometer 0.3861 square mile Volumes 1 cubic millimeter 0.000061 cubic inch 1 cubic centimeter 0.061 cubic inch 1 liter 61.025 cubic inches 1 cubic meter 35.314 cubic feet or 264.173 gallons Weights 1 gram 0.03527 avoir. ounce or 15.4324 grains 1 kilogram (1000 gram) 2.2046 avoir. pounds US CUSTOMARY SI METRIC Length 1 inch 25.4 millimeters or 2.54 centimeters 1 foot 30.48 centimeters 1 yard 0.9144 meter 1 mile 1.6093 Kilometers Areas 1 square inch 645.16 square millimeters or 6.452 square centimeters 1 square foot 929.0341 square centimeters 1 square yard 8361.31 square centimeters 1 square mile 2.59 square kilometers Volume 1 cubic inch 16,387.2 cubic millimeters or 16.3872 cubic centimeters 1 cubic foot 28,317 cubic centimeters 1 cubic yard 0.7646 cubic meter Weights 1 grain 0.0648 gram 1 avoir. ounce 28.35 grams 1 avoir. pound 453.6 grams PLASTICS ENGINEERING COMPANY SHEBOYGAN, WISCONSIN 53082-0758 TABLES OF BASIC UNITS OF WEIGHTS AND MEASURES SI METRIC US CUSTOMARY Capacities 1 milliliter (0.001 liter) 0.0338 fluid ounce 1 liter 2.1134 liquid pint 1 liter 1.0567 liquid quart 1 liter 0.2642 gallon US CUSTOMARY SI METRIC Capacities 1 fluid ounce 29.573 milliliters 1 liquid pint 0.47317