DOCSLIB.ORG

Curvature Invariants for Wormholes and Warped Spacetimes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Curvature Invariants for Wormholes and Warped Spacetimes ABSTRACT Curvature Invariants for Wormholes and Warped Spacetimes B. Mattingly, Ph.D. Mentor: G. Cleaver, Ph.D. The Carminati and McLenaghan (CM) curvature invariants are powerful tools for probing spacetimes. Henry et al. formulated a method of plotting the CM curva- ture invariants to study black holes. The CM curvature invariants are scalar functions of the underlying spacetime. Consequently, they are independent of the chosen coor- dinates and characterize the spacetime. For Class B1 spacetimes, there are four inde- pendent CM curvature invariants: R, r1, r2, and w2. Lorentzian traversable wormholes and warp drives are two theoretical solutions to Einstein’s field equations, which allow faster-than-light (FTL) transport. The CM curvature invariants are plotted and an- alyzed for these specific FTL spacetimes: (i) the Thin-Shell Flat-Face wormhole, (ii) the Morris-Thorne wormhole, (iii) the Thin-Shell Schwarzschild wormhole, (iv) the arXiv:2103.14725v1 [gr-qc] 26 Mar 2021 exponential metric, (v) the Alcubierre metric at constant velocity, (vi) the Natário metric at constant velocity, and (vii) the Natário metric at an accelerating velocity. Plots of the wormhole CM invariants confirm their traversability and show how to distinguish the wormholes. The warp drive CM invariants reveal key features such as a flat harbor in the center of each warp bubble, a dynamic wake for each warp bubble, and rich internal structure(s) of each warp bubble. Copyright © 2021 by B. Mattingly All rights reserved TABLE OF CONTENTS LIST OF FIGURES ................................................................... vi LIST OF ABBREVIATIONS......................................................... x CHAPTER ONE Introduction ........................................................................ 1 1.1 Historical Foundations................................................... 1 1.2 Wormholes................................................................ 8 1.3 Warp Drives .............................................................. 10 1.4 Purpose of Research ..................................................... 12 CHAPTER TWO Curvature Invariants ............................................................... 15 2.1 Spacetime Manifolds ..................................................... 15 2.2 Curvature Invariants..................................................... 21 CHAPTER THREE Lorentzian Traversable Wormholes ............................................... 33 3.1 Thin-Shell Flat-Face Wormhole ......................................... 34 3.2 Morris-Thorne Wormhole ............................................... 36 3.3 Thin-Shell Schwarzschild Wormhole .................................... 43 3.4 Exponential Metric....................................................... 45 CHAPTER FOUR Warp Drives Moving at a Constant Velocity ..................................... 47 4.1 Warp Drive Spacetimes .................................................. 48 4.2 Alcubierre’s Warp Drive ................................................. 49 4.3 Natário’s Warp Drive.................................................... 66 CHAPTER FIVE Warp Drives Moving at a Constant Acceleration ................................ 78 5.1 The Accelerating Natário Spacetime .................................... 79 5.2 Invariant Plots of Time for Natário .................................... 82 5.3 Invariant Plots of Acceleration for Natário ............................ 88 5.4 Invariant Plots of Skin Depth for Natário ............................. 93 5.5 Invariant Plots of Radius for Natário .................................. 94 CHAPTER SIX Conclusion .......................................................................... 97 6.1 Invariant Research ....................................................... 99 6.2 Wormhole Research ......................................................102 iv 6.3 Warp Drive Research ....................................................104 6.4 Closing Thoughts.........................................................108 APPENDIX A Mathematica Program ............................................................. 111 APPENDIX B Invariants for the Natário Metric at Constant Velocity ......................... 122 APPENDIX C Invariants for the Natário Metric at Constant Acceleration..................... 130 BIBLIOGRAPHY ..................................................................... 133 v LIST OF FIGURES Figure 1.1. Figure 17.2 from [5]. It depicts the 2D analog of the time evolution of Eq. 1.2 rotated about the central vertical axis. ......... 4 Figure 1.2. Figure 17.3 from [5]. It depicts the full time evolution of Eq. 1.2.... 4 Figure 1.3. Figure 8.3 from [5]. It shows the null cone or light cone of events relative to P.............................................................. 6 Figure 1.4. An example of a tipping light cone by a warped underlying spacetime. ............................................................... 7 Figure 1.5. The light cone of an object rotating around the axis of a van Stockum spacetime will tip over........................................ 7 Figure 1.6. Fig. 1 from [11]. (a) is an embedding diagram for a wormhole that connects two different universes. (b) is an embedding diagram for a wormhole that connects two distant regions of our own universe. Each diagram depicts the geometry of an π equatorial (θ = 2 ) slice through space at a specific moment in time (t = constant). .................................................... 10 Figure 2.1. Figure 1.3.1 from [6]. ................................................... 17 Figure 2.2. Figure 1.3.2 from [6]. ................................................... 18 Figure 2.3. Figure 1.3.3 from [6]. ................................................... 19 Figure 3.1. Plots of the non-zero invariants for the MT wormhole. The plots are in radial coordinates with r 2 f0; 4g. Each radial mesh line represents a radial distance of r = 0:26¯. G = M = 1 were normalized for simplicity and r0 = 2 was chosen as the throat. Notice the divergence at the center of each plot is completely inside the r = 2 = r0 radial line. This does not affect the traversability of the wormhole. ........................................ 38 Figure 3.2. Successive plots of the shape function for different powers of r in the Ricci scalar for the MT wormhole. The plots are in radial coordinates with r 2 f0; 4g. Each radial mesh line represents a radial distance of r = 0:26¯. G = M = 1 were normalized for simplicity and r0 = 2 was chosen as the throat. ...................... 41 vi Figure 3.3. Plot of MT w2 for the shape function given in Eq. (3.11). The plots are in radial coordinates with r 2 f0; 4g with G = M = 1 normalized and r0 = 2 chosen. ......................................... 42 Figure 3.4. Plot of Schwarzschild w2. The plot is in radial coordinates with r 2 f0; 4g. Each mesh line represents a radial distance of 0:5. 3 The δ-function can be seen as a thin discontinuity at r = 2 and its value is recorded in Eq. (3.14). ..................................... 45 Figure 3.5. Plots of the non-zero invariants for the exponential metric. The plots are in radial coordinates with r 2 f0; 1:8Mg. Each mesh line represents a radial distance of 0:1M. The throat begins at r = M.................................................................... 46 Figure 4.1. The expansion of the normal volume elements for the Alcubierre warp drive spacetime.................................................... 49 Figure 4.2. Plots of the R invariants for the Alcubierre warp drive while varying a velocity. σ = 8 and ρ = 1 as Alcubierre originally suggested in his paper [32]. ............................................. 55 Figure 4.3. Plots of the r1 invariants for the Alcubierre warp drive while varying velocity. The other variables were chosen as σ = 8 and ρ = 1 to match the variables Alcubierre originally suggested in his paper [32]. ........................................................... 56 Figure 4.4. Plots of the w2 invariants for the Alcubierre warp drive while varying velocity. The radius was chosen as ρ = 1 to match the variables Alcubierre originally suggested in his paper [32]. The skin depth was chosen as σ = 2 to keep the plots as machine size numbers. Both velocity and skin depth have an exponential affect on the magnitude of the invariants.............................. 57 Figure 4.5. Plots of the R invariants for the Alcubierre warp drive while varying skin depth. The variables were chosen as vs = 8 and ρ = 1 to match the variables Alcubierre originally suggested in his paper [32]. ........................................................... 59 Figure 4.6. Plots of the r1 invariants for the Alcubierre warp drive while varying skin depth. The other variables were chosen as vs = 1 and ρ = 1 to match the variables Alcubierre originally suggested in his paper [32]. ........................................................ 60 Figure 4.7. Plots of the w2 invariants for the Alcubierre warp drive while varying skin-depth. The radius and velocity were chosen as ρ = 1 and vs = 1 to match the variables Alcubierre originally suggested in his paper [32]. ............................................. 61 vii Figure 4.8. Plots of the R invariants for the Alcubierre warp drive while varying radius. The other variables were chosen as σ = 8 and vs = 1 to match the variables Alcubierre originally suggested in his paper [32]. ........................................................... 63 Figure 4.9. Plots of the r1 invariants for the Alcubierre warp drive
Load more

Recommended publications
  • The Pentagon's UAP Task Force
    The Pentagon’s UAP Task Force Franc Milburn Mideast Security and Policy Studies No. 183 THE BEGIN-SADAT CENTER FOR STRATEGIC STUDIES BAR-ILAN UNIVERSITY Mideast Security and Policy Studies No. 183 The Pentagon’s UAP Task Force Franc Milburn The Pentagon’s UAP Task Force Franc Milburn © The Begin-Sadat Center for Strategic Studies Bar-Ilan University Ramat Gan 5290002 Israel Tel. 972-3-5318959 Fax. 972-3-5359195 [email protected] www.besacenter.org ISSN 0793-1042 November 2020 Cover image: Screen capture of US Navy footage of an Unidentified Aerial Phenomenon, US Department of Defense The Begin-Sadat (BESA) Center for Strategic Studies The Begin-Sadat Center for Strategic Studies is an independent, non-partisan think tank conducting policy-relevant research on Middle Eastern and global strategic affairs, particularly as they relate to the national security and foreign policy of Israel and regional peace and stability. It is named in memory of Menachem Begin and Anwar Sadat, whose efforts in pursuing peace laid the cornerstone for conflict resolution in the Middle East. Mideast Security and Policy Studies serve as a forum for publication or re-publication of research conducted by BESA associates. Publication of a work by BESA signifies that it is deemed worthy of public consideration but does not imply endorsement of the author’s views or conclusions. Colloquia on Strategy and Diplomacy summarize the papers delivered at conferences and seminars held by the Center for the academic, military, official and general publics. In sponsoring these discussions, the BESA Center aims to stimulate public debate on, and consideration of, contending approaches to problems of peace and war in the Middle East.
    [Show full text]
  • Star Trek.” Let’S Explore the Science of Space!
    Newspapers In Education and the Washington State Fair present BIG in the Future: STAR TREK AND SPACE “Star Trek: The Exhibition” is The Washington State Fair’s special exhibit featuring the science and technology behind the popular TV series, “Star Trek.” Let’s explore the science of space! SPEED: REALITY VS. FICTION If you’ve ever watched a video of a rocket launch, you’ll remember seeing enormous clouds of smoke and flmes as the spacecraft lifted off. The vessels in Star Trek, on the other hand, don’t have rocket engines and don’t shoot out hot exhaust gases. This is because in the show’s imagined future, scientists have made major breakthroughs in physics and propulsion. These advances—unknown to present science—allow a starship to “push” against something other than rocket exhaust. Known as warp drive, these fictional engines give starships the ability to travel at many times the speed of light. With warp drive, distances that would take tens of thousands of years to cover with today’s technology can be reached in just a few hours or days. A Star Trek-like propulsion system would make a lot of people very happy! IS ANYONE OUT THERE? When it comes to space, you’ll often encounter numbers so big that they give people headaches. It’s estimated that the visible universe has about 170,000,000,000 galaxies (the Milky Way being one of them) with a total of 300,000,000,000,000,000,000,000 stars between them (the sun being one of What qualities them).
    [Show full text]
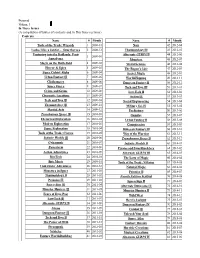
  • Pyramid Volume 3 in These Issues (A Compilation of Tables of Contents and in This Issue Sections) Contents Name # Month Tools Of
    Pyramid Volume 3 In These Issues (A compilation of tables of contents and In This Issue sections) Contents Name # Month Name # Month Tools of the Trade: Wizards 1 2008-11 Noir 42 2012-04 Looks Like a Job for… Superheroes 2 2008-12 Thaumatology III 43 2012-05 Venturing into the Badlands: Post- Alternate GURPS II 44 2012-06 3 2009-01 Apocalypse Monsters 45 2012-07 Magic on the Battlefield 4 2009-02 Weird Science 46 2012-08 Horror & Spies 5 2009-03 The Rogue's Life 47 2012-09 Space Colony Alpha 6 2009-04 Secret Magic 48 2012-10 Urban Fantasy [I] 7 2009-05 World-Hopping 49 2012-11 Cliffhangers 8 2009-06 Dungeon Fantasy II 50 2012-12 Space Opera 9 2009-07 Tech and Toys III 51 2013-01 Crime and Grime 10 2009-08 Low-Tech II 52 2013-02 Cinematic Locations 11 2009-09 Action [I] 53 2013-03 Tech and Toys [I] 12 2009-10 Social Engineering 54 2013-04 Thaumatology [I] 13 2009-11 Military Sci-Fi 55 2013-05 Martial Arts 14 2009-12 Prehistory 56 2013-06 Transhuman Space [I] 15 2010-01 Gunplay 57 2013-07 Historical Exploration 16 2010-02 Urban Fantasy II 58 2013-08 Modern Exploration 17 2010-03 Conspiracies 59 2013-09 Space Exploration 18 2010-04 Dungeon Fantasy III 60 2013-10 Tools of the Trade: Clerics 19 2010-05 Way of the Warrior 61 2013-11 Infinite Worlds [I] 20 2010-06 Transhuman Space II 62 2013-12 Cyberpunk 21 2010-07 Infinite Worlds II 63 2014-01 Banestorm 22 2010-08 Pirates and Swashbucklers 64 2014-02 Action Adventures 23 2010-09 Alternate GURPS III 65 2014-03 Bio-Tech 24 2010-10 The Laws of Magic 66 2014-04 Epic Magic 25 2010-11 Tools of the
    [Show full text]
  • I. Introduction
    A Simplified Guide To Rocket Science and Beyond – Understanding The Technologies of The Future Deep Bhattacharjee * , Sanjeevan Singha Roy Abstract : Rocket science has always been fairly complex. Its not because, it deals only the properties of rocket dynamics, attitude control, propulsion systems but the complexity arises mostly as a result of its payload, whether its manned or unmanned, how to make that payload reaches to orbit? How to a ssemble them in orbit to make giant structures like space stations? And most importantly, the mechanisms and aerodynamics of the shu t- tle associated with the lifting of the rocket. This paper , not only helps to make ease out the complex terminology, rigorou s mathematics, pain stro k- ing equations into a simplified norms, like a non - fiction for the general readers but also, no pre - requisite knowledge in the fi eld is needed to study this paper . However, every possible attempt have been make to simplify the dynam ics of rocket sciences and control mechanisms to the most easier way that one can imagine, still, there are some complex terminologies but pictures are provided deliberately with facts and h istories to boost up the way of understanding the subject much mor e better than before. It has been deliberately proved in this paper that rockets along with orbital m e- chanics, Kessler’s syndrome, Lunar and Martial landing of the Apollo and the Curiosity rovers, is not the future of the humanity to reach out to the stars . Therefore, to eliminate time completely, to warp the space in a new way, to make the gravity constant at 1g Earth gravity, physics of Ele c- trohydrodynamics – Or, the physics beyond the rocket propulsion by harnessing the Anti - Gravity is discussed in detai ls with various types of engines and experiments carried out throughout the globe.
    [Show full text]
  • Conformal Gravity and the Alcubierre Warp Drive Metric
    Physics Faculty Works Seaver College of Science and Engineering 2013 Conformal Gravity and the Alcubierre Warp Drive Metric Gabriele U. Varieschi Loyola Marymount University, [email protected] Zily Burstein Loyola Marymount University Follow this and additional works at: https://digitalcommons.lmu.edu/phys_fac Part of the Physics Commons Recommended Citation Gabriele U. Varieschi and Zily Burstein, “Conformal Gravity and the Alcubierre Warp Drive Metric,” ISRN Astronomy and Astrophysics, vol. 2013, Article ID 482734, 13 pages, 2013. doi: 10.1155/2013/482734 This Article is brought to you for free and open access by the Seaver College of Science and Engineering at Digital Commons @ Loyola Marymount University and Loyola Law School. It has been accepted for inclusion in Physics Faculty Works by an authorized administrator of Digital Commons@Loyola Marymount University and Loyola Law School. For more information, please contact [email protected]. Hindawi Publishing Corporation ISRN Astronomy and Astrophysics Volume 2013, Article ID 482734, 13 pages http://dx.doi.org/10.1155/2013/482734 Research Article Conformal Gravity and the Alcubierre Warp Drive Metric Gabriele U. Varieschi and Zily Burstein Department of Physics, Loyola Marymount University, Los Angeles, CA 90045, USA Correspondence should be addressed to Gabriele U. Varieschi; [email protected] Received 7 November 2012; Accepted 24 November 2012 Academic Editors: P. P. Avelino, R. N. Henriksen, and P. A. Hughes Copyright © 2013 G. U. Varieschi and Z. Burstein. is is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
    [Show full text]
  • Defense Intelligence Reference Document Warp Drive, Dark
    UNCLASSIFIED/ / FOR OFFICIAL USE ONLY Defense Intelligence Reference Document Acquisition Threat Support 2 2010 1 December 2009 DiA-08-1004-001 '------ Warp Drive, Dark Energy1 a11d the Manipulation of Dimensions UNCLASSIFIED//FOR OFFICIAL USE ONLY UNCLASSIFIED//FOR OFFICIAL USE ONLY Drive, Dark Energy, and the Manipulation of 1 Dimensions Prepared Acquisition Support Division (DW0-3) · Defense Warning Office Directorate for Analysis Defense Intelligence Agency Authors: Richard Obousy, Ph.D. President, Richard Obousy Consulting, LLC Eric W . Davis, Ph.D. Senior Research Physicist EarthTech International, Inc. Administrative Note COPYRIGHT WARNING: Further dissemination of the photogra.phs in tl1is is not authbrized. This product is one in series of advanced technology reports produced in FY 2009 under the Defense Intelligence Agency, Defense Warning Office's Advanced Aerospace Weapon System Applications (AAWSA) Program. Comments questions pertaining to th.is document should addressed to James Lacatski, D.Eng., AAWSA Program Manager, Defense Agency, CLAR/DW0-3, Bldg 6000, Washington, 20340-5100. ii UNCLASSIFIED/ /FOR OFFICIAL USE ONLY - --··--""·---·-·-""" .. UNCLASSIFIED/ /FOR OFFICIAL USE ONLY Contents Introduction .••..... " ...•........•••........•.•...•......•.......•......••., ....•.....•.•....•.••....• , ....•.•• •••..... v \ . 2. General Relativistic Warp Drives ....•. ;•·•············••··"'··" .• " .....•....: ..•.. ".".. " ·• ...• ). •..... 1 2.1 Warp Drive Requirements ..•.... ".""" •. """" •.•.• " .. " ..• "" •• " .•• ""."."
    [Show full text]
  • The Jeremiad in American Science Fiction Literature, 1890-1970
    University of Wisconsin Milwaukee UWM Digital Commons Theses and Dissertations May 2019 The eJ remiad in American Science Fiction Literature, 1890-1970 Matthew chneideS r University of Wisconsin-Milwaukee Follow this and additional works at: https://dc.uwm.edu/etd Part of the American Literature Commons, English Language and Literature Commons, and the United States History Commons Recommended Citation Schneider, Matthew, "The eJ remiad in American Science Fiction Literature, 1890-1970" (2019). Theses and Dissertations. 2119. https://dc.uwm.edu/etd/2119 This Dissertation is brought to you for free and open access by UWM Digital Commons. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of UWM Digital Commons. For more information, please contact [email protected]. THE JEREMIAD IN AMERICAN SCIENCE FICTION LITERATURE, 1890-1970 by Matthew J. Schneider A Dissertation Submitted in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy in English at The University of Wisconsin-Milwaukee May 2019 ABSTRACT THE JEREMIAD IN AMERICAN SCIENCE FICTION LITERATURE, 1890-1970 by Matthew J. Schneider The University of Wisconsin-Milwaukee, 2019 Under the Supervision of Professor Peter V. Sands Scholarship on the form of sermon known as the American jeremiad—a prophetic warning of national decline and the terms of promised renewal for a select remnant—draws heavily on the work of Perry Miller and Sacvan Bercovitch. A wealth of scholarship has critiqued Bercovitch’s formulation of the jeremiad, which he argues is a rhetorical form that holds sway in American culture by forcing political discourse to hold onto an “America” as its frame of reference.
    [Show full text]
  • Holographic Wormhole Drive: Philosophical Breakthrough in FTL 'Warp-Drive' Technology
    Holographic Wormhole Drive: Philosophical Breakthrough in FTL 'Warp-Drive' Technology Richard L. Amoroso Noetic Advanced Studies Institute Beryl, UT USA [email protected] Skeptics say Faster than light (FTL) space travel is the stuff of Science Fiction, could take 1,000 years and require a Jupiter size mass-energy source to operate superluminal warp drive spaceships. The author solves this problem in a radical new approach called the “Holographic Wormhole Drive” resulting in the possibility of warpdrive technologies in the near term. The Alcubierre warp drive metric (considered most advanced ) derived from Einstein’s General Relativity field equations by Miguel Alcubierre, in 1994 stretches space in a wave. Space ahead of a ship contracts & space behind expands, inhabitants of the warp-bubble travel along what astrophysicists call a ‘freefall’ geodesic, not moving locally inside the bubble at FTL velocities. But this model requires a negative mass-energy the size of Jupiter to operate. Amoroso uses a new spacetime transformation to cover the domain wall of the warp bubble with an array of mini-wormholes allowing an incursive oscillator to manipulate Alcubierre’s alpha and beta functions with minimal external energy input, i.e. the inherent infinite energy of the spacetime vacuum is used instead by a method of ‘ballistic’ spacetime programming. In "The Immanent Implementation of FTL Warp-Drive Technologies", from his book "Orbiting the Moons of Pluto, Amoroso solves major problems facing the Alcubierre metric based on principles of Holographic Anthropic Cosmology from another volume: "The Holographic Anthropic Multiverse". His solution is a 'Holographic Figure-Ground Effect' where the 'local' free-fall Warp Bubble separates from the holographic background by covering the domain wall of the free-fall warp-bubble with a system of mini-wormholes by 'programming mirror symmetry parameters of the spacetime vacuum'.
    [Show full text]
  • The Analysis of Harold White Applied to the Natario Warp Drive Spacetime
    The Analysis of Harold White applied to the Natario Warp Drive Spacetime. From 10 times the mass of the Universe to arbitrary low levels of negative energy density using a continuous Natario shape function with power factors.Warp Drives with two warped regions Fernando Loup To cite this version: Fernando Loup. The Analysis of Harold White applied to the Natario Warp Drive Spacetime. From 10 times the mass of the Universe to arbitrary low levels of negative energy density using a continuous Natario shape function with power factors.Warp Drives with two warped regions. 2013. hal-00844801 HAL Id: hal-00844801 https://hal.archives-ouvertes.fr/hal-00844801 Submitted on 15 Jul 2013 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. The Analysis of Harold White applied to the Natario Warp Drive Spacetime. From 10 times the mass of the Universe to arbitrary low levels of negative energy density using a continuous Natario shape function with power factors.Warp Drives with two warped regions Fernando Loup ∗ Residencia de Estudantes Universitas Lisboa Portugal July 15, 2013 Abstract Warp Drives are solutions of the Einstein Field Equations that allows superluminal travel within the framework of General Relativity.
    [Show full text]
  • Defense Intelligence Reference Document Warp Drive, Dark Energy
    UNCLASSIFIED//FOR OFFICIAL USE ONLY Defense Intelligence Reference Document Acquisition Threat Support 2 April 2010 ICOD: 1 December 2009 DiA-08-1004-001 ' .~ '----- Warp Drive, Dark Energy,a.,d the Manipulation of E~ra Dimensions UNCLASSIFIED/ / FOR OFFICIAL USE ONLY UNCLASSIFIED/ / FOR OFFICIAL USE ONLY Warp Drive, Dark Energy, and the Manipulation of Extr~ Dimensions I Prepared by : Acquisition Support Division (DWO- 3)' Defe nse W arning Office Directorate for Analysis Defense Intelligence Agency Authors: Richard K. Obousy, Ph.D. President, Richard Obousy Consulting, LLC Eric W . Davis, Ph. D. Senior Research Physicist EarthTech International, Inc. Administrative Not e COPYRIGHT WARNING : Further dissemination of the photographs in this publication is not authbrized. This product is one in a series of advanced technology reports produced in FY 2009 under the Defense Intelligence Agency, Defense Warning Office's Advanced Aerospace Weapon System Applications (AAWSA) Program. Comments or questions pertaining to this document should be addressed to James T. Lacatski, D.Eng., AAWSA Program Manager, Defense I ntelligence Agency, ATTN: CLAR/DWO-3, Bldg 6000, Washington, DC 20340-5100. ii UNCLASSIFIED/ / FOR OFFICIAL USE ONLY UNCLASSIFIED//FOR OFFICIAL USE ONLY Contents Introduction .••..... ., ...•........•••.. ., ....•.•...•......•.......•......••., ....•.....•.•....•.••....••....•.•• ~ •••..... v \ ' 2. General Relativistic Warp Drives ....•. ; •. ~ ..............; .. "' ..................: ..•..•..•.. " .•...• 1.. ..... 1 2.1 Warp Drive
    [Show full text]
  • Surfing on Top of a Gravitational Wave
    Global Journal of Science Frontier Research: A Physics and Space Science Volume 20 Issue 2 Version 1.0 Year 2020 Type : Double Blind Peer Reviewed International Research Journal Publisher: Global Journals Online ISSN: 2249-4626 & Print ISSN: 0975-5896 Surfing on Top of a Gravitational Wave By Stanislav Konstantinov Herzen State Pedagogical University Abstract- The article proposes, within the framework of the new cosmological model, which includes superfluid dark energy and dark matter, to revise the Einstein's “vacuum field equation” and, based on new astronomical observations, to refine the type and speed of gravitational waves. I note the need for further improve the LIGO and Virgo detectors for detecting longitudinal of gravitational waves. The article considers the Wakefield effect implemented in the AWAKE project for particle acceleration in the Large Hadron Collider as a mechanism for the possible acceleration of primary protons and spacecraft to superluminal speeds at the top of longitudinal gravitational waves in space. I suggest using the SMOLA plasma space engine to provide spacecraft energy in stationary and pulsed modes. Keywords: warp drive, gravitational wave, wakefield, surfing, proton, gamma radiation. GJSFR-A Classification: FOR Code: 020105 SurfingonTopofaGravitationalWave Strictly as per the compliance and regulations of: © 2020. Stanislav Konstantinov. This is a research/review paper, distributed under the terms of the Creative Commons Attribution-Noncommercial 3.0 Unported License http://creativecommons.org/licenses/by-nc/3.0/), permitting all non commercial use, distribution, and reproduction in any medium, provided the original work is properly cited. Surfing on Top of a Gravitational Wave Stanislav Konstantinov Abstract- The article proposes, within the framework of the new I.
    [Show full text]
  • Curvature Invariants for the Alcubierre and Natário Warp Drives
    universe Article Curvature Invariants for the Alcubierre and Natário Warp Drives Brandon Mattingly 1,2 , Abinash Kar 1,2 , Matthew Gorban 1,2, William Julius 1,2, Cooper K. Watson 1,2, MD Ali 1,2, Andrew Baas 1,2, Caleb Elmore 1,2 , Jeffrey S. Lee 1,2 , Bahram Shakerin 1,2, Eric W. Davis 1,3 and Gerald B. Cleaver 1,2,* 1 Early Universe Cosmology and Strings (EUCOS) Group, Center for Astrophysics, Space Physics and Engineering Research (CASPER), Baylor University, Waco, TX 76798, USA; [email protected] (B.M.); [email protected] (A.K.); [email protected] (M.G.); [email protected] (W.J.); [email protected] (C.K.W.); [email protected] (M.A.); [email protected] (A.B.); [email protected] (C.E.); [email protected] (J.S.L.); [email protected] (B.S.); [email protected] (E.W.D.) 2 Department of Physics, Baylor University, Waco, TX 76798, USA 3 Institute for Advanced Studies at Austin, 11855 Research Blvd., Austin, TX 78759, USA * Correspondence: [email protected] Abstract: A process for using curvature invariants is applied to evaluate the metrics for the Alcu- bierre and the Natário warp drives at a constant velocity. Curvature invariants are independent of coordinate bases, so plotting these invariants will be free of coordinate mapping distortions. As a consequence, they provide a novel perspective into complex spacetimes, such as warp drives. Warp drives are the theoretical solutions to Einstein’s field equations that allow for the possibility for faster-than-light (FTL) travel. While their mathematics is well established, the visualisation of Citation: Mattingly, B.; Kar, A.; such spacetimes is unexplored.
    [Show full text]