DOCSLIB.ORG

Chapter 7, Lesson 1 85

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 7, Lesson 1 85 Chapter 7, Lesson 1 85 Chapter 7, Lesson 1 18. They seem to be equal (and they seem to bisect each other). Set I (pages 260-261) Rhombuses. The aerial photographer Georg Gerster, the 19. They seem to be equal (and the opposite author of Below from Above (Abbeville Press, sides seem to be parallel). 1986), wrote about his photograph of the freeway overpass covered by carpets: 20. They seem to be perpendicular (and they "Years after having taken this photograph, I am seem to bisect each other). still amazed at this super-scale Paul Klee .... In Europe, special mats, a Swiss development, have •21. They are equiangular (or each of their been adopted. They retain the heat generated as angles is a right angle). the concrete hardens and make it unnecessary to 22. They are equilateral. keep wetting the concrete. The new procedure is more economical, though less colorful " Parallelograms. Theorem 24. 23. They seem to be parallel and equal. • 1. Two points determine a line. 24. They seem to be equal. 2. The sum of the angles of a triangle is 180°. 25. They seem to bisect each other. •3. Addition. SAT Problem. 4. Betweenness of Rays Theorem. •26. 2x + 2y = 180. (2x + 2y + 180 = 360.) 5. Substitution. 27. x + y = 90. Corollary. Set 11(pages 262-264) •6. The sum of the angles of a quadrilateral is Martin Gardner dedicated his book of mathemati• 360°. cal recreations, Penrose Tiles to Trapdoor Ciphers 7. Division. (W. H. Freeman and Company, 1989) to Roger Penrose with these words: 8. An angle whose measure is 90° is a right "To Roger Penrose, for his beautiful, surprising angle. discoveries in mathematics, physics, and •9. A quadrilateral each of whose angles is a cosmology; for his deep creative insights into right angle is a rectangle. how the universe operates; and for his humility in not supposing that he is exploring only the • 10. Each angle of a rectangle is a right angle. products of human minds." 11. All right angles are equal. Two chapters of Gardner's book are about Carpets. Penrose tilings, a subject full of rich mathematical ideas. The two tiles in the exercises come from a 12. Rectangles. rhombus with angles of 72° and 108°. John Norton Conway calls them "kites" and "darts." 13. Right. Amazingly, in all nonperiodic tilings of these tiles, •14. Lines that form right angles are perpen• the ratio of the number of kites to the number of dicular. darts is the golden ratio: = 1.618 ...! There 15. In a plane, two lines perpendicular to a third line are parallel. are a number of simple ways to prove that there are infinitely many ways to tile the plane with Rectangles. these two tiles. Even so, any finite region of one tiling appears infinitely many times in every other 16. They are equal and they are right angles. tiling; so no finite sample of a Penrose tiling can • 17. They seem to be parallel and equal. be used to determine which of the infinitely 86 Chapter 7, Lesson 1 nnany different tilings it is! Students interested in •40. Six sides, three diagorials, and four triangles. such mind-boggling ideas will enjoy reading Gardner's material and doing the experiments 41. Example figure: suggested in it. The exercises on the angles of polygons are intended to encourage students to realize that memorizing a result such as "each angle of an (n-2)i8o°„ equiangular n-gon has a measure of n is not important. What is important is for the student to feel comfortable and confident in being able to reconstruct such a result if it is 42. Eight sides, five diagonals, and six triangles. needed. •43. n-3. Penrose Tiles. 44. n-2. 28. The one labeled ABCD. 45. A quadrilateral has 4 - 3 = 1 diagonal which •29. 144°. (360°-3-72°.) forms 4-2 = 2 triangles. 30. •46. 720°. (4 X 180°.) 720° •47. 120°. (^.) 6 48. 1,080°. (6 X 180°.) 1 080° 49. 135°. (^^^.) • 31. SSS. 8 32. All are isosceles. 51. •50. (n-2)180°n . 33. They seem to be collinear. Linkage(n-2)180 Problems.° 34. They are collinear because •52. Their sum is 360°. ZACE = 72° + 108° = 180°. 53. Their sum is 180° if we think of the linkage 35. Yes. It appears that it could be folded along as a triangle. (It is 360° if we think of the the line through A, C, and E so that the two linkage as a quadrilateral, because halves would coincide. ZBCD = 180°.) 36. No. Quadrilateral ABED is equilateral but •54. They all appear to be smaller. not equiangular. 55. ZA + ZB + ZAPB = 180°, and Gentstone Pattern. ZC + ZD + ZCPD = 180°; so •37. Triangles, quadrilaterals, and an octagon. ZA + ZB + ZAPB = ZC + ZD + ZCPD. Because ZAPB = ZCPD, it follows that 38. Five sides, two diagonals, and three ZA + ZB = ZC + ZD by subtraction. triangles. Quadrilateral Angle Sum. 39. Example figure: 56. Addition. 57. Substitution. 58. Subtraction. Chapter 7, Lesson 2 87 59. Zl and Z2 are a linear pair; so they are 6. BC looks longer than CF, but they are supplementary and their sum is 180°. actually the same length. Likewise for Z3 and Z4. 7. The opposite angles of a parallelogram are (Zl + Z2) + (Z3 + Z4) = S; so equal. 180° + 180° = S, and so S = 360°. •8. An exterior angle of a triangle is greater Set III (page 264) than either remote interior angle. This triangle-to-square puzzle is the puzzle of 9. Substitution. Henry Dudeney first introduced in the Set III exercise of Chapter 1, Lesson 3. It is perhaps Theorem 26. surprising that, by carefully comparing the two 10. The opposite sides of a parallelogram are figures and knowing that the angles of an equal. equilateral triangle and a square are 60° and 90° respectively, we can find all of the remaining • 11. The opposite sides of a parallelogram are angles from just the one given. (By using the fact parallel. that the triangle and square have equal areas and 12. Parallel lines form equal alternate interior applying some simple trigonometry to the angles. triangle labeled D, we can find the exact values of all of the angles in the figure. The 41° angle, 13. ASA. 4/7 14. Corresponding parts of congruent triangles for example, is rounded from Arcsin —.) are equal. • 15. A line segment is bisected if it is divided into two equal segments. Point Symmetry. 16. •17. The diagonals of a parallelogram bisect each other. Chapter 7, Lesson 2 • 18. Two points are sjmimetric with respect to a point if it is the midpoint of the line segment Set I (pages 267-268) connecting them. 1. The first card (the card with the picture of 19. Parallel lines form equal alternate interior the baseball player). angles. •2. Point. 20. Vertical angles are equal. •3. See if the figure looks exactly the same 21. ASA. when it is turned upside down. 22. Corresponding parts of congruent triangles Optical Illusion. are equal. •4. Three. 23. Two points are symmetric with respect to a •5. Yes. The opposite sides of a parallelogram point if it is the midpoint of the line segment are equal. connecting them. 88 Chapter 7, Lesson 2 Set 11(pages 268-269) 34. Point E is the midpoint of AD. In encyclopedias and unabridged dictionaries, the •35. AD = 2DC. entry for "parallelogram" is followed by an entry for "parallelogram law." The Encyclopedia 36. They are supplementary. Parallel lines form Britannica describes it as the "rule for obtaining supplementary interior angles on the same geometrically the sum of two vectors by side of a transversal. constructing a parallelogram. A diagonal will give •37. 180. the requisite vector sum of two adjacent sides. The law is commonly used in physics to determine 38. 90. a resultant force or stress acting on a structure." The except from Newton's Mathematical Principles 39. Isosceles. of Natural Philosophy \s taken from the original 40. Right. Because x + y = 90, ZBEC = 90°. Latin edition published in 1687. It immediately follows statements of his three laws of motion. 41. BEIEC. A specific measure for ZBAD in the figure for Two Parallelograms. exercises 47 through 50 was given to make the exercises a little easier. Actually, an/measure other than 60° or 120° will work. A nice problem for better students would be to rework the exercises letting ZBAD = x°and to explain what happens when x = 60 or 120. Parallelogram Rule. 24. Corollary 43. Because x, y, and z are the measures of the angles of a triangle, x + y + z = 180. Therefore, ZABC is a straight angle; so A, B, and C are collinear. 44. Because ABDE and BCDE are parallelograms, AB II ED and BC II ED. If A, B, and C are not C D collinear, then through B there are two lines parallel to ED. This contradicts the Parallel •26. 10. (5 cm represents 50 lb; so 1 cm represents Postulate; so A, B, and C must be collinear. 10 lb.) •45. All three (AABE s ADEB = ABCD). 27. 25.(2.5x10 = 25.) 46. No. 28. About 6 cm. Hidden Triangles. 29. About 60. (6x10 = 60.) •30. About 24°. Angle Bisectors. 31. •32. ZAEB = :c°; ZCED = y° 48. AADE, ACDF, and AEBF. 33. AB,AE,andED. 49. SAS. Chapter 7, Lesson 3 89 50. Three. In addition to AABE and ABCF, ADEF Pop-Up Parallelogram. is equilateral because its sides are the • 1. A quadrilateral is a parallelogram if its corresponding sides of the three congruent triangles.
Load more

Recommended publications
  • Quadrilateral Theorems
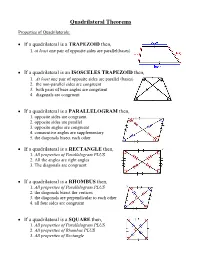
    Quadrilateral Theorems Properties of Quadrilaterals: If a quadrilateral is a TRAPEZOID then, 1. at least one pair of opposite sides are parallel(bases) If a quadrilateral is an ISOSCELES TRAPEZOID then, 1. At least one pair of opposite sides are parallel (bases) 2. the non-parallel sides are congruent 3. both pairs of base angles are congruent 4. diagonals are congruent If a quadrilateral is a PARALLELOGRAM then, 1. opposite sides are congruent 2. opposite sides are parallel 3. opposite angles are congruent 4. consecutive angles are supplementary 5. the diagonals bisect each other If a quadrilateral is a RECTANGLE then, 1. All properties of Parallelogram PLUS 2. All the angles are right angles 3. The diagonals are congruent If a quadrilateral is a RHOMBUS then, 1. All properties of Parallelogram PLUS 2. the diagonals bisect the vertices 3. the diagonals are perpendicular to each other 4. all four sides are congruent If a quadrilateral is a SQUARE then, 1. All properties of Parallelogram PLUS 2. All properties of Rhombus PLUS 3. All properties of Rectangle Proving a Trapezoid: If a QUADRILATERAL has at least one pair of parallel sides, then it is a trapezoid. Proving an Isosceles Trapezoid: 1st prove it’s a TRAPEZOID If a TRAPEZOID has ____(insert choice from below) ______then it is an isosceles trapezoid. 1. congruent non-parallel sides 2. congruent diagonals 3. congruent base angles Proving a Parallelogram: If a quadrilateral has ____(insert choice from below) ______then it is a parallelogram. 1. both pairs of opposite sides parallel 2. both pairs of opposite sides ≅ 3.
    [Show full text]
  • Properties of Equidiagonal Quadrilaterals (2014)
    Forum Geometricorum Volume 14 (2014) 129–144. FORUM GEOM ISSN 1534-1178 Properties of Equidiagonal Quadrilaterals Martin Josefsson Abstract. We prove eight necessary and sufficient conditions for a convex quadri- lateral to have congruent diagonals, and one dual connection between equidiag- onal and orthodiagonal quadrilaterals. Quadrilaterals with both congruent and perpendicular diagonals are also discussed, including a proposal for what they may be called and how to calculate their area in several ways. Finally we derive a cubic equation for calculating the lengths of the congruent diagonals. 1. Introduction One class of quadrilaterals that have received little interest in the geometrical literature are the equidiagonal quadrilaterals. They are defined to be quadrilat- erals with congruent diagonals. Three well known special cases of them are the isosceles trapezoid, the rectangle and the square, but there are other as well. Fur- thermore, there exists many equidiagonal quadrilaterals that besides congruent di- agonals have no special properties. Take any convex quadrilateral ABCD and move the vertex D along the line BD into a position D such that AC = BD. Then ABCD is an equidiagonal quadrilateral (see Figure 1). C D D A B Figure 1. An equidiagonal quadrilateral ABCD Before we begin to study equidiagonal quadrilaterals, let us define our notations. In a convex quadrilateral ABCD, the sides are labeled a = AB, b = BC, c = CD and d = DA, and the diagonals are p = AC and q = BD. We use θ for the angle between the diagonals. The line segments connecting the midpoints of opposite sides of a quadrilateral are called the bimedians and are denoted m and n, where m connects the midpoints of the sides a and c.
    [Show full text]
  • Midsegment of a Trapezoid Parallelogram
    Vocabulary Flash Cards base angles of a trapezoid bases of a trapezoid Chapter 7 (p. 402) Chapter 7 (p. 402) diagonal equiangular polygon Chapter 7 (p. 364) Chapter 7 (p. 365) equilateral polygon isosceles trapezoid Chapter 7 (p. 365) Chapter 7 (p. 402) kite legs of a trapezoid Chapter 7 (p. 405) Chapter 7 (p. 402) Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved. Vocabulary Flash Cards The parallel sides of a trapezoid Either pair of consecutive angles whose common side is a base of a trapezoid A polygon in which all angles are congruent A segment that joins two nonconsecutive vertices of a polygon A trapezoid with congruent legs A polygon in which all sides are congruent The nonparallel sides of a trapezoid A quadrilateral that has two pairs of consecutive congruent sides, but opposite sides are not congruent Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved. Vocabulary Flash Cards midsegment of a trapezoid parallelogram Chapter 7 (p. 404) Chapter 7 (p. 372) rectangle regular polygon Chapter 7 (p. 392) Chapter 7 (p. 365) rhombus square Chapter 7 (p. 392) Chapter 7 (p. 392) trapezoid Chapter 7 (p. 402) Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved. Vocabulary Flash Cards A quadrilateral with both pairs of opposite sides The segment that connects the midpoints of the parallel legs of a trapezoid PQRS A convex polygon that is both equilateral and A parallelogram with four right angles equiangular A parallelogram with four congruent sides and four A parallelogram with four congruent sides right angles A quadrilateral with exactly one pair of parallel sides Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved.
    [Show full text]
  • Cyclic Quadrilaterals
    GI_PAGES19-42 3/13/03 7:02 PM Page 1 Cyclic Quadrilaterals Definition: Cyclic quadrilateral—a quadrilateral inscribed in a circle (Figure 1). Construct and Investigate: 1. Construct a circle on the Voyage™ 200 with Cabri screen, and label its center O. Using the Polygon tool, construct quadrilateral ABCD where A, B, C, and D are on circle O. By the definition given Figure 1 above, ABCD is a cyclic quadrilateral (Figure 1). Cyclic quadrilaterals have many interesting and surprising properties. Use the Voyage 200 with Cabri tools to investigate the properties of cyclic quadrilateral ABCD. See whether you can discover several relationships that appear to be true regardless of the size of the circle or the location of A, B, C, and D on the circle. 2. Measure the lengths of the sides and diagonals of quadrilateral ABCD. See whether you can discover a relationship that is always true of these six measurements for all cyclic quadrilaterals. This relationship has been known for 1800 years and is called Ptolemy’s Theorem after Alexandrian mathematician Claudius Ptolemaeus (A.D. 85 to 165). 3. Determine which quadrilaterals from the quadrilateral hierarchy can be cyclic quadrilaterals (Figure 2). 4. Over 1300 years ago, the Hindu mathematician Brahmagupta discovered that the area of a cyclic Figure 2 quadrilateral can be determined by the formula: A = (s – a)(s – b)(s – c)(s – d) where a, b, c, and d are the lengths of the sides of the a + b + c + d quadrilateral and s is the semiperimeter given by s = 2 . Using cyclic quadrilaterals, verify these relationships.
    [Show full text]
  • Cyclic and Bicentric Quadrilaterals G
    Cyclic and Bicentric Quadrilaterals G. T. Springer Email: [email protected] Hewlett-Packard Calculators and Educational Software Abstract. In this hands-on workshop, participants will use the HP Prime graphing calculator and its dynamic geometry app to explore some of the many properties of cyclic and bicentric quadrilaterals. The workshop will start with a brief introduction to the HP Prime and an overview of its features to get novice participants oriented. Participants will then use ready-to-hand constructions of cyclic and bicentric quadrilaterals to explore. Part 1: Cyclic Quadrilaterals The instructor will send you an HP Prime app called CyclicQuad for this part of the activity. A cyclic quadrilateral is a convex quadrilateral that has a circumscribed circle. 1. Press ! to open the App Library and select the CyclicQuad app. The construction consists DEGH, a cyclic quadrilateral circumscribed by circle A. 2. Tap and drag any of the points D, E, G, or H to change the quadrilateral. Which of the following can DEGH never be? • Square • Rhombus (non-square) • Rectangle (non-square) • Parallelogram (non-rhombus) • Isosceles trapezoid • Kite Just move the points of the quadrilateral around enough to convince yourself for each one. Notice HDE and HE are both inscribed angles that subtend the entirety of the circle; ≮ ≮ likewise with DHG and DEG. This leads us to a defining characteristic of cyclic ≮ ≮ quadrilaterals. Make a conjecture. A quadrilateral is cyclic if and only if… 3. Make DEGH into a kite, similar to that shown to the right. Tap segment HE and press E to select it. Now use U and D to move the diagonal vertically.
    [Show full text]
  • Rhombus Rectangle Square Trapezoid Kite NOTES
    Geometry Notes G.9 Rhombus, Rectangle, Square, Trapezoid, Kite Mrs. Grieser Name: _________________________________________ Date: _________________ Block: _______ Rhombuses, Rectangles, Squares The Venn diagram below describes the relationship between different kinds of parallelograms: A rhombus is a parallelogram with four congruent sides A rectangle is a parallelogram with four right angles A square is a parallelogram with four congruent sides and four right angles Corollaries: A quadrilateral is a rhombus IFF it has four congruent sides A quadrilateral is a rectangles IFF it has four right angles A quadrilateral is a square IFF it is a rhombus and a rectangle. Since rhombuses, squares, and rectangles are parallelograms, they have all the properties of parallelograms (opposite sides parallel, opposite angles congruent, diagonals bisect each other, etc.) In addition… Rhombus Rectangle Square 4 congruent sides 4 right angles 4 congruent sides diagonals bisect angles diagonals congruent diagonals bisect each other diagonals perpendicular diagonals perpendicular 4 right angles diagonals congruent Theorems: A parallelogram is a rhombus IFF its diagonals are perpendicular. A parallelogram is a rhombus IFF each diagonal bisects a pair of opposite angles. A parallelogram is a rectangle IFF its diagonals are congruent. Examples: 1) Given rhombus DEFG, are the statements 2) Classify the parallelogram and find missing sometimes, always, or never true: values: a) b) a) D F b) D E c) DG GF 3) Given rhombus WXYZ 4) Given rectangle PQRS and and mXZY 34, find: mRPS 62 and QS=18, a) mWZV b) WY c) XY find: a) mQPR b) mPTQ c) ST Geometry Notes G.9 Rhombus, Rectangle, Square, Trapezoid, Kite Mrs.
    [Show full text]
  • Two-Dimensional Figures a Plane Is a Flat Surface That Extends Infinitely in All Directions
    NAME CLASS DATE Two-Dimensional Figures A plane is a flat surface that extends infinitely in all directions. A parallelogram like the one below is often used to model a plane, but remember that a plane—unlike a parallelogram—has no boundaries or sides. A plane figure or two-dimensional figure is a figure that lies completely in one plane. When you draw, either by hand or with a computer program, you draw two-dimensional figures. Blueprints are two-dimensional models of real-life objects. Polygons are closed, two-dimensional figures formed by three or more line segments that intersect only at their endpoints. These figures are polygons. These figures are not polygons. This is not a polygon A heart is not a polygon A circle is not a polygon because it is an open because it is has curves. because it is made of figure. a curve. Polygons are named by the number of sides and angles they have. A polygon always has the same number of sides as angles. Listed on the next page are the most common polygons. Each of the polygons shown is a regular polygon. All the angles of a regular polygon have the same measure and all the sides are the same length. SpringBoard® Course 1 Math Skills Workshop 89 Unit 5 • Getting Ready Practice MSW_C1_SE.indb 89 20/07/19 1:05 PM Two-Dimensional Figures (continued) Triangle Quadrilateral Pentagon Hexagon 3 sides; 3 angles 4 sides; 4 angles 5 sides; 5 angles 6 sides; 6 angles Heptagon Octagon Nonagon Decagon 7 sides; 7 angles 8 sides; 8 angles 9 sides; 9 angles 10 sides; 10 angles EXAMPLE A Classify the polygon.
    [Show full text]
  • Hexagon Fractions
    Hexagon Fractions A hexagon can be divided up into several equal, different-sized parts. For example, if we draw a line across the center, like this: We have separated the hexagon into two equal-sized parts. Each one is one-half of the hexagon. We could draw the lines differently: Here we have separated the hexagon into three equal-sized parts. Each one of these is one-third of the hexagon. 1 Another way of separating the hexagon into equal-sized parts looks like this: There are six equal-sized parts here, so each one is one-sixth of the hexagon. Each of these shapes has a special name. The shape that is one- half of the hexagon is called a trapezoid: The one that is one-third of the hexagon is a rhombus: 2 and the one that is one-sixth of the hexagon is a … Yes, a triangle! You knew that one, for sure. We can use these shapes to get an understanding of how fractions are added and subtracted. Remember that the numerator of a fraction is just a regular number. The denominator of a fraction is more than just a number, it is sort of a “thing,” like apple, dog, or flower. But it is a “numerical thing” and has a name. We should think of “half” or “third” or “tenth” or whatever as a name, just like “apple” or “dog” or “flower” is the name of something. The numerator in a fraction tells us how many of the denominators we have. For example, because the rhombus is one-third of a hexagon, we can think of the fraction “one-third” as “one rhombus.” For a hexagon, “third” and “rhombus” are two names for the same thing.
    [Show full text]
  • The Quad Squad Conjectures About Quadrilaterals
    2 The Quad Squad Conjectures About Quadrilaterals Warm Up Learning Goals Classify each figure using as • Use diagonals to draw quadrilaterals. many names as possible. • Make conjectures about the diagonals of 1. special quadrilaterals. • Make conjectures about the angle relationships of special quadrilaterals. • Categorize quadrilaterals based upon their properties. • Make conjectures about the midsegments 2. of quadrilaterals. • Understand that the vertices of cyclic quadrilaterals lie on the same circle. 3. Key Terms • coincident • isosceles trapezoid • interior angle of a • midsegment © Carnegie Learning, Inc. 4. polygon • cyclic quadrilateral • kite You have classifi ed quadrilaterals by their side measurements and side relationships. What conjectures can you make about diff erent properties of quadrilaterals? LESSON 2: The Quad Squad • M1-127 GGEO_SE_M01_T02_L02.inddEO_SE_M01_T02_L02.indd 112727 55/22/18/22/18 112:512:51 PPMM GETTING STARTED Cattywampus A quadrilateral may be convex or concave. The quadrilaterals you are most familiar with—trapezoids, parallelograms, rectangles, rhombi, and squares—are convex. For a polygon to be convex it contains all of the line segments connecting any pair of points. It is concave if and only if at least Think one pair of its interior angles is greater than 180°. about: Consider the two quadrilaterals shown. A quadrilateral has exactly two diagonals. Why can a concave quadrilateral have Convex Concave only one angle greater than 180°? 1. Draw the diagonals in the two quadrilaterals shown. What do you notice? 2. Make a conjecture about the diagonals of a convex quadrilateral and about the diagonals of a concave quadrilateral. The diagonals of any convex quadrilateral create two pairs of vertical angles © Carnegie Learning, Inc.
    [Show full text]
  • Properties of Special Parallelograms
    Project AMP Dr. Antonio Quesada – Director, Project AMP Properties of Special Parallelograms Lab Summary: This lab consists of four activities that lead students through the construction of a trapezoid. Students then explore the shapes, making conclusions about the angles, diagonals, and sides of the shapes. Key Words: trapezoid Background Knowledge: Students should be familiar with the basic geometry software commands. This lab does not provided step by step instructions for constructing a trapezoid. Therefore, students should understand that to construct a trapezoid, parallel lines must be constructed first to serve as the bases of a trapezoid. To construct the legs, students then must construct segments connecting the parallel lines. Learning Objectives: Students will identify the basic properties of trapezoids. Materials: Geometry software Suggested procedure: Split students into groups of two or three. Pass out worksheets Assessment: Check the completed worksheets and student constructions. Project AMP Dr. Antonio Quesada – Director, Project AMP Trapezoids Team members’ names: __________________________________________________ File name: ____________________________________________________________ Goal: Construct a trapezoid and analyze some of it properties. 1. This lab does not give you step by step instructions. Using your prior Cabri skills, construct a Trapezoid. The guidelines for a trapezoid are given below. A trapezoid has the following properties: · It is four sided · Two sides are parallel · Label the vertices K, L, M,
    [Show full text]
  • CAIU Polygons and Quadrilaterals
    CK-12 FOUNDATION CAIU Polygons and Quadrilaterals Hankes CK-12 Foundation is a non-profit organization with a mission to reduce the cost of textbook materials for the K-12 market both in the U.S. and worldwide. Using an open-content, web-based collaborative model termed the “FlexBook,” CK-12 intends to pioneer the generation and distribution of high-quality educational content that will serve both as core text as well as provide an adaptive environment for learning, powered through the FlexBook Platform™. Copyright © 2011 CK-12 Foundation, www.ck12.org Except as otherwise noted, all CK-12 Content (including CK-12 Curriculum Material) is made available to Users in accordance with the Creative Commons Attribution/Non-Commercial/Share Alike 3.0 Un- ported (CC-by-NC-SA) License (http://creativecommons.org/licenses/by-nc-sa/3.0/), as amended and updated by Creative Commons from time to time (the “CC License”), which is incorporated herein by this reference. Specific details can be found at http://www.ck12.org/terms. Printed: May 12, 2011 Author Wendy Hankes i www.ck12.org Contents 1 Angles in Polygons 1 1.1 Angles in Polygons ......................................... 1 2 Properties of Parallelograms 10 2.1 Properties of Parallelograms .................................... 10 3 Proving Quadrilaterals are Parallelograms 19 3.1 Proving Quadrilaterals are Parallelograms ............................ 19 4 Rectangles, Rhombuses 29 4.1 Rectangles, Rhombuses and Squares ............................... 29 5 Trapezoids and Kites 39 5.1 Trapezoids and Kites ........................................ 39 6 Quadrilaterals Review 53 6.1 Chapter 6 Review ......................................... 53 www.ck12.org ii Chapter 1 Angles in Polygons 1.1 Angles in Polygons Learning Objectives • Extend the concept of interior and exterior angles from triangles to convex polygons.
    [Show full text]
  • Area and Perimeter of Trapezoids
    Area and Perimeter of Trapezoids Bill Zahner Lori Jordan Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) AUTHORS Bill Zahner To access a customizable version of this book, as well as other Lori Jordan interactive content, visit www.ck12.org CK-12 Foundation is a non-profit organization with a mission to reduce the cost of textbook materials for the K-12 market both in the U.S. and worldwide. Using an open-content, web-based collaborative model termed the FlexBook®, CK-12 intends to pioneer the generation and distribution of high-quality educational content that will serve both as core text as well as provide an adaptive environment for learning, powered through the FlexBook Platform®. Copyright © 2013 CK-12 Foundation, www.ck12.org The names “CK-12” and “CK12” and associated logos and the terms “FlexBook®” and “FlexBook Platform®” (collectively “CK-12 Marks”) are trademarks and service marks of CK-12 Foundation and are protected by federal, state, and international laws. Any form of reproduction of this book in any format or medium, in whole or in sections must include the referral attribution link http://www.ck12.org/saythanks (placed in a visible location) in addition to the following terms. Except as otherwise noted, all CK-12 Content (including CK-12 Curriculum Material) is made available to Users in accordance with the Creative Commons Attribution-Non-Commercial 3.0 Unported (CC BY-NC 3.0) License (http://creativecommons.org/ licenses/by-nc/3.0/), as amended and updated by Creative Com- mons from time to time (the “CC License”), which is incorporated herein by this reference.
    [Show full text]