Hexagon Fractions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Square Rectangle Triangle Diamond (Rhombus) Oval Cylinder Octagon Pentagon Cone Cube Hexagon Pyramid Sphere Star Circle
SQUARE RECTANGLE TRIANGLE DIAMOND (RHOMBUS) OVAL CYLINDER OCTAGON PENTAGON CONE CUBE HEXAGON PYRAMID SPHERE STAR CIRCLE Powered by: www.mymathtables.com Page 1 what is Rectangle? • A rectangle is a four-sided flat shape where every angle is a right angle (90°). means "right angle" and show equal sides. what is Triangle? • A triangle is a polygon with three edges and three vertices. what is Octagon? • An octagon (eight angles) is an eight-sided polygon or eight-gon. what is Hexagon? • a hexagon is a six-sided polygon or six-gon. The total of the internal angles of any hexagon is 720°. what is Pentagon? • a plane figure with five straight sides and five angles. what is Square? • a plane figure with four equal straight sides and four right angles. • every angle is a right angle (90°) means "right ang le" show equal sides. what is Rhombus? • is a flat shape with four equal straight sides. A rhombus looks like a diamond. All sides have equal length. Opposite sides are parallel, and opposite angles are equal what is Oval? • Many distinct curves are commonly called ovals or are said to have an "oval shape". • Generally, to be called an oval, a plane curve should resemble the outline of an egg or an ellipse. Powered by: www.mymathtables.com Page 2 What is Cube? • Six equal square faces.tweleve edges and eight vertices • the angle between two adjacent faces is ninety. what is Sphere? • no faces,sides,vertices • All points are located at the same distance from the center. what is Cylinder? • two circular faces that are congruent and parallel • faces connected by a curved surface. -
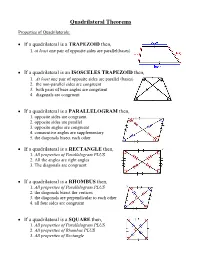
Quadrilateral Theorems
Quadrilateral Theorems Properties of Quadrilaterals: If a quadrilateral is a TRAPEZOID then, 1. at least one pair of opposite sides are parallel(bases) If a quadrilateral is an ISOSCELES TRAPEZOID then, 1. At least one pair of opposite sides are parallel (bases) 2. the non-parallel sides are congruent 3. both pairs of base angles are congruent 4. diagonals are congruent If a quadrilateral is a PARALLELOGRAM then, 1. opposite sides are congruent 2. opposite sides are parallel 3. opposite angles are congruent 4. consecutive angles are supplementary 5. the diagonals bisect each other If a quadrilateral is a RECTANGLE then, 1. All properties of Parallelogram PLUS 2. All the angles are right angles 3. The diagonals are congruent If a quadrilateral is a RHOMBUS then, 1. All properties of Parallelogram PLUS 2. the diagonals bisect the vertices 3. the diagonals are perpendicular to each other 4. all four sides are congruent If a quadrilateral is a SQUARE then, 1. All properties of Parallelogram PLUS 2. All properties of Rhombus PLUS 3. All properties of Rectangle Proving a Trapezoid: If a QUADRILATERAL has at least one pair of parallel sides, then it is a trapezoid. Proving an Isosceles Trapezoid: 1st prove it’s a TRAPEZOID If a TRAPEZOID has ____(insert choice from below) ______then it is an isosceles trapezoid. 1. congruent non-parallel sides 2. congruent diagonals 3. congruent base angles Proving a Parallelogram: If a quadrilateral has ____(insert choice from below) ______then it is a parallelogram. 1. both pairs of opposite sides parallel 2. both pairs of opposite sides ≅ 3. -

Second Grade C CCSS M Math Vo Ocabular Ry Word D List
Second Grade CCSS Math Vocabulary Word List *Terms with an asterisk are meant for teacher knowledge only—students do not need to learn them. Add To combine; put together two or more quantities. Addend Any number being added a.m. The half of the day from midnight to midday Analog clock Clock with hands: a clock that shows the time by means of hands on a dial Angle is formed by two rays with a common enndpoint (called the vertex) Array an orderly arrangement in rows and columns used in multiplication and division to show how multiplication can be shown as repeated addition and division can be shown as fair shares. *Associative Property of Addition When three or more numbers are added, the sum is the same regardless of the grouping of the addends. For example (2 + 3) + 4 = 2 + (3 + 4) Attribute A characteristic of an object such as color, shape, size, etc Bar graph A graph drawn using rectangular barrs to show how large each value is Bar Model a visual model used to solve word problems in the place of guess and check. Example: *Cardinality-- In mathematics, the cardinality of a set is a measure of the "number of elements of the set". For example, the set A = {2, 4, 6} contains 3 elements, and therefore A has a cardinality of 3. Category A collection of things sharing a common attribute Cent The smallest money value in many countries. 100 cents equals one dollar in the US. Centimeter A measure of length. There are 100 centimeters in a meter Circle A figure with no sides and no vertices. -

Applying the Polygon Angle
POLYGONS 8.1.1 – 8.1.5 After studying triangles and quadrilaterals, students now extend their study to all polygons. A polygon is a closed, two-dimensional figure made of three or more non- intersecting straight line segments connected end-to-end. Using the fact that the sum of the measures of the angles in a triangle is 180°, students learn a method to determine the sum of the measures of the interior angles of any polygon. Next they explore the sum of the measures of the exterior angles of a polygon. Finally they use the information about the angles of polygons along with their Triangle Toolkits to find the areas of regular polygons. See the Math Notes boxes in Lessons 8.1.1, 8.1.5, and 8.3.1. Example 1 4x + 7 3x + 1 x + 1 The figure at right is a hexagon. What is the sum of the measures of the interior angles of a hexagon? Explain how you know. Then write an equation and solve for x. 2x 3x – 5 5x – 4 One way to find the sum of the interior angles of the 9 hexagon is to divide the figure into triangles. There are 11 several different ways to do this, but keep in mind that we 8 are trying to add the interior angles at the vertices. One 6 12 way to divide the hexagon into triangles is to draw in all of 10 the diagonals from a single vertex, as shown at right. 7 Doing this forms four triangles, each with angle measures 5 4 3 1 summing to 180°. -

Properties of Equidiagonal Quadrilaterals (2014)
Forum Geometricorum Volume 14 (2014) 129–144. FORUM GEOM ISSN 1534-1178 Properties of Equidiagonal Quadrilaterals Martin Josefsson Abstract. We prove eight necessary and sufficient conditions for a convex quadri- lateral to have congruent diagonals, and one dual connection between equidiag- onal and orthodiagonal quadrilaterals. Quadrilaterals with both congruent and perpendicular diagonals are also discussed, including a proposal for what they may be called and how to calculate their area in several ways. Finally we derive a cubic equation for calculating the lengths of the congruent diagonals. 1. Introduction One class of quadrilaterals that have received little interest in the geometrical literature are the equidiagonal quadrilaterals. They are defined to be quadrilat- erals with congruent diagonals. Three well known special cases of them are the isosceles trapezoid, the rectangle and the square, but there are other as well. Fur- thermore, there exists many equidiagonal quadrilaterals that besides congruent di- agonals have no special properties. Take any convex quadrilateral ABCD and move the vertex D along the line BD into a position D such that AC = BD. Then ABCD is an equidiagonal quadrilateral (see Figure 1). C D D A B Figure 1. An equidiagonal quadrilateral ABCD Before we begin to study equidiagonal quadrilaterals, let us define our notations. In a convex quadrilateral ABCD, the sides are labeled a = AB, b = BC, c = CD and d = DA, and the diagonals are p = AC and q = BD. We use θ for the angle between the diagonals. The line segments connecting the midpoints of opposite sides of a quadrilateral are called the bimedians and are denoted m and n, where m connects the midpoints of the sides a and c. -

Ground and Explanation in Mathematics
volume 19, no. 33 ncreased attention has recently been paid to the fact that in math- august 2019 ematical practice, certain mathematical proofs but not others are I recognized as explaining why the theorems they prove obtain (Mancosu 2008; Lange 2010, 2015a, 2016; Pincock 2015). Such “math- ematical explanation” is presumably not a variety of causal explana- tion. In addition, the role of metaphysical grounding as underwriting a variety of explanations has also recently received increased attention Ground and Explanation (Correia and Schnieder 2012; Fine 2001, 2012; Rosen 2010; Schaffer 2016). Accordingly, it is natural to wonder whether mathematical ex- planation is a variety of grounding explanation. This paper will offer several arguments that it is not. in Mathematics One obstacle facing these arguments is that there is currently no widely accepted account of either mathematical explanation or grounding. In the case of mathematical explanation, I will try to avoid this obstacle by appealing to examples of proofs that mathematicians themselves have characterized as explanatory (or as non-explanatory). I will offer many examples to avoid making my argument too dependent on any single one of them. I will also try to motivate these characterizations of various proofs as (non-) explanatory by proposing an account of what makes a proof explanatory. In the case of grounding, I will try to stick with features of grounding that are relatively uncontroversial among grounding theorists. But I will also Marc Lange look briefly at how some of my arguments would fare under alternative views of grounding. I hope at least to reveal something about what University of North Carolina at Chapel Hill grounding would have to look like in order for a theorem’s grounds to mathematically explain why that theorem obtains. -

Petrie Schemes
Canad. J. Math. Vol. 57 (4), 2005 pp. 844–870 Petrie Schemes Gordon Williams Abstract. Petrie polygons, especially as they arise in the study of regular polytopes and Coxeter groups, have been studied by geometers and group theorists since the early part of the twentieth century. An open question is the determination of which polyhedra possess Petrie polygons that are simple closed curves. The current work explores combinatorial structures in abstract polytopes, called Petrie schemes, that generalize the notion of a Petrie polygon. It is established that all of the regular convex polytopes and honeycombs in Euclidean spaces, as well as all of the Grunbaum–Dress¨ polyhedra, pos- sess Petrie schemes that are not self-intersecting and thus have Petrie polygons that are simple closed curves. Partial results are obtained for several other classes of less symmetric polytopes. 1 Introduction Historically, polyhedra have been conceived of either as closed surfaces (usually topo- logical spheres) made up of planar polygons joined edge to edge or as solids enclosed by such a surface. In recent times, mathematicians have considered polyhedra to be convex polytopes, simplicial spheres, or combinatorial structures such as abstract polytopes or incidence complexes. A Petrie polygon of a polyhedron is a sequence of edges of the polyhedron where any two consecutive elements of the sequence have a vertex and face in common, but no three consecutive edges share a commonface. For the regular polyhedra, the Petrie polygons form the equatorial skew polygons. Petrie polygons may be defined analogously for polytopes as well. Petrie polygons have been very useful in the study of polyhedra and polytopes, especially regular polytopes. -

Right Triangles and the Pythagorean Theorem Related?
Activity Assess 9-6 EXPLORE & REASON Right Triangles and Consider △ ABC with altitude CD‾ as shown. the Pythagorean B Theorem D PearsonRealize.com A 45 C 5√2 I CAN… prove the Pythagorean Theorem using A. What is the area of △ ABC? Of △ACD? Explain your answers. similarity and establish the relationships in special right B. Find the lengths of AD‾ and AB‾ . triangles. C. Look for Relationships Divide the length of the hypotenuse of △ ABC VOCABULARY by the length of one of its sides. Divide the length of the hypotenuse of △ACD by the length of one of its sides. Make a conjecture that explains • Pythagorean triple the results. ESSENTIAL QUESTION How are similarity in right triangles and the Pythagorean Theorem related? Remember that the Pythagorean Theorem and its converse describe how the side lengths of right triangles are related. THEOREM 9-8 Pythagorean Theorem If a triangle is a right triangle, If... △ABC is a right triangle. then the sum of the squares of the B lengths of the legs is equal to the square of the length of the hypotenuse. c a A C b 2 2 2 PROOF: SEE EXAMPLE 1. Then... a + b = c THEOREM 9-9 Converse of the Pythagorean Theorem 2 2 2 If the sum of the squares of the If... a + b = c lengths of two sides of a triangle is B equal to the square of the length of the third side, then the triangle is a right triangle. c a A C b PROOF: SEE EXERCISE 17. Then... △ABC is a right triangle. -

M.EE.4.NF.1-2 Subject: Mathematics Number and Operations—Fractions (NF) Grade: 4
Mini-Map for M.EE.4.NF.1-2 Subject: Mathematics Number and Operations—Fractions (NF) Grade: 4 Learning Outcome DLM Essential Element Grade-Level Standard M.EE.4.NF.1-2 Identify models of one half (1/2) and one fourth M.4.NF.1 Explain why a fraction a/b is equivalent to a fraction (1/4). (n × a)/(n × b) by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. Use this principle to recognize and generate equivalent fractions. M.4.NF.2 Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as 1/2. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model. Linkage Level Descriptions Initial Precursor Distal Precursor Proximal Precursor Target Successor Communicate Divide familiar shapes, Divide familiar shapes, Identify the model that Identify the area model understanding of such as circles, such as circles, squares, represents one half or that is divided into "separateness" by triangles, squares, and/or rectangles, into one fourth of a familiar halves or fourths. recognizing objects that and/or rectangles, into two or more equal shape or object. are not joined together. two or more distinct parts. Communicate parts. These parts may understanding of or may not be equal. -

Cyclic Quadrilaterals — the Big Picture Yufei Zhao [email protected]
Winter Camp 2009 Cyclic Quadrilaterals Yufei Zhao Cyclic Quadrilaterals | The Big Picture Yufei Zhao [email protected] An important skill of an olympiad geometer is being able to recognize known configurations. Indeed, many geometry problems are built on a few common themes. In this lecture, we will explore one such configuration. 1 What Do These Problems Have in Common? 1. (IMO 1985) A circle with center O passes through the vertices A and C of triangle ABC and intersects segments AB and BC again at distinct points K and N, respectively. The circumcircles of triangles ABC and KBN intersects at exactly two distinct points B and M. ◦ Prove that \OMB = 90 . B M N K O A C 2. (Russia 1995; Romanian TST 1996; Iran 1997) Consider a circle with diameter AB and center O, and let C and D be two points on this circle. The line CD meets the line AB at a point M satisfying MB < MA and MD < MC. Let K be the point of intersection (different from ◦ O) of the circumcircles of triangles AOC and DOB. Show that \MKO = 90 . C D K M A O B 3. (USA TST 2007) Triangle ABC is inscribed in circle !. The tangent lines to ! at B and C meet at T . Point S lies on ray BC such that AS ? AT . Points B1 and C1 lies on ray ST (with C1 in between B1 and S) such that B1T = BT = C1T . Prove that triangles ABC and AB1C1 are similar to each other. 1 Winter Camp 2009 Cyclic Quadrilaterals Yufei Zhao A B S C C1 B1 T Although these geometric configurations may seem very different at first sight, they are actually very related. -

Cyclic Quadrilaterals
GI_PAGES19-42 3/13/03 7:02 PM Page 1 Cyclic Quadrilaterals Definition: Cyclic quadrilateral—a quadrilateral inscribed in a circle (Figure 1). Construct and Investigate: 1. Construct a circle on the Voyage™ 200 with Cabri screen, and label its center O. Using the Polygon tool, construct quadrilateral ABCD where A, B, C, and D are on circle O. By the definition given Figure 1 above, ABCD is a cyclic quadrilateral (Figure 1). Cyclic quadrilaterals have many interesting and surprising properties. Use the Voyage 200 with Cabri tools to investigate the properties of cyclic quadrilateral ABCD. See whether you can discover several relationships that appear to be true regardless of the size of the circle or the location of A, B, C, and D on the circle. 2. Measure the lengths of the sides and diagonals of quadrilateral ABCD. See whether you can discover a relationship that is always true of these six measurements for all cyclic quadrilaterals. This relationship has been known for 1800 years and is called Ptolemy’s Theorem after Alexandrian mathematician Claudius Ptolemaeus (A.D. 85 to 165). 3. Determine which quadrilaterals from the quadrilateral hierarchy can be cyclic quadrilaterals (Figure 2). 4. Over 1300 years ago, the Hindu mathematician Brahmagupta discovered that the area of a cyclic Figure 2 quadrilateral can be determined by the formula: A = (s – a)(s – b)(s – c)(s – d) where a, b, c, and d are the lengths of the sides of the a + b + c + d quadrilateral and s is the semiperimeter given by s = 2 . Using cyclic quadrilaterals, verify these relationships. -

2 Dimensional Figures
Study Island Copyright © 2021 Edmentum - All rights reserved. Generation Date: 07/26/2021 Generated By: Jennifer Fleming 1. An equilateral triangle is always an example of a/an: I. isosceles triangle II. scalene triangle III. right triangle A. I only B. II and III C. I and II D. II only 2. Which of the following is true about a parallelogram? Parallelograms always have four congruent sides. A. The diagonals of a parallelogram always bisect each other. B. Only two sides of a parallelogram are parallel. C. Opposite angles of a parallelogram are not congruent. D. 3. What is the difference between a rectangle and a rhombus? A rectangle has opposite sides parallel and a rhombus has no sides parallel. A. A rectangle has four right angles and a rhombus has opposite angles of equal measure. B. A rhombus has four right angles and a rectangle has opposite angles of equal measure. C. A rectangle has opposite sides of equal measure and a rhombus has no sides of equal measure. D. 4. What is a property of all rectangles? The four sides of a rectangle have equal length. A. The opposite sides of a rectangle are parallel. B. The diagonals of a rectangle do not have equal length. C. A rectangle only has two right angles. D. 5. An obtuse triangle is sometimes an example of a/an: I. scalene triangle II. isosceles triangle III. equilateral triangle IV. right triangle A. I or II B. I, II, or III C. III or IV D. II or III 6. What is the main difference between squares and rhombuses? Squares always have four interior angles which each measure 90°; rhombuses do not.