DOCSLIB.ORG

Wing-Strake Juncture

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Wing-Strake Juncture . c. 1 NASA Technical Paper 1803 .. .. I. - .~ ,. Experimental " and Analytical .Study. .. of the Longitudin al. Aero-dynamic . ~ , .- Characteristics of Analyticallyand -, - Configurations at.. -Subcritical Speeds .. John E. Lamar and ,Neal .T..Frink .~ TECH LIBRARY WFB, NY NASA TechnicalPaper 1803 Experimentaland Analytical Study of theLongitudinal Aerodynamic Characteristics of Analytically and Empirically Designed Strake- Wing Configurationsat Subcritical Speeds John E. Lamar and Neal T. Frink Latzgley ResearchCenter Humpton, Virgillia National Aeronautics and Space Administration Scientific and Technical Information Branch 1981 SUMMARY Sixteen analytically and empirically designed strakes havebeen tested experimentally on a wing-body at three subcritical speeds in such a way as toisolate thestrake-forebody loads from the wing-afterbody loads.Analyti- cal estimates for these longitudinal results havebeen made using thesuction analogy and the augmented vortex lift concepts. The comparisons show thatthe pitch data, both total and components, arebracketed well by the high- andlow- angle-of-attack modelings of thevortex lift theories. The lift dataare gener- ally better estimated by thehigh-angle-of-attack vortex lift theory and then only until maximum lift orstrake-vortex breakdown occurs over the wing. The compressibilityeffects noted in thedata for the strake-forebody lift are explained theoretically by a reduction in the wing upwash associated with increasing Machnumber which leadsto smaller potential and vortex lifts on the forward lifting surfaces. Aerodynamic synergism was investigatedexperimentally; as expected, there wasan additional lift benefit for all configurations as a result of the interaction. Furthermore, there was a delay in pitch-upassociated with the synergism. Machnumber has a small effect on the"additional lifting surface effi- ciencyfactor" whereas changes in thestrake geometry have largereffects. Geometry changes such asincreasing area orslenderness ratio generally pro- duce a more efficientstrake. However, it is possibleto obtain the larger values of this factor with approximatelyhalf the area of the original, also the largest,gothic strake by using a suitableanalytical design for the gothic leading edge. These resultscorrelate well with strake-vortex-breakdown observations in the water tunnel. Strake geometry is also important in determiningthe maximum lift that a configuration will develop, with gothic leading-edgeshaping being preferred for ratios of strakearea to wing referencearea of less than 0.25 based on the strakesconsidered herein. INTRODUCTION Strake-wing aerodynamics are becomingof increasinginterest due tothe mutual benefitsderived from the combination.(See ref. 1.) For the wing, thesebenefits include: (1) minimal interferenceat or below thecruise1 angle of attack, (2) upper-surface boundary-layer control at moderate to high angle lIn particular, at cruise it is possiblethat the small impact of the strake may only be attainable by the use ofcamber or dihedral so as to "unload" thestrake under this condition.Neither oneof these is addressed in this paper,as only planar strakes are considered. of attack due to the strake vortex, (3) load redistribution due to effective useof the upper surface, and (4) reduced area required for maneuver loads. For the strake, thesebenefits are: (1) strake vortexstrengthened by upwash from the mainwing and (2) the need foronly a small area - hence, wetted area andcomparatively lightweight structure - to generate its significant contri- bution to the total lift becausethe strake provideslarge amounts of vortex lift. Inview of these strake benefits, it is appropriate to consider how best to maximizethem by propershaping of the strake. One way would be to use an empiricalapproach based on previousknowledge, a second would be cut-and-try, a third would be analytical, and a fourth would be a combination of thepreced- ingthree. At the time ofdevelopment of the lightweightfighters F-16 and YF-17, onlythe first two procedures were available.After these airplanes were developed,reports were written,references 2 and 3, whichsummarized the wind-tunnel test results of about 100 different strakes foreach airplane, along with an analysis to helpguide future strake-wing integrations. However, thesereports still do notgive the aerodynamicist an analytical method for shapingthe strake leadingedge. One possible approachwould be to isolate some critical parameter,such as leading-edgesuction, and then design the strake inthe presence of the wing while monitoring this parameter. As a step in this direction, a simplerapproach with the emphasis on delayingstrake-vortex breakdown has been developed and reported inrefer- ence 4. There the shape of the isolated strake is determineduniquely in a flow which is simpler but related to thethree-dimensional potential by specifyingprimarily the leading-edgesuction distribution. Reference 4 reports the firstdesign application of this method in which the resulting shape was area scaled until the three-dimensional suction distribution over boththe strake and the wing was considered to be acceptable. Thewind- tunnel test of the strake-wingcombination showed it to perform well. How- ever, to determineif this method could be used to develop better strakes, it was applied to the developmentof over 200 configurations. Only 24 were consideredsuitable, or interesting enough, forfurther evaluation. These, alongwith 19 empiricallydesigned strakes mountedon the same wing-body, were tested, in a cooperativeprogram with the authors, in the Northrop 16- by 24-Inch Diagnostic Water Tunnel. From the results reported inreferences 5 and 6, only 16 strake-wingconfigurations, 7 analyticallydesigned and 9 empir- icallydesigned, were considered of sufficient interest to be tested on a similar wing-body in a wind tunnel.These tests, like those in water, were to be done at zerosideslip because of the large test matrixinvolved. It is recognizedthat the effects of sideslip and leading-and trailing-edge flaps are important with regard to vortex breakdownand the resulting amount of usefullift attainable; however,these effects are beyond the scope ofthe presentstudy. This report documents the wind-tunnel results and presentsthe analytical estimates forboth the complete configurations and thecomponents using the method described inreferences 1, 4, and 7. Use of trade names or names ofmanufacturers in this report does not constitute an officialendorsement of such products or manufacturers,either expressed or implied, by the NationalAeronautics andSpace Administration. SYMBOLS AND ABBREVIATIONS Dimensional quantities are given in both SI Units and U.S. CustomaryUnits. Measurementsand calculations were made in U.S. CustomaryUnits. AD analyticallydesigned b span (b, = 50.8 cm (20 in.)) C constantpressure specification in strake design Drag CD coefficient,drag - qSref cD,O experimentalvalue of drag coefficient at CL = 0 Lift CL liftcoefficient, - Gref CL,maxmaximum valueof CL,tot Cm pitching-momentcoefficient about 56.99 percent body lengthstation, Pitch ingmomen t qgrefcref kP lifting pressure coefficient CS leading-edgesuction-force coefficient, Kv, sin2le Leading-edgethrust CT leading-edgethrust-force coefficient, %$ref C chord, cm (in. ) - - C characteristiclength used determinationin of KVISe, cm (in.) Crefreference chord, 23.33 cm (9.185 in.) Section suction force CS sectionsuction-force coefficient, LC dFS differentialleading-edge suction force (see sketch D) dZ differentialleading-edge length ED empiricallydesigned 3 f additional lifting surface efficiency factor, a (Normal force/q,Sref) po tentia l lift factor,potential lift (KP in table IV) KP a(sin a cos a) KV vortex lift factor (KV in table IV) Kv, le leading-edgevortex lift factor, 1 a(IS.F-I le,left + Is-F-I Ie,right)~ " (KV LE in table IV) qmSre f a sin2 a Kv ,se side-edgevortex lift factor, (KV SE in table IV) KV,Z augmented vortex lift factor, (Kv, le/2) c (see appendix A) 1 distance along leading edgefrom apex, cm (in. ) M free-stream Machnumber P polynomial pressure specification in strakedesign qco free-stream dynamic pressure, N/m2 (lb/ft2) Ra ratio of exposed strakearea to wing referencearea, Ss/Sref Rb exposed semispan ratio, [(b/2)s/(b/2)w]exp RS strakeslenderness ratio, (Length/Semispan)e,p r radius of curvature, cm (in.) S area Sref reference wing area, 0.1032 m2 (1.1109 ft2) S.F. potential-flowsuction force CSC S - a2(b/2) U free-streamvelocity, m/sec (ft/sec) 4 ~ .. ._..... sum ofinduced downwash and Ua at a = 1 rad, m/sec (ft/sec) averagevalue of wnet, m/sec (f t/sec) local coordinatesdefining strake planform, cm (in.) (see 'table 111) locationof centroid of particular loading, cm (in.) locationof reference point from nose of model, 54.832 cm (21.587 in.) (X SUB REF in table IV) - = xref - xc,i, cm (in.) (i standsfor subscripts p, le, se, and se) angle of attack, deg (ALPHA intable IV) equivalentcirculation associated with leading-edge suction, m2/sec (ft2/sec) averagevalue of r (11, m2/sec (ft2/sec) fractionof exposed strake semispan leading-edgesweep angle, deg densityof fluid, kg/m3 (slugs/ft3) three-dimensional Subscripts : BD-TE strake vortex breakdown at wing trailing edge in water tunnel e XP exposed inb'd inboard le leadingedge max maximum outb' d outboard P potential r root S strake se sideedge - se augmented sideedge 5 swb strake-wing-bodyconfiguration tot total configuration vz e vortexeffect due to leadingedge vsevortex effect due to side edge - vsevortex effect due to augmented
Load more

Recommended publications
  • Vistara Soars Toward Expansion New Flight-Planning Technology Enhances Safety, Cuts Costs
    MOBILITY ENGINEERINGTM AUTOMOTIVE, AEROSPACE, OFF-HIGHWAY A quarterly publication of and Vistara soars toward expansion New flight-planning technology enhances safety, cuts costs Base-engine value engineering Deriving optimum efficiency, performance Autos & The Internet of Things How the IoT is disrupting the auto industry Software’s expanding role Escalating software volumes shifting design, systems integration Volume 3, Issue 2 June 2016 ME Molex Ad 0616.qxp_Mobility FP 4/28/16 5:00 PM Page 1 Support Tomorrow’s Speeds with Proven Connectivity Simply Solved In Automotive, consumer demand is changing even faster than technology. When you collaborate with Molex, we can develop a complete solution that will support tomorrow’s data speeds, backed by proven performance. Together, we can simplify your design and manufacturing processes — while minimizing space and maximizing connectivity throughout the vehicle. www.molex.com/a/connectedvehicle/in CONTENTS Features 40 Base-engine value engineering 49 Agility training for cars for higher fuel efficiency and AUTOMOTIVE CHASSIS enhanced performance Chassis component suppliers refine vehicle dynamics at AUTOMOTIVE POWERTRAIN the high end and entry level with four-wheel steering and adaptive damping. Continuous improvement in existing engines can be efficiently achieved with a value engineering approach. The integration of product development with value 52 Evaluating thermal design of engineering ensures the achievement of specified targets construction vehicles in a systematic manner and within a defined timeframe. OFF-HIGHWAY SIMULATION CFD simulation is used to evaluate two critical areas that 43 Integrated system engineering address challenging thermal issues: electronic control units for valvetrain design and and hot-air recirculation. development of a high-speed diesel engine AUTOMOTIVE POWERTRAIN The lead time for engine development has reduced significantly with the advent of advanced simulation Cover techniques.
    [Show full text]
  • United States Patent (19) 11) Patent Number: 4,691,879 Greene 45) Date of Patent: Sep
    United States Patent (19) 11) Patent Number: 4,691,879 Greene 45) Date of Patent: Sep. 8, 1987 54 JET AIRPLANE gravity. Full control of the airplane is possible under 76 Inventor: Vibert F. Greene, 19400 Sorenson high maneuverability conditions, extremely high accel Ave., Cupertino, Calif. 95014 erations and at large angles of attack. The delta nose wing creates swirling vortices that contribute substan 21 Appl. No.: 875,024 tially to the lift of the nose section. The winglet, an 22). Filed: Jun. 16, 1986 extension of the delta nose wing, allows the turbulent wake from the leading edge of the delta nose wing to 51 Int. Cl." .............................................. B64C39/08 flow over its upper surface to create additional lift while 52 U.S.C. .................................... 244/45 R; 24.4/13; the midspan wing causes the turbulent flow over its 244/45 A; 244/15 upper surface to form a turbulent wake at its leading 58 Field of Search .................. 244/45 R, 45 A, 4 R, edge. The V-tail delta wing with a V-shaped underside 244/15, 13 and blunt leading edge gives additional lift and control (56) References Cited to the airplane. A flow regulator helps to direct and U.S. PATENT DOCUMENTS control the flow field to the underside of the delta nose D. 138,538 8/1944 Clerc .................................. D12/331 wing and nose strake. There are eight pairs of control D. 155,569 10/1949 Bailey ............ ... D12/331 surfaces including an upper body stabilizer system for 3,447,76 6/1969 Whitener et al. ..................... 244/5 the control and stability of the airplane.
    [Show full text]
  • Water-Tunnel and Analytical Investigation of the Effect of Strake
    https://ntrs.nasa.gov/search.jsp?R=19800019803 2020-03-21T17:02:56+00:00Z NASA TP " 1676 NASA Technical Paper 1676 ,.,I c. 1 Water-Tunneland Analytical Investigation of the Effect of Strake Design Variables on Strake VortexBreakdown. Characteristics Neal T. Frink and John E. Lamar AUGUST 1980 TECH LIBRARY KAFB, NM NASA Technical Paper 1676 Water-Tunnel andAnalytical Investigation of the Effect of Strake Design Variables on Strake VortexBreakdown Characteristics Neal T. Frink andJohn E. Lamar Lavzgley Research Cetzter Haznptorz, Virgivzia National Aeronautics and Space Administration Scientific and Technical Information Branch 1980 SUMMARY A systematic water tunnel study was made to determine the vortex breakdown characteristics of43 strakes, more than half of which were generated from a new analytical strake design method. The strakes were mountedon a l/2-scale model of a Langley Research Center general research fighter fuselage mode1 with a 44O leading-edge-sweep trapezoidal wing. This study develops, in conjunction with a common wing-body, a parametric set of strake data for use in establishing and verifying a new strake design procedure. To develop this parametric data base, several series of isolated strakes were designedon the basis of a simplified approach which relates pre- scribed suction and pressure distributions in a simplified flow field to plan- form shapes. The resulting planform shapes provided examples of the effects of the pri- mary design parameters of size, span, and slenderness on the vortex breakdown characteristics. These effects are analyzed in relation to the respective strake leading-edge suction distributions. Included are examples of the effects of detailed strake planform shaping for strakes with the same general size and slenderness.
    [Show full text]
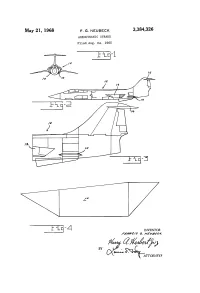
  • 4 INVENTOR 16%/6/S G
    May 21, 1968 F. G., NEUBECK 3,384,326 AERODYNAMIC STRAKE Filed Aug. 24, 1965 - E - - 4 INVENTOR 16%/6/s G. MazMayaea ... it is ATTORNEYsa 3,384,326 United States Patent Office Patented May 21, 1968 1. 2 bination of parts involved in the embodiment of the inven 3,384,326 tion as will appear from the following description and AERODYNAMC STRAKE accompanying drawings, wherein: Francis G. Neubeck, Eglin Air Force Base, Fla. FIG. 1 is a front elevation of the airplane showing the (94.67 Somerset Lane, Cypress, Calif. 90630) 5 angular relationship of the strakes in relation to the ver Filed Aug. 24, 1965, Ser. No. 482,304 tical axis of the airplane; 1 Claim. (CI. 244-13) FIG. 2 is a side elevation of the airplane showing the longitudinal position of a strake; FIG. 3 is an enlarged view of the rear portion of FIG. ABSTRACT OF THE DISCLOSURE 2, and showing with greater clarity the relationship be An elongated aerodynamic strake for use on an air 0 tween the aerodynamic strake and well-known airplane plane, and being in the form of a pentahedral prominence elements; and in plan and joined to and extending from each lower FIG. 4 is an enlarged plan view of the strake only. quarter aft section of the fuselage between the trailing The aerodynamic strake 10, constituting this invention, edge of the wing and the leading edge of the horizontal 5 is joined to the exterior of the fuselage skin on airplane stabilizer to be in the upwash area for improving overall 12, as shown on FIG.
    [Show full text]
  • Aerodynamic Design of the Strake for the Rocket Plane in Tailless Configuration
    AERODYNAMIC DESIGN OF THE STRAKE FOR THE ROCKET PLANE IN TAILLESS CONFIGURATION. M. Figat, A. Kwiek, K. Seneńko Warsaw University of Technology Keywords: Optimization, gradient method, strake, CFD Abstract of the MAS. Moreover, the Rocket Plane is able The paper presents results of the to fly at high angles of attack. It is assumed that, aerodynamic design of the Rocket Plane in a it should be equipped with a strake. tailless configuration. It is part of a Modular Airplane System - MAS. The system is devoted to the space tourism and the Rocket Plane is the main component of the system. The main goal of the research was improving aerodynamic characteristic of the Rocket Plane. The paper presents the proposal of modification of the initial Rocket Plane geometry which is being results from the optimization process. The final geometry of the Rocket Plane is resulting of a number of optimization. 1 Introduction Fig. 1 Concept of the MAS Space tourism is a very promising and fast developing branch of an aerospace technology The mission profile of the MAS is [1]. Especially the idea of suborbital tourist presented in Fig. 2. The mission profile of the flights is a very promising concept. The main MAS consists of the following five main advantage of this type of flights is a lower price phases: [1] compare to a tourist visit on the International Take-off Space Station. During a suborbital flight the Objects separation boundary between the Earth’s atmosphere and outer space is crossed, zero gravity condition Climbing and ballistic flight appears due to parabolic trajectory.
    [Show full text]
  • Effect of Wing Planform and Canard Location and Geometry on the of a Close-Coupled Canard Wing
    AND NASA TECHNICAL NOTE NASA TN D-7910 o-J WING PLANFORM N75-23514 -- (NASA-TN-D-7910)- EFFECT OF AND CANARD LOCATION AND GEOMETRY ON THE LONGITUDINAL AERODYNAMIC CHARACTERISTICS OF A CLOSE-COUPLED CANARD WING MODEL AT Unclas 1/02 23802 SUBSONIC SPEEDS (NASA) 86 pHC $.7,5 EFFECT OF WING PLANFORM AND CANARD LOCATION AND GEOMETRY ON THE LONGITUDINAL AERODYNAMIC CHARACTERISTICS OF A CLOSE-COUPLED CANARD WING MO[ AT SUBSONIC SPEEDS Blair B. Gloss C; .LT Langley Research Center 0T, Hampton, Va. 23665 16 .191 NATIONAL AERONAUTICS AND SPACE ADMINISTRATION * WASHINGTON,-D. * JUNE 1975 1. Report No. 2. Government Accession No. 3. Recipient's Catalog No. NASA TN D-7910 4. Title and Subtitle 5. Report Date EFFECT OF WING PLANFORM AND CANARD LOCATION June 1975 AND GEOMETRY ON THE LONGITUDINAL AERODYNAMIC CHARACTERISTICS OF A CLOSE-COUPLED CANARD WING MODEL AT SUBSONIC SPEEDS 7. Author(s) 8. Performing Organization Report No. L-9987 Blair B. Gloss 10. Work Unit No. 9. Performing Organization Name and Address 505-11-21-02 NASA Langley Research Center 11. Contract or Grant No. Hampton, Va. 23665 13. Type of Report and Period Covered 12. Sponsoring Agency Name and Address Technical Note National Aeronautics and Space Administration 14. Sponsoring Agency Code Washington, D.C. 20546 15. Supplementary Notes 16. Abstract A generalized wind-tunnel model with canard and wing planforms typical of highly maneu- verable aircraft was tested in the Langley 7- by 10-foot high-speed tunnel at a Mach number of 0.30 to determine the effect of canard location, canard size, wing sweep, and canard strake on canard-wing interference to high angles of attack.
    [Show full text]
  • Aiaa-98-4448 Application of Forebody Strakes For
    AIAA-98-4448 APPLICATION OF FOREBODY STRAKES FOR DIRECTIONAL STABILITY AND CONTROL OF TRANSPORT AIRCRAFT Gautam H. Shah* NASA Langley Research Center Hampton, VA J. Nijel Grandat The Boeing Company Long Beach, CA ABSTRACT during take-off, or high-crosswind landings. The resulting requirement for large vertical fin and rudder A brief overview of a cooperative area can exact a large cruise drag penalty, with an NASNBoeing research effort, Strake Technology associated increase in fuel cost. Therefore, alternate Research Application to Transport Aircraft (STRATA), methods which can provide the required directional intended to explore the potential of applying forebody stability and control during such critical situations strake technology to transport aircraft configurations for without resorting to large vertical taihdder area would directional stability and control at low angles of attack, be of great interest to aircraft manufacturers. is presented. As an initial step in the STRATA The use of forebody strakes for directional program, an exploratory wind-tunnel investigation of control of high-performance aircraft at high angles of the effect of fixed forebody strakes on the directional attack has been studied for quite some time, including stability and control characteristics of a generic transport ground and flight testing within NASA's High-Angle- configuration was conducted in the NASA Langley 12- of-Attack Technology Program (HATP). At high Foot Low-Speed Wind Tunnel. Results of parametric angles of attack (typically, a > 30"), crossflow on the variations in strake chord and span, as well as the effect forebody is substantial, and altering that flowfield can of strake incidence, are presented.
    [Show full text]
  • Technical Description
    TTEECCHHNNIICCAALL DDEESSCCRRIIPPTTIIOONN MMDD 990022 EEXXPPLLOORREERR MD Helicopters, Inc. Sales and Marketing 4555 E. McDowell Rd. Mesa, AZ 85215 PH: 480.346.6474 FAX: 480.346.6339 www.mdhelicopters.com [email protected] MISSION PROVEN, CHALLENGE READY THIS PAGE INTENTIONALLY LEFT BLANK TECHNICAL DESCRIPTION MD 902 EXPLORER MD Helicopters, Inc. 4555 E. McDowell Rd Mesa, Arizona CAGE: 1KVX4 DUNS: 054313767 www.mdhelicopters.com This Technical Description includes information and intellectual property that is the property of MD Helicopters, Inc. (MDHI). It provides general information for evaluation of the design, equipment, and performance of the MD 902 helicopter. The information presented in this Technical Description does not constitute an offer and is subject to change without notice. This proprietary information, in its entirety, shall not be duplicated, used, or disclosed—directly or indirectly, in whole or in part—for any purpose other than for evaluation. MD Helicopters, Inc. reserves the right to revise this Technical Description at any time MD 902 Explorer Technical Description REPORT NO.: MD14021407-902TD NO. OF PAGES: 74 Use or disclosure of data in this Technical Description is subject to the restriction on the cover page of this document. ATTACHMENTS: None Revision By Approved Date Pages and/or Paragraphs Affected New RCP 14-Feb-14 All (Initial Issue) MD 902 Explorer Technical Description Contents 1. FOREWORD ........................................................................................................ 1
    [Show full text]
  • The Effect of Tailboom Strakes and Vertical Fin Modifications on the Performance and Handling Qualities of OH-58 Helicopters
    University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Masters Theses Graduate School 5-2008 The Effect of Tailboom Strakes and Vertical Fin Modifications on the Performance and Handling Qualities of OH-58 Helicopters John A. Wade University of Tennessee - Knoxville Follow this and additional works at: https://trace.tennessee.edu/utk_gradthes Recommended Citation Wade, John A., "The Effect of Tailboom Strakes and Vertical Fin Modifications on the erP formance and Handling Qualities of OH-58 Helicopters. " Master's Thesis, University of Tennessee, 2008. https://trace.tennessee.edu/utk_gradthes/477 This Thesis is brought to you for free and open access by the Graduate School at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Masters Theses by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. To the Graduate Council: I am submitting herewith a thesis written by John A. Wade entitled "The Effect of Tailboom Strakes and Vertical Fin Modifications on the erP formance and Handling Qualities of OH-58 Helicopters." I have examined the final electronic copy of this thesis for form and content and recommend that it be accepted in partial fulfillment of the equirr ements for the degree of Master of Science, with a major in Aviation Systems. Richard Ranaudo, Major Professor We have read this thesis and recommend its acceptance: Stephen Corda, Uwe P. Solies Accepted for the Council: Carolyn R. Hodges Vice Provost and Dean of the Graduate School (Original signatures are on file with official studentecor r ds.) To the Graduate Council: I am submitting herewith a thesis written by John A.
    [Show full text]
  • The Discovery and Prediction of Vortex Flow Aerodynamics
    THE AERONAUTICAL JOURNAL JUNE 2019 VOLUME 123 NO 1264 729 pp 729–804. c Royal Aeronautical Society 2019.This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited. doi:10.1017/aer.2019.43 The discovery and prediction of vortex flow aerodynamics J.M. Luckring1 [email protected] NASA Langley Research Center Hampton, VA, USA ABSTRACT High-speed aircraft often develop separation-induced leading-edge vortices and vortex flow aerodynamics. In this paper, the discovery of separation-induced vortex flows and the devel- opment of methods to predict these flows for wing aerodynamics are reviewed. Much of the content for this article was presented at the 2017 Lanchester Lecture and the content was selected with a view towards Lanchester’s approach to research and development. Keywords: Aerodynamics; Vortex flow; Slender wings NOMENCLATURE AR aspect ratio, b2/S a similarity variable, α/tan() b wingspan CD drag coefficient CD,o minimum drag coefficient CD CD − CD,o CL lift coefficient CLα lift curve slope CL,p potential flow lift coefficient CL,v vortex flow lift coefficient Cm pitching moment coefficient Cp pressure coefficient Cp lifting pressure coefficient, Cp,l -Cp,u c wing chord cn section normal force coefficient cr root chord cs section suction coefficient ct tip chord 1 Senior Research Engineer, Configuration Aerodynamics Branch Received 27 January 2019; revised 6 March 2019; accepted 4 April 2019.
    [Show full text]
  • Investigation of Empennage Buffeting
    NASA Contractor Report 179426 Investigation of Empennage Buffeting C. Edward Lan and I. G. Lee Flight Research Laboratory The University of Kansas Center for Research, Inc. Lawrence, Kansas 66045 Appendix by William H. Wentz, Jr. Wichita State University Prepared for Ames Research Center Dryden Flight Research Facility Edwards, California Under Contract NAG2- 371 1987 N/ $A National Aeronautics and Space Administration Ames Research Center Dryden Flight Research Facility Edwards, California 93523- 5000 TABLE OF CONTENTS Page SUMMARY ......................................................... iii LIST OF SYMBOLS .................................................. iv I. INTRODUCTION ................................................. 1 2. THEORETICAL DEVELOPMENT ...................................... 3 2.1 Formulation of Equations ................................ 3 2.2 Existing Theoretical Methods for Buffet Prediction ..... I0 2.3 The Present Proposed Method ............................ 17 3. NUMERICAL RESULTS ........................................... 25 3.1 Results for a 65-degree Delta Wing ..................... 26 3.2 Results for an F-18 Configuration ...................... 27 4. CONCLUSIONS AND RECOMMENDATIONS ............................. 30 5. REFERENCES .................................................. 31 APPENDIX: Water Tunnel Studies of Vortex Flow and Vortex-Fin Interaction on the F/A-18 Aircraft ......... 51 PRECEDING pAGE BLANK NOT FILMED [ii LIST OF SYMBOLS the generalized aerodynamic force matrix Anj - f/ Cpj% bending moment
    [Show full text]
  • Computational Study of Flow Interactions Over a Close Coupled Canard-Wing on Fighter
    International Journal of Aviation, Aeronautics, and Aerospace Volume 6 Issue 1 Article 5 2019 Computational Study of Flow Interactions over a Close Coupled Canard-Wing on Fighter Setyawan Bekti Wibowo Universitas Gadjah Mada, Indonesia, [email protected] Sutrisno Sutrisno Universitas Gadjah Mada, [email protected] Tri Agung Rohmat Universitas Gadjah Mada, [email protected] Follow this and additional works at: https://commons.erau.edu/ijaaa Part of the Aerodynamics and Fluid Mechanics Commons, and the Computer-Aided Engineering and Design Commons Scholarly Commons Citation Wibowo, S. B., Sutrisno, S., & Rohmat, T. A. (2019). Computational Study of Flow Interactions over a Close Coupled Canard-Wing on Fighter. International Journal of Aviation, Aeronautics, and Aerospace, 6(1). https://doi.org/10.15394/ijaaa.2019.1306 This Article is brought to you for free and open access by the Journals at Scholarly Commons. It has been accepted for inclusion in International Journal of Aviation, Aeronautics, and Aerospace by an authorized administrator of Scholarly Commons. For more information, please contact [email protected]. Wibowo et al.: Flow Interactions over a Close Coupled Canard Introduction Aircraft technology is always evolving to improve efficiency and flight ability. One of the improvement efforts is by modifying the flow along the fuselage by adding a canard to the front of the aircraft wing. Canard is a part of an airplane that functions as a stabilizer or elevator and is placed in front of the main wing (Crane, 2012). The addition of a pair of canard wings will increase the lift force while delaying the occurrence of a stall at high angles.
    [Show full text]