Criteria for Conically-Scanned
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

H0 STET LER LQPCKET File Copy ORIGINAL
BAKER & H 0 S T E T LER LQPCKET FilE copy ORIGINAL COUNSELLORS AT LAW WASHINGTON SQUARE, SUITE 1100 • 1050 CONNECTICUT AVENUE, N.W. • WASHINGTON, D.C. 20036-5304 • (202) 861-1500 FAX (202) 861-1783 WRITER'S DIRECT DIAL NUMBER (202) 861-1624 December 17, 1997 VIA HAND DELIVERY Ms. Magalie Roman Salas Secretary Federal Communications Commission 1919 M Street, N.W. Room 222 Washington, D.C. 20554 Re: Advanced Television Systems and Their Impact upon the Existing Television Broadcast Service MM Docket No. 87-268 Comments Dear Ms .. Salas: We are transmitting herewith the original and five copies of the comments of Scripps Howard Broadcasting Company in the above captioned proceeding. The comments are filed pursuant to the Commission's Public Notice of December 2, 1997. Please contact the undersigned if you have any questions. Donald Enclosures (JJ-~ No. of Copies rec'd_. _ List ABCDE ORLANDO, FLORIDA CLEVELAND. OHIO COLUMBUS, OHIO DENVER. COLORADO HOUSTON. TEXAS LONG BEACH, CALIFORNIA Los ANGELES. CALIFORNIA (216) 621-0200 (614) 228-1541 (303) 861-0600 (713) 751-1600 (562) 432-2827 (213) 624-2400 (407) 649-4000 Before the DOCKET ALE CQPY ORlGlNAL FEDERAL COMMUNICATIONS COMMISSION Washington, D.C. 20554 In the matter of ) ) FCC SEEKS COMMENTS ON FILINGS ) ADDRESSING DIGITAL ) TV ALLOTMENTS, PUBLIC NOTICE ) dated December 2, 1997 ) TO: The Commission COMMENTS SUBMITTED BY SCRIPPS HOWARD BROADCASTING COMPANY These comments by Scripps Howard Broadcasting Company (SHBC) are in response to the PUBLIC NOTICE from the Federal Communications Commission (FCC) dated December 2, 1997 and signed by Richard M. Smith, Chief, Office ofEngineering and Technology. -

Experimental Results of Network-Assisted Interference Suppression Scheme Using Adaptive Beam-Tilt Switching
Hindawi International Journal of Antennas and Propagation Volume 2017, Article ID 2164038, 10 pages https://doi.org/10.1155/2017/2164038 Research Article Experimental Results of Network-Assisted Interference Suppression Scheme Using Adaptive Beam-Tilt Switching Tomoki Murakami,1 Riichi Kudo,1 Koichi Ishihara,1 Masato Mizoguchi,1 and Naoki Honma2 1 NTT Access Network Service Systems Laboratories, Nippon Telegraph and Telephone Corporation, Yokosuka, Japan 2Faculty of Engineering, Iwate University, Morioka, Japan Correspondence should be addressed to Tomoki Murakami; [email protected] Received 4 October 2016; Accepted 18 April 2017; Published 14 May 2017 Academic Editor: Ahmed Toaha Mobashsher Copyright © 2017 Tomoki Murakami et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. This paper introduces a network-assisted interference suppression scheme using beam-tilt switching per frame for wireless local area network systems and its effectiveness in an actual indoor environment. In the proposed scheme, two access points simultaneously transmit to their own desired station by adjusting angle of beam-tilt including transmit power assisted from network server for the improvement of system throughput. In the conventional researches, it is widely known that beam-tilt is effective for ICI suppression in the outdoor scenario. However, the indoor effectiveness of beam-tilt for ICI suppression has not yet been indicated from the experimental evaluation. Thus, this paper indicates the effectiveness of the proposed scheme by analyzing multiple-input multiple- output channel matrices from experimental measurements in an office environment. -

Uhf Slot Antenna
UHF SLOT ANTENNA PROSTAR SERIES Proven performance, quality and reliability Rugged construction Directional patterns standard & custom High power rating to achieve 5 megawatts Custom electrical & mechanical beam tilt Horizontal, circular & elliptical polarization ELECTRICAL SPECIFICATIONS Polarization Horizontal, Elliptical, Circular Power Rating 1 kW to 90 kW Beam Tilt As specified by customer Null Fill As specified by customer Input Impedance 50 or 75 ohm VSWR 1.1:1 or better across band 6340 Sky Creek Dr, Sacramento, CA 95828 | T: 916.383.1177 | F: 916.383.1182 JAMPRO.com UHF SLOT ANTENNA SELECTING YOUR SLOT ANTENNA Compatible with DTV, NTSC and PAL Broadcasts JA-LS: 1 kW JAMPRO’s LOW POWER slot antenna is designed with the needs of low power UHF broadcasters in mind. Aluminum construction ensures excellent weather resistance while residing windload and weight on the tower. The unique design of the low power UHF slot antenna can be configured to provide varying levels of vertically polarized signal. The versatility of the slots allows them to be top, leg or face mounted. JA-MS: 1 to 30 kW JAMPRO’s JA/MS is the harsh environment version of the JA/LS antenna. The JA/MS is also enclosed by white UV resistant radomes for added protection from the environment. The JA/MS is an excellent choice for low power UHF broadcasters located in areas with heavy air pollution or high salt content in the air. JSL-SERIES: 5 to 40 kW JAMPRO’s Premium LOW POWER slot antenna, using marine brass, copper and virgin Teflon in construc- tion, is the finest antenna of its type. -

R&D Report 1965-08
-- --------~ ---~------------'"-~~~~-----~ -----..:.-....-~---------"'--'---~--:~~---~-- RESEARCH DEPARTMENT SPECIFICATION OF THE IMPEDANCE OF TRANSMITTING AERIALS FOR MONOCHROME AND COLOUR TELEVISION SIGNALS Technological Report No. E-ll5 (1965/8) D.J. Why the , B.Sc.(Eng.), A.M.LE.E. for Head of Research Department --~-~ ------~:..~-~-~- ---- --------------- -- --------~-------- This Report Is the property ot the British Broadcasting Corporation and may not be reproduced in any form .ithout the written permission o~ the Corporation. - --". - - ~ ---------~------------- ~---~--.----------~~ -.:-'-. Technological Report No. E-115 SPECIFICATION OF mE IMPEDANCE OF TRANSMITTING AERIALS FOR MONOCHROME AND COLOUR TELEVISION SIGNALS Section Title Page SUMMARY ... 1 1. INTRODUCTION 1 2. 405-LINE MONOaIROME SYSTEM 2 2.1. Short-delay Reflexions. 2 2.2. Long-delay Reflexions . 2 3. 625-LINE MONOaIROME SYSTEM 3 3.1. Application of 405-line Results 3 3.2. Short-delay Reflexions 3 3.3. Long-delay Reflexions 4 4. 625-LINE COLOUR SYSTEM 4 4.1. General . 4 4.2. Short-delay Reflexions 5 4.3. Long-delay Reflexions 5 4.3.1. General 5 4.3.2. Subj ecti ve Tests 5 4.3.3. Results of Subjective Tests. 8 4.3.4. Resulting Specification 10 5. REFLEXIONS DUE TO FEEDER IRREGULARITIES 11 6. APPLICATION TO PRACTICAL INSTALLATIONS 12 6.1. The Aerial Impedance Specification . 12 6.1.1. The Effect of Loss in the Feeder and Combining Filters. 12 6.1.2. The Effect of Loss in Re-reflexion at the Transmitter. 12 C~~~~_~~_~ ________: ______ ~ ________ ~~~ ___ ~~ _______ ~ __ ~~ _______ ~ __ ~ _______ ~~ __ _ Section Title Page 6.2. Specification of Reflexions due to Feeder Irregulari ties,. 14 6.2.1. -

Antenna Design for Future Broadcast Technology
BROADCAST ANTENNA DESIGN TO SUPPORT FUTURE TRANSMISSION TECHNOLOGIES John L. Schadler Director of Antenna Development Dielectric L.L.C. Raymond, ME. Summary done by increasing the beam tilt at one site in order to reduce the amount of coverage area and thus the amount It doesn’t matter what future television transmission of traffic within that cell and avoid inter-cell interference technology is being discussed for the new ATSC3.0, they with neighboring cells. New groups of sites are then all have one thing in common, the need for higher data installed to fill in the gaps. The smaller cells allow for a rates and more channel capacity. Broadcasters will greater level of frequency re-use providing more channels become “Bit Managers” knowing that more power per unit coverage area. equates to higher quality of service (QoS). With broad industry consensus, assumptions can be made about next Although the method will be different, the idea of future generation systems. In general they will be based on proofing a high power broadcast antenna in anticipation orthogonal frequency division multiplexing (OFDM) of next generation broadcast requirements should be synchronous single frequency networks (SFN) limited considered. In any of the proposed next generation within the current coverage footprint as defined by the systems, the digital bandwidth is not limited by the FCC and will have the flexibility to support capacity number of users, but by the data rate supported within a growth. As a result of post-auction repack there is likely given carrier to noise ratio (C/N). Increasing the capacity to be more co-located channel sharing requiring is not done by reducing the traffic, but by increasing the broadband antenna systems with the central high power amount of throughput that can be delivered. -

Download PDF (476K)
IEICE Communications Express, Vol.6, No.6, 405–410 Performance enhancement by beam tilting in SD transmission utilizing two-ray fading Tomohiro Seki1a), Ken Hiraga2, Kazumitsu Sakamoto2, and Maki Arai2 1 College of Industrial Technology, Department of Electrical and Electronic Engineering, Nihon University, 1–2–1 Izumicho, Narashino 275–8575, Japan 2 NTT Network Innovation Laboratories, NTT Corporation, 1–1 Hikarinooka, Yokosuka 239–0847, Japan a) [email protected] Abstract: A method is proposed for enhancing the transmission perform- ance in a spatial division transmission system that utilizes the fading characteristics of two-ray ground reflection propagation. The method is tilting the elevation angle of antenna beams purposely towards out of the communicating peer. Using ray-tracing simulation, it is shown that the performance of the system is significantly improved when high-gain anten- nas with narrow beamwidth are used. Keywords: two-ray fading, parallel transmission Classification: Antennas and Propagation References [1] K. Hiraga, K. Sakamoto, M. Arai, T. Seki, T. Nakagawa, and K. Uehara, “Spatial division transmission without signal processing for MIMO detection utilizing two-ray fading,” IEICE Trans. Commun., vol. E97.B, no. 11, pp. 2491–2501, 2014. DOI:10.1587/transcom.E97.B.2491 [2] C. Cordeiro, “IEEE doc.:802.11-09/1153r2,” p. 4, 2009. [3] Wilocity: Wil6200 Chipset Datasheet. [Online]. http://wilocity.com/resources/ Wil6200-Brief.pdf. [4] W. L. Stutzman, “Estimating directivity and gain of antennas,” IEEE Antennas Propag. Mag., vol. 40, no. 4, pp. 7–11, Aug. 1998. DOI:10.1109/74.730532 [5] D. Parsons, The Mobile Radio Propagation Channel, ch. -

Dielectric • 22 Tower Rd., Raymond, ME 04071 USA • +1 207-655-8100
DIE 18331 - TV Planner:9998_DTV Brochure_2003 12/21/16 12:44 PM Page 1 Dielectric • 22 Tower Rd., Raymond, ME 04071 USA • +1 207-655-8100 • www.dielectric.com • TVPlanner07/2013 1 DIE18331 TV Planner_12-30-2013:9998_DTV Brochure_2003 12/30/13 12:14 PM Page 1 Dielectric Communications: Advancing Full System Solutions the frontier Since our inception in 1942, we have considered ourselves a solutions oriented engineering company, priding ourselves on our depth of scientific in broadcast experience and knowledge. Clients approach us with broadcast needs and we communications deliver full system solutions, jointly tasking with client engineering staff design technologically advanced systems. We design and manufacture full broadcast for over seven systems from the transmitter output to the tower top. decades. A Culture of innovation spanning over seven decades. Dielectric’s leadership in passive RF technologies is reflected in the expertise we offer and the recognition we’ve received: over 100 patents, 2 emmys for technical innovation, 4 NAB Pick hits, to name a few. Dielectric offers the customized support services and planning tools you need to build your television antenna from configuring a new antenna system, to acquiring knowledgeable insights into specific technical issues, Dielectric resources provide easy access to the assistance you needed. This includes customized support services, as well as planning tools to guide in the design. Call Us This fifth edition of our television planning guide details the systems and components we produce. Call us about your requirements or any of our broad- cast products at 1-800-341-9678. Products contained in this catalog may be covered by one or more of the following patents: 6,917,264; 6,903,624; 6,887,093; 6,882,224; 6,870,443; 6,867,743; 6,816,040; 6,703,984; 6,703,911; 6,677,916; 6,650,300; 6,650,209; 6,617,940; 6,538,529; 6,373,444; 6,320,555; 5,999,145; 5,861,858; 5,455,548; 5,418,545; 5,401,173; 5,167,510; 4,988,961; 4,951,013; 4,899,165; 4,723,307; 4,654,962; 4,602,227. -
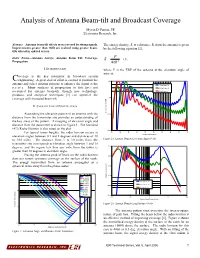
Analysis of Antenna Beam-Tilt and Broadcast Coverage
Analysis of Antenna Beam-tilt and Broadcast Coverage Myron D. Fanton, PE Electronics Research, Inc. Abstract—Antenna beam tilt affects areas covered by strong signals. The energy density, S, at a distance, R, from the antenna is given Improvements greater than 10dB are realized using greater beam- by the following equation [2], tilts offered in end-fed arrays. P Index Terms—Antenna Arrays, Antenna Beam Tilt, Coverage, S = (1), Propagation 4πR 2 I. INTRODUCTION where P is the ERP of the antenna at the elevation angle of interest. overage is the key parameter in broadcast system engineering. A great deal of effort is exerted to position the C 0.00 antenna and select antenna patterns to enhance the signal at the 1.5 Deg. Beam Tilt receiver. Many analyses of propagation to date have not 0.5 Deg. Beam Tilt accounted for antenna beam-tilt, though now technology, 0 Deg. Beam Tilt products, and analytical techniques [1] can optimize the coverage with increased beam-tilt. -5.00 II. SMOOTH EARTH PROPAGATION Amplitude on Ground (dB) Associating the elevation pattern of an antenna with the -10.00 distance from the transmitter site provides an understanding of the key areas of the pattern. A mapping of elevation angle and distance from the transmitter is shown in Figure 1. The Standard (4/3) Radio Horizon is also noted on the plot. -15.00 For typical tower heights, the radio horizon occurs at 90 80 70 60 50 40 30 20 10 0 Elevation Angle (Degrees) elevation angles between 0.1 and 1 degrees and distances of 10 to 100 miles. -

Antennas - Catalogue 19
ANTENNAS - CATALOGUE 19 KATHREIN Broadcast GmbH Ing.-Anton-Kathrein-Str. 1–7 83101 Rohrdorf, Germany www.kathrein-bca.com [email protected] TOTAL QUALITY MANAGEMENT INDEX FM Antennas 3 VHF Antennas 39 UHF Antennas 63 Technical Notes 81 1 FM ANTENNAS INDEX FM-03 H 5 FM-03 V 9 FM-04 13 FM-05 H 15 FM-07 19 FM-34 21 FMC-01 22 FMC-01/R 24 FMC-03 26 FMC-05 30 FMC-06 34 FMC-06/R 36 FM ANTENNAS 3 FM-03 (Horizontal polarization) FM PANEL ANTENNA FEATURES • horizontal polarization • broadband 87.5 ÷ 108 MHz • 7.5 dB gain • directional pattern • suitable as a component in various arrays on square towers • stainless steel dipoles • suitable also for vertical polarization RADIATION PATTERNS (Mid Band) ELECTRICAL DATA ANTENNA TYPE FM-03 FREQUENCY RANGE 87.5 ÷ 108 MHz IMPEDANCE 50 ohm CONNECTOR 7/8” EIA MAX POWER 5 kW VSWR ≤ 1.15 POLARIZATION Horizontal GAIN (referred to half wave dipole) 7.5 dB E-Plane ± 34° HALF POWER BEAMWIDTH H-Plane ± 30° LIGHTNING PROTECTION All Metal Parts DC Grounded MECHANICAL DATA 2200 x 2000 x 991 DIMENSIONS mm (in) (86.61 x 78.74 x 39.02) WEIGHT kg (lb) 61 (134.5) 1.40 (15.1) front WIND SURFACE m2 ( ft2) 1.01 (10.9) side WIND LOAD kN (lbf) 1.76 (396) front at 160 km/h (100 mph) 1.25 (281) side MAX WIND VELOCITY km/h (mph) 270 (167.8) Reflector (hot dip galvanized steel) Dipoles (stainless steel) MATERIALS Internal parts (silver plated brass, polished brass, deoxidized aluminium) Radome (fiberglass) ICING PROTECTION Feed point radome RADOME COLOUR Grey (standard) MOUNTING Directly on supporting mast Specifications are subject to change without prior notice FM ANTENNAS 5 FM-03 (Horizontal polarization) FM PANEL ANTENNA FEATURES • radiating systems with FM-03 panel • high power systems • omnidirectional or directional patterns • equal or unequal split ratio power distribution network FM-03/32 (8x4) GUANGZHOU, P.R.C. -

Advanced Antenna Technology
1/135 TABLE OF CONTENTS 1. BACKGROUND AND SCOPE OF WHITEPAPER ........................................................................................... 14 2. BASE STATION ANTENNA EVOLUTION ........................................................................................................ 19 2.1. EARLY TECHNOLOGY ........................................................................................................................................... 19 2.2. CURRENT TECHNOLOGY ....................................................................................................................................... 20 2.2.1. Extensive Usage ................................................................................................................................. 20 2.2.2. Moderate Usage ................................................................................................................................. 21 2.2.3. Advanced Antenna Technology .......................................................................................................... 22 2.2.4. MIMO Systems ................................................................................................................................... 23 2.2.5. Reconfigurable Beam Antenna ........................................................................................................... 24 2.2.6. Active Antenna .................................................................................................................................... 25 2.3. COMPARISON TABLE—ANTENNA -

A Twelve-Beam Steering Low Profile Patch Antenna with Shorting Vias for Vehicular Applications
View metadata, citation and similar papers at core.ac.uk brought to you by CORE IEEE Transactions on Antennas and Propgataion: Final checks and corrections are being performed provided by University of Essex Research Repository A Twelve-Beam Steering Low Profile Patch Antenna with Shorting Vias for Vehicular Applications Arpan Pal, Member, IEEE, Amit Mehta, Senior Member, IEEE, Dariush Mirshekar-Syahkal, Fellow, IEEE, Hisamatsu Nakano, Life Fellow, IEEE inevitable losses) and complex signal processing for their operation. Therefore, they are not suitable for low price modern Abstract—A low-profile twelve-beam printed patch antenna is commercial portable wireless transceivers. presented for pattern reconfigurable applications. The patch is As an alternative, single element Beam Steering Antennas fed at the four sides using coaxial feeds. Diagonal lines of vias are (BSAs) [5]-[21] have been proposed recently for manoeuvring inserted on the patch surface to restrict currents to the edges. Whilst majority of patch antennas have an axial beam pattern, the antenna radiation beam in space. Being single element, these proposed antenna produces twelve different tilted beams. When antennas are small, lightweight, require small signal processing one of its four feeds on the sides is excited and the remaining feeds and either need no or diminutive phase shifters. The rectangular are open circuited, the antenna generates a linearly polarized spiral antenna [5]-[8] was the initial one in this class. To steer tilted beam (6.2 dBi, θmax = 30°). This beam is directed away from its beam, the current distribution over the spiral arm is varied feeding patch corner. Therefore, the antenna can steer its tilted using switches, but the antenna has limited beam steering beam in four different space quadrants in front of the antenna by exciting one feed at a time. -

Druckschrift 99811574, Professional Broadcast Antennas
Glossary of Broadcast Antenna Terms Antenna Gain The cross section of the mast or tower should be less than one wavelength for a good omni pattern. The gain of an array describes the increase As the cross section increases beyond one of signal in the main radiation direction which wavelength nulls in the horizontal radiation pattern is produced by reducing radiation in all other will rapidly become deeper. directions and concentrating it in the main beam. The gain of a broadcast antenna system is Measurement Links normally increased by using a larger number of vertical bays (increasing the vertical aperture) and When large-diameter coax lines are used in an thereby forming a more narrow vertical radiation antenna system it is not possible to easily connect pattern. measurement equipment without dis assembly of In the case of a directional antenna system the the coax system. In these cases it is advisable to gain is increased by reducing or eliminating install measurement links in the coax feeders to radiation toward azimuth segments and re- allow convenient connection of test equipment to directing it toward the areas where coverage is the antenna system. desired. Mismatch Compensation When calculating the gain of an array the losses in the feeder cables and the power splitters must be In a broadcast panel array the impedance match taken into account. of individual panels can be disturbed by mutual coupling, icing and the presence of nearby Downtilt in Panel Arrays obstacles. For this reason it is necessary to design the feed system so as to cancel reflections within When transmitting antennas are located on ele- the array and thereby minimize the presence of vated sites it is often beneficial to tilt the main reflected signal at the antenna system input.