Chapter 2. New Worlds Versus Scaling: from Van Leeuwenhoek to Mandelbrot
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Using Concrete Scales: a Practical Framework for Effective Visual Depiction of Complex Measures Fanny Chevalier, Romain Vuillemot, Guia Gali
Using Concrete Scales: A Practical Framework for Effective Visual Depiction of Complex Measures Fanny Chevalier, Romain Vuillemot, Guia Gali To cite this version: Fanny Chevalier, Romain Vuillemot, Guia Gali. Using Concrete Scales: A Practical Framework for Effective Visual Depiction of Complex Measures. IEEE Transactions on Visualization and Computer Graphics, Institute of Electrical and Electronics Engineers, 2013, 19 (12), pp.2426-2435. 10.1109/TVCG.2013.210. hal-00851733v1 HAL Id: hal-00851733 https://hal.inria.fr/hal-00851733v1 Submitted on 8 Jan 2014 (v1), last revised 8 Jan 2014 (v2) HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Using Concrete Scales: A Practical Framework for Effective Visual Depiction of Complex Measures Fanny Chevalier, Romain Vuillemot, and Guia Gali a b c Fig. 1. Illustrates popular representations of complex measures: (a) US Debt (Oto Godfrey, Demonocracy.info, 2011) explains the gravity of a 115 trillion dollar debt by progressively stacking 100 dollar bills next to familiar objects like an average-sized human, sports fields, or iconic New York city buildings [15] (b) Sugar stacks (adapted from SugarStacks.com) compares caloric counts contained in various foods and drinks using sugar cubes [32] and (c) How much water is on Earth? (Jack Cook, Woods Hole Oceanographic Institution and Howard Perlman, USGS, 2010) shows the volume of oceans and rivers as spheres whose sizes can be compared to that of Earth [38]. -

Charles and Ray Eames's Powers of Ten As Memento Mori
chapter 2 Charles and Ray Eames’s Powers of Ten as Memento Mori In a pantheon of potential documentaries to discuss as memento mori, Powers of Ten (1968/1977) stands out as one of the most prominent among them. As one of the definitive works of Charles and Ray Eames’s many successes, Pow- ers reveals the Eameses as masterful designers of experiences that communi- cate compelling ideas. Perhaps unexpectedly even for many familiar with their work, one of those ideas has to do with memento mori. The film Powers of Ten: A Film Dealing with the Relative Size of Things in the Universe and the Effect of Adding Another Zero (1977) is a revised and up- dated version of an earlier film, Rough Sketch of a Proposed Film Dealing with the Powers of Ten and the Relative Size of Things in the Universe (1968). Both were made in the United States, produced by the Eames Office, and are widely available on dvd as Volume 1: Powers of Ten through the collection entitled The Films of Charles & Ray Eames, which includes several volumes and many short films and also online through the Eames Office and on YouTube (http://www . eamesoffice.com/ the-work/powers-of-ten/ accessed 27 May 2016). The 1977 version of Powers is in color and runs about nine minutes and is the primary focus for the discussion that follows.1 Ralph Caplan (1976) writes that “[Powers of Ten] is an ‘idea film’ in which the idea is so compellingly objectified as to be palpably understood in some way by almost everyone” (36). -

Urantia, a Cosmic View of the Architecture of the Universe
Pr:rt llr "Lost & First Men" vo-L-f,,,tE 2 \c 2 c6510 ADt t 4977 s1 50 Bryce Bond ot the Etherius Soeie& HowTo: ond, would vou Those Stronge believe. Animol Mutilotions: Aicin Wotts; The Urontic BookReveols: N Volume 2, Number 2 FRONTIERS April,1977 CONTENTS REGULAR FEATURES_ Editorial .............. o Transmissions .........7 Saucer Waves .........17 Astronomy Lesson ...... ........22 Audio-Visual Scanners ...... ..7g Cosmic Print-Outs . ... .. ... .... .Bz COSMIC SPOTLIGHTS- They Came From Sirjus . .. .....Marc Vito g Jack, The Animal Mutilator ........Steve Erdmann 11 The Urantia Book: Architecture of the Universe 26 rnterview wirh Alan watts...,f ro, th" otf;lszidThow ut on the Frontrers of science; rr"u" n"trno?'rnoLllffill sutherly 55 Kirrian photography of the Human Auracurt James R. Wolfe 58 UFOs and Time Travel: Doing the Cosmic Wobble John Green 62 CF SERIAL_ "Last & paft2 First Men ," . Olaf Stapledon 35 Cosmic Fronliers;;;;;;J rs DUblrshed Editor: Arthur catti bi-morrhiyy !y_g_oynby Cosm i publica- Art Director: Vincent priore I ons, lnc. at 521 Frith Av.nr."Jb.ica- | New York,i:'^[1 New ';;'].^iffiiYork 10017. I Associate Art Director: Fiank DeMarco Copyright @ 1976 by Cosmic Contributing Editors:John P!blications.l-9,1?to^ lnc, Alt ?I,^c-::Tf riohrs re- I creen, Connie serued, rncludrnqiii,jii"; i'"''1,1.",th€ irqlil ot lvlacNamee. Charles Lane, Wm. Lansinq Brown. jon T; I reproduction ,1wr-or€rn whol€ o,or Lnn oarrpa.'. tsasho Katz, A. A. Zachow, Joseph Belv-edere SLngle copy price: 91.50 I lnside Covers: Rico Fonseca THE URANTIA BOOK: lhe Cosmic view of lhe ARCHITECTURE of lhe UNIVERSE -qnd How Your Spirit Evolves byA.A Zochow Whg uos monkind creoted? The Isle of Paradise is a riers, the Creaior Sons and Does each oJ us houe o pur. -

Detection of PAH and Far-Infrared Emission from the Cosmic Eye
Accepted for publication in ApJ A Preprint typeset using LTEX style emulateapj v. 08/22/09 DETECTION OF PAH AND FAR-INFRARED EMISSION FROM THE COSMIC EYE: PROBING THE DUST AND STAR FORMATION OF LYMAN BREAK GALAXIES B. Siana1, Ian Smail2, A. M. Swinbank2, J. Richard2, H. I. Teplitz3, K. E. K. Coppin2, R. S. Ellis1, D. P. Stark4, J.-P. Kneib5, A. C. Edge2 Accepted for publication in ApJ ABSTRACT ∗ We report the results of a Spitzer infrared study of the Cosmic Eye, a strongly lensed, LUV Lyman Break Galaxy (LBG) at z =3.074. We obtained Spitzer IRS spectroscopy as well as MIPS 24 and 70 µm photometry. The Eye is detected with high significance at both 24 and 70 µm and, when including +4.7 11 a flux limit at 3.5 mm, we estimate an infrared luminosity of LIR = 8.3−4.4 × 10 L⊙ assuming a magnification of 28±3. This LIR is eight times lower than that predicted from the rest-frame UV properties assuming a Calzetti reddening law. This has also been observed in other young LBGs, and indicates that the dust reddening law may be steeper in these galaxies. The mid-IR spectrum shows strong PAH emission at 6.2 and 7.7 µm, with equivalent widths near the maximum values observed in star-forming galaxies at any redshift. The LP AH -to-LIR ratio lies close to the relation measured in local starbursts. Therefore, LP AH or LMIR may be used to estimate LIR and thus, star formation rate, of LBGs, whose fluxes at longer wavelengths are typically below current confusion limits. -

Close-Up View of a Luminous Star-Forming Galaxy at Z = 2.95 S
Close-up view of a luminous star-forming galaxy at z = 2.95 S. Berta, A. J. Young, P. Cox, R. Neri, B. M. Jones, A. J. Baker, A. Omont, L. Dunne, A. Carnero Rosell, L. Marchetti, et al. To cite this version: S. Berta, A. J. Young, P. Cox, R. Neri, B. M. Jones, et al.. Close-up view of a luminous star- forming galaxy at z = 2.95. Astronomy and Astrophysics - A&A, EDP Sciences, 2021, 646, pp.A122. 10.1051/0004-6361/202039743. hal-03147428 HAL Id: hal-03147428 https://hal.archives-ouvertes.fr/hal-03147428 Submitted on 19 Feb 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. A&A 646, A122 (2021) Astronomy https://doi.org/10.1051/0004-6361/202039743 & c S. Berta et al. 2021 Astrophysics Close-up view of a luminous star-forming galaxy at z = 2.95? S. Berta1, A. J. Young2, P. Cox3, R. Neri1, B. M. Jones4, A. J. Baker2, A. Omont3, L. Dunne5, A. Carnero Rosell6,7, L. Marchetti8,9,10 , M. Negrello5, C. Yang11, D. A. Riechers12,13, H. Dannerbauer6,7, I. -

A Biblical View of the Cosmos the Earth Is Stationary
A BIBLICAL VIEW OF THE COSMOS THE EARTH IS STATIONARY Dr Willie Marais Click here to get your free novaPDF Lite registration key 2 A BIBLICAL VIEW OF THE COSMOS THE EARTH IS STATIONARY Publisher: Deon Roelofse Postnet Suite 132 Private Bag x504 Sinoville, 0129 E-mail: [email protected] Tel: 012-548-6639 First Print: March 2010 ISBN NR: 978-1-920290-55-9 All rights reserved. No part of this publication may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopy, recording or any information storage and retrieval system, without permission in writing from the publisher. Cover design: Anneette Genis Editing: Deon & Sonja Roelofse Printing and binding by: Groep 7 Printers and Publishers CK [email protected] Click here to get your free novaPDF Lite registration key 3 A BIBLICAL VIEW OF THE COSMOS CONTENTS Acknowledgements...................................................5 Introduction ............................................................6 Recommendations..................................................14 1. The creation of heaven and earth........................17 2. Is Genesis 2 a second telling of creation? ............25 3. The length of the days of creation .......................27 4. The cause of the seasons on earth ......................32 5. The reason for the creation of heaven and earth ..34 6. Are there other solar systems?............................36 7. The shape of the earth........................................37 8. The pillars of the earth .......................................40 9. The sovereignty of the heaven over the earth .......42 10. The long day of Joshua.....................................50 11. The size of the cosmos......................................55 12. The age of the earth and of man........................59 13. Is the cosmic view of the bible correct?..............61 14. -

(1) a Directory to Sources Of
DOCUMENT' RESUME ED 027 211 SE006 281 By-McIntyre, Kenneth M. Space ScienCe Educational Media Resources, A Guide for Junior High SchoolTeachers. NatiOnal Aeronautics and Space Administration, Washington, D.C. Pub Date Jun 66 Note-108p. Available from-National Aeronautics and Space Administration, Washington, D.C.($3.50) EDRS Price MF -$0.50 HC Not Available from EDRS. Descriptors-*Aerospace Technology, Earth Science, Films, Filmstrips, Grade 8,*Instructional Media, *Resource Guides, *Science Activities, *Secondary School Science, Teaching Guides,Transparencies Identifiers-National Aeronautics and Space AdMinistration This guide, developed bya panel of teacher consultants, is a correlation of educational mediaresources with the "North Carolina Curricular Bulletin for Eighth Grade Earth and Space Science" and thestate adopted textbook, pModern Earth Science." The three maior divisionsare (1) the Earth in Space (Astronomy), (2) Space Exploration, and (3) Meterology. Included. for theprimary topics under each division are (1) statements of concepts, (2) student activities, and (3) annotated listings of films, filmstrips, film-loops, transparencies, slides,and other forms of instructional media. Appendixesare (1) a directory to sources of instructional media, (2) a title index to the films and filmstrips cited, (3)a listing of bibliographies, guides, and printed materials related to aerospace edUcation. (RS) DOCUMENT. RESUM.E. ED 027 211 SE 006 281 By-McIntyre, Kenneth M. Space ScienCe Educational Media Resources, A Guide for JuniorHigh School Teachers. National Aeronautics and Space Administration, Washington, D.C. Pub Date Jun 66 Note-108p. Available from-National Aeronautics and Space Administration, Washington, D.C.($3.50) EDRS Price MF -$0.50 HC Not Available from EDRS. -

Ast110fall2015-Labmanual.Pdf
2015/2016 (http://astronomy.nmsu.edu/astro/Ast110Fall2015.pdf) 1 2 Contents 1IntroductiontotheAstronomy110Labs 5 2TheOriginoftheSeasons 21 3TheSurfaceoftheMoon 41 4ShapingSurfacesintheSolarSystem:TheImpactsofCometsand Asteroids 55 5IntroductiontotheGeologyoftheTerrestrialPlanets 69 6Kepler’sLawsandGravitation 87 7TheOrbitofMercury 107 8MeasuringDistancesUsingParallax 121 9Optics 135 10 The Power of Light: Understanding Spectroscopy 151 11 Our Sun 169 12 The Hertzsprung-Russell Diagram 187 3 13 Mapping the Galaxy 203 14 Galaxy Morphology 219 15 How Many Galaxies Are There in the Universe? 241 16 Hubble’s Law: Finding the Age of the Universe 255 17 World-Wide Web (Extra-credit/Make-up) Exercise 269 AFundamentalQuantities 271 BAccuracyandSignificantDigits 273 CUnitConversions 274 DUncertaintiesandErrors 276 4 Name: Lab 1 Introduction to the Astronomy 110 Labs 1.1 Introduction Astronomy is a physical science. Just like biology, chemistry, geology, and physics, as- tronomers collect data, analyze that data, attempt to understand the object/subject they are looking at, and submit their results for publication. Along thewayas- tronomers use all of the mathematical techniques and physics necessary to understand the objects they examine. Thus, just like any other science, a largenumberofmath- ematical tools and concepts are needed to perform astronomical research. In today’s introductory lab, you will review and learn some of the most basic concepts neces- sary to enable you to successfully complete the various laboratory exercises you will encounter later this semester. When needed, the weekly laboratory exercise you are performing will refer back to the examples in this introduction—so keep the worked examples you will do today with you at all times during the semester to use as a refer- ence when you run into these exercises later this semester (in fact, on some occasions your TA might have you redo one of the sections of this lab for review purposes). -

Trillion Theory: a New Cosmic Theory
European J of Physics Education Volume 11 Issue 4 1309-7202 Lukowich Trillion Theory: A New Cosmic Theory Ed Lukowich Cosmology Theorist from Calgary, Alberta, Canada Graduated from University of Saskatchewan, Saskatoon, Saskatchewan, Canada [email protected] (Received 08.09.2019, Accepted 22.09.2019) INTRODUCTION Trillion Theory (TT), a new theory, estimates the cosmic origin at one trillion years. This calculation of thousands of eons is based upon a growth factor where solar systems age-out at a max of 15 billion years, only to recycle into even larger solar systems, inside of ancient galaxies that are as old as 200 billion to 900 billion years. TT finds a Black Hole inside of each sphere (planet, moon, sun). Black Holes built and recycled solar systems inside humongous galaxies over a trillion cosmic years. 5 possible future proofs for Trillion Theory. - Proof 1: Finding a Black Hole inside of a sphere. Cloaked Black Hole gives sphere axial spin and gravity. - Proof 2: Black Hole survives Supernova of its Sun. Discovery shows resultant Black Hole after a Supernova was always inside of its exploding Sun. - Proof 3: Discovery of a Black Hole graveyard. Where the Black Holes that occupied the spheres of a solar system are found naked, fighting for new light, after the Sun’s Supernova destroyed their system. - Proof 4: Discover that Supermassive Black Holes, at galaxy hubs, have evolved to be hundreds of billions of years old. - Proof 5: Emulate, inside of a laboratory, the actions of a Black Hole spinning light into matter. This discovery shows how Black Holes capture and spin light to build spheres. -

12 Strong Gravitational Lenses
12 Strong Gravitational Lenses Phil Marshall, MaruˇsaBradaˇc,George Chartas, Gregory Dobler, Ard´ısEl´ıasd´ottir,´ Emilio Falco, Chris Fassnacht, James Jee, Charles Keeton, Masamune Oguri, Anthony Tyson LSST will contain more strong gravitational lensing events than any other survey preceding it, and will monitor them all at a cadence of a few days to a few weeks. Concurrent space-based optical or perhaps ground-based surveys may provide higher resolution imaging: the biggest advances in strong lensing science made with LSST will be in those areas that benefit most from the large volume and the high accuracy, multi-filter time series. In this chapter we propose an array of science projects that fit this bill. We first provide a brief introduction to the basic physics of gravitational lensing, focusing on the formation of multiple images: the strong lensing regime. Further description of lensing phenomena will be provided as they arise throughout the chapter. We then make some predictions for the properties of samples of lenses of various kinds we can expect to discover with LSST: their numbers and distributions in redshift, image separation, and so on. This is important, since the principal step forward provided by LSST will be one of lens sample size, and the extent to which new lensing science projects will be enabled depends very much on the samples generated. From § 12.3 onwards we introduce the proposed LSST science projects. This is by no means an exhaustive list, but should serve as a good starting point for investigators looking to exploit the strong lensing phenomenon with LSST. -
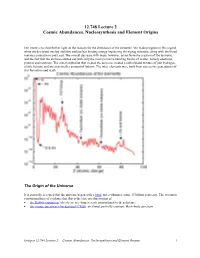
12.748 Lecture 2 Cosmic Abundances, Nucleosynthesis and Element Origins
12.748 Lecture 2 Cosmic Abundances, Nucleosynthesis and Element Origins Our intent is to shed further light on the reasons for the abundance of the elements. We made progress in this regard when we discussed nuclear stability and nuclear binding energy explaining the zigzag structure, along with the broad maxima around Iron and Lead. The overall decrease with mass, however, arises from the creation of the universe, and the fact that the universe started out with only the most primitive building blocks of matter, namely electrons, protons and neutrons. The initial explosion that created the universe created a rather bland mixture of just hydrogen, a little helium, and an even smaller amount of lithium. The other elements were built from successive generations of star formation and death. The Origin of the Universe It is generally accepted that the universe began with a bang, not a whimper, some 15 billion years ago. The two most convincing lines of evidence that this is the case are observation of • the Hubble expansion: objects are receding at a rate proportional to their distance • the cosmic microwave background (CMB): an almost perfectly isotropic black-body spectrum Isotopes 12.748 Lecture 2: Cosmic Abundances, Nucleosynthesis and Element Origins 1 In the initial fraction of a second, the temperature is so hot that even subatomic particles like neutrons, electrons and protons fall apart into their constituent pieces (quarks and gluons). These temperatures are well beyond anything achievable in the universe since. As the fireball expands, the temperature drops, and progressively higher-level particles are manufactured. By the end of the first second, the temperature has dropped to a mere billion degrees or so, and things are starting to get a little more normal: electrons, neutrons and protons can now exist. -

ASTR110G Astronomy Laboratory Exercises C the GEAS Project 2020
ASTR110G Astronomy Laboratory Exercises c The GEAS Project 2020 ASTR110G Laboratory Exercises Lab 1: Fundamentals of Measurement and Error Analysis ...... ....................... 1 Lab 2: Observing the Sky ............................... ............................. 35 Lab 3: Cratering and the Lunar Surface ................... ........................... 73 Lab 4: Cratering and the Martian Surface ................. ........................... 97 Lab 5: Parallax Measurements and Determining Distances ... ....................... 129 Lab 6: The Hertzsprung-Russell Diagram and Stellar Evolution ..................... 157 Lab 7: Hubble’s Law and the Cosmic Distance Scale ........... ..................... 185 Lab 8: Properties of Galaxies .......................... ............................. 213 Appendix I: Definitions for Keywords ..................... .......................... 249 Appendix II: Supplies ................................. .............................. 263 Lab 1 Fundamentals of Measurement and Error Analysis 1.1 Introduction This laboratory exercise will serve as an introduction to all of the laboratory exercises for this course. We will explore proper techniques for obtaining and analyzing data, and practice plotting and analyzing data. We will discuss a scientific methodology for conducting exper- iments in which we formulate a question, predict the behavior of the system based on likely solutions, acquire relevant data, and then compare our predictions with the observations. You will have a chance to plan a short experiment,