Plurality Voting Under Uncertainty
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

THE SINGLE-MEMBER PLURALITY and MIXED-MEMBER PROPORTIONAL ELECTORAL SYSTEMS : Different Concepts of an Election
THE SINGLE-MEMBER PLURALITY AND MIXED-MEMBER PROPORTIONAL ELECTORAL SYSTEMS : Different Concepts of an Election by James C. Anderson A thesis presented to the University of Waterloo in fulfillment of the thesis requirement for the degree of Master of Arts in Political Science Waterloo, Ontario, Canada, 2006 © James C. Anderson 2006 Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. Library and Bibliotheque et Archives Canada Archives Canada Published Heritage Direction du Branch Patrimoine de I'edition 395 Wellington Street 395, rue Wellington Ottawa ON K1A 0N4 Ottawa ON K1A 0N4 Canada Canada Your file Votre reference ISBN: 978-0-494-23700-7 Our file Notre reference ISBN: 978-0-494-23700-7 NOTICE: AVIS: The author has granted a non L'auteur a accorde une licence non exclusive exclusive license allowing Library permettant a la Bibliotheque et Archives and Archives Canada to reproduce,Canada de reproduire, publier, archiver, publish, archive, preserve, conserve,sauvegarder, conserver, transmettre au public communicate to the public by par telecommunication ou par I'lnternet, preter, telecommunication or on the Internet,distribuer et vendre des theses partout dans loan, distribute and sell theses le monde, a des fins commerciales ou autres, worldwide, for commercial or non sur support microforme, papier, electronique commercial purposes, in microform,et/ou autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriete du droit d'auteur ownership and moral rights in et des droits moraux qui protege cette these. this thesis. Neither the thesis Ni la these ni des extraits substantiels de nor substantial extracts from it celle-ci ne doivent etre imprimes ou autrement may be printed or otherwise reproduits sans son autorisation. -

Responsiveness, Capture and Efficient Policymaking
CENTRO DE INVESTIGACIÓN Y DOCENCIA ECONÓMICAS, A.C. ELECTIONS AND LOTTERIES: RESPONSIVENESS, CAPTURE AND EFFICIENT POLICYMAKING TESINA QUE PARA OBTENER EL GRADO DE MAESTRO EN CIENCIA POLÍTICA PRESENTA JORGE OLMOS CAMARILLO DIRECTOR DE LA TESINA: DR. CLAUDIO LÓPEZ-GUERRA CIUDAD DE MÉXICO SEPTIEMBRE, 2018 CONTENTS I. Introduction .............................................................................................................. 1 II. Literature Review ..................................................................................................... 6 1. Political Ambition .............................................................................................. 6 2. Electoral Systems and Policymaking ................................................................. 7 3. The Revival of Democracy by Lot ..................................................................... 8 III. Lottocracy in Theory .............................................................................................. 12 IV. Elections and Lotteries ........................................................................................... 14 1. Responsiveness ................................................................................................. 14 2. Legislative Capture ........................................................................................... 16 3. Efficiency.......................................................................................................... 18 V. A Formal Model of Legislator’s Incentives .......................................................... -

Are Condorcet and Minimax Voting Systems the Best?1
1 Are Condorcet and Minimax Voting Systems the Best?1 Richard B. Darlington Cornell University Abstract For decades, the minimax voting system was well known to experts on voting systems, but was not widely considered to be one of the best systems. But in recent years, two important experts, Nicolaus Tideman and Andrew Myers, have both recognized minimax as one of the best systems. I agree with that. This paper presents my own reasons for preferring minimax. The paper explicitly discusses about 20 systems. Comments invited. [email protected] Copyright Richard B. Darlington May be distributed free for non-commercial purposes Keywords Voting system Condorcet Minimax 1. Many thanks to Nicolaus Tideman, Andrew Myers, Sharon Weinberg, Eduardo Marchena, my wife Betsy Darlington, and my daughter Lois Darlington, all of whom contributed many valuable suggestions. 2 Table of Contents 1. Introduction and summary 3 2. The variety of voting systems 4 3. Some electoral criteria violated by minimax’s competitors 6 Monotonicity 7 Strategic voting 7 Completeness 7 Simplicity 8 Ease of voting 8 Resistance to vote-splitting and spoiling 8 Straddling 8 Condorcet consistency (CC) 8 4. Dismissing eight criteria violated by minimax 9 4.1 The absolute loser, Condorcet loser, and preference inversion criteria 9 4.2 Three anti-manipulation criteria 10 4.3 SCC/IIA 11 4.4 Multiple districts 12 5. Simulation studies on voting systems 13 5.1. Why our computer simulations use spatial models of voter behavior 13 5.2 Four computer simulations 15 5.2.1 Features and purposes of the studies 15 5.2.2 Further description of the studies 16 5.2.3 Results and discussion 18 6. -

On the Distortion of Voting with Multiple Representative Candidates∗
The Thirty-Second AAAI Conference on Artificial Intelligence (AAAI-18) On the Distortion of Voting with Multiple Representative Candidates∗ Yu Cheng Shaddin Dughmi David Kempe Duke University University of Southern California University of Southern California Abstract voters and the chosen candidate in a suitable metric space (Anshelevich 2016; Anshelevich, Bhardwaj, and Postl 2015; We study positional voting rules when candidates and voters Anshelevich and Postl 2016; Goel, Krishnaswamy, and Mu- are embedded in a common metric space, and cardinal pref- erences are naturally given by distances in the metric space. nagala 2017). The underlying assumption is that the closer In a positional voting rule, each candidate receives a score a candidate is to a voter, the more similar their positions on from each ballot based on the ballot’s rank order; the candi- key questions are. Because proximity implies that the voter date with the highest total score wins the election. The cost would benefit from the candidate’s election, voters will rank of a candidate is his sum of distances to all voters, and the candidates by increasing distance, a model known as single- distortion of an election is the ratio between the cost of the peaked preferences (Black 1948; Downs 1957; Black 1958; elected candidate and the cost of the optimum candidate. We Moulin 1980; Merrill and Grofman 1999; Barbera,` Gul, consider the case when candidates are representative of the and Stacchetti 1993; Richards, Richards, and McKay 1998; population, in the sense that they are drawn i.i.d. from the Barbera` 2001). population of the voters, and analyze the expected distortion Even in the absence of strategic voting, voting systems of positional voting rules. -
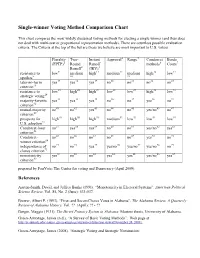
Single-Winner Voting Method Comparison Chart
Single-winner Voting Method Comparison Chart This chart compares the most widely discussed voting methods for electing a single winner (and thus does not deal with multi-seat or proportional representation methods). There are countless possible evaluation criteria. The Criteria at the top of the list are those we believe are most important to U.S. voters. Plurality Two- Instant Approval4 Range5 Condorcet Borda (FPTP)1 Round Runoff methods6 Count7 Runoff2 (IRV)3 resistance to low9 medium high11 medium12 medium high14 low15 spoilers8 10 13 later-no-harm yes17 yes18 yes19 no20 no21 no22 no23 criterion16 resistance to low25 high26 high27 low28 low29 high30 low31 strategic voting24 majority-favorite yes33 yes34 yes35 no36 no37 yes38 no39 criterion32 mutual-majority no41 no42 yes43 no44 no45 yes/no 46 no47 criterion40 prospects for high49 high50 high51 medium52 low53 low54 low55 U.S. adoption48 Condorcet-loser no57 yes58 yes59 no60 no61 yes/no 62 yes63 criterion56 Condorcet- no65 no66 no67 no68 no69 yes70 no71 winner criterion64 independence of no73 no74 yes75 yes/no 76 yes/no 77 yes/no 78 no79 clones criterion72 81 82 83 84 85 86 87 monotonicity yes no no yes yes yes/no yes criterion80 prepared by FairVote: The Center for voting and Democracy (April 2009). References Austen-Smith, David, and Jeffrey Banks (1991). “Monotonicity in Electoral Systems”. American Political Science Review, Vol. 85, No. 2 (June): 531-537. Brewer, Albert P. (1993). “First- and Secon-Choice Votes in Alabama”. The Alabama Review, A Quarterly Review of Alabama History, Vol. ?? (April): ?? - ?? Burgin, Maggie (1931). The Direct Primary System in Alabama. -

A Canadian Model of Proportional Representation by Robert S. Ring A
Proportional-first-past-the-post: A Canadian model of Proportional Representation by Robert S. Ring A thesis submitted to the School of Graduate Studies in partial fulfilment of the requirements for the degree of Master of Arts Department of Political Science Memorial University St. John’s, Newfoundland and Labrador May 2014 ii Abstract For more than a decade a majority of Canadians have consistently supported the idea of proportional representation when asked, yet all attempts at electoral reform thus far have failed. Even though a majority of Canadians support proportional representation, a majority also report they are satisfied with the current electoral system (even indicating support for both in the same survey). The author seeks to reconcile these potentially conflicting desires by designing a uniquely Canadian electoral system that keeps the positive and familiar features of first-past-the- post while creating a proportional election result. The author touches on the theory of representative democracy and its relationship with proportional representation before delving into the mechanics of electoral systems. He surveys some of the major electoral system proposals and options for Canada before finally presenting his made-in-Canada solution that he believes stands a better chance at gaining approval from Canadians than past proposals. iii Acknowledgements First of foremost, I would like to express my sincerest gratitude to my brilliant supervisor, Dr. Amanda Bittner, whose continuous guidance, support, and advice over the past few years has been invaluable. I am especially grateful to you for encouraging me to pursue my Master’s and write about my electoral system idea. -
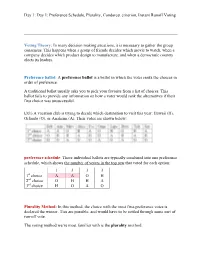
Preference Schedule, Plurality, Condorcet Criterion, Instant Runoff Voting
Day 1: Day 1: Preference Schedule, Plurality, Condorcet criterion, Instant Runoff Voting Voting Theory: In many decision making situations, it is necessary to gather the group consensus. This happens when a group of friends decides which movie to watch, when a company decides which product design to manufacture, and when a democratic country elects its leaders. Preference ballot: A preference ballot is a ballot in which the voter ranks the choices in order of preference. A traditional ballot usually asks you to pick your favorite from a list of choices. This ballot fails to provide any information on how a voter would rank the alternatives if their first choice was unsuccessful. Ex1) A vacation club is trying to decide which destination to visit this year: Hawaii (H), Orlando (O), or Anaheim (A). Their votes are shown below: preference schedule: These individual ballots are typically combined into one preference schedule, which shows the number of voters in the top row that voted for each option: 1 3 3 3 1st choice A A O H 2nd choice O H H A 3rd choice H O A O Plurality Method: In this method, the choice with the most first-preference votes is declared the winner. Ties are possible, and would have to be settled through some sort of run-off vote. The voting method we’re most familiar with is the plurality method. For the plurality method, we only care about the first choice options. Totaling them up: A: Anaheim: 1+3 = 4 first-choice votes O: Orlando: 3 first-choice votes H: Hawaii: 3 first-choice votes Anaheim is the winner using the plurality voting method. -

Majority and Condorcet Criteria Majority Criterion Condorcet Criterion
1 Majority and Condorcet Criteria Majority Criterion If candidate X has a majority of the first-place votes, then candidate X should be the winner of the election. The Plurality Method never violates the Majority Criterion. Condorcet Criterion If there is a choice that in a head-to-head comparison is preferred by the voters over every other choice, then that choice should be the winner of the election. Finding the Condorcet Candidate: Do a Head-to-head comparison: Compare two candidates, then another two, until all pairs of candidates have been considered. Is there one candidate that is always preferred? If so, that candidate is the Condorcet Candidate. Example: Number of voters 49 48 3 First choice RHF Second choice HSH Third choice FOS Fourth choice OFO Fifth choice SRR We could compare the candidates one-on-one, but this would mean 24 head-to-head comparisons! Instead, notice candidate H is near the top and just look at comparisions involving H. H vs. R 49 48 3 H vs. F 49 48 3 1st RHH 1st HHF 2nd HRR 2nd FFH H vs. O 49 48 3 H vs. S 49 48 3 1st HHH 1st HHH 2nd OOO 2nd SSS 2 When we compare just H and R, 49 people prefer R to H and 51 prefer H to R. When we compare just H and F, 97 people prefer H to F and 3 prefer H to F. When we compare just H and O, 100 people prefer H to O. When we compare just H and S, 100 people prefer H to S. -

Another Consideration in Minority Vote Dilution Remedies: Rent
Another C onsideration in Minority Vote Dilution Remedies : Rent -Seeking ALAN LOCKARD St. Lawrence University In some areas of the United States, racial and ethnic minorities have been effectively excluded from the democratic process by a variety of means, including electoral laws. In some instances, the Courts have sought to remedy this problem by imposing alternative voting methods, such as cumulative voting. I examine several voting methods with regard to their sensitivity to rent-seeking. Methods which are less sensitive to rent-seeking are preferred because they involve less social waste, and are less likely to be co- opted by special interest groups. I find that proportional representation methods, rather than semi- proportional ones, such as cumulative voting, are relatively insensitive to rent-seeking efforts, and thus preferable. I also suggest that an even less sensitive method, the proportional lottery, may be appropriate for use within deliberative bodies, where proportional representation is inapplicable and minority vote dilution otherwise remains an intractable problem. 1. INTRODUCTION When President Clinton nominated Lani Guinier to serve in the Justice Department as Assistant Attorney General for Civil Rights, an opportunity was created for an extremely valuable public debate on the merits of alternative voting methods as solutions to vote dilution problems in the United States. After Prof. Guinier’s positions were grossly mischaracterized in the press,1 the President withdrew her nomination without permitting such a public debate to take place.2 These issues have been discussed in academic circles,3 however, 1 Bolick (1993) charges Guinier with advocating “a complex racial spoils system.” 2 Guinier (1998) recounts her experiences in this process. -

Voting Procedures and Their Properties
Voting Theory AAAI-2010 Voting Procedures and their Properties Ulle Endriss 8 Voting Theory AAAI-2010 Voting Procedures We’ll discuss procedures for n voters (or individuals, agents, players) to collectively choose from a set of m alternatives (or candidates): • Each voter votes by submitting a ballot, e.g., the name of a single alternative, a ranking of all alternatives, or something else. • The procedure defines what are valid ballots, and how to aggregate the ballot information to obtain a winner. Remark 1: There could be ties. So our voting procedures will actually produce sets of winners. Tie-breaking is a separate issue. Remark 2: Formally, voting rules (or resolute voting procedures) return single winners; voting correspondences return sets of winners. Ulle Endriss 9 Voting Theory AAAI-2010 Plurality Rule Under the plurality rule each voter submits a ballot showing the name of one alternative. The alternative(s) receiving the most votes win(s). Remarks: • Also known as the simple majority rule (6= absolute majority rule). • This is the most widely used voting procedure in practice. • If there are only two alternatives, then it is a very good procedure. Ulle Endriss 10 Voting Theory AAAI-2010 Criticism of the Plurality Rule Problems with the plurality rule (for more than two alternatives): • The information on voter preferences other than who their favourite candidate is gets ignored. • Dispersion of votes across ideologically similar candidates. • Encourages voters not to vote for their true favourite, if that candidate is perceived to have little chance of winning. Ulle Endriss 11 Voting Theory AAAI-2010 Plurality with Run-Off Under the plurality rule with run-off , each voter initially votes for one alternative. -

And the Loser Is... Plurality Voting Jean-François Laslier
And the loser is... Plurality Voting Jean-François Laslier To cite this version: Jean-François Laslier. And the loser is... Plurality Voting. 2011. hal-00609810 HAL Id: hal-00609810 https://hal.archives-ouvertes.fr/hal-00609810 Preprint submitted on 20 Jul 2011 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. ECOLE POLYTECHNIQUE CENTRE NATIONAL DE LA RECHERCHE SCIENTIFIQUE AND THE LOSER IS... PLURALITY VOTING Jean-François LASLIER Cahier n° 2011-13 DEPARTEMENT D'ECONOMIE Route de Saclay 91128 PALAISEAU CEDEX (33) 1 69333033 http://www.economie.polytechnique.edu/ mailto:[email protected] And the loser is... Plurality Voting Jean-Franc¸ois Laslier Abstract This paper reports on a vote for choosing the best voting rules that was organized among the participants of the Voting Procedures workshop in July, 2010. Among 18 voting rules, Approval Voting won the contest, and Plurality Voting re- ceived no support at all. 1 Introduction Experts have different opinions as to which is the best voting procedure. The Lever- hulme Trust sponsored 2010 Voting Power in Practice workshop, held at the Chateau du Baffy, Normandy, from 30 July to 2 August 2010, was organized for the purpose of discussing this matter. -

14 Multiparty Split-Ticket Voting Estimation As an Ecological Inference Problem∗
P1: JMT CB658-14 CB654-KING-Sample CB658-KING-Sample.cls April 28, 2004 12:26 14 Multiparty Split-Ticket Voting Estimation as an Ecological Inference Problem∗ Kenneth Benoit, Michael Laver, and Daniela Giannetti ABSTRACT The estimation of vote splitting in mixed-member electoral systems is a common problem in electoral studies, where the goal of researchers is to estimate individual voter transitions between parties on two different ballots cast simultaneously. Because the ballots are cast separately and secretly, however, voter choice on the two ballots must be recreated from separately tabulated aggregate data. The problem is therefore of one of making ecological inferences. Because of the multiparty contexts normally found where mixed-member electoral rules are used, furthermore, the problem involves large-table (R × C) ecological inference. In this chapter we show how vote-splitting problems in multiparty systems can be formulated as ecological inference problems and adapted for use with King’s (1997) ecological inference procedure. We demonstrate this process by estimating vote splitting in the 1996 Italian legislative elections between voters casting party-based list ballots in proportional representation districts and candidate-based plurality ballots in single-member districts. Our example illustrates the pitfalls and payoffs of estimating vote splitting in multiparty contexts, and points to directions for future research in multiparty voting contexts using R × C ecological inference. INTRODUCTION Split-ticketvotingisacommonfocusofinterestinthefieldofelectoralstudies.Itisconcerned