The Phenomenon of the Galaxy NGC 6286: a Forming Polar Ring Or A
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

XIII Publications, Presentations
XIII Publications, Presentations 1. Refereed Publications E., Kawamura, A., Nguyen Luong, Q., Sanhueza, P., Kurono, Y.: 2015, The 2014 ALMA Long Baseline Campaign: First Results from Aasi, J., et al. including Fujimoto, M.-K., Hayama, K., Kawamura, High Angular Resolution Observations toward the HL Tau Region, S., Mori, T., Nishida, E., Nishizawa, A.: 2015, Characterization of ApJ, 808, L3. the LIGO detectors during their sixth science run, Classical Quantum ALMA Partnership, et al. including Asaki, Y., Hirota, A., Nakanishi, Gravity, 32, 115012. K., Espada, D., Kameno, S., Sawada, T., Takahashi, S., Ao, Y., Abbott, B. P., et al. including Flaminio, R., LIGO Scientific Hatsukade, B., Matsuda, Y., Iono, D., Kurono, Y.: 2015, The 2014 Collaboration, Virgo Collaboration: 2016, Astrophysical Implications ALMA Long Baseline Campaign: Observations of the Strongly of the Binary Black Hole Merger GW150914, ApJ, 818, L22. Lensed Submillimeter Galaxy HATLAS J090311.6+003906 at z = Abbott, B. P., et al. including Flaminio, R., LIGO Scientific 3.042, ApJ, 808, L4. Collaboration, Virgo Collaboration: 2016, Observation of ALMA Partnership, et al. including Asaki, Y., Hirota, A., Nakanishi, Gravitational Waves from a Binary Black Hole Merger, Phys. Rev. K., Espada, D., Kameno, S., Sawada, T., Takahashi, S., Kurono, Lett., 116, 061102. Y., Tatematsu, K.: 2015, The 2014 ALMA Long Baseline Campaign: Abbott, B. P., et al. including Flaminio, R., LIGO Scientific Observations of Asteroid 3 Juno at 60 Kilometer Resolution, ApJ, Collaboration, Virgo Collaboration: 2016, GW150914: Implications 808, L2. for the Stochastic Gravitational-Wave Background from Binary Black Alonso-Herrero, A., et al. including Imanishi, M.: 2016, A mid-infrared Holes, Phys. -

Nustar Unveils a Heavily Obscured Low-Luminosity Active Galactic Nucleus in the Luminous Infrared Galaxy Ngc 6286 C
Draft version October 26, 2015 A Preprint typeset using LTEX style emulateapj v. 04/17/13 NUSTAR UNVEILS A HEAVILY OBSCURED LOW-LUMINOSITY ACTIVE GALACTIC NUCLEUS IN THE LUMINOUS INFRARED GALAXY NGC 6286 C. Ricci1,2,*, et al. Draft version October 26, 2015 ABSTRACT We report on the detection of a heavily obscured Active Galactic Nucleus (AGN) in the Lumi- nous Infrared Galaxy (LIRG) NGC 6286, obtained thanks to a 17.5 ks NuSTAR observation of the source, part of our ongoing NuSTAR campaign aimed at observing local U/LIRGs in different merger stages. NGC6286 is clearly detected above 10keV and, by including the quasi-simultaneous Swift/XRT and archival XMM-Newton and Chandra data, we find that the source is heavily obscured 24 −2 [N H ≃ (0.95 − 1.32) × 10 cm ], with a column density consistent with being mildly Compton- −2 thick [CT, log(N H/cm ) ≥ 24]. The AGN in NGC 6286 has a low absorption-corrected luminosity 41 −1 (L2−10 keV ∼ 3 − 20 × 10 ergs ) and contributes .1% to the energetics of the system. Because of its low-luminosity, previous observations carried out in the soft X-ray band (< 10 keV) and in the in- frared excluded the presence of a buried AGN. NGC 6286 has multi-wavelength characteristics typical of objects with the same infrared luminosity and in the same merger stage, which might imply that there is a significant population of obscured low-luminosity AGN in LIRGs that can only be detected by sensitive hard X-ray observations. 1. INTRODUCTION 2012; Schawinski et al. -

The Applicability of Far-Infrared Fine-Structure Lines As Star Formation
A&A 568, A62 (2014) Astronomy DOI: 10.1051/0004-6361/201322489 & c ESO 2014 Astrophysics The applicability of far-infrared fine-structure lines as star formation rate tracers over wide ranges of metallicities and galaxy types? Ilse De Looze1, Diane Cormier2, Vianney Lebouteiller3, Suzanne Madden3, Maarten Baes1, George J. Bendo4, Médéric Boquien5, Alessandro Boselli6, David L. Clements7, Luca Cortese8;9, Asantha Cooray10;11, Maud Galametz8, Frédéric Galliano3, Javier Graciá-Carpio12, Kate Isaak13, Oskar Ł. Karczewski14, Tara J. Parkin15, Eric W. Pellegrini16, Aurélie Rémy-Ruyer3, Luigi Spinoglio17, Matthew W. L. Smith18, and Eckhard Sturm12 1 Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281 S9, 9000 Gent, Belgium e-mail: [email protected] 2 Zentrum für Astronomie der Universität Heidelberg, Institut für Theoretische Astrophysik, Albert-Ueberle Str. 2, 69120 Heidelberg, Germany 3 Laboratoire AIM, CEA, Université Paris VII, IRFU/Service d0Astrophysique, Bat. 709, 91191 Gif-sur-Yvette, France 4 UK ALMA Regional Centre Node, Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy, University of Manchester, Oxford Road, Manchester M13 9PL, UK 5 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK 6 Laboratoire d0Astrophysique de Marseille − LAM, Université Aix-Marseille & CNRS, UMR7326, 38 rue F. Joliot-Curie, 13388 Marseille CEDEX 13, France 7 Astrophysics Group, Imperial College, Blackett Laboratory, Prince Consort Road, London SW7 2AZ, UK 8 European Southern Observatory, Karl -

Interstellarum 52 • Juni/Juli 2007 1 Inhalt
Editorial fokussiert Liebe Leserinnen und Leser, gibt es tatsächlich Planeten um andere Sterne, die die Vorrausset- zungen für die Entwicklung von Leben erfüllen? Eine derartige Mel- dung machte Ende April die Runde, als die ESO die Entdeckung eines Planeten in der »bewohnbaren«, weil möglicherweise die Existenz fl üs- sigen Wassers erlaubenden Zone um den Stern Gliese 581 bekanntgab (Seite 18). Solche Berichte machen den Eindruck, die Entdeckung von Leben in anderen Sonnensystemen stehe unmittelbar bevor – doch Daniel Fischers Blick hinter die Kulissen zeigt, dass wir noch am Anfang der Suche nach Exoplaneten stehen (Seite 12). Wenn interstellarum Teleskope testet, dann richtig – mit mehrmo- natigem Praxistest und optischer Bank. Diesmal stehen drei apochro- Ronald Stoyan, Chefredakteur matische Refraktoren der neuen Generation auf dem Prüfstand, die die Entscheidung besonders schwer machen – und die Beurteilung zu einem Vergnügen für den Tester. In diesem Heft steht die visuelle Leis- tungsfähigkeit im Vordergrund (Seite 50), in der kommenden Ausgabe werden die fotografi schen Fähigkeiten nachgereicht. Übrigens: Falls Sie einen Fernrohr-Kauf planen, empfehle ich Ihnen unsere Neuer- scheinung »Fernrohrwahl«. Dort sind praktisch alle auf dem deutschen Markt erhältlichen Modelle tabellarisch aufgelistet. Neu im Verlagsprogramm ist ebenfalls eine neue Ausgabe der inter- stellarum Archiv-CD, diesmal mit PDF-Dokumenten der Heftnummern 32 bis 49 – bestellbar über unsere Internetseite www.interstellarum.de. Dort laden wir Sie auch zur Teilnahme an der bisher größten Leserum- frage unserer Geschichte ein, denn wir wollen mehr über Sie und Ihre astronomischen Vorlieben erfahren – natürlich anonym. Bitte helfen Sie uns, interstellarum noch mehr auf Ihre Bedürfnisse auszurichten. Ihr Titelbild: Wie ein Planet eines anderen Sterns aussieht ist reine Spekulation – doch die künstlerische Darstellung der ESO hilft der Vorstellungskraft auf die Sprünge. -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

Arp Catalogue.Xlsx
ATLAS OF PECULIAR GALAXIES CATALOGUE 1 ATLAS OF PECULIAR GALAXIES CATALOGUE Object Name Mag RA Dec Constellation ARP 1 NGC 2857 12.2 09:24:37 49:21:00 Ursa Major ARP 2 13.2 16:16:18 47:02:00 Hercules ARP 3 13.4 22:36:34 ‐02:54:00 Aquarius ARP 4 13.7 01:48:25 ‐12:22:00 Cetus ARP 5 NGC 3664 12.8 11:24:24 03:19:00 Leo ARP 6 NGC 2537 12.3 08:13:14 45:59:00 Lynx ARP 7 14.5 08:50:17 ‐16:34:00 Hydra ARP 8 NGC 0497 13 01:22:23 ‐00:52:00 Cetus ARP 9 NGC 2523 11.9 08:14:59 73:34:00 Camelopardalis ARP 10 13.8 02:18:26 05:39:00 Cetus ARP 11 14.4 01:09:23 14:20:00 Pisces ARP 12 NGC 2608 12.2 08:35:17 28:28:00 Cancer ARP 13 NGC 7448 11.6 23:00:02 15:59:00 Pegasus ARP 14 NGC 7314 10.9 22:35:45 ‐26:03:00 Pisces Austrinus ARP 15 NGC 7393 12.6 22:51:39 ‐05:33:00 Aquarius ARP 16 M66 8.9 11:20:14 12:59:00 Leo ARP 17 14.7 07:44:32 73:49:00 Camelopardalis ARP 17 07:44:38 73:48:00 Camelopardalis ARP 18 NGC 4088 10.5 12:05:35 50:32:00 Ursa Major ARP 19 NGC 0145 13.2 00:31:45 ‐05:09:00 Cetus ARP 20 14.4 04:19:53 02:05:00 Taurus ARP 21 14.7 11:04:58 30:01:00 Leo Minor ARP 22 14.9 11:59:29 ‐19:19:00 Corvus ARP 22 NGC 4027 11.2 11:59:30 ‐19:15:00 Corvus ARP 23 NGC 4618 10.8 12:41:32 41:09:00 Canes Venatici ARP 24 NGC 3445 12.6 10:54:36 56:59:00 Ursa Major ARP 24 12.8 10:54:45 56:57:00 Ursa Major ARP 25 NGC 2276 11.4 07:27:13 85:45:00 Cepheus ARP 26 M101 7.9 14:03:12 54:21:00 Ursa Major ARP 27 NGC 3631 10.4 11:21:02 53:10:00 Ursa Major ARP 28 NGC 7678 11.8 23:28:27 22:25:00 Pegasus ARP 29 NGC 6946 8.8 20:34:52 60:09:00 Cygnus ARP 30 NGC 6365 12.2 17:22:42 62:10:00 -

June 2013 Volume 24 Number 6 - the Official Publication of the San Jose Astronomical Association
The Ephemeris June 2013 Volume 24 Number 6 - The Official Publication of the San Jose Astronomical Association. Houge Park June Events From the Editor - Mina Wagner 6/2 Hello friends! Summer is fast approaching and Solar observing. 2 - 4 p.m. Star Party season is just around the corner. It’s Fix-It Day 2 - 4 p.m. time to get the telescopes out, clean them, review your observing accessories, cold-weather 6/14 clothes, favorite snacks and drinks, thermoses, Star party. 9:30 p.m. - midnight. etc. One major star party already took place, the Texas Star Party (TSP) in the West Texas desert, and the Golden State Star Party (GSSP) begins on July 6th in north-east California. 6/21 Beginners Imaging Group 7:30 - 9 pm If you have never been to GSSP you should treat yourself this year. The skies are very dark, the scenery spectacular, and the Albaughs, our hosts, make it feel like a family affair. 6/22 General Meeting Please check our website: sjaa.net for updates on local weekend star parties. If you have 7:30 - 8 p.m. Social time pot luck never joined us for those you should go to one. Bring your telescope, or just bring yourself. 8 - 10 p.m. Speaker: Dr. Dana Backman, Children will love the experience and will never forget it. You can look through other peo- “SOPHIA—Science from 41,000 Feet”. ple's telescopes and share a nice evening of observing. Don't forget your jacket and snacks. 6/28 If you have any ideas about an observing trip, maybe you want to share them and we can 7 to 8:15 p.m. -
![Arxiv:1707.07134V1 [Astro-Ph.GA] 22 Jul 2017 2 Radio-Selected AGN](https://docslib.b-cdn.net/cover/5124/arxiv-1707-07134v1-astro-ph-ga-22-jul-2017-2-radio-selected-agn-2715124.webp)
Arxiv:1707.07134V1 [Astro-Ph.GA] 22 Jul 2017 2 Radio-Selected AGN
Astronomy Astrophysics Review manuscript No. (will be inserted by the editor) Active Galactic Nuclei: what’s in a name? P. Padovani · D. M. Alexander · R. J. Assef · B. De Marco · P. Giommi · R. C. Hickox · G. T. Richards · V. Smolciˇ c´ · E. Hatziminaoglou · V. Mainieri · M. Salvato Received: June 12, 2017 / Accepted: July 21, 2017 Abstract Active Galactic Nuclei (AGN) are energetic as- sic differences between AGN, and primarily reflect varia- trophysical sources powered by accretion onto supermassive tions in a relatively small number of astrophysical parame- black holes in galaxies, and present unique observational ters as well the method by which each class of AGN is se- signatures that cover the full electromagnetic spectrum over lected. Taken together, observations in different electromag- more than twenty orders of magnitude in frequency. The netic bands as well as variations over time provide comple- rich phenomenology of AGN has resulted in a large number mentary windows on the physics of different sub-structures of different “flavours” in the literature that now comprise a in the AGN. In this review, we present an overview of AGN complex and confusing AGN “zoo”. It is increasingly clear multi-wavelength properties with the aim of painting their that these classifications are only partially related to intrin- “big picture” through observations in each electromagnetic band from radio to γ-rays as well as AGN variability. We P. Padovani · E. Hatziminaoglou · V. Mainieri address what we can learn from each observational method, European Southern Observatory, Karl-Schwarzschild-Str. 2, D-85748 the impact of selection effects, the physics behind the emis- Garching bei Munchen,¨ Germany sion at each wavelength, and the potential for future studies. -

Arp's Peculiar Galaxies - Supplementary Index the Deep Space CCD Atlas: North Presents 153 of the 338 Views Selected by Halton C
Arp's Peculiar Galaxies - Supplementary Index The Deep Space CCD Atlas: North presents 153 of the 338 views selected by Halton C. Arp in his 1966 Atlas of Peculiar Galaxies. An asterisk (*) indicates that the galaxy is not identified by its Arp number in the CCD Atlas or its index. The headings are the categories (a "preliminary" taxonomy) Arp established with his 1966 Atlas. Arp Common name Page Arp Common name Page Arp Common name Page Spiral Galaxies: 116 MESSIER 60 143 239 NGC 5278 + 79 152 LOW SURFACE BRIGHTNESS 120 NGC 4438 + 35 134* 240 NGC 5257 + 58 152 1 NGC 2857 99 122 NGC 6040A + B 167* 242 The Mice 143 2 UGC 10310 168* 123 NGC 1888 + 89 49 243 NGC 2623 93 3 MCG-01-57-016 245 124 NGC 6361 + comp 177* 244 NGC 4038 + 39 123* 5 NGC 3664 116 WITH NEARBY FRAGMENTS 245 NGC 2992 + 93 101 6 NGC 2537 90* 133 NGC 0541 15* 246 NGC 7838 + 37 1* SPLIT ARM 134 MESSIER 49 136* 248 Wild's Triplet 120 8 NGC 0497 14 135 NGC 1023 29* IRREGULAR CLUMPS 9 NGC 2523 91* 136 NGC 5820 161* 259 NGC 1741 group 47 12 NGC 2608 92* MATERIAL EMANATING FROM E 263 NGC 3239 107 DETACHED SEGMENTS GALAXIES 264 NGC 3104 104 13 NGC 7448 248* 137 NGC 2914 99* 266 NGC 4861 147 14 NGC 7314 245* 140 NGC 0275 + 74 9* 268 Holmberg II 91 15 NGC 7393 247 142 NGC 2936 + 37 100 16 MESSIER 66 114* 143 NGC 2444 + 45 85 Group Character 18 NGC 4088 124* CONNECTED ARMS THREE-ARMED Galaxies 269 NGC 4490 + 85 136* 19 NGC 0145 3 WITH ASSOCIATED RINGS 270 NGC 3395 + 96 110* 22 NGC 4027 123* 148 Mayall's Object 112 271 NGC 5426 + 27 156 ONE-ARMED WITH JETS 272 NGC 6050 + IC1174 168* -

Star Formation and Nuclear Activity of Local Luminous Infrared Galaxies
PhD Thesis Star Formation and Nuclear Activity of Local Luminous Infrared Galaxies Memoria de tesis doctoral presentada por D. Miguel Pereira Santaella para optar al grado de Doctor en Ciencias F´ısicas Universidad Aut´onoma Consejo Superior de Madrid de Investigaciones Cient´ıficas Facultad de Ciencias Instituto de Estructura de la Materia Departamento de F´ısica Te´orica Centro de Astrobiolog´ıa Madrid, noviembre de 2011 Directora: Dra. Almudena Alonso Herrero Instituto de F´ısica de Cantabria Tutora: Prof.ª Rosa Dom´ınguez Tenreiro Universidad Aut´onoma de Madrid Agradecimientos En primer lugar quer´ıadar las gracias a mi directora de tesis, Almudena Alonso Herrero, por haber confiado en mi desde un principio para realizar este trabajo, as´ı como por todo su inter´es y dedicaci´on durante estos cuatro a˜nos. Adem´as me gustar´ıa agradecer la ayuda y consejos de Luis Colina. En este tiempo he tenido la oportunidad de realizar estancias en centros de in- vestigaci´on extranjeros de los que guardo un grato recuerdo personal y cient´ıfico. En particular me gustar´ıaagradecer a George Rieke y a Martin Ward su hospitalidad y amabilidad durante mis visitas al Steward Observatory en la Universidad de Arizona y a la Universidad de Durham. Y volviendo a Madrid, quisiera agradecer a Tanio y a Marce el apoyo y la ayuda que me ofrecieron en los inciertos comienzos de este proyecto. Tambi´en quiero dar las gra- cias a todos (Arancha, Nuria, Alvaro,´ Alejandro, Julia, Jairo, Javier, Ruym´an, Fabi´an, entre otros) por las interesantes conversaciones, a veces incluso sobre ciencia, en las sobremesas, caf´es, etc. -

Research Collection
Research Collection Doctoral Thesis The varying activity of supermassive black holes on multiple timescales Author(s): Sartori, Lia Publication Date: 2019 Permanent Link: https://doi.org/10.3929/ethz-b-000382815 Rights / License: In Copyright - Non-Commercial Use Permitted This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use. ETH Library DISS. ETH NO. 26133 The varying activity of supermassive black holes on multiple timescales A thesis submitted to attain the degree of DOCTOR OF SCIENCES of ETH ZURICH (Dr. sc. ETH Zurich) presented by Lia Federica Sartori Master of Science ETH in Physics ETH Zurich born on October 26, 1990 citizen of Bosco/Gurin (TI), Switzerland accepted on the recommendation of Prof. Dr. Alexandre Refregier Dr. Kevin Schawinski Prof. Dr. Ezequiel Treister 2019 Per la mia famiglia Vargaltsgott Abstract Variable emission is a ubiquitous property of active galactic nuclei (AGN). It can be observed or inferred at essentially all timescales, from hours to billions of years, and across the entire electromagnetic spectrum. Since most of the AGN luminosity originates from the accretion of matter into the central supermassive black hole (SMBH), the study of AGN variability can provide crucial information about the physics and structure of the central engine, including at spatial scales that are beyond the resolving power of most of the observing facilities for the majority of the AGN. In addition, the study of AGN variability allows us to probe the close link between SMBHs and their host galaxies by taking into account the fact that the energy injection from the AGN varies with time. -
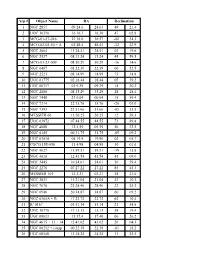
Arp # Object Name 1 NGC 2857 09 24.6 24.63 49 21.4 2 UGC 10310
Arp # Object Name RA Declination 1 NGC 2857 09 24.6 24.63 49 21.4 2 UGC 10310 16 16.3 16.30 47 02.8 3 MCG-01-57-016 22 36.6 36.57 -02 54.3 4 MCG-02-05-50 + A 01 48.4 48.43 -12 22.9 5 NGC 3664 11 24.41 24.41 03 19.6 6 NGC 2537 08 13.24 13.24 45 59.5 7 MCG-03-23-009 08 50.29 50.29 -16 34.6 8 NGC 0497 01 22.39 22.39 00 52.5 9 NGC 2523 08 14.99 14.99 73 34.8 10 UGC 01775 02 18.44 18.44 05 39.2 11 UGC 00717 01 9.39 09.39 14 20.2 12 NGC 2608 08 35.29 35.29 28 28.4 13 NGC 7448 23 0.04 00.04 15 59.4 14 NGC 7314 22 35.76 35.76 -26 03.0 15 NGC 7393 22 51.66 51.66 -05 33.5 16 MESSIER 66 11 20.25 20.25 12 59.3 17 UGC 03972 07 44.55 44.55 73 49.8 18 NGC 4088 12 5.59 05.59 50 32.5 19 NGC 0145 00 31.75 31.75 -05 09.2 20 UGC 03014 04 19.9 19.90 02 05.7 21 CGCG 155-056 11 4.98 04.98 30 01.6 22 NGC 4027 11 59.51 59.51 -19 15.8 23 NGC 4618 12 41.54 41.54 41 09.0 24 NGC 3445 10 54.61 54.61 56 59.4 25 NGC 2276 07 27.22 27.22 85 45.3 26 MESSIER 101 14 3.21 03.21 54 21.0 27 NGC 3631 11 21.04 21.04 53 10.3 28 NGC 7678 23 28.46 28.46 22 25.3 29 NGC 6946 20 34.87 34.87 60 09.2 30 NGC 6365A + B 17 22.72 22.72 62 10.4 31 IC 0167 01 51.14 51.14 21 54.8 32 UGC 10770 17 13.13 13.13 59 19.4 33 UGC 08613 13 37.4 37.40 06 26.2 34 NGC 4615 + 13 + 14 12 41.62 41.62 26 04.3 35 UGC 00212 + comp 00 22.38 22.38 -01 18.2 36 UGC 08548 13 34.25 34.25 31 25.5 37 MESSIER 77 02 42.68 42.68 00 00.8 38 NGC 6412 17 29.6 29.60 75 42.3 39 NGC 1347 03 29.7 29.70 -22 16.7 40 IC 4271 13 29.34 29.34 37 24.5 41 NGC 1232 + A 03 9.76 09.76 -20 34.7 42 NGC 5829 + IC 4526 15 2.7 02.70 23 19.9 43