DOCSLIB.ORG

Lecture 31 Notes (PDF)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture 31 Notes (PDF) Superposition and Interference Physics 111 Waves of small amplitude traveling through the Lecture 31 (Walker: 14.7-8) same medium combine, or superpose, by simple addition. Neither wave affects the other, Wave Superposition but they both affect the total disturbance. Wave Interference Standing Waves Physics of Musical Instruments Temperature Nov. 30, 2009 Lecture 31 1/28 Lecture 31 2/28 Superposition and Interference Interference; Principle of Superposition If two pulses combine to give a larger pulse, These figures show the sum of two waves. In have constructive interference (left). If pulses (a) they add constructively; combine to give smaller pulse, have destructive (b) they add destructively; interference (right). (c) they add partially destructively. Lecture 31 3/28 Lecture 31 4/28 Wave Fronts Wave Phase Two- or three-dimensional waves can be •The phase of a wave (at a given point) is the represented by wave fronts, which are curves part of its cycle the wave is in. Often use the of surfaces where all the waves have the same corresponding angle or rotation: phase. Wave fronts are usually crests. Phase Phase Angle (°) Phase angle (rad) x=+A Crest 0 0 Lines perpendicular x=0 after crest 90° π/2 to wave fronts called x= -A Trough 180° π rays; they point in direction of x=0 after trough 270° 3π/2 propagation of the π x= +A rest 360° or 0° 2 or 0 wave. • Two waves with same phase at given place and time give constructive interference Lecture 31 5/28 Lecture 31 6/28 Interference of Waves from 2 Sources If sources “in phase”, points where distance to Interference sources differs by an equal number of of Sound Waves wavelengths (A or C) will interfere constructively; in between (B), interference will be destructive. Sound waves interfere in space in same way that other waves do. Lecture 31 7/28 Standing Waves Standing Waves; Resonance A standing wave is When both ends of a fixed in location, but string are fixed, only oscillates with time. waves which are These waves are found motionless at ends of on strings with both string can persist. These ends fixed, such as in points of zero a musical instrument, disturbance are called and also in vibrating nodes. In between the columns of air. nodes are antinodes, Standing waves occur where disturbance when reflections from amplitude is maximum. the ends interfere The different standing constructively. wave patterns are Lecture 31 9/28 Lecturemodes. 31 10/28 Standing Waves Standing Waves; Resonance The fundamental, or lowest, frequency on a fixed Frequencies of string has wavelength twice the length of string. standing waves on a Higher frequency harmonics have shorter particular string are wavelengths. called resonant frequencies. The lowest resonant frequency f1 is referred to as the fundamental and the higher resonant frequencies fn th = nf1 as the n harmonics. Lecture 31 11/28 Lecture 31 12/28 Standing Waves of Guitar Strings Standing Waves - Fundamental Frequency Thin string In order for different In a piano, the strings vary in both length and strings to have different density. This gives the sound box of a grand fundamental frequencies, piano its characteristic shape. they must differ in length and/or mass/unit length. Once the length and material of the string is decided, individual strings may be tuned to the A guitar has strings that exact desired frequencies by changing the are all the same length, but tension. the mass/unit length varies. Musical instruments are usually designed so We change the effective that the variation in tension between the length of a string by different strings is small; this helps prevent pressing it against the Thick string warping and other damage. fingerboard. Lecture 31 13/28 Lecture 31 14/28 Standing Waves Example • Guitar string of length 0.75 m has m/L = 2x10-4 kg/m. What tension is needed to get a 440 Hz Standing waves can also be fundamental? excited in columns of air, such as soda bottles, f1 = 440 Hz = vw/2L; need vw = 2(0.75m)(440 Hz)=660m/s woodwind instruments, or organ pipes. F v = As indicated in the drawing, w m / L the closed end is a node (N), F = (m/L)(660m/s)2 = (2x10-4kg/m)(4.36x105 and the open end is an m2/s2) antinode (A). = 87N Lecture 31 15/28 Lecture 31 16/28 Standing Waves: Open/Closed Pipe In this case, the fundamental wavelength is four Open/Closed Tube Resonances times the length of the pipe, and only odd- numbered harmonics appear. • Standing waves in a half-closed column of air: Lecture 31 17/28 Lecture 31 18/28 Standing Waves: Open/Open Pipe Open/Open Tube Resonances If the tube is open at both ends, both ends are • Standing waves in a fully open column of antinodes, and the sequence of harmonics is the air: same as that on a string. All harmonics appear. Note that these results are the same as for the fixed string. f2 = 2f1 (Octave above fundamental) f3 = 3f1 (Octave + fifth above fundamental) f4 = 4f1 (Two octaves above fundamental) - Lecture 31 19/28 Lecture 31 20/28 Demo Temperature (T) Random kinetic energies of atoms at different • Temperature (T) is a measure of how “hot” or temperatures. “cold” something is • Temperature is a measure of the random kinetic energy of each particle in an object. – The greater the motion/vibration the greater the T – The smaller the motion/vibration the lower the T • SI Unit: kelvin (K) – E.g., room temperature is about 295K • Kelvin is the natural temperature scale – 0 K is lowest possible temperature – No negative temperatures – Random internal KE is zero at T = 0 K Lecture 31 21/28 Low T liquid. Lecture 31High T liquid. 22/28 The Three Basic Phases of Matter Other Temperature Scales The Celsius scale: Solid Liquid Gas Water freezes at 0° Celsius. Water boils at 100° Celsius. The Fahrenheit scale: Water freezes at 32° Fahrenheit . Water boils at 212° Fahrenheit . Sequence of increasing molecule motion (and energy) Lecture 31 23/28 Lecture 31 24/28 Kelvin Temperature Scale Temperature Scales Compared The Kelvin scale has the same step size (size of one degree) as the Celsius scale, but the Kelvin scale has its zero at absolute zero. Conversion between a Celsius temperature and a Kelvin temperature: Lecture 31 25/28 Lecture 31 26/28 End of Lecture 31 • For Wednesday, Dec. 2, read Walker 16.1-4. • Homework Assignment 14c is due at 11:00 PM on Thursday, Dec. 3. Lecture 31 27/28.
Load more

Recommended publications
  • Experiment 12
    Experiment 12 Velocity and Propagation of Waves 12.1 Objective To use the phenomenon of resonance to determine the velocity of the propagation of waves in taut strings and wires. 12.2 Discussion Any medium under tension or stress has the following property: disturbances, motions of the matter of which the medium consists, are propagated through the medium. When the disturbances are periodic, they are called waves, and when the disturbances are simple harmonic, the waves are sinusoidal and are characterized by a common wavelength and frequency. The velocity of propagation of a disturbance, whether or not it is periodic, depends generally upon the tension or stress in the medium and on the density of the medium. The greater the stress: the greater the velocity; and the greater the density: the smaller the velocity. In the case of a taut string or wire, the velocity v depends upon the tension T in the string or wire and the mass per unit length µ of the string or wire. Theory predicts that the relation should be T v2 = (12.1) µ Most disturbances travel so rapidly that a direct determination of their velocity is not possible. However, when the disturbance is simple harmonic, the sinusoidal character of the waves provides a simple method by which the velocity of the waves can be indirectly determined. This determination involves the frequency f and wavelength λ of the wave. Here f is the frequency of the simple harmonic motion of the medium and λ is from any point of the wave to the next point of the same phase.
    [Show full text]
  • Chapter 5 Waves I: Generalities, Superposition & Standing Waves
    Chapter 5 Waves I: Generalities, Superposition & Standing Waves 5.1 The Important Stuff 5.1.1 Wave Motion Wave motion occurs when the mass elements of a medium such as a taut string or the surface of a liquid make relatively small oscillatory motions but collectively give a pattern which travels for long distances. This kind of motion also includes the phenomenon of sound, where the molecules in the air around us make small oscillations but collectively give a disturbance which can travel the length of a college classroom, all the way to the students dozing in the back. We can even view the up–and–down motion of inebriated spectators of sports events as wave motion, since their small individual motions give rise to a disturbance which travels around a stadium. The mathematics of wave motion also has application to electromagnetic waves (including visible light), though the physical origin of those traveling disturbances is quite different from the mechanical waves we study in this chapter; so we will hold off on studying electromagnetic waves until we study electricity and magnetism in the second semester of our physics course. Obviously, wave motion is of great importance in physics and engineering. 5.1.2 Types of Waves In some types of wave motion the motion of the elements of the medium is (for the most part) perpendicular to the motion of the traveling disturbance. This is true for waves on a string and for the people–wave which travels around a stadium. Such a wave is called a transverse wave. This type of wave is the easiest to visualize.
    [Show full text]
  • Standing Waves Physics Lab I
    Standing Waves Physics Lab I Objective In this series of experiments, the resonance conditions for standing waves on a string will be tested experimentally. Equipment List PASCO SF-9324 Variable Frequency Mechanical Wave Driver, PASCO PI-9587B Digital Frequency Generator, Table Rod, Elastic String, Table Clamp with Pulley, Set of 50 g and 100 g Masses with Mass Holder, Meter Stick. Theoretical Background Consider an elastic string. One end of the string is tied to a rod. The other end is under tension by a hanging mass and pulley arrangement. The string is held taut by the applied force of the hanging mass. Suppose the string is plucked at or near the taut end. The string begins to vibrate. As the string vibrates, a wave travels along the string toward the ¯xed end. Upon arriving at the ¯xed end, the wave is reflected back toward the taut end of the string with the same amount of energy given by the pluck, ideally. Suppose you were to repeatedly pluck the string. The time between each pluck is 1 second and you stop plucking after 10 seconds. The frequency of your pluck is then de¯ned as 1 pluck per every second. Frequency is a measure of the number of repeating cycles or oscillations completed within a de¯nite time frame. Frequency has units of Hertz abbreviated Hz. As you continue to pluck the string you notice that the set of waves travelling back and forth between the taut and ¯xed ends of the string constructively and destructively interact with each other as they propagate along the string.
    [Show full text]
  • Waves and Music
    Team: Waves and Music Part I. Standing Waves Whenever a wave ( sound, heat, light, ...) is confined to a finite region of space (string, pipe, cavity, ... ) , something remarkable happens − the space fills up with a spectrum of vibrating patterns called “standing waves”. Confining a wave “quantizes” the frequency. Standing waves explain the production of sound by musical instruments and the existence of stationary states (energy levels) in atoms and molecules. Standing waves are set up on a guitar string when plucked, on a violin string when bowed, and on a piano string when struck. They are set up in the air inside an organ pipe, a flute, or a saxophone. They are set up on the plastic membrane of a drumhead, the metal disk of a cymbal, and the metal bar of a xylophone. They are set up in the “electron cloud” of an atom. Standing waves are produced when you ring a bell, drop a coin, blow across an empty soda bottle, sing in a shower stall, or splash water in a bathtub. Standing waves exist in your mouth cavity when you speak and in your ear canal when you hear. Electromagnetic standing waves fill a laser cavity and a microwave oven. Quantum-mechanical standing waves fill the space inside atomic systems and nano devices. A. Normal Modes. Harmonic Spectrum. A mass on a spring has one natural frequency at which it freely oscillates up and down. A stretched string with fixed ends can oscillate up and down with a whole spectrum of frequencies and patterns of vibration. Mass on Spring String with Fixed Ends (mass m, spring constant k) (length L, tension F, mass density µ) ___ ___ f = (1/2 π) √k/m f1 = (1/2L) √F/ µ Fundamental nd f2 = 2f 1 2 harmonic rd f3 = 3f 1 3 harmonic th f4 = 4f 1 4 harmonic • • • These special “Modes of Vibration” of a string are called STANDING WAVES or NORMAL MODES .
    [Show full text]
  • Standing Waves
    Chapter 21. Superposition Chapter 21. Superposition The combination of two or more waves is called a superposition of waves. Applications of superposition range from musical instruments to the colors of an oil film to lasers. Chapter Goal: To understand and use the idea of superposition. 1 2 Copyright © 2008 Pearson Education, Inc., publishing as Pearson Addison-Wesley. Copyright © 2008 Pearson Education, Inc., publishing as Pearson Addison-Wesley. Principal of superposition Chapter 21. Superposition Topics: • The Principle of Superposition • Standing Waves • Transverse Standing Waves • Standing Sound Waves and Musical Superimposed Superposition Acoustics N • Interference in One Dimension = + + + = • The Mathematics of Interference Dnet D1 D2 ... DN ∑Di i=1 • Interference in Two and Three Dimensions • Beats 3 4 Copyright © 2008 Pearson Education, Inc., publishing as Pearson Addison-Wesley. Copyright © 2008 Pearson Education, Inc., publishing as Pearson Addison-Wesley. When a wave pulse on a string reflects from a hard boundary, how is the reflected pulse related to the incident pulse? A. Shape unchanged, amplitude unchanged Chapter 21. Reading Quizzes B. Shape inverted, amplitude unchanged C. Shape unchanged, amplitude reduced D. Shape inverted, amplitude reduced E. Amplitude unchanged, speed reduced 5 6 Copyright © 2008 Pearson Education, Inc., publishing as Pearson Addison-Wesley. Copyright © 2008 Pearson Education, Inc., publishing as Pearson Addison-Wesley. When a wave pulse on a string reflects There are some points on a standing from a hard boundary, how is the wave that never move. What are reflected pulse related to the incident these points called? pulse? A. Shape unchanged, amplitude unchanged A. Harmonics B. Shape inverted, amplitude unchanged B.
    [Show full text]
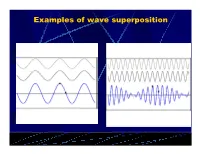
  • Examples of Wave Superposition
    Examples of wave superposition When two waves are traveling in opposite directions, such as when a wave is reflected back on itself, the principle of superposition can be applied at different points on the string. At point A, the two waves cancel each other at all times. At this point, the string will not oscillate at all; this is called a node. At point B, both waves will be in phase at all times. The two waves always add, producing a displacement twice that of each wave by itself. This is called an antinode. This pattern of oscillation is called a standing wave. The waves traveling in opposite directions interfere in a way that produces a standing or fixed pattern. The distance between adjacent nodes or adjacent antinodes is half the wavelength of the original waves. At the nodes, it is not moving at all. At points between the nodes and antinodes, the amplitude has intermediate values. For a string fixed at both ends, the simplest standing wave, the fundamental or first harmonic, has nodes at both ends and an antinode in the middle. v v f 2L The second harmonic has a node at the midpoint of the string, and a wavelength equal to L. v v f L The third harmonic has four nodes (counting the ones at the ends) and three antinodes, and a wavelength v v equal to two-thirds L. f (2 / 3)L 4B-10 MONOCHORD What is the purpose of tightening or loosening the string ? What role do the frets play ? Real Musical Instrument F v v v Chinese Zither f m where 2L L CHANGING TENSION OF THE STRING AFFECTS THE SPEED OF WAVE PROPAGATION AND CHANGES THE FUNDAMENTAL FREQUENCY THE BRIDGE ACTS AS A FRET THAT EFFECTIVELY CHANGES THE LENGTH OF THE WIRE AND THE FUNDAMENTAL FREQUENCY Physics 214 Fall 2010 4/13/2011 5 A guitar string has a mass of 4 g, a length of 74 cm, and a tension of 400 N.
    [Show full text]
  • The Origins of Phantom Partials in the Piano
    Rollins College Rollins Scholarship Online Honors Program Theses Spring 2020 The Origins of Phantom Partials in the Piano Lauren M. Neldner Rollins College, [email protected] Follow this and additional works at: https://scholarship.rollins.edu/honors Part of the Other Physics Commons, and the Statistical, Nonlinear, and Soft Matter Physics Commons Recommended Citation Neldner, Lauren M., "The Origins of Phantom Partials in the Piano" (2020). Honors Program Theses. 105. https://scholarship.rollins.edu/honors/105 This Open Access is brought to you for free and open access by Rollins Scholarship Online. It has been accepted for inclusion in Honors Program Theses by an authorized administrator of Rollins Scholarship Online. For more information, please contact [email protected]. THE ORIGINS OF PHANTOM PARTIALS IN THE PIANO Lauren M. Neldner A Senior Honors Project Submitted in Partial Fulfillment of the Requirements of the Honors Degree Program March 2020 Faculty Sponsor: Thomas R. Moore Rollins College Winter Park, FL Contents Acknowledgments 6 1 Introduction 7 1.1 History of the Piano . 7 1.2 The Modern Piano . 9 1.2.1 Frame and Case . 11 1.2.2 Soundboard . 11 1.2.3 Bridges . 13 1.2.4 Strings . 14 1.2.5 Hammers and Action . 16 1.2.6 Pedals and Dampers . 17 2 Phantom Partials 19 2.1 Historical Context . 20 2.2 Historic Theory of Phantom Partials . 21 2.3 Production in Non-string Components . 25 3 Two Plausible Theories 30 3.1 Pressure Induced Nonlinearity . 30 3.2 Contact Nonlinearity . 33 1 4 Experiments and Results 37 4.1 Pressure experiments .
    [Show full text]
  • Superposition and Standing Waves
    chapter 18 Superposition and Standing Waves . Analysis Model: Waves in Interference . Standing Waves . Analysis Model: Waves Under Boundary Conditions . Resonance . Standing Waves in Air Columns . Standing Waves in Rods and Membranes . Beats: Interference in Time . Nonsinusoidal Wave Patterns The wave model was introduced in the previous two chapters. We have seen that waves are very differ- ent from particles. A particle is of zero size, whereas a wave has a characteristic size, its wavelength. Another important difference between waves and particles is that we can explore the possibility of two or more waves combining at one point in the same medium. Particles can be combined to form extended objects, but the particles must be at different locations. In con- trast, two waves can both be present at the same loca- tion. The ramifications of this possibility are explored Blues master B. B. King takes advantage of standing waves on strings. in this chapter. He changes to higher notes on the guitar by pushing the strings When waves are combined in systems with bound- against the frets on the fingerboard, shortening the lengths of the portions of the strings that vibrate. (AP Images) ary conditions, only certain allowed frequencies can exist and we say the frequencies are quantized. Quan- tization is a notion that is at the heart of quantum mechanics, a subject introduced formally in Chapter . There we show that analysis of waves under boundary condi- tions explains many of the quantum phenomena. In this chapter, we use quantization CHAPTER | Superposition and Standing Waves to understand the behavior of the wide array of musical instruments that are based on strings and air columns.
    [Show full text]
  • Standing Waves on a String PURPOSE
    San Diego Miramar College Physics 197 NAME: _______________________________________ DATE: _________________________ LABORATORY PARTNERS : ______________________________________________________ Standing Waves on a String PURPOSE: To study the relationship among stretching force (FT), wavelength (흺), vibrational frequency (f), linear mass density (µ), and wave velocity (v) in a vibrating string; to observe standing waves and the harmonic frequencies of a stretched string. THEORY: Standing waves can be produced when two waves of identical wavelength, velocity, and amplitude are traveling in opposite directions through the same medium. Standing waves can be established using a stretched string to create a train of waves, set up by a vibrating body, and reflected at the end of the string. Newly generated waves will interfere with the old reflected waves. If the conditions are right, then a standing wave pattern will be created. A Stretched string has many modes of vibration, i.e. standing waves. It may vibrate as a single segment; its length is then equal to one half of the wavelength of the vibrations produced. It may also vibrate in two segments, with a node at each end in the middle; the wavelength produced is then equal to the length of the string. It may also vibrate in a larger number of segments. In every case, the length of the string is some integer multiple of half wavelengths. So, if a string is stretched between two fixed points, the ends are constrained not to move; hence, these are the nodes. In a standing wave the nodes, or the points that do not vibrate, occur every half the wavelength; thus, the ends of the string must correspond to nodes and the whole length of the string must accommodate an integer nymber of half wavelengths.
    [Show full text]
  • A Study to Explore the Effects of Sound Vibrations on Consciousness
    International Journal of Social Work and Human Services Practice Horizon Research Publishing Vol.6. No.3 July, 2018, pp. 75-88 A Study to Explore the Effects of Sound Vibrations on Consciousness Meera Raghu Independent Researcher, New Zealand Abstract Sound is a form of energy produced by cause happiness, joy, courage or calmness, dissonant vibrations caused by movement of particles. Sound can intervals can cause tension, anger, fear or sadness, thereby travel through solids (such as metal, wood, membranes), affecting the emotional aspect of consciousness. liquids (water) and gases (air). The sound vibrations that reach our ear are produced by the movement of particles in Keywords Consciousness, Sound, Vibration, Music, the air surrounding the source of sound. The movement or Emotion, Chladni, Pattern, Energy vibration of particles produces waves of sound. Sound waves are longitudinal and travel in the direction of propagation of vibrations. The pitch of sound is related directly to its frequency, which is given by the number of Introduction vibrations or cycles per second. The higher the pitch of sound, the higher is its frequency, and the lower the pitch, Sound is everywhere. There is perpetual movement and the lower is its frequency. Human ear can hear sounds of action in the world around us, and this produces a variety of frequencies ranging from 20 – 20,000 cycles per second (or sounds, such as those coming from Nature, from animals, Hertz – Hz). Sound waves can be visually seen and studied those generated by humans in the form of speech or music, using ‘Chladni’ plates, which was devised and those that are generated by vehicles, machines, gadgets that experimented by Ernst Chladni, a famous physicist with a are used for comfort, leisure and convenience.
    [Show full text]
  • The Sounds of Music: Science of Musical Scales∗ 1
    SERIES ARTICLE The Sounds of Music: Science of Musical Scales∗ 1. Human Perception of Sound Sushan Konar Both, human appreciation of music and musical genres tran- scend time and space. The universality of musical genres and associated musical scales is intimately linked to the physics of sound, and the special characteristics of human acoustic sensitivity. In this series of articles, we examine the science underlying the development of the heptatonic scale, one of the most prevalent scales of the modern musical genres, both western and Indian. Sushan Konar works on stellar compact objects. She Introduction also writes popular science articles and maintains a Fossil records indicate that the appreciation of music goes back weekly astrophysics-related blog called Monday Musings. to the dawn of human sentience, and some of the musical scales in use today could also be as ancient. This universality of musi- cal scales likely owes its existence to an amazing circularity (or periodicity) inherent in human sensitivity to sound frequencies. Most musical scales are specific to a particular genre of music, and there exists quite a number of them. However, the ‘hepta- 1 1 tonic’ scale happens to have a dominating presence in the world Having seven base notes. music scene today. It is interesting to see how this has more to do with the physics of sound and the physiology of human auditory perception than history. We shall devote this first article in the se- ries to understand the specialities of human response to acoustic frequencies. Human ear is a remarkable organ in many ways. The range of hearing spans three orders of magnitude in frequency, extending Keywords from ∼20 Hz to ∼20,000 Hz (Figure 1) even though the sensitivity String vibration, beat frequencies, consonance-dissonance, pitch, tone.
    [Show full text]
  • The Ideal String
    THE IDEAL STRING Natural Modes Natural Frequencies Vibration Modes for an Ideal Stretched String The Model: • An ideal string has no stiffness and has uniform linear density (µ) throughout. • The restoring force for transverse vibrations is provided solely by the tension (T) in the string. Consequences: • Can support travelling transverse waves with a characteristic speed. T speed of tranverse waves on a string: v = µ T is the tension in Newtons (N) µ is the linear density of the string (kg/m) v is the speed in m/s • The travelling waves can interfere with each other to form standing waves between the points of support of the stretched string. • ONLY CERTAIN SPECIAL WAVELENGTHS WILL ALLOW CONSTRUCTIVE INTERFERENCE OF THE TRAVELLING WAVES. EACH OF THESE WAVELENGTHS CORRESPONDS TO A NATURAL MODE OF THE STRING, AND EACH NATURAL MODE HAS ITS OWN NATURAL FREQENCY. Vibration Modes for an Ideal Stretched String Natural Modes: • Standing waves occur only when the string length, L, is a whole number of half-wavelengths. 2L Allowed wavelengths: λ = n = 1, 2, 3, 4, ......... n n • Each one of these wavelengths has its own particular frequency, given by v = f λ v Allowed frequencies: fn = n = 1, 2, 3, 4, .......... λn • Each one of these allowed frequencies is the natural frequency of one of the natural vibration modes of the string. Note that these frequencies form a harmonic series based on f1 = v/2L • The natural modes each have a node at each end of the string, and n-1 additional nodes along the length of the string.
    [Show full text]