DOCSLIB.ORG

Structural Graph Theory Meets Algorithms: Covering And

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Structural Graph Theory Meets Algorithms: Covering And Structural Graph Theory Meets Algorithms: Covering and Connectivity Problems in Graphs Saeed Akhoondian Amiri Fakult¨atIV { Elektrotechnik und Informatik der Technischen Universit¨atBerlin zur Erlangung des akademischen Grades Doktor der Naturwissenschaften Dr. rer. nat. genehmigte Dissertation Promotionsausschuss: Vorsitzender: Prof. Dr. Rolf Niedermeier Gutachter: Prof. Dr. Stephan Kreutzer Gutachter: Prof. Dr. Marcin Pilipczuk Gutachter: Prof. Dr. Dimitrios Thilikos Tag der wissenschaftlichen Aussprache: 13. October 2017 Berlin 2017 2 This thesis is dedicated to my family, especially to my beautiful wife Atefe and my lovely son Shervin. 3 Contents Abstract iii Acknowledgementsv I. Introduction and Preliminaries1 1. Introduction2 1.0.1. General Techniques and Models......................3 1.1. Covering Problems.................................6 1.1.1. Covering Problems in Distributed Models: Case of Dominating Sets.6 1.1.2. Covering Problems in Directed Graphs: Finding Similar Patterns, the Case of Erd}os-P´osaproperty.......................9 1.2. Routing Problems in Directed Graphs...................... 11 1.2.1. Routing Problems............................. 11 1.2.2. Rerouting Problems............................ 12 1.3. Structure of the Thesis and Declaration of Authorship............. 14 2. Preliminaries and Notations 16 2.1. Basic Notations and Defnitions.......................... 16 2.1.1. Sets..................................... 16 2.1.2. Graphs................................... 16 2.2. Complexity Classes................................. 18 2.2.1. Approximation Algorithms........................ 18 2.2.2. Parametrized Complexity......................... 19 II. Covering Problems 21 3. Distributed Approximation Algorithms for Dominating Set 22 3.1. Introduction..................................... 22 3.2. Defnitions and General Lemmas......................... 23 3.3. The Local MDS Approximation......................... 26 3.3.1. Local MDS Approximation: Ideas and Proof Sketch......... 26 3.3.2. MDS Local Approximation Algorithm................. 28 3.3.3. Analysis................................... 29 3.4. O(g) Approximation Factor in O(g) Communication Rounds......... 33 3.5. (1 + δ)-Approximation for dominating set in H-Minor Free Graphs...... 35 3.5.1. Ideas and Proof Sketch.......................... 35 3.5.2. Proof Details................................ 36 i Contents 3.6. On Connected r-Dominating Set Problem ................ 38 3.7. Conclusion and Future Works........................... 41 4. On Dualities in Digraphs: Erd}os-P´osaproperty in Digraphs 42 4.1. Introduction..................................... 42 4.2. Directed Minors, Directed Grids and Directed Tree-Width........... 45 4.3. The Erd}os-P´osaproperty for Strongly Connected Digraphs.......... 50 4.4. The EP-Property for Vertex-Cyclic Digraphs.................. 52 4.5. Positive Instances for the Erd}os-P´osaProperty on Weakly Connected Digraphs 65 4.5.1. Strong Star................................. 66 4.5.2. Two Cycles Connected by a Single Edge................. 68 4.6. Conclusion and Future Work........................... 75 III. Routing and Connectivity Problems 76 5. On Disjoint Paths Problem in Digraphs 77 5.1. Introduction..................................... 77 5.2. Preliminaries.................................... 80 5.3. NP-Completeness of UpPlan-VDPP ...................... 81 5.4. A Linear Time Algorithm for UpPlan-VDPP for Fixed k ........... 86 5.5. Disjoint Paths With Congestion on DAGs.................... 90 5.6. Lower Bounds on Disjoint Paths with Congestion on DAGs.......... 93 5.7. Induced Path Problem............................... 93 5.8. Conclusion and Future Work........................... 97 6. Rerouting Problem 98 6.1. Introduction..................................... 98 6.2. Model and Defnitions............................... 98 6.3. Preliminaries.................................... 102 6.4. Congestion-Free Rerouting of Flows on DAGs.................. 103 6.5. NP-Hardness of 2-Flow Update in General Graphs............... 103 6.6. Optimal Solution for k = 2 Flows......................... 103 6.7. Updating k-Flows in DAGs is NP-complete................... 108 6.8. Linear Time Algorithm for Constant Number of Flows on DAGs....... 112 6.9. Conclusion and Future Work........................... 123 ii Abstract Structural graph theory proved itself a valuable tool for designing efcient algorithms for hard problems over recent decades. We exploit structural graph theory to provide novel techniques and algorithms for covering and connectivity problems. First, we focus on the Local model of distributed computing. In the Local model, minimizing the number of communication rounds is the main goal. We exploit the local properties of bounded genus graphs. We provide the frst constant factor approximation algorithm that solves the dominating set problem in constant rounds on bounded genus graphs. Then, we arbitrarily well approximate it in O(log∗ jGj) rounds. We also introduce a simple technique for graphs of bounded expansion which turns any constant factor approximation of r-dominating sets to a constant factor approximation of connected r-dominating sets. Finding similar patterns in graphs is one of the main challenges in graph theory. One such problem is either to fnd many disjoint instances of a particular pattern or to fnd a small set of vertices such that deleting them destroys all instances of that pattern. This question frst raised by Erd}osand P´osa.We provide an algorithmic classifcation for strongly connected digraphs analogous to the classical results of Robertson and Seymour on undirected graphs. Furthermore, a good characterization for vertex cyclic digraphs is provided. In the latter, we generalize Younger's conjecture to weakly connected digraphs. Next, we focus on routing and connectivity problems. The frst routing problem we consider is the Vertex Disjoint Paths Problem (VDPP) and its descendant problems. We provide an efcient algorithm for solving k-VDPP on upward planar digraphs in linear time for a fxed k. Then we allow the vertices to have some congestion and we solve the disjoint paths problem with congestion in acyclic digraphs. On the complexity side, we show the hardness of those problems when the corresponding parameter (e.g. k) is part of the input. It follows that the time complexity of our algorithms are almost optimal. We also show that induced path problem is hard even on digraphs of bounded directed tree-width. Finally, we consider the problem of rerouting. In a computer network, we may need to reroute packets from their old paths to new paths. The rerouting procedure should satisfy some consistency rules. E.g., the capacity of links should be respected, the fow of the packets cannot be interrupted, etc. Elements of the network are asynchronous. Thus, it is not possible to do the rerouting instantly. We show that it is NP-hard to fnd a feasible rerouting algorithm even on DAGs. In contrast, we provide a linear time rerouting algorithm on acyclic graphs for a fxed number of paths. iii Abstract Kurzfassung Die strukturelle Graphentheorie hat in den letzten Jahrzehnten einen wichtigen Beitrag zur Theorie der efzienten Graph-Algorithmen geleistet. Wir entwickeln weitere struk- turelle Ergebnisse und neue Techniken um Uberdeckungs-¨ und Zusammenhangsprobleme auf Graphen zu efzient zu l¨osen. Zun¨achst konzentrieren wir uns auf das Local Modell, das in verteilten Algorithmen Anwendung fndet. In diesem Modell geht es darum, die Kommunikation zwischen Klien- ten in einem Netzwerk zu minimieren, die ein globales Problem l¨osenm¨ochten. Wenn der Netzwerkgraph speziellen topologischen Einschr¨ankungen gen¨ugt,k¨onnenProbleme wesentlich schneller und besser gel¨ostwerden als in allgemeinen Graphen. Wir zeigen die Existenz einer constant-factor Approximation f¨urdas dominating set Problem, die in einer konstanten Zahl von Kommunikationsrunden im lokalen Modell ausgef¨uhrtwerden kann. Wir zeigen, dass in O(log∗ jGj) Runden sogar eine beliebig gute Approximation f¨urdas Problem berechnet werden kann. Weiterhin zeigen wir eine einfache Technik, mit Hilfe derer aus einem r-dominating set ein nur konstant gr¨oßeresverbundenes r-dominating set auf Graphen mit beschr¨ankterExpansion (bounded expansion) berechnet werden kann. Eine wichtige Anwendung der algorithmischen Graphentheorie ist die Suche nach gewissen Patterngraphen in einem großen Eingabegraphen. Eine wichtige Problemstellung ist es, eine kleine Zahl von Knoten zu fnden, so dass jedes Vorkommen eines festen Patterngraphen einen der gew¨ahltenKnoten enth¨alt.So sagt zum Beispiel der Satz von Erd}osand P´osa dass f¨urjede feste Zahl k eine Zahl f(k) existiert, so dass in jedem Graphen, der keine k knotendisjunkten Kreise enth¨alt,alle Kreise mit f(k) Knoten ¨uberdeckt werden k¨onnen.Ein entsprechender Dualit¨atssatzf¨urMinoren wurde von Robertson und Seymour gefunden. Wir beweisen einen analogen Charakterisierungssatz f¨urgerichtete Graphen. Weiterhin liefern wir einen Charakterisierungssatz f¨urgerichtete vertex cyclic Graphen. Mit diesem Satz verallgemeinern wir die Vermutung von Younger auf schwach zusammenh¨angendegerichtete Graphen. Im n¨achsten Teil der Arbeit konzentrieren wir uns auf Routing und Zusammenhangsprob- leme. Zun¨achst betrachten wir das Vertex Disjoint Paths Problem (VDPP) und verwandte Probleme. Wir liefern einen efzienten Algorithmus f¨urdas k-VDPP Problem auf upward planaren Graphen, dessen Laufzeit f¨urjedes feste k linear in der Eingabegr¨oßeist.
Load more

Recommended publications
  • Directed Graph Algorithms
    Directed Graph Algorithms CSE 373 Data Structures Readings • Reading Chapter 13 › Sections 13.3 and 13.4 Digraphs 2 Topological Sort 142 322 143 321 Problem: Find an order in which all these courses can 326 be taken. 370 341 Example: 142 Æ 143 Æ 378 Æ 370 Æ 321 Æ 341 Æ 322 Æ 326 Æ 421 Æ 401 378 421 In order to take a course, you must 401 take all of its prerequisites first Digraphs 3 Topological Sort Given a digraph G = (V, E), find a linear ordering of its vertices such that: for any edge (v, w) in E, v precedes w in the ordering B C A F D E Digraphs 4 Topo sort – valid solution B C Any linear ordering in which A all the arrows go to the right F is a valid solution D E A B F C D E Note that F can go anywhere in this list because it is not connected. Also the solution is not unique. Digraphs 5 Topo sort – invalid solution B C A Any linear ordering in which an arrow goes to the left F is not a valid solution D E A B F C E D NO! Digraphs 6 Paths and Cycles • Given a digraph G = (V,E), a path is a sequence of vertices v1,v2, …,vk such that: ›(vi,vi+1) in E for 1 < i < k › path length = number of edges in the path › path cost = sum of costs of each edge • A path is a cycle if : › k > 1; v1 = vk •G is acyclic if it has no cycles.
    [Show full text]
  • Graph Varieties Axiomatized by Semimedial, Medial, and Some Other Groupoid Identities
    Discussiones Mathematicae General Algebra and Applications 40 (2020) 143–157 doi:10.7151/dmgaa.1344 GRAPH VARIETIES AXIOMATIZED BY SEMIMEDIAL, MEDIAL, AND SOME OTHER GROUPOID IDENTITIES Erkko Lehtonen Technische Universit¨at Dresden Institut f¨ur Algebra 01062 Dresden, Germany e-mail: [email protected] and Chaowat Manyuen Department of Mathematics, Faculty of Science Khon Kaen University Khon Kaen 40002, Thailand e-mail: [email protected] Abstract Directed graphs without multiple edges can be represented as algebras of type (2, 0), so-called graph algebras. A graph is said to satisfy an identity if the corresponding graph algebra does, and the set of all graphs satisfying a set of identities is called a graph variety. We describe the graph varieties axiomatized by certain groupoid identities (medial, semimedial, autodis- tributive, commutative, idempotent, unipotent, zeropotent, alternative). Keywords: graph algebra, groupoid, identities, semimediality, mediality. 2010 Mathematics Subject Classification: 05C25, 03C05. 1. Introduction Graph algebras were introduced by Shallon [10] in 1979 with the purpose of providing examples of nonfinitely based finite algebras. Let us briefly recall this concept. Given a directed graph G = (V, E) without multiple edges, the graph algebra associated with G is the algebra A(G) = (V ∪ {∞}, ◦, ∞) of type (2, 0), 144 E. Lehtonen and C. Manyuen where ∞ is an element not belonging to V and the binary operation ◦ is defined by the rule u, if (u, v) ∈ E, u ◦ v := (∞, otherwise, for all u, v ∈ V ∪ {∞}. We will denote the product u ◦ v simply by juxtaposition uv. Using this representation, we may view any algebraic property of a graph algebra as a property of the graph with which it is associated.
    [Show full text]
  • Networkx: Network Analysis with Python
    NetworkX: Network Analysis with Python Salvatore Scellato Full tutorial presented at the XXX SunBelt Conference “NetworkX introduction: Hacking social networks using the Python programming language” by Aric Hagberg & Drew Conway Outline 1. Introduction to NetworkX 2. Getting started with Python and NetworkX 3. Basic network analysis 4. Writing your own code 5. You are ready for your project! 1. Introduction to NetworkX. Introduction to NetworkX - network analysis Vast amounts of network data are being generated and collected • Sociology: web pages, mobile phones, social networks • Technology: Internet routers, vehicular flows, power grids How can we analyze this networks? Introduction to NetworkX - Python awesomeness Introduction to NetworkX “Python package for the creation, manipulation and study of the structure, dynamics and functions of complex networks.” • Data structures for representing many types of networks, or graphs • Nodes can be any (hashable) Python object, edges can contain arbitrary data • Flexibility ideal for representing networks found in many different fields • Easy to install on multiple platforms • Online up-to-date documentation • First public release in April 2005 Introduction to NetworkX - design requirements • Tool to study the structure and dynamics of social, biological, and infrastructure networks • Ease-of-use and rapid development in a collaborative, multidisciplinary environment • Easy to learn, easy to teach • Open-source tool base that can easily grow in a multidisciplinary environment with non-expert users
    [Show full text]
  • Rounding Algorithms for Covering Problems
    Mathematical Programming 80 (1998) 63 89 Rounding algorithms for covering problems Dimitris Bertsimas a,,,1, Rakesh Vohra b,2 a Massachusetts Institute of Technology, Sloan School of Management, 50 Memorial Drive, Cambridge, MA 02142-1347, USA b Department of Management Science, Ohio State University, Ohio, USA Received 1 February 1994; received in revised form 1 January 1996 Abstract In the last 25 years approximation algorithms for discrete optimization problems have been in the center of research in the fields of mathematical programming and computer science. Re- cent results from computer science have identified barriers to the degree of approximability of discrete optimization problems unless P -- NP. As a result, as far as negative results are con- cerned a unifying picture is emerging. On the other hand, as far as particular approximation algorithms for different problems are concerned, the picture is not very clear. Different algo- rithms work for different problems and the insights gained from a successful analysis of a par- ticular problem rarely transfer to another. Our goal in this paper is to present a framework for the approximation of a class of integer programming problems (covering problems) through generic heuristics all based on rounding (deterministic using primal and dual information or randomized but with nonlinear rounding functions) of the optimal solution of a linear programming (LP) relaxation. We apply these generic heuristics to obtain in a systematic way many known as well as new results for the set covering, facility location, general covering, network design and cut covering problems. © 1998 The Mathematical Programming Society, Inc. Published by Elsevier Science B.V.
    [Show full text]
  • 7. NETWORK FLOW II ‣ Bipartite Matching ‣ Disjoint Paths
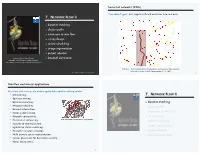
    Soviet rail network (1950s) "Free world" goal. Cut supplies (if cold war turns into real war). 7. NETWORK FLOW II ‣ bipartite matching ‣ disjoint paths ‣ extensions to max flow ‣ survey design ‣ airline scheduling ‣ image segmentation ‣ project selection Lecture slides by Kevin Wayne ‣ baseball elimination Copyright © 2005 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos Reference: On the history of the transportation and maximum flow problems. Alexander Schrijver in Math Programming, 91: 3, 2002. Last updated on Mar 31, 2013 3:25 PM Figure 2 2 From Harris and Ross [1955]: Schematic diagram of the railway network of the Western So- viet Union and Eastern European countries, with a maximum flow of value 163,000 tons from Russia to Eastern Europe, and a cut of capacity 163,000 tons indicated as ‘The bottleneck’. Max-flow and min-cut applications Max-flow and min-cut are widely applicable problem-solving model. ・Data mining. 7. NETWORK FLOW II ・Open-pit mining. ・Bipartite matching. ‣ bipartite matching ・Network reliability. ‣ disjoint paths ・Baseball elimination. ‣ extensions to max flow ・Image segmentation. ・Network connectivity. ‣ survey design liver and hepatic vascularization segmentation ・Distributed computing. ‣ airline scheduling ・Security of statistical data. ‣ image segmentation ・Egalitarian stable matching. ・Network intrusion detection. ‣ project selection ・Multi-camera scene reconstruction. ‣ baseball elimination ・Sensor placement for homeland security. ・Many, many, more. 3 Matching Bipartite matching Def. Given an undirected graph G = (V, E) a subset of edges M ⊆ E is Def. A graph G is bipartite if the nodes can be partitioned into two subsets a matching if each node appears in at most one edge in M.
    [Show full text]
  • Models for Networks with Consumable Resources: Applications to Smart Cities Hayato Montezuma Ushijima-Mwesigwa Clemson University, [email protected]
    Clemson University TigerPrints All Dissertations Dissertations 12-2018 Models for Networks with Consumable Resources: Applications to Smart Cities Hayato Montezuma Ushijima-Mwesigwa Clemson University, [email protected] Follow this and additional works at: https://tigerprints.clemson.edu/all_dissertations Recommended Citation Ushijima-Mwesigwa, Hayato Montezuma, "Models for Networks with Consumable Resources: Applications to Smart Cities" (2018). All Dissertations. 2284. https://tigerprints.clemson.edu/all_dissertations/2284 This Dissertation is brought to you for free and open access by the Dissertations at TigerPrints. It has been accepted for inclusion in All Dissertations by an authorized administrator of TigerPrints. For more information, please contact [email protected]. Models for Networks with Consumable Resources: Applications to Smart Cities A Dissertation Presented to the Graduate School of Clemson University In Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy Computer Science by Hayato Ushijima-Mwesigwa December 2018 Accepted by: Dr. Ilya Safro, Committee Chair Dr. Mashrur Chowdhury Dr. Brian Dean Dr. Feng Luo Abstract In this dissertation, we introduce different models for understanding and controlling the spreading dynamics of a network with a consumable resource. In particular, we consider a spreading process where a resource necessary for transit is partially consumed along the way while being refilled at special nodes on the network. Examples include fuel consumption of vehicles together with refueling stations, information loss during dissemination with error correcting nodes, consumption of ammunition of military troops while moving, and migration of wild animals in a network with a limited number of water-holes. We undertake this study from two different perspectives. First, we consider a network science perspective where we are interested in identifying the influential nodes, and estimating a nodes’ relative spreading influence in the network.
    [Show full text]
  • Katz Centrality for Directed Graphs • Understand How Katz Centrality Is an Extension of Eigenvector Centrality to Learning Directed Graphs
    Prof. Ralucca Gera, [email protected] Applied Mathematics Department, ExcellenceNaval Postgraduate Through Knowledge School MA4404 Complex Networks Katz Centrality for directed graphs • Understand how Katz centrality is an extension of Eigenvector Centrality to Learning directed graphs. Outcomes • Compute Katz centrality per node. • Interpret the meaning of the values of Katz centrality. Recall: Centralities Quality: what makes a node Mathematical Description Appropriate Usage Identification important (central) Lots of one-hop connections The number of vertices that Local influence Degree from influences directly matters deg Small diameter Lots of one-hop connections The proportion of the vertices Local influence Degree centrality from relative to the size of that influences directly matters deg C the graph Small diameter |V(G)| Lots of one-hop connections A weighted degree centrality For example when the Eigenvector centrality to high centrality vertices based on the weight of the people you are (recursive formula): neighbors (instead of a weight connected to matter. ∝ of 1 as in degree centrality) Recall: Strongly connected Definition: A directed graph D = (V, E) is strongly connected if and only if, for each pair of nodes u, v ∈ V, there is a path from u to v. • The Web graph is not strongly connected since • there are pairs of nodes u and v, there is no path from u to v and from v to u. • This presents a challenge for nodes that have an in‐degree of zero Add a link from each page to v every page and give each link a small transition probability controlled by a parameter β. u Source: http://en.wikipedia.org/wiki/Directed_acyclic_graph 4 Katz Centrality • Recall that the eigenvector centrality is a weighted degree obtained from the leading eigenvector of A: A x =λx , so its entries are 1 λ Thoughts on how to adapt the above formula for directed graphs? • Katz centrality: ∑ + β, Where β is a constant initial weight given to each vertex so that vertices with zero in degree (or out degree) are included in calculations.
    [Show full text]
  • A Gentle Introduction to Deep Learning for Graphs
    A Gentle Introduction to Deep Learning for Graphs Davide Bacciua, Federico Erricaa, Alessio Michelia, Marco Poddaa aDepartment of Computer Science, University of Pisa, Italy. Abstract The adaptive processing of graph data is a long-standing research topic that has been lately consolidated as a theme of major interest in the deep learning community. The snap increase in the amount and breadth of related research has come at the price of little systematization of knowledge and attention to earlier literature. This work is a tutorial introduction to the field of deep learn- ing for graphs. It favors a consistent and progressive presentation of the main concepts and architectural aspects over an exposition of the most recent liter- ature, for which the reader is referred to available surveys. The paper takes a top-down view of the problem, introducing a generalized formulation of graph representation learning based on a local and iterative approach to structured in- formation processing. Moreover, it introduces the basic building blocks that can be combined to design novel and effective neural models for graphs. We com- plement the methodological exposition with a discussion of interesting research challenges and applications in the field. Keywords: deep learning for graphs, graph neural networks, learning for structured data arXiv:1912.12693v2 [cs.LG] 15 Jun 2020 1. Introduction Graphs are a powerful tool to represent data that is produced by a variety of artificial and natural processes. A graph has a compositional nature, being a compound of atomic information pieces, and a relational nature, as the links defining its structure denote relationships between the linked entities.
    [Show full text]
  • 3.1 Matchings and Factors: Matchings and Covers
    1 3.1 Matchings and Factors: Matchings and Covers This copyrighted material is taken from Introduction to Graph Theory, 2nd Ed., by Doug West; and is not for further distribution beyond this course. These slides will be stored in a limited-access location on an IIT server and are not for distribution or use beyond Math 454/553. 2 Matchings 3.1.1 Definition A matching in a graph G is a set of non-loop edges with no shared endpoints. The vertices incident to the edges of a matching M are saturated by M (M-saturated); the others are unsaturated (M-unsaturated). A perfect matching in a graph is a matching that saturates every vertex. perfect matching M-unsaturated M-saturated M Contains copyrighted material from Introduction to Graph Theory by Doug West, 2nd Ed. Not for distribution beyond IIT’s Math 454/553. 3 Perfect Matchings in Complete Bipartite Graphs a 1 The perfect matchings in a complete b 2 X,Y-bigraph with |X|=|Y| exactly c 3 correspond to the bijections d 4 f: X -> Y e 5 Therefore Kn,n has n! perfect f 6 matchings. g 7 Kn,n The complete graph Kn has a perfect matching iff… Contains copyrighted material from Introduction to Graph Theory by Doug West, 2nd Ed. Not for distribution beyond IIT’s Math 454/553. 4 Perfect Matchings in Complete Graphs The complete graph Kn has a perfect matching iff n is even. So instead of Kn consider K2n. We count the perfect matchings in K2n by: (1) Selecting a vertex v (e.g., with the highest label) one choice u v (2) Selecting a vertex u to match to v K2n-2 2n-1 choices (3) Selecting a perfect matching on the rest of the vertices.
    [Show full text]
  • Graph Mining: Social Network Analysis and Information Diffusion
    Graph Mining: Social network analysis and Information Diffusion Davide Mottin, Konstantina Lazaridou Hasso Plattner Institute Graph Mining course Winter Semester 2016 Lecture road Introduction to social networks Real word networks’ characteristics Information diffusion GRAPH MINING WS 2016 2 Paper presentations ▪ Link to form: https://goo.gl/ivRhKO ▪ Choose the date(s) you are available ▪ Choose three papers according to preference (there are three lists) ▪ Choose at least one paper for each course part ▪ Register to the mailing list: https://lists.hpi.uni-potsdam.de/listinfo/graphmining-ws1617 GRAPH MINING WS 2016 3 What is a social network? ▪Oxford dictionary A social network is a network of social interactions and personal relationships GRAPH MINING WS 2016 4 What is an online social network? ▪ Oxford dictionary An online social network (OSN) is a dedicated website or other application, which enables users to communicate with each other by posting information, comments, messages, images, etc. ▪ Computer science : A network that consists of a finite number of users (nodes) that interact with each other (edges) by sharing information (labels, signs, edge directions etc.) GRAPH MINING WS 2016 5 Definitions ▪Vertex/Node : a user of the social network (Twitter user, an author in a co-authorship network, an actor etc.) ▪Edge/Link/Tie : the connection between two vertices referring to their relationship or interaction (friend-of relationship, re-tweeting activity, etc.) Graph G=(V,E) symbols meaning V users E connections deg(u) node degree:
    [Show full text]
  • Network Flow - Theory and Applications with Practical Impact
    3 Network flow - Theory and applications with practical impact Masao Iri Department of Information and System Engineering Faculty of Science and Engineering, Chuo University 1-13-27 Kasuga, Bunkyo-ku, Tokyo 112, Japan. Tel: +81-3-3817-1690. Fax: +81-3-3817-1681. e-mail: [email protected] Keywords Network flow, history, applications, duality, future 1 INTRODUCTION The research in this subject has now a long history and a large variety of related fields in science, engineering and operations research, and is still developing fast, especially in its algorithmic aspects, attracting many excellent senior as well as young researchers. And the space allotted to this paper is limited. So, in this paper I will not lay so much stress on particular frontiers of research in the subject as on the wider and historical viewpoint. Network-flow theory is one of the best studied and developed fields of optimization, and has important relations to quite different fields of science and technology such as com­ binatorial mathematics, algebraic topology, electric circuit theory, nonlinear continuum theory including plasticity theory, geographic information systems, VLSI design, etc., etc., besides standard applications to transportation, scheduling, etc. in operations research. An important point of view from which we should look at network flow theory is the "duality" viewpoint, to which due attention was paid at the earlier stages of development of the theory but which tends to be gradually ignored as time goes. Since the papers and books published on network flow are too many to cite here, I do not intend to compile even an incomplete list of references but only to cite a few which I directly mention and which I think tend to become obscured during the long history in spite of their ever lasting importance.
    [Show full text]
  • Inequity in Searching for Knowledge in Organizations
    The World is Not Small for Everyone: Inequity in Searching for Knowledge in Organizations _______________ Jasjit SINGH Morten HANSEN Joel PODOLNY 2010/11/ST/EFE (Revised version of 2009/49/ST/EFE) The World is Not Small for Everyone: Inequity in Searching for Knowledge in Organizations By Jasjit Singh * Morten T. Hansen** Joel M. Podolny*** ** February 2010 Revised version of INSEAD Working Paper 2009/49/ST/EFE * Assistant Professor of Strategy at INSEAD, 1 Ayer Rajah Avenue, Singapore 138676 Ph: +65 6799 5341 E-Mail: [email protected] ** Professor of Entrepreneurship at INSEAD, Boulevard de Constance, Fontainebleau 77305 France Ph: + 33 (0) 1 60 72 40 20 E-Mail: [email protected] *** Professor at Apple University, 1 Infinite Loop, MS 301-4AU, Cupertino, CA 95014, USA Email: [email protected] A working paper in the INSEAD Working Paper Series is intended as a means whereby a faculty researcher's thoughts and findings may be communicated to interested readers. The paper should be considered preliminary in nature and may require revision. Printed at INSEAD, Fontainebleau, France. Kindly do not reproduce or circulate without permission. ABSTRACT We explore why some employees may be at a disadvantage in searching for information in large complex organizations. The “small world” argument in social network theory emphasizes that people are on an average only a few connections away from the information they seek. However, we argue that such a network structure may benefit some people more than others. Specifically, some employees may have longer search paths in locating knowledge in an organization—their world may be large.
    [Show full text]