Possible Period of the Design of Nakshatras and Abhijit
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

An Innovative Model to Predict Earthquakes in Indian Peninsula Y
British Journal of Earth Sciences Research Vol.3, No.1, pp.42-62, September 2015 ___Published by European Centre for Research Training and Development UK (www.eajournals.org) AN INNOVATIVE MODEL TO PREDICT EARTHQUAKES IN INDIAN PENINSULA Y. V. Subba Rao Visiting Professor, Department of Jyotish Rashtriya Sanskrit University, Tirupati, A.P., India ABSTRACT: Can earthquakes be predicted? So far, the answer is no. Scientists are unlikely to be ever able to predict earthquakes with any amount of certainty, according to the United States Geological Survey Apr 25, 2013. An Innovative Model for Earthquake Prediction (IMEP) proposed in this paper is a combination of Vedic Astrology (Vedānga), Varāha Mihira’s Brihat Samhita and scientific data of magnetic variations, structural geology such as fault zones, tectonic plates’ directions, loose soil areas of all the earthquakes occurred in Indian Peninsula shield over a period of 200 years. In the course of preparation of this paper, it is observed that the earthquakes occured at regular intervals of about 11 years and mostly during bright fortnight due to extraordinary astronomical phenomena occurring in the planets and special movements of the heavenly bodies. Vedānga and Brihat Samhita state that earthquakes are caused by eclipses of the luminaries. It is, therefore, plausible to predict earthquakes in a specific locality within a specific time limit utilising this model. However, as an initial step, the present model has been designed for application for India. The next earthquake in Indian peninsula is predicted to occur on Wednesday, the 16th March, 2016 on the basis of the proposed hypothesis model. -

A-Level Physics a Question Paper Unit 05
Please write clearly in block capitals. Centre number Candidate number Surname –––––––––––––––––––––––––––––––––––––––––––––––––––––––––– Forename(s) –––––––––––––––––––––––––––––––––––––––––––––––––––––––––– Candidate signature –––––––––––––––––––––––––––––––––––––––––––––––––––––––––– A-level PHYSICS A Unit 5A Astrophysics Section B Tuesday 28 June 2016 Morning Time allowed: The total time for both sections of this paper is Materials For this paper you must have: 1 hour 45 minutes. You are a calculator advised to spend approximately a pencil and a ruler a Data and Formulae Booklet (enclosed). 50 minutes on this section. Instructions Use black ink or black ball-point pen. Fill in the boxes at the top of this page. Answer all questions. You must answer the questions in the spaces provided. Do not write outside the box around each page or on blank pages. Do all rough work in this book. Cross through any work you do not want to be marked. Show all your working. Information The marks for questions are shown in brackets. The maximum mark for this section is 35. You are expected to use a calculator where appropriate. A Data and Formulae Booklet is provided as a loose insert. You will be marked on your ability to: – use good English – organise information clearly – use specialist vocabulary where appropriate. (JUN16PHYA52A01) WMP/Jun16/E4 PHYA5/2A Do not write 2 outside the box Section B The maximum mark for this section is 35. You are advised to spend approximately 50 minutes on this section. 1 A converging lens of focal length 0.15 m is used as the eyepiece of an astronomical refracting telescope in normal adjustment. 1 (a) The angular magnification of the telescope is 5.0 Calculate the distance between the eyepiece lens and the objective lens of the telescope. -

The Atharvaveda and Its Paippalādaśākhā Arlo Griffiths, Annette Schmiedchen
The Atharvaveda and its Paippalādaśākhā Arlo Griffiths, Annette Schmiedchen To cite this version: Arlo Griffiths, Annette Schmiedchen. The Atharvaveda and its Paippalādaśākhā: Historical and philological papers on a Vedic tradition. Arlo Griffiths; Annette Schmiedchen. 11, Shaker, 2007, Indologica Halensis, 978-3-8322-6255-6. halshs-01929253 HAL Id: halshs-01929253 https://halshs.archives-ouvertes.fr/halshs-01929253 Submitted on 5 Dec 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Griffiths, Arlo, and Annette Schmiedchen, eds. 2007. The Atharvaveda and Its Paippalādaśākhā: Historical and Philological Papers on a Vedic Tradition. Indologica Halensis 11. Aachen: Shaker. Contents Arlo Griffiths Prefatory Remarks . III Philipp Kubisch The Metrical and Prosodical Structures of Books I–VII of the Vulgate Atharvavedasam. hita¯ .....................................................1 Alexander Lubotsky PS 8.15. Offense against a Brahmin . 23 Werner Knobl Zwei Studien zum Wortschatz der Paippalada-Sam¯ . hita¯ ..................35 Yasuhiro Tsuchiyama On the meaning of the word r¯as..tr´a: PS 10.4 . 71 Timothy Lubin The N¯ılarudropanis.ad and the Paippal¯adasam. hit¯a: A Critical Edition with Trans- lation of the Upanis.ad and Nar¯ ayan¯ . a’s D¯ıpik¯a ............................81 Arlo Griffiths The Ancillary Literature of the Paippalada¯ School: A Preliminary Survey with an Edition of the Caran. -

Modern-Baby-Names.Pdf
All about the best things on Hindu Names. BABY NAMES 2016 INDIAN HINDU BABY NAMES Share on Teweet on FACEBOOK TWITTER www.indianhindubaby.com Indian Hindu Baby Names 2016 www.indianhindubaby.com Table of Contents Baby boy names starting with A ............................................................................................................................... 4 Baby boy names starting with B ............................................................................................................................. 10 Baby boy names starting with C ............................................................................................................................. 12 Baby boy names starting with D ............................................................................................................................. 14 Baby boy names starting with E ............................................................................................................................. 18 Baby boy names starting with F .............................................................................................................................. 19 Baby boy names starting with G ............................................................................................................................. 19 Baby boy names starting with H ............................................................................................................................. 22 Baby boy names starting with I .............................................................................................................................. -

The Calendars of India
The Calendars of India By Vinod K. Mishra, Ph.D. 1 Preface. 4 1. Introduction 5 2. Basic Astronomy behind the Calendars 8 2.1 Different Kinds of Days 8 2.2 Different Kinds of Months 9 2.2.1 Synodic Month 9 2.2.2 Sidereal Month 11 2.2.3 Anomalistic Month 12 2.2.4 Draconic Month 13 2.2.5 Tropical Month 15 2.2.6 Other Lunar Periodicities 15 2.3 Different Kinds of Years 16 2.3.1 Lunar Year 17 2.3.2 Tropical Year 18 2.3.3 Siderial Year 19 2.3.4 Anomalistic Year 19 2.4 Precession of Equinoxes 19 2.5 Nutation 21 2.6 Planetary Motions 22 3. Types of Calendars 22 3.1 Lunar Calendar: Structure 23 3.2 Lunar Calendar: Example 24 3.3 Solar Calendar: Structure 26 3.4 Solar Calendar: Examples 27 3.4.1 Julian Calendar 27 3.4.2 Gregorian Calendar 28 3.4.3 Pre-Islamic Egyptian Calendar 30 3.4.4 Iranian Calendar 31 3.5 Lunisolar calendars: Structure 32 3.5.1 Method of Cycles 32 3.5.2 Improvements over Metonic Cycle 34 3.5.3 A Mathematical Model for Intercalation 34 3.5.3 Intercalation in India 35 3.6 Lunisolar Calendars: Examples 36 3.6.1 Chinese Lunisolar Year 36 3.6.2 Pre-Christian Greek Lunisolar Year 37 3.6.3 Jewish Lunisolar Year 38 3.7 Non-Astronomical Calendars 38 4. Indian Calendars 42 4.1 Traditional (Siderial Solar) 42 4.2 National Reformed (Tropical Solar) 49 4.3 The Nānakshāhī Calendar (Tropical Solar) 51 4.5 Traditional Lunisolar Year 52 4.5 Traditional Lunisolar Year (vaisnava) 58 5. -

Hasta Nakshatra ह�त न�� Hand of Kalapurush the Star of Knowledge, Action, Creativity and Determination
HASTA NAKSHATRA हत न HAND OF KALAPURUSH THE STAR OF KNOWLEDGE, ACTION, CREATIVITY AND DETERMINATION HASTA NAKSHATRA हत न 1 Page Notes prepared by Prof. Anthony Writer for thye students of Jyotisha Bharati, Bharatiya Vidya Bhavan, Mumbai, India HASTA NAKSHATRA हत न HAND OF KALAPURUSH THE STAR OF KNOWLEDGE, ACTION, CREATIVITY AND DETERMINATION Dennis Harness "The Nakshatras of Vedic Astrology: Ancient & Contemporary Usage" Hasta: The Hand (Virgo 10 00’ to 23 20’) The symbol for this nakshatra is the palm of the hand. The primary deity is Savitar, the Sun God, who promotes creativity. He is called “the golden handed one”. The shakti of Hasta is “the power to manifest what one seeks and place it in their hands”. Hasta natives can have great dexterity and are skilled with the healing arts, and with handicrafts. Hasta is ruled by the Moon, and in the sign of Virgo, ruled by Mercury, reflecting the very mental, intellectual nature of this lunar mansion. It has a deva temperament with a primary 2 motivation of moksha, or spiritual liberation. Page Notes prepared by Prof. Anthony Writer for thye students of Jyotisha Bharati, Bharatiya Vidya Bhavan, Mumbai, India HASTA NAKSHATRA हत न HAND OF KALAPURUSH THE STAR OF KNOWLEDGE, ACTION, CREATIVITY AND DETERMINATION 3 Page Notes prepared by Prof. Anthony Writer for thye students of Jyotisha Bharati, Bharatiya Vidya Bhavan, Mumbai, India HASTA NAKSHATRA हत न HAND OF KALAPURUSH THE STAR OF KNOWLEDGE, ACTION, CREATIVITY AND DETERMINATION Star of the clutching Hand Vedic Astrologers seek the blessings of the Sun God, as Savitar, for connecting us to the Divine Light, who is the supreme Lord of all consciousness behind all forms of light. -

Medicare Shared Savings Program
MEDICARE SHARED SAVINGS PROGRAM Accountable Care Organizations Participant Taxpayer Identification Numbers Names MSSP ACO Participant TIN Names for 2012 and 2013 As of August 2013 TABLE OF CONTENTS A.M. Beajow, M.D. Internal Medicine Associates ACO, P.C. ..................................................................... 9 AAMC Collaborative Care Network ........................................................................................................... 9 Accountable Care Clinical Services PC ...................................................................................................... 9 Accountable Care Coalition of Caldwell County, LLC .............................................................................. 11 Accountable Care Coalition of Central Georgia, LLC ............................................................................... 11 Accountable Care Coalition of Coastal Georgia, LLC ............................................................................... 12 Accountable Care Coalition of DeKalb, LLC ............................................................................................. 12 Accountable Care Coalition of Eastern North Carolina, LLC ................................................................... 14 Accountable Care Coalition of Georgia, LLC ........................................................................................... 15 Accountable Care Coalition of Greater Athens Georgia II, LLC ............................................................... 15 Accountable Care -

Possible Period of the Design of Naks Tras
1 Possible period of the design of Naks tras Sudha Bhujle 1 and M N Vahia 2 1 Raheja Vihar, Powai, Mumbai, [email protected] 2Tata Institute of Fundamental Research, Mumbai, [email protected] Sudha Bhujle and Mayank Vahia Abstract The Naks ¡ tras were designed to keep track of the moon’s path in the night sky. No literature gives the exact position of these Naks ¡ tras but there are many stories associated with each Nak s¡ tra. They were also probably used for time keeping over days. There are a total of 27 Nak s¡ tras spanning the night sky and the Moon spends an average of one day (night) in each Naks ¡ tra. However, as ¢ per the present association of stars with these Nak ¡ tras, several of them are as far as 25º away from the ecliptic where as Moon travels only about 5º on either side of the ecliptic. The possibility that in the remote past the ecliptic could have been 25º north to the present is not likely. We are not sure when the Naks ¡ tras were originally identified or when and how many times they were altered. To understand when could be the Naks ¡ tras defined. We studied the sky pattern from 3500 BC to 2005 AD and realized that the Moon path was closest to the maximum number of Naks ¡ tras around 3000 BC. We therefore suggest that the Naks ¡ tras were defined around 3000 BC and that the current association of star ¥ ¦ ¤ ¡ like. M£ga r with Naks tra needs to be re-examined Introduction 1 To appear in the Indian Journal of History of Science, 2006 The ancient Indian calendar dates back several thousand years and the relevant literature has been extensively collated in a major commentary called the Indian Calendar , by Sewell and Dikshit (1986). -
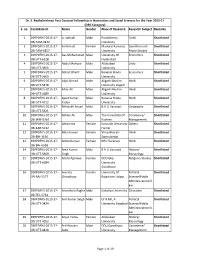
Dr. Radhakrishnan OBC.Xlsx
Dr. S. Radhakrishnan Post Doctoral Fellowship in Humanities and Social Sciences for the Year 2015-17 (OBC Category) S. no. Candidate ID Name Gender Place of Research Research Subject Remarks 1 DSRPDFHS-2015-17- A. Sathish Male Pondicherry Tamil Shortlisted OB-TAM-4432 University 2 DSRPDFHS-2015-17- A.Nirmala Female Madurai Kamaraj Gandhian and Shortlisted OB-TAM-6857 University Peace Studies 3 DSRPDFHS-2015-17- Aas Mohammad Male University Of Economics Shortlisted OB-UTT-6328 Hyderabad 4 DSRPDFHS-2015-17- Abdul Mohyee Male Allahabad Urdu Shortlisted OB-UTT-3656 University 5 DSRPDFHS-2015-17- Abhijit Bharti Male Banaras Hindu Economics Shortlisted OB-UTT-3605 University 6 DSRPDFHS-2015-17- Afjal Ahmad Male Aligarh Muslim Hindi Shortlisted OB-UTT-5478 University Aligarh 7 DSRPDFHS-2015-17- Afsar Ali Male Aligarh Muslim Hindi Shortlisted OB-UTT-4689 University 8 DSRPDFHS-2015-17- Ajeet Kumar Male Banaras Hindu Hindi Shortlisted OB-UTT-4712 Yadav University 9 DSRPDFHS-2015-17- Akhalakh Ansari Male B.H.U Varanasi Geography Shortlisted OB-UTT-5621 10 DSRPDFHS-2015-17- Akhter Ali Male The University Of Commerce/ Shortlisted OB-JAM-5367 Kashmir Management 11 DSRPDFHS-2015-17- Akkamma Female Kannada University Others Shortlisted OB-KAR-5132 Hampi 12 DSRPDFHS-2015-17- Akta Kumari Female Visva-Bharati- Hindi Shortlisted OB-BIH-3636 Santiniketan 13 DSRPDFHS-2015-17- Ambe Kumari Female BHU Varanasi Hindi Shortlisted OB-BIH-6538 14 DSRPDFHS-2015-17- Amit Kumar Male B H U Varanasi History/ Shortlisted OB-UTT-5668 Singh Museology 15 DSRPDFHS-2015-17- -

00E the Construction of the Universe Symphony
The basic construction of the Universe Symphony. There are 30 asterisms (Suites) in the Universe Symphony. I divided the asterisms into 15 groups. The asterisms in the same group, lay close to each other. Asterisms!! in Constellation!Stars!Objects nearby 01 The W!!!Cassiopeia!!Segin !!!!!!!Ruchbah !!!!!!!Marj !!!!!!!Schedar !!!!!!!Caph !!!!!!!!!Sailboat Cluster !!!!!!!!!Gamma Cassiopeia Nebula !!!!!!!!!NGC 129 !!!!!!!!!M 103 !!!!!!!!!NGC 637 !!!!!!!!!NGC 654 !!!!!!!!!NGC 659 !!!!!!!!!PacMan Nebula !!!!!!!!!Owl Cluster !!!!!!!!!NGC 663 Asterisms!! in Constellation!Stars!!Objects nearby 02 Northern Fly!!Aries!!!41 Arietis !!!!!!!39 Arietis!!! !!!!!!!35 Arietis !!!!!!!!!!NGC 1056 02 Whale’s Head!!Cetus!! ! Menkar !!!!!!!Lambda Ceti! !!!!!!!Mu Ceti !!!!!!!Xi2 Ceti !!!!!!!Kaffalijidhma !!!!!!!!!!IC 302 !!!!!!!!!!NGC 990 !!!!!!!!!!NGC 1024 !!!!!!!!!!NGC 1026 !!!!!!!!!!NGC 1070 !!!!!!!!!!NGC 1085 !!!!!!!!!!NGC 1107 !!!!!!!!!!NGC 1137 !!!!!!!!!!NGC 1143 !!!!!!!!!!NGC 1144 !!!!!!!!!!NGC 1153 Asterisms!! in Constellation Stars!!Objects nearby 03 Hyades!!!Taurus! Aldebaran !!!!!! Theta 2 Tauri !!!!!! Gamma Tauri !!!!!! Delta 1 Tauri !!!!!! Epsilon Tauri !!!!!!!!!Struve’s Lost Nebula !!!!!!!!!Hind’s Variable Nebula !!!!!!!!!IC 374 03 Kids!!!Auriga! Almaaz !!!!!! Hoedus II !!!!!! Hoedus I !!!!!!!!!The Kite Cluster !!!!!!!!!IC 397 03 Pleiades!! ! Taurus! Pleione (Seven Sisters)!! ! ! Atlas !!!!!! Alcyone !!!!!! Merope !!!!!! Electra !!!!!! Celaeno !!!!!! Taygeta !!!!!! Asterope !!!!!! Maia !!!!!!!!!Maia Nebula !!!!!!!!!Merope Nebula !!!!!!!!!Merope -

Five Shravana Mondays - Sri Rudrabhishekam Shravana Monday Rudrabhishekam for Lord Shiva’S Grace and Blessings
Five Shravana Mondays - Sri Rudrabhishekam Shravana Monday Rudrabhishekam for Lord Shiva’s grace and blessings Performing the Shravana Monday Pradosha Abhishekam to Lord Shiva, you will gain Lord Shiva’s blessings and reap the benefits in a timely manner. “Rajatha Bilvapatra Special Puja” (silver bael leaves puja) will also be performed. For those who perform abhishekam to Lord Shiva during this vratam on Shravana Monday evenings, you will be bestowed with money, grains, children, wife, relationship, happiness and wealth endlessly. This puja gives amazing results. According to ancient scriptures, for those who perform Pradosha Vratam on Shravana Mondays for 21 years, you will get the darshan of Lord Shiva Himself. Those who have not been able to perform this vratam for a long time should commence the vratam and perform it as long as possible. The month of Shravana begins on Sunday, August 8 with the first Monday puja beginning on Monday, August 9. 1. August 9th, Monday – for those in Ashlesha star, puja on this day will cure all doshas. 2. August 16th, Monday - Ashtami – for those in Anuradha star, puja on this day will bestow Akhanda (abundance) Aishwarya (wealth) Yoga to them. (Star on this day is Anuradha) 3. August 23rd, Monday - for those in Shatabhisha Star the homam and puja on this day bestows Mahadaishwarya (great wealth). 4. August 30th, Monday - Rohini Star - Kritika morning, Sri Mahalakshmi Yoga gives all good luck. Page 1 of 6 Five Shravana Tuesdays - Sri Mangala Gowri Devi Puja Sri Sugandha Kumkum and Silver Lotuses Puja When Sri Mangala Gowri Devi is worshiped on Shravana Tuesdays it is known as ‘Sarvaarthi Hara’; meaning all kinds of aarti (afflictions), anguish and distress will be removed. -

2005-01-Jan-Mar.Pdf
The Jyotish Digest Contents Volume I Issue 1. 2 Competition for Moon exploration Quarter Jan- Mar, 2005 Released Jan1, 2005 4 Jyotish to the rescue of farmers 4 Marriage prescriptions can be bothersome Editor Pt. Sanjay Rath 5 Politics and the Saëkaräcarya Editorial Editorial office 10 Your Letters SJC Puri, 212 Gopal Ballav Road, Puri 752001, India E-mail: 17 Kälacakra Daçä Narasimha Rao [email protected] 26 Kalachakra Dasa System Raman Suprajarama Consulting editors Brendan Feeley, Chandrasekhar 29 Timing in Relationships Phyllis Chubb Sharma, Narayan Iyer, P.V.R.Narasimha Rao, Pearl Finn, 38 War developments S. Prabhakaran Phyllis Chubb, Robert Koch, Sanjay 41 Timing Higher Education Hari Mahalingam Prabhakaran, Sarajit Poddar, Visti Larsen, Zoran Radosavljevic 49 Spiritual Teachings Cover 50 Timing marriage Chandrasekhar Sharma Dr. Pankaj Chande, Vice-Chancellor, Kavikulaguru Kalidas Sanskrit 57 Meditations University and Chandubhai Patel, noted Vedic astrologer at the SJC 58 Timing death Prabodh Venkhade Asia, Mumbai conference, 2005 65 Nakshatra Pada Lords Ramdas Rao Subscription & Membership Mihir Guha Roy 78 Timing Accidents Visti Larsen 15 B Gangaram Hospital Road, New Delhi, India 110060 E-mail: [email protected] ® Web pages Sri Jagannath Center (SJC) http://srijagannath.org/ Reg.No. S/45992/2003 under the Societies Registration Act (XXI) of 1860 jyotishdigest/ President: Sarbani Sarkar [email protected] Copyright Regd. Office: 15 B Gangaram Hospital Road, New Delhi 110060; Tel: 25717162 SJC India (W): J.K.Dasgupta,