Measurement of the Muon Lifetime
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

People and Things
sure that it is good for us to search though we could predict how every chaos. And of course it's even for them, in the same way that molecule in a glass of water would more true for sciences outside the Spanish explorers, whey they first behave, nowhere in the mountain area of physics, especially for pushed northward from the central of computer printout would we find sciences like astronomy and biolo parts of Mexico, were searching for the properties of water that really gy, for which also an element of the seven golden cities of Cibola. interest us, properties like tempera history enters. They didn't find them, but they ture and entropy. These properties I'm also not saying that elemen found other useful things, like have to be dealt with in their own tary particle physics is more impor Texas. terms, and for this we have the tant than other branches of phys Let me also say what I don't science of thermodynamics, which ics. All I'm saying is that, because mean by final, underlying, laws of deals with heat without at every of its concern with underlying laws, physics. I don't mean that other step reducing it to the properties of elementary particle physics has a branches of physics are in danger molecules or elementary particles. special importance of its own, even of being replaced by some ultimate There is no doubt today that, ul though it's not necessarily of great version of elementary particle timately, thermodynamics is what it immediate practical value. -
Character List
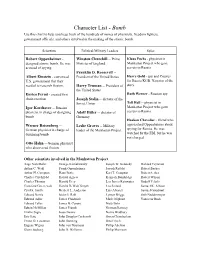
Character List - Bomb Use this chart to help you keep track of the hundreds of names of physicists, freedom fighters, government officials, and others involved in the making of the atomic bomb. Scientists Political/Military Leaders Spies Robert Oppenheimer - Winston Churchill -- Prime Klaus Fuchs - physicist in designed atomic bomb. He was Minister of England Manhattan Project who gave accused of spying. secrets to Russia Franklin D. Roosevelt -- Albert Einstein - convinced President of the United States Harry Gold - spy and Courier U.S. government that they for Russia KGB. Narrator of the needed to research fission. Harry Truman -- President of story the United States Enrico Fermi - created first Ruth Werner - Russian spy chain reaction Joseph Stalin -- dictator of the Tell Hall -- physicist in Soviet Union Igor Korchatov -- Russian Manhattan Project who gave physicist in charge of designing Adolf Hitler -- dictator of secrets to Russia bomb Germany Haakon Chevalier - friend who Werner Reisenberg -- Leslie Groves -- Military approached Oppenheimer about German physicist in charge of leader of the Manhattan Project spying for Russia. He was designing bomb watched by the FBI, but he was not charged. Otto Hahn -- German physicist who discovered fission Other scientists involved in the Manhattan Project: Aage Niels Bohr George Kistiakowsky Joseph W. Kennedy Richard Feynman Arthur C. Wahl Frank Oppenheimer Joseph Rotblat Robert Bacher Arthur H. Compton Hans Bethe Karl T. Compton Robert Serber Charles Critchfield Harold Agnew Kenneth Bainbridge Robert Wilson Charles Thomas Harold Urey Leo James Rainwater Rudolf Pelerls Crawford Greenewalt Harold DeWolf Smyth Leo Szilard Samuel K. Allison Cyril S. Smith Herbert L. Anderson Luis Alvarez Samuel Goudsmit Edward Norris Isidor I. -

Oral History Interview with Nicolas C. Metropolis
An Interview with NICOLAS C. METROPOLIS OH 135 Conducted by William Aspray on 29 May 1987 Los Alamos, NM Charles Babbage Institute The Center for the History of Information Processing University of Minnesota, Minneapolis Copyright, Charles Babbage Institute 1 Nicholas C. Metropolis Interview 29 May 1987 Abstract Metropolis, the first director of computing services at Los Alamos National Laboratory, discusses John von Neumann's work in computing. Most of the interview concerns activity at Los Alamos: how von Neumann came to consult at the laboratory; his scientific contacts there, including Metropolis, Robert Richtmyer, and Edward Teller; von Neumann's first hands-on experience with punched card equipment; his contributions to shock-fitting and the implosion problem; interactions between, and comparisons of von Neumann and Enrico Fermi; and the development of Monte Carlo techniques. Other topics include: the relationship between Turing and von Neumann; work on numerical methods for non-linear problems; and the ENIAC calculations done for Los Alamos. 2 NICHOLAS C. METROPOLIS INTERVIEW DATE: 29 May 1987 INTERVIEWER: William Aspray LOCATION: Los Alamos, NM ASPRAY: This is an interview on the 29th of May, 1987 in Los Alamos, New Mexico with Dr. Nicholas Metropolis. Why don't we begin by having you tell me something about when you first met von Neumann and what your relationship with him was over a period of time? METROPOLIS: Well, he first came to Los Alamos on the invitation of Dr. Oppenheimer. I don't remember quite when the date was that he came, but it was rather early on. It may have been the fall of 1943. -

Trinity Transcript
THE NATIONAL ACADEMIES Committee on International Security and Arms Control 60th Anniversary of Trinity: First Manmade Nuclear Explosion, July 16, 1945 PUBLIC SYMPOSIUM July 14, 2005 National Academy of Sciences Auditorium 2100 C Street, NW Washington, DC Proceedings By: CASET Associates, Ltd. 10201 Lee Highway, Suite 180 Fairfax, VA 22030 (703) 352-0091 CONTENTS PAGE Introductory Remarks Welcome: Ralph Cicerone, President, The National Academies (NAS) 1 Introduction: Raymond Jeanloz, Chair, Committee on International Security and Arms Control (CISAC) 3 Roundtable Discussion by Trinity Veterans Introduction: Wolfgang Panofsky, Chair 5 Individual Statements by Trinity Veterans: Harold Agnew 10 Hugh Bradner 13 Robert Christy 16 Val Fitch 20 Don Hornig 24 Lawrence Johnston 29 Arnold Kramish 31 Louis Rosen 35 Maurice Shapiro 38 Rubby Sherr 41 Harold Agnew (continued) 43 1 PROCEEDINGS 8:45 AM DR. JEANLOZ: My name is Raymond Jeanloz, and I am the Chair of the Committee on International Security and Arms Control that organized this morning’s symposium, recognizing the 60th anniversary of Trinity, the first manmade nuclear explosion. I will be the moderator for today’s event, and primarily will try to stay out of the way because we have many truly distinguished and notable speakers. In order to allow them the maximum amount of time, I will only give brief introductions and ask that you please turn to the biographical information that has been provided to you. To start with, it is my special honor to introduce Ralph Cicerone, the President of the National Academy of Sciences, who will open our meeting with introductory remarks. He is a distinguished researcher and scientific leader, recently serving as Chancellor of the University of California at Irvine, and his work in the area of climate change and pollution has had an important impact on policy. -

Magic of Muons: How a Magnet from the 90’S Could Usher in a New Age of Physics
Magic of Muons: How a magnet from the 90’s could usher in a new age of physics Joe Grange Argonne National Laboratory [email protected] To d ay ‣ Broad introduction to particle physics - what are we doing? why? ‣ The amazing muon as a tool for science and society ‣ History and future of “g-2” measurements - how an old magnet could revolutionize the field ‣ Wrapup 2 ‣ Broad introduction to particle physics - what are we doing? why? ‣ The amazing muon as a tool for science and society ‣ History and future of “g-2” measurements - how an old magnet could revolutionize the field ‣ Wrapup 3 Physics in a nutshell ‣ Broadly, here at Fermilab and around the 1 mm world we try to understand the world in terms of it’s most basic building blocks and how they interact 3x10-7 mm 1x10-7 mm 1x10-12 mm < 1x10-15 mm 4 Incredible richness in the sensory world arises from just a few particles ‣ Very small number of ingredients form everything you can see, feel or touch: p n e γ" 5 Amazing variety from such simple ingredients 6 Amazing variety from such simple ingredients 7 19th century hubris “In this field, almost everything is already p discovered, and all that remains is to fill a few unimportant holes.” (1878) Johann Philipp Gustav von Jolly advising Max Planck n not to pursue physics e 1918 γ" 8 Good thing Planck didn’t listen... ‣ His theory not only described never before seen phenomena, it revolutionized the fundamental description of the atom von Jolly was so happy with! ✓ 9 Since then.. -

Wave-Particle Duality
Wave-particle duality https://xkcd.com/967 History of the Standard Model, Part 2 July 8, 2020 1 Fundamental Forces https://xkcd.com/1489 History of the Standard Model, Part 2 July 8, 2020 2 QuarkNet Summer Session for Teachers: The Standard Model and Beyond Allie Reinsvold Hall https://quarknet.org/content/quarknet-summer- session-teachers-2020 Summer 2020 History of the Standard Model, Part 2 July 8, 2020 3 Course overview What are the fundamental building blocks that make up our universe? Mission: overview of the past, present, and future of particle physics 1. History of the Standard Model, Part 1: Ancient Greeks to Quantum Mechanics 2. History of the Standard Model, Part 2: Particle zoo and the Standard Model 3. Particle physics at the Large Hadron Collider (LHC) 4. Beyond the Standard Model at the LHC 5. Neutrino physics 6. Dark matter and cosmology Goal: Bring you to whatever your next level of understanding is and provide resources for when you teach. Not everyone is at the same level and that’s okay. History of the Standard Model, Part 2 July 8, 2020 4 Loose ends from last week • Lost Discoveries by Dick Teresi • Derivation of the energy and time relationship in Heisenberg’s uncertainty principle: https://quarknet.org/content/note- consistency-complimentary-variables https://quarknet.org/sites/default/fil es/Heisenberg%20and%20Diffraction. pdf https://quarknet.org/sites/default/fil es/Heisenberg%20and%20Energy.pdf • Fill out the weekly report if you haven’t already done so! • Everyone so far agreed to share their contact info – thanks! History of the Standard Model, Part 2 July 8, 2020 5 Loose ends from last week Excellent question on the weekly survey: “How can we help students understand the connection between particles and waves that is required in the quantum world?” You all are better equipped to answer that than I am – time for breakout discussions! Introduce yourself to today’s group. -

An Atomic History Chapter 2
An Atomic History 0-3 8/11/02 7:31 AM Page 18 Chapter Two 19 THE FERMI-SZILARD PILE AND URANIUM RESEARCH The first government funding for nuclear research was allocated to purchase graphite and uranium oxide for the chain reaction experiments being organized by Fermi and World War II and the Manhattan Project Szilard at Columbia University in February 1940.2 This work, which began in New York 2 City, soon spread to Princeton, the University of Chicago, and research institutions in California.3 Even at this stage, the scientists knew that a chain reaction would need three major components in the right combination: fuel, moderator, and coolant. The fuel would contain the fissile material needed to support the fission process. The neutrons generated by the fission process had to be slowed by the moderator so that they could initiate addi- tional fission reactions. The heat that resulted from this process had to be removed by the coolant. Fermi’s initial research explored the possibility of a chain reaction with natural urani- The 1930s were a time of rapid progress in the development of nuclear physics. um. It was quickly determined that high-purity graphite served as the best neutron moder- Research accelerated in the early years of the Second World War, when new developments ator out of the materials then available.4 After extensive tests throughout 1940 and early were conceived and implemented in the midst of increasing wartime urgency. American 1941, Fermi and Szilard set up the first blocks of graphite at Columbia University in government interest in these developments was limited at first, but increased as the war September 1941. -

A Nature of Science Guided Approach to the Physics Teaching of Cosmic Rays
A Nature of Science guided approach to the physics teaching of Cosmic Rays Dissertation zur Erlangung des akademischen Grades Doktorin der Philosophie (Dr. phil. { Doctor philosophiae) eingereicht am Fachbereich 4 Mathematik, Naturwissenschaften, Wirtschaft & Informatik der Universit¨atHildesheim vorgelegt von Rosalia Madonia geboren am 20. August 1961 in Palermo 2018 Schwerpunkt der Arbeit: Didaktik der Physik Tag der Disputation: 21 Januar 2019 Dekan: Prof. Dr. M. Sauerwein 1. Gutachter: Prof. Dr. Ute Kraus 2. Gutachter: Prof. Dr. Peter Grabmayr ii Abstract This thesis focuses on cosmic rays and Nature of Science (NOS). The first aim of this work is to investigate whether the variegated aspects of cosmic ray research -from its historical development to the science topics addressed herein- can be used for a teaching approach with and about NOS. The efficacy of the NOS based teaching has been highlighted in many studies, aimed at developing innovative and more effective teaching strategies. The fil rouge that we propose unwinds through cosmic ray research, that with its century long history appears to be the perfect topic for a study of and through NOS. The second aim of the work is to find out what knowledge the pupils and students have regarding the many aspect of NOS. To this end we have designed, executed, and analyzed the outcomes of a sample-based investigation carried out with pupils and students in Palermo (Italy), T¨ubingenand Hildesheim (Germany), and constructed around an open-ended ques- tionnaire. The main goal is to study whether intrinsic differences between the German and Italian samples can be observed. The thesis is divided in three parts. -

Carl David Anderson Biographical Memoir
NATIONAL ACADEMY OF SCIENCES C A R L D A V I D A NDERSON 1905—1991 A Biographical Memoir by WILLIAM H. PICKERING Any opinions expressed in this memoir are those of the author(s) and do not necessarily reflect the views of the National Academy of Sciences. Biographical Memoir COPYRIGHT 1998 NATIONAL ACADEMIES PRESS WASHINGTON D.C. CourtesyofInstituteArchives,CaliforniaInstituteofTechnology,Pasadena CARLDAVIDANDERSON September3,1905–January11,1991 BYWILLIAMH.PICKERING ESTKNOWNFORHISdiscoveryofthepositiveelectron, Borpositron,CarlDavidAndersonwasawardedthe NobelPrizeinphysicsin1936atagethirty-one.Thedis- coveryofthepositronwasthefirstofthenewparticlesof modernphysics.Electronsandprotonshadbeenknown andexperimentedwithforaboutfortyyears,anditwas assumedthatthesewerethebuildingblocksofallmatter. Withthediscoveryofthepositron,anexampleofanti- matter,allmanneroftheoreticalandexperimentalpossi- bilitiesarose.TheRoyalSocietyofLondoncalledCarl’s discovery“oneofthemostmomentousofthecentury.” BornonSeptember3,1905,inNewYorkCity,Carlwas theonlysonofSwedishimmigrantparents.Hisfather,the seniorCarlDavidAnderson,hadbeenintheUnitedStates since1896.WhenCarlwassevenyearsold,thefamilyleft NewYorkforLosAngeles,whereCarlattendedpublic schoolsandin1923enteredtheCaliforniaInstituteof Technology.Caltechhadopeneditsdoorsin1921with RobertA.Millikan,himselfaNobellaureate,aschiefex- ecutive.TogetherwithchemistArthurA.Noyesandas- tronomerGeorgeElleryHale,Millikanestablishedthehigh standardofexcellenceandthesmallstudentbodythat todaycontinuestocharacterizeCaltech. -

Lecture 10 Fall 2018 Semester Prof
Physics 56400 Introduction to Elementary Particle Physics I Lecture 10 Fall 2018 Semester Prof. Matthew Jones Elementary Particles • Atomic physics: – Proton, neutron, electron, photon • Nuclear physics: – Alpha, beta, gamma rays • Cosmic rays: – Something charged (but what?) • Relativistic quantum mechanics (Dirac, 1928) – Some solutions described electrons (with positive energy) – Other solutions described electrons with negative energy – Dirac came up with an elegant explanation for to think about this… The Dirac Sea • Dirac proposed that all electrons have negative charge. • Normal electrons have positive energy. • All negative-energy states are populated and form the Dirac sea. • The Pauli exclusion principle explains why positive- energy electrons can’t reach a lower energy state – those states are already populated • The only way to observe an electron in the sea would be to give it a positive energy. The Dirac Sea Energy Lowest positive-energy +푚푒 state corresponds to an electron at rest. It can’t fall into the sea −푚푒 because those states are already filled. The Dirac Sea Energy Now we have a positive energy electron, and a hole in the sea. +푚푒 The absence of a negative charge looks −푚푒 like a positive charge. This describes pair production. The Dirac Sea Energy Now that there is a hole in the sea, a positive energy electron can fall +푚푒 into it, releasing energy. −푚푒 This corresponds to electron-positron annihilation. Positrons • This explanation was not immediately interpreted as a prediction for a new particle • However, Carl Anderson observed “positive electrons” in cosmic rays in 1933. • Nobel prize in 1934. • Anti-particles are a natural consequence of special relativity and quantum mechanics. -

Character List
Character List - Bomb Use this chart to help you keep track of the hundreds of names of physicists, freedom fighters, government officials, and others involved in the making of the atomic bomb. Scientists Political/Military Leaders Spies Robert Oppenheimer - Winston Churchill -- Prime Klaus Fuchs - physicist in designed atomic bomb. He was Minister of England Manhattan Project who gave accused of spying. secrets to Russia Franklin D. Roosevelt -- Albert Einstein - convinced President of the United States Harry Gold - spy and Courier U.S. government that they for Russia KGB. Narrator of the needed to research fission. Harry Truman -- President of story the United States Enrico Fermi - created first Ruth Werner - Russian spy chain reaction Joseph Stalin -- dictator of the Tell Hall -- physicist in Soviet Union Igor Korchatov -- Russian Manhattan Project who gave physicist in charge of designing Adolf Hitler -- dictator of secrets to Russia bomb Germany Haakon Chevalier - friend who Werner Reisenberg -- Leslie Groves -- Military approached Oppenheimer about German physicist in charge of leader of the Manhattan Project spying for Russia. He was designing bomb watched by the FBI, but he was not charged. Otto Hahn -- German physicist who discovered fission Other scientists involved in the Manhattan Project: Aage Niels Bohr George Kistiakowsky Joseph W. Kennedy Richard Feynman Arthur C. Wahl Frank Oppenheimer Joseph Rotblat Robert Bacher Arthur H. Compton Hans Bethe Karl T. Compton Robert Serber Charles Critchfield Harold Agnew Kenneth Bainbridge Robert Wilson Charles Thomas Harold Urey Leo James Rainwater Rudolf Pelerls Crawford Greenewalt Harold DeWolf Smyth Leo Szilard Samuel K. Allison Cyril S. Smith Herbert L. Anderson Luis Alvarez Samuel Goudsmit Edward Norris Isidor I. -

The Particle Odyssey
One Century of Cosmic Rays A particle physicist’s view Christine Sutton CERN SUGAR 2015 Christine Sutton 1 A particle physicist’s view Pre-history: Common roots in the 19th century Discovery: Adventures in the early 20th century What are they? Discoveries up to ~1950 Neutrino astronomy: A new view of the cosmos Gamma-ray astronomy: A new way to view of the cosmos …with interludes from particle physics SUGAR 2015 Christine Sutton 2 There are more things in heaven and earth than are dreamt of in your philosophy … William Shakespeare (Hamlet) SUGAR 2015 Christine Sutton 3 1785 Charles de Coulomb discovers the spontaneous discharge of isolated electrified bodies 1834 Michael Faraday makes further investigations; he introduces the term ‘ion’ 1879 William Crookes discovers the speed of discharge decreases when the pressure is reduced → ionization of air SUGAR 2015 Christine Sutton 4 1895 Charles Wilson invents the cloud chamber 1895 Wilhem Röntgen discovers x-rays while investigating cathode rays in a ‘Crookes’ tube 1896 Henri Becquerel discovers radioactivity while investigating the production of x-rays 1897 J J Thomson discovers that cathode rays consist of particles much smaller than the atom → the electron SUGAR 2015 Christine Sutton 5 1899 Ernest Rutherford discovers two forms of radioactivity: α and β 1900 Philippe Villard discovers a third, penetrating type of radioactivity, named γ rays by Rutherford ~1900 Wilson in Scotland, and Julius Elster and Hans Geitelin in Germany improve the insulation of electroscopes and hence the sensitivity