DOCSLIB.ORG

Geoide Ssii-109

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Geoide Ssii-109 GEOIDE SSII-109 MAP DISTORTIONS MAP DISTORTION • No map projection maintains correct scale throughout • The intersection of any two lines on the Earth is represented on the map at the same or different angle • Map projections aim to either minimize scale, angular or area distortion TISSOT'S THEOREM At every point there are two orthogonal principal directions which are perpendicular on both the Earth (u) and the map (u') Figure (A) displays a point on the Earth and (B) a point on the projection TISSOT'S INDICATRIX • An infinitely small circle on the Earth will project as an infinitely small ellipse on any map projection (except conformal projections where it is a circle) • Major and minor axis of ellipse are directly related to the scale distortion and the maximum angular deformation SCALE DISTORTION • The ratio of an infinitesimal linear distance in any direction at any point on the projection and the corresponding infinitesimal linear distance on the Earth • h – scale distortion along the meridians • k – scale distortion along the parallels MAXIMUM ANGULAR DEFORMATION AND AREAL SCALE FACTOR • Maximum angular deformation, w is the biggest deviation from principle directions define on the Earth to the principle directions define on the map • Occurs in each of the four quadrants define by the principle directions of Tissot's indicatrix • Areal scale factor is the exaggeration of an infinitesimally small area at a particular point NOTES • Three tangent points are taken for a number of different azimuthal projection: (φ, λ)= (0°, 0°), (φ, λ)= (45° N, 0°), (φ, λ)= (80° N, 0°) • Each projection covers a ‘square’ on the Earth, with latitude and longitude increasing in increments of 1° • Ellipsoidal (WGS84) equations are used for the projections AZIMUTHAL PROJECTIONS • Direction or azimuth from the centre of the projection to every other point on the map is show correctly • Scale and distortions change only with the distance from the centre • One standard point (centre of projection) LAMBERT AZIMUTHAL EQUAL AREA • Equal area • Central meridian is a straight line on all aspects • All other meridians and parallels are complex curves • Not a perspective projection • Scale increases radially as the distance increases from the tangent point • Scale increases in the direction perpendicular to radii as the distance increases from the tangent point LAMBERT AZIMUTHAL EQUAL AREA Scale Distortion Along Meridians (h) Scale Distortion Along Parallels (k) Longitude (°) Longitude (°) Latitude (°) 2 W 1 W 0 1 E 2 E Latitude (°) 2 W 1 W 0 1 E 2 E 2 N 1.0000 0.9999 0.9998 0.9999 1.0000 2 N 1.0000 1.0001 1.0002 1.0001 1.0000 1 N 1.0001 1.0000 1.0000 1.0000 1.0001 1 N 0.9999 1.0000 1.0000 1.0000 0.9999 0 1.0002 1.0000 1.0000 1.0000 1.0002 0 0.9998 1.0000 1.0000 1.0000 0.9998 1 S 1.0001 1.0000 1.0000 1.0000 1.0001 1 S 0.9999 1.0000 1.0000 1.0000 0.9999 2 S 1.0000 0.9999 0.9998 0.9999 1.0000 2 S 1.0000 1.0001 1.0002 1.0001 1.0000 Longitude (°) Longitude (°) Latitude (°) 2 W 1 W 0 1 E 2 E Latitude (°) 2 W 1 W 0 1 E 2 E 47 N 0.9999 0.9998 0.9998 0.9998 0.9999 47 N 1.0001 1.0002 1.0002 1.0002 1.0001 46 N 1.0000 1.0000 0.9999 1.0000 1.0000 46 N 1.0000 1.0000 1.0001 1.0000 1.0000 45 N 1.0001 1.0000 1.0000 1.0000 1.0001 45 N 0.9999 1.0000 1.0000 1.0000 0.9999 44 N 1.0001 1.0000 1.0000 1.0000 1.0001 44 N 0.9999 1.0000 1.0000 1.0000 0.9999 43 N 1.0000 0.9999 0.9999 0.9999 1.0000 43 N 1.0000 1.0001 1.0001 1.0001 1.0000 Longitude (°) Longitude (°) Latitude (°) 2 W 1 W 0 1 E 2 E Latitude (°) 2 W 1 W 0 1 E 2 E 82 N 0.9998 0.9998 0.9998 0.9998 0.9998 82 N 1.0002 1.0002 1.0002 1.0002 1.0002 81 N 1.0000 1.0000 1.0000 1.0000 1.0000 81 N 1.0000 1.0000 1.0000 1.0000 1.0000 80 N 1.0000 1.0000 1.0000 1.0000 1.0000 80 N 1.0000 1.0000 1.0000 1.0000 1.0000 79 N 1.0000 1.0000 1.0000 1.0000 1.0000 79 N 1.0000 1.0000 1.0000 1.0000 1.0000 78 N 0.9999 0.9999 0.9999 0.9999 0.9999 78 N 1.0001 1.0001 1.0001 1.0001 1.0001 LAMBERT AZIMUTHAL EQUAL AREA Angular Deformation (w) Longitude (°) Latitude (°) 2 W 1 W 0 1 E 2 E 2 N 2' 5.65'' 1' 18.54'' 1' 2.83'' 1' 18.54'' 2' 5.65'' 1 N 1' 18.54'' 31.41'' 15.71'' 31.41'' 1' 18.54'' 0 1' 2.84'' 15.71'' 0 15.71'' 1' 2.84'' 1 S 1' 18.54'' 31.41'' 15.71'' 31.41'' 1' 18.54'' 2 S 2' 5.65'' 1' 18.54'' 1' 2.83'' 1' 18.54'' 2' 5.65'' Longitude (°) Latitude (°) 2 W 1 W 0 1 E 2 E 47 N 1' 49.95'' 1' 26.74'' 1' 18.95'' 1' 26.74'' 1' 49.95'' 46 N 55.90'' 32.01'' 23.76'' 32.01'' 55.90'' 45 N 33.55'' 9.73'' 0 9.73'' 33.55'' 44 N 41.41'' 16.71'' 7.65'' 16.71'' 41.41'' 43 N 1' 20.23'' 55.20'' 46.72'' 55.20'' 1' 20.23'' Longitude (°) Latitude (°) 2 W 1 W 0 1 E 2 E 82 N 1' 9.91'' 1' 8.76'' 1' 8.37'' 1' 8.76'' 1' 49.95'' 81 N 20.22'' 18.91'' 18.48'' 18.91'' 55.90'' 80 N 2.14'' 0.68'' 0 0.68'' 33.55'' 79 N 15.08'' 13.48'' 12.94'' 13.48'' 41.41'' 78 N 59.60'' 57.87'' 57.30'' 57.87'' 1' 20.23'' LAMBERT AZIMUTHAL EQUAL AREA TISSOT’S INDICATRICES If |a – b| < 0.001 ellipse is shown in green colour otherwise it is red Tangent Point: (φ, λ)= (0°, 0°) LAMBERT AZIMUTHAL EQUAL AREA TISSOT’S INDICATRICES If |a – b| < 0.001 ellipse is shown in green colour otherwise it is red Tangent Point: (φ, λ)= (45° N, 0°) LAMBERT AZIMUTHAL EQUAL AREA TISSOT’S INDICATRICES If |a – b| < 0.001 ellipse is shown in green colour otherwise it is red Tangent Point: (φ, λ)= (80° N, 0°) LAMBERT AZIMUTHAL EQUAL AREA TISSOT’S INDICATRICES Semi major - axis (a) Longitude (°) Latitude (°) 5 W 4 W 3 W 2 W 1 W 0 1 E 2 E 3 E 4 E 5 E 5N 1.0019 1.0016 1.0013 1.0011 1.0010 1.0010 1.0010 1.0011 1.0013 1.0016 1.0019 4 N 1.0016 1.0012 1.0010 1.0008 1.0006 1.0006 1.0006 1.0008 1.0010 1.0012 1.0016 3 N 1.0013 1.0010 1.0007 1.0005 1.0004 1.0003 1.0004 1.0005 1.0007 1.0010 1.0013 2 N 1.0011 1.0008 1.0005 1.0003 1.0002 1.0002 1.0002 1.0003 1.0005 1.0008 1.0011 1 N 1.0010 1.0006 1.0004 1.0002 1.0001 1.0000 1.0001 1.0002 1.0004 1.0006 1.0010 0 1.0010 1.0006 1.0003 1.0002 1.0000 1.0000 1.0000 1.0002 1.0003 1.0006 1.0010 1 S 1.0010 1.0006 1.0004 1.0002 1.0001 1.0000 1.0001 1.0002 1.0004 1.0006 1.0010 2 S 1.0011 1.0008 1.0005 1.0003 1.0002 1.0002 1.0002 1.0003 1.0005 1.0008 1.0011 3 S 1.0013 1.0010 1.0007 1.0005 1.0004 1.0003 1.0004 1.0005 1.0007 1.0010 1.0013 4S 1.0016 1.0012 1.0010 1.0008 1.0006 1.0006 1.0006 1.0008 1.0010 1.0012 1.0016 5 S 1.0019 1.0016 1.0013 1.0011 1.0010 1.0010 1.0010 1.0011 1.0013 1.0016 1.0019 Longitude (°) Latitude (°) 5 W 4 W 3 W 2 W 1 W 0 1 E 2 E 3 E 4 E 5 E 50 N 1.0015 1.0013 1.0012 1.0011 1.0011 1.0011 1.0011 1.0011 1.0012 1.0013 1.0015 49 N 1.0011 1.0010 1.0008 1.0008 1.0007 1.0007 1.0007 1.0008 1.0008 1.0010 1.0011 48 N 1.0009 1.0007 1.0006 1.0005 1.0004 1.0004 1.0004 1.0005 1.0006 1.0007 1.0009 47 N 1.0007 1.0005 1.0004 1.0003 1.0002 1.0002 1.0002 1.0003 1.0004 1.0005 1.0007 46 N 1.0005 1.0004 1.0002 1.0001 1.0001 1.0001 1.0001 1.0001 1.0002 1.0004 1.0005 45 N 1.0005 1.0003 1.0002 1.0001 1.0000 1.0000 1.0000 1.0001 1.0002 1.0003 1.0005 44 N 1.0005 1.0003 1.0002 1.0001 1.0000 1.0000 1.0000 1.0001 1.0002 1.0003 1.0005 43 N 1.0006 1.0004 1.0003 1.0002 1.0001 1.0001 1.0001 1.0002 1.0003 1.0004 1.0006 42 N 1.0008 1.0006 1.0005 1.0004 1.0003 1.0003 1.0003 1.0004 1.0005 1.0006 1.0008 41 N 1.0010 1.0009 1.0007 1.0006 1.0006 1.0005 1.0006 1.0006 1.0007 1.0009 1.0010 40 N 1.0014 1.0012 1.0010 1.0009 1.0009 1.0009 1.0009 1.0009 1.0010 1.0012 1.0014 Longitude (°) Latitude (°) 5 W 4 W 3 W 2 W 1 W 0 1 E 2 E 3 E 4 E 5 E 85N 1.0010 1.0010 1.0010 1.0010 1.0010 1.0010 1.0010 1.0010 1.0010 1.0010 1.0010 84 N 1.0007 1.0006 1.0006 1.0006 1.0006 1.0006 1.0006 1.0006 1.0006 1.0006 1.0007 83 N 1.0004 1.0004 1.0004 1.0004 1.0004 1.0004 1.0004 1.0004 1.0004 1.0004 1.0004 82 N 1.0002 1.0002 1.0002 1.0002 1.0002 1.0002 1.0002 1.0002 1.0002 1.0002 1.0002 81 N 1.0001 1.0001 1.0001 1.0000 1.0000 1.0000 1.0000 1.0000 1.0001 1.0001 1.0001 80 N 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 79 N 1.0001 1.0001 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0001 1.0001 78 N 1.0002 1.0002 1.0002 1.0001 1.0001 1.0001 1.0001 1.0001 1.0002 1.0002 1.0002 77 N 1.0004 1.0003 1.0003 1.0003 1.0003 1.0003 1.0003 1.0003 1.0003 1.0003 1.0004 76 N 1.0006 1.0006 1.0006 1.0006 1.0006 1.0006 1.0006 1.0006 1.0006 1.0006 1.0006 75 N 1.0010 1.0009 1.0009 1.0009 1.0009 1.0009 1.0009 1.0009 1.0009 1.0009 1.0010 LAMBERT AZIMUTHAL EQUAL AREA TISSOT’S INDICATRICES Semi minor - axis (b) Longitude (°) Latitude (°) 5 W 4 W 3 W 2 W 1 W 0 1 E 2 E 3 E 4 E 5 E 5N 0.9981 0.9984 0.9987 0.9989 0.9990 0.9990 0.9990 0.9989 0.9987 0.9984 0.9981 4 N 0.9984 0.9988 0.9990 0.9992 0.9994 0.9994 0.9994 0.9992 0.9990 0.9988 0.9984 3 N 0.9987 0.9990 0.9993 0.9995 0.9996 0.9997 0.9996 0.9995 0.9993 0.9990 0.9987 2 N 0.9989 0.9992 0.9995 0.9997 0.9998 0.9998 0.9998 0.9997 0.9995 0.9992 0.9989 1 N 0.9990 0.9994 0.9996 0.9998 0.9999 1.0000 0.9999 0.9998 0.9996 0.9994 0.9990 0 0.9990 0.9994 0.9997 0.9998 1.0000 1.0000 1.0000 0.9998 0.9997 0.9994 0.9990 1 S 0.9990 0.9994 0.9996 0.9998 0.9999 1.0000 0.9999 0.9998 0.9996 0.9994 0.9990 2 S 0.9989 0.9992 0.9995 0.9997 0.9998 0.9998 0.9998 0.9997 0.9995 0.9992 0.9989 3 S 0.9987 0.9990 0.9993 0.9995 0.9996 0.9997 0.9996 0.9995 0.9993 0.9990 0.9987 4S 0.9984 0.9988 0.9990 0.9992 0.9994 0.9994 0.9994 0.9992 0.9990 0.9988 0.9984 5 S 0.9981 0.9984 0.9987 0.9989 0.9990 0.9990 0.9990 0.9989 0.9987 0.9984 0.9981 Longitude (°) Latitude (°) 5 W 4 W 3 W 2 W 1 W 0 1 E 2 E 3 E 4 E 5 E 50 N 0.9985 0.9987 0.9988 0.9989 0.9989 0.9990 0.9989 0.9989 0.9988 0.9987 0.9985 49 N 0.9989 0.9990 0.9992 0.9992 0.9993 0.9993 0.9993 0.9992 0.9992 0.9990 0.9989 48 N 0.9991 0.9993 0.9994 0.9995 0.9996 0.9996 0.9996 0.9995
Load more

Recommended publications
  • Nicolas-Auguste Tissot: a Link Between Cartography and Quasiconformal Theory
    NICOLAS-AUGUSTE TISSOT: A LINK BETWEEN CARTOGRAPHY AND QUASICONFORMAL THEORY ATHANASE PAPADOPOULOS Abstract. Nicolas-Auguste Tissot (1824{1897) published a series of papers on cartography in which he introduced a tool which became known later on, among geographers, under the name of the Tissot indicatrix. This tool was broadly used during the twentieth century in the theory and in the practical aspects of the drawing of geographical maps. The Tissot indicatrix is a graph- ical representation of a field of ellipses on a map that describes its distortion. Tissot studied extensively, from a mathematical viewpoint, the distortion of mappings from the sphere onto the Euclidean plane that are used in drawing geographical maps, and more generally he developed a theory for the distor- sion of mappings between general surfaces. His ideas are at the heart of the work on quasiconformal mappings that was developed several decades after him by Gr¨otzsch, Lavrentieff, Ahlfors and Teichm¨uller.Gr¨otzsch mentions the work of Tissot and he uses the terminology related to his name (in particular, Gr¨otzsch uses the Tissot indicatrix). Teichm¨ullermentions the name of Tissot in a historical section in one of his fundamental papers where he claims that quasiconformal mappings were used by geographers, but without giving any hint about the nature of Tissot's work. The name of Tissot is also missing from all the historical surveys on quasiconformal mappings. In the present paper, we report on this work of Tissot. We shall also mention some related works on cartography, on the differential geometry of surfaces, and on the theory of quasiconformal mappings.
    [Show full text]
  • Understanding Map Projections
    Understanding Map Projections GIS by ESRI ™ Melita Kennedy and Steve Kopp Copyright © 19942000 Environmental Systems Research Institute, Inc. All rights reserved. Printed in the United States of America. The information contained in this document is the exclusive property of Environmental Systems Research Institute, Inc. This work is protected under United States copyright law and other international copyright treaties and conventions. No part of this work may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying and recording, or by any information storage or retrieval system, except as expressly permitted in writing by Environmental Systems Research Institute, Inc. All requests should be sent to Attention: Contracts Manager, Environmental Systems Research Institute, Inc., 380 New York Street, Redlands, CA 92373-8100, USA. The information contained in this document is subject to change without notice. U.S. GOVERNMENT RESTRICTED/LIMITED RIGHTS Any software, documentation, and/or data delivered hereunder is subject to the terms of the License Agreement. In no event shall the U.S. Government acquire greater than RESTRICTED/LIMITED RIGHTS. At a minimum, use, duplication, or disclosure by the U.S. Government is subject to restrictions as set forth in FAR §52.227-14 Alternates I, II, and III (JUN 1987); FAR §52.227-19 (JUN 1987) and/or FAR §12.211/12.212 (Commercial Technical Data/Computer Software); and DFARS §252.227-7015 (NOV 1995) (Technical Data) and/or DFARS §227.7202 (Computer Software), as applicable. Contractor/Manufacturer is Environmental Systems Research Institute, Inc., 380 New York Street, Redlands, CA 92373- 8100, USA.
    [Show full text]
  • Mercator-15Dec2015.Pdf
    THE MERCATOR PROJECTIONS THE NORMAL AND TRANSVERSE MERCATOR PROJECTIONS ON THE SPHERE AND THE ELLIPSOID WITH FULL DERIVATIONS OF ALL FORMULAE PETER OSBORNE EDINBURGH 2013 This article describes the mathematics of the normal and transverse Mercator projections on the sphere and the ellipsoid with full deriva- tions of all formulae. The Transverse Mercator projection is the basis of many maps cov- ering individual countries, such as Australia and Great Britain, as well as the set of UTM projections covering the whole world (other than the polar regions). Such maps are invariably covered by a set of grid lines. It is important to appreciate the following two facts about the Transverse Mercator projection and the grids covering it: 1. Only one grid line runs true north–south. Thus in Britain only the grid line coincident with the central meridian at 2◦W is true: all other meridians deviate from grid lines. The UTM series is a set of 60 distinct Transverse Mercator projections each covering a width of 6◦in latitude: the grid lines run true north–south only on the central meridians at 3◦E, 9◦E, 15◦E, ... 2. The scale on the maps derived from Transverse Mercator pro- jections is not uniform: it is a function of position. For ex- ample the Landranger maps of the Ordnance Survey of Great Britain have a nominal scale of 1:50000: this value is only ex- act on two slightly curved lines almost parallel to the central meridian at 2◦W and distant approximately 180km east and west of it. The scale on the central meridian is constant but it is slightly less than the nominal value.
    [Show full text]
  • An Efficient Technique for Creating a Continuum of Equal-Area Map Projections
    Cartography and Geographic Information Science ISSN: 1523-0406 (Print) 1545-0465 (Online) Journal homepage: http://www.tandfonline.com/loi/tcag20 An efficient technique for creating a continuum of equal-area map projections Daniel “daan” Strebe To cite this article: Daniel “daan” Strebe (2017): An efficient technique for creating a continuum of equal-area map projections, Cartography and Geographic Information Science, DOI: 10.1080/15230406.2017.1405285 To link to this article: https://doi.org/10.1080/15230406.2017.1405285 View supplementary material Published online: 05 Dec 2017. Submit your article to this journal View related articles View Crossmark data Full Terms & Conditions of access and use can be found at http://www.tandfonline.com/action/journalInformation?journalCode=tcag20 Download by: [4.14.242.133] Date: 05 December 2017, At: 13:13 CARTOGRAPHY AND GEOGRAPHIC INFORMATION SCIENCE, 2017 https://doi.org/10.1080/15230406.2017.1405285 ARTICLE An efficient technique for creating a continuum of equal-area map projections Daniel “daan” Strebe Mapthematics LLC, Seattle, WA, USA ABSTRACT ARTICLE HISTORY Equivalence (the equal-area property of a map projection) is important to some categories of Received 4 July 2017 maps. However, unlike for conformal projections, completely general techniques have not been Accepted 11 November developed for creating new, computationally reasonable equal-area projections. The literature 2017 describes many specific equal-area projections and a few equal-area projections that are more or KEYWORDS less configurable, but flexibility is still sparse. This work develops a tractable technique for Map projection; dynamic generating a continuum of equal-area projections between two chosen equal-area projections.
    [Show full text]
  • Comparison of Spherical Cube Map Projections Used in Planet-Sized Terrain Rendering
    FACTA UNIVERSITATIS (NIS)ˇ Ser. Math. Inform. Vol. 31, No 2 (2016), 259–297 COMPARISON OF SPHERICAL CUBE MAP PROJECTIONS USED IN PLANET-SIZED TERRAIN RENDERING Aleksandar M. Dimitrijevi´c, Martin Lambers and Dejan D. Ranˇci´c Abstract. A wide variety of projections from a planet surface to a two-dimensional map are known, and the correct choice of a particular projection for a given application area depends on many factors. In the computer graphics domain, in particular in the field of planet rendering systems, the importance of that choice has been neglected so far and inadequate criteria have been used to select a projection. In this paper, we derive evaluation criteria, based on texture distortion, suitable for this application domain, and apply them to a comprehensive list of spherical cube map projections to demonstrate their properties. Keywords: Map projection, spherical cube, distortion, texturing, graphics 1. Introduction Map projections have been used for centuries to represent the curved surface of the Earth with a two-dimensional map. A wide variety of map projections have been proposed, each with different properties. Of particular interest are scale variations and angular distortions introduced by map projections – since the spheroidal surface is not developable, a projection onto a plane cannot be both conformal (angle- preserving) and equal-area (constant-scale) at the same time. These two properties are usually analyzed using Tissot’s indicatrix. An overview of map projections and an introduction to Tissot’s indicatrix are given by Snyder [24]. In computer graphics, a map projection is a central part of systems that render planets or similar celestial bodies: the surface properties (photos, digital elevation models, radar imagery, thermal measurements, etc.) are stored in a map hierarchy in different resolutions.
    [Show full text]
  • The Light Source Metaphor Revisited—Bringing an Old Concept for Teaching Map Projections to the Modern Web
    International Journal of Geo-Information Article The Light Source Metaphor Revisited—Bringing an Old Concept for Teaching Map Projections to the Modern Web Magnus Heitzler 1,* , Hans-Rudolf Bär 1, Roland Schenkel 2 and Lorenz Hurni 1 1 Institute of Cartography and Geoinformation, ETH Zurich, 8049 Zurich, Switzerland; [email protected] (H.-R.B.); [email protected] (L.H.) 2 ESRI Switzerland, 8005 Zurich, Switzerland; [email protected] * Correspondence: [email protected] Received: 28 February 2019; Accepted: 24 March 2019; Published: 28 March 2019 Abstract: Map projections are one of the foundations of geographic information science and cartography. An understanding of the different projection variants and properties is critical when creating maps or carrying out geospatial analyses. The common way of teaching map projections in text books makes use of the light source (or light bulb) metaphor, which draws a comparison between the construction of a map projection and the way light rays travel from the light source to the projection surface. Although conceptually plausible, such explanations were created for the static instructions in textbooks. Modern web technologies may provide a more comprehensive learning experience by allowing the student to interactively explore (in guided or unguided mode) the way map projections can be constructed following the light source metaphor. The implementation of this approach, however, is not trivial as it requires detailed knowledge of map projections and computer graphics. Therefore, this paper describes the underlying computational methods and presents a prototype as an example of how this concept can be applied in practice. The prototype will be integrated into the Geographic Information Technology Training Alliance (GITTA) platform to complement the lesson on map projections.
    [Show full text]
  • Map Projections
    Map Projections Chapter 4 Map Projections What is map projection? Why are map projections drawn? What are the different types of projections? Which projection is most suitably used for which area? In this chapter, we will seek the answers of such essential questions. MAP PROJECTION Map projection is the method of transferring the graticule of latitude and longitude on a plane surface. It can also be defined as the transformation of spherical network of parallels and meridians on a plane surface. As you know that, the earth on which we live in is not flat. It is geoid in shape like a sphere. A globe is the best model of the earth. Due to this property of the globe, the shape and sizes of the continents and oceans are accurately shown on it. It also shows the directions and distances very accurately. The globe is divided into various segments by the lines of latitude and longitude. The horizontal lines represent the parallels of latitude and the vertical lines represent the meridians of the longitude. The network of parallels and meridians is called graticule. This network facilitates drawing of maps. Drawing of the graticule on a flat surface is called projection. But a globe has many limitations. It is expensive. It can neither be carried everywhere easily nor can a minor detail be shown on it. Besides, on the globe the meridians are semi-circles and the parallels 35 are circles. When they are transferred on a plane surface, they become intersecting straight lines or curved lines. 2021-22 Practical Work in Geography NEED FOR MAP PROJECTION The need for a map projection mainly arises to have a detailed study of a 36 region, which is not possible to do from a globe.
    [Show full text]
  • How to Determine Latitude and Longitude from Topographic Maps
    Oregon Department of Environmental Quality HOW TO DETERMINE LATITUDE AND LONGITUDE FROM TOPOGRAPHIC MAPS Latitude is the distance north or south of the equator. 2. For each location, construct a small rectangle around Longitude is the distance east or west of the prime the point with fine pencil lines connecting the nearest meridian (Greenwich, England). Latitude and longitude 2-1/2′ or 5′ graticules. Graticules are intersections of are measured in seconds, minutes, and degrees: latitude and longitude lines that are marked on the map edge, and appear as black crosses at four points in ″ ′ 60 (seconds) = 1 (minute) the interior of the map. 60′ (minutes) = 1° (degree) 3. Read and record the latitude and longitude for the To determine the latitude and longitude of your facility, southeast corner of the small quadrangle drawn in step you will need a topographic map from United States two. The latitude and longitude are printed at the edges Geological Survey (USGS). of the map. How to Obtain USGS Maps: 4. To determine the increment of latitude above the latitude line recorded in step 3: USGS maps used for determining latitude and longitude • Position the map so that you face its west edge; may be obtained from the USGS distribution center. These maps are available in both the 7.5 minute and l5 • Place the ruler in approximately a north-south minute series. For maps of the United States, including alignment, with the “0” on the latitude line recorded Alaska, Hawaii, American Samoa, Guam, Puerto Rico, in step 3 and the edge intersecting the point.
    [Show full text]
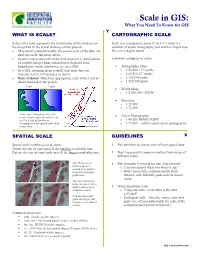
  • Scale in GIS: What You Need to Know for GIS
    Scale in GIS: What You Need To Know for GIS Y WHAT IS SCALE? CARTOGRAPHIC SCALE Scale is the scale represents the relationship of the distance on Scale in a cartographic sense (1 inch = 1 mile) is a the map/data to the actual distance on the ground. remnant of vector cartography, but still has importance • Map detail is determined by the source scale of the data: the for us in a digital world. finer the scale, the more detail. • Source scale is the scale of the data source (i.e. aerial photo Common cartographic scales: or satellite image) from which data is digitized (into boundaries, roads, landcover, etc. in a GIS). • Topographic Maps • In a GIS, zooming in on a small scale map does not o 1:24,000 7.5” quads increase its level of accuracy or detail. o 1:63,360 15” quads • Rule of thumb: Match the appropriate scale to the level of o 1:100,000 quads detail required in the project. o 1:250,000 quads 1:500 1:1200 • World Maps o 1:2,000,000 – DCW • Shoreline o 1:20,000 o 1:70,000 Above, right. Comparing fine and coarse source scales shows how the • Aerial Photography level of detail in the data is o 1:40,000 NHAP/NAPP determined by the spatial scale of the o 1:12,000 – 4,000 custom aerial photography source data. SPATIAL SCALE GUIDELINES X Spatial scale involves grain & extent: 1. Pay attention to source scale of your spatial data. Grain: the size of your pixel & the smallest resolvable unit.
    [Show full text]
  • Healpix Mapping Technique and Cartographical Application Omur Esen , Vahit Tongur , Ismail Bulent Gundogdu Abstract Hierarchical
    HEALPix Mapping Technique and Cartographical Application Omur Esen1, Vahit Tongur2, Ismail Bulent Gundogdu3 1Selcuk University, Construction Offices and Infrastructure Presidency, [email protected] 2Necmettin Erbakan University, Computer Engineering Department of Engineering and Architecture Faculty, [email protected] 3Selcuk University, Geomatics Engineering Department of Engineering Faculty, [email protected] Abstract Hierarchical Equal Area isoLatitude Pixelization (HEALPix) system is defined as a layer which is used in modern astronomy for using pixelised data, which are required by developed detectors, for a fast true and proper scientific comment of calculation algoritms on spherical maps. HEALPix system is developed by experiments which are generally used in astronomy and called as Cosmic Microwave Background (CMB). HEALPix system reminds fragment of a sphere into 12 equal equilateral diamonds. In this study aims to make a litetature study for mapping of the world by mathematical equations of HEALPix celling/tesellation system in cartographical map making method and calculating and examining deformation values by Gauss Fundamental Equations. So, although HEALPix system is known as equal area until now, it is shown that this celling system do not provide equal area cartographically. Keywords: Cartography, Equal Area, HEALPix, Mapping 1. INTRODUCTION Map projection, which is classically defined as portraying of world on a plane, is effected by technological developments. Considering latest technological developments, we can offer definition of map projection as “3d and time varying space, it is the transforming techniques of space’s, earth’s and all or part of other objects photos in a described coordinate system by keeping positions proper and specific features on a plane by using mathematical relation.” Considering today’s technological developments, cartographical projections are developing on multi surfaces (polihedron) and Myriahedral projections which is used by Wijk (2008) for the first time.
    [Show full text]
  • Maps and Cartography: Map Projections a Tutorial Created by the GIS Research & Map Collection
    Maps and Cartography: Map Projections A Tutorial Created by the GIS Research & Map Collection Ball State University Libraries A destination for research, learning, and friends What is a map projection? Map makers attempt to transfer the earth—a round, spherical globe—to flat paper. Map projections are the different techniques used by cartographers for presenting a round globe on a flat surface. Angles, areas, directions, shapes, and distances can become distorted when transformed from a curved surface to a plane. Different projections have been designed where the distortion in one property is minimized, while other properties become more distorted. So map projections are chosen based on the purposes of the map. Keywords •azimuthal: projections with the property that all directions (azimuths) from a central point are accurate •conformal: projections where angles and small areas’ shapes are preserved accurately •equal area: projections where area is accurate •equidistant: projections where distance from a standard point or line is preserved; true to scale in all directions •oblique: slanting, not perpendicular or straight •rhumb lines: lines shown on a map as crossing all meridians at the same angle; paths of constant bearing •tangent: touching at a single point in relation to a curve or surface •transverse: at right angles to the earth’s axis Models of Map Projections There are two models for creating different map projections: projections by presentation of a metric property and projections created from different surfaces. • Projections by presentation of a metric property would include equidistant, conformal, gnomonic, equal area, and compromise projections. These projections account for area, shape, direction, bearing, distance, and scale.
    [Show full text]
  • Map Projections and Coordinate Systems Datums Tell Us the Latitudes and Longi- Vertex, Node, Or Grid Cell in a Data Set, Con- Tudes of Features on an Ellipsoid
    116 GIS Fundamentals Map Projections and Coordinate Systems Datums tell us the latitudes and longi- vertex, node, or grid cell in a data set, con- tudes of features on an ellipsoid. We need to verting the vector or raster data feature by transfer these from the curved ellipsoid to a feature from geographic to Mercator coordi- flat map. A map projection is a systematic nates. rendering of locations from the curved Earth Notice that there are parameters we surface onto a flat map surface. must specify for this projection, here R, the Nearly all projections are applied via Earth’s radius, and o, the longitudinal ori- exact or iterated mathematical formulas that gin. Different values for these parameters convert between geographic latitude and give different values for the coordinates, so longitude and projected X an Y (Easting and even though we may have the same kind of Northing) coordinates. Figure 3-30 shows projection (transverse Mercator), we have one of the simpler projection equations, different versions each time we specify dif- between Mercator and geographic coordi- ferent parameters. nates, assuming a spherical Earth. These Projection equations must also be speci- equations would be applied for every point, fied in the “backward” direction, from pro- jected coordinates to geographic coordinates, if they are to be useful. The pro- jection coordinates in this backward, or “inverse,” direction are often much more complicated that the forward direction, but are specified for every commonly used pro- jection. Most projection equations are much more complicated than the transverse Mer- cator, in part because most adopt an ellipsoi- dal Earth, and because the projections are onto curved surfaces rather than a plane, but thankfully, projection equations have long been standardized, documented, and made widely available through proven programing libraries and projection calculators.
    [Show full text]