Comparison of Spherical Cube Map Projections Used in Planet-Sized Terrain Rendering
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Seamscape a Procedural Generation System for Accelerated Creation of 3D Landscapes
SeamScape A procedural generation system for accelerated creation of 3D landscapes Bachelor Thesis in Computer Science and Engineering Link to video demonstration: youtu.be/K5yaTmksIOM Sebastian Ekman Anders Hansson Thomas Högberg Anna Nylander Alma Ottedag Joakim Thorén Chalmers University of Technology University of Gothenburg Department of Computer Science and Engineering Gothenburg, Sweden, June 2016 The Authors grants to Chalmers University of Technology and University of Gothenburg the non-exclusive right to publish the Work electronically and in a non-commercial purpose make it accessible on the Internet. The Author warrants that he/she is the author to the Work, and warrants that the Work does not contain text, pictures or other material that violates copyright law. The Author shall, when transferring the rights of the Work to a third party (for example a publisher or a company), acknowledge the third party about this agreement. If the Author has signed a copyright agreement with a third party regarding the Work, the Author warrants hereby that he/she has obtained any necessary permission from this third party to let Chalmers University of Technology and University of Gothenburg store the Work electronically and make it accessible on the Internet. SeamScape A procedural generation system for accelerated creation of 3D landscapes Sebastian Ekman Anders Hansson Thomas Högberg Anna Nylander Alma Ottedag Joakim Thorén c Sebastian Ekman, 2016. c Anders Hansson, 2016. c Thomas Högberg, 2016. c Anna Nylander, 2016. c Alma Ottedag, 2016. -

Analyze a World Map
Analyze a World Map Materials: Map of the World: Political or use link this website Map of the World Worksheet You could start the discussion by saying that the social studies part of the GED test assumes that everyone has a basic knowledge of world geography. The test will contain maps that you have to analyze and the answers are not always directly on the map. This is one area of the test where they expect you to just know the approximate locations of countries and oceans. So we thought we would use this world map to familiarize everyone with some world geography. Hand out the maps. The first thing you need to do with a map is read the title so that you know what you are looking at. Ask, “What is the title of this map?” ‘Map of the World: Political”. So this map should give us information about the location of countries. Then look to see if there is a legend or a list of symbols that explains the information shown on the map. Ask, “Is there a legend for this map/” Yes, it shows the scale of the map. You can discuss that the scale shows the relationship between distances on the map to the actual distance on the ground. Look to see if there is anything on the map showing directions, most maps have a compass that shows east, west, north, and south. Ask, “Does this map have any symbols indicating direction?” Yes, this map has a direction compass that shows points north. Ask if students know where south, east, and west are on the map. -

Understanding Map Projections
Understanding Map Projections GIS by ESRI ™ Melita Kennedy and Steve Kopp Copyright © 19942000 Environmental Systems Research Institute, Inc. All rights reserved. Printed in the United States of America. The information contained in this document is the exclusive property of Environmental Systems Research Institute, Inc. This work is protected under United States copyright law and other international copyright treaties and conventions. No part of this work may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying and recording, or by any information storage or retrieval system, except as expressly permitted in writing by Environmental Systems Research Institute, Inc. All requests should be sent to Attention: Contracts Manager, Environmental Systems Research Institute, Inc., 380 New York Street, Redlands, CA 92373-8100, USA. The information contained in this document is subject to change without notice. U.S. GOVERNMENT RESTRICTED/LIMITED RIGHTS Any software, documentation, and/or data delivered hereunder is subject to the terms of the License Agreement. In no event shall the U.S. Government acquire greater than RESTRICTED/LIMITED RIGHTS. At a minimum, use, duplication, or disclosure by the U.S. Government is subject to restrictions as set forth in FAR §52.227-14 Alternates I, II, and III (JUN 1987); FAR §52.227-19 (JUN 1987) and/or FAR §12.211/12.212 (Commercial Technical Data/Computer Software); and DFARS §252.227-7015 (NOV 1995) (Technical Data) and/or DFARS §227.7202 (Computer Software), as applicable. Contractor/Manufacturer is Environmental Systems Research Institute, Inc., 380 New York Street, Redlands, CA 92373- 8100, USA. -

An Efficient Technique for Creating a Continuum of Equal-Area Map Projections
Cartography and Geographic Information Science ISSN: 1523-0406 (Print) 1545-0465 (Online) Journal homepage: http://www.tandfonline.com/loi/tcag20 An efficient technique for creating a continuum of equal-area map projections Daniel “daan” Strebe To cite this article: Daniel “daan” Strebe (2017): An efficient technique for creating a continuum of equal-area map projections, Cartography and Geographic Information Science, DOI: 10.1080/15230406.2017.1405285 To link to this article: https://doi.org/10.1080/15230406.2017.1405285 View supplementary material Published online: 05 Dec 2017. Submit your article to this journal View related articles View Crossmark data Full Terms & Conditions of access and use can be found at http://www.tandfonline.com/action/journalInformation?journalCode=tcag20 Download by: [4.14.242.133] Date: 05 December 2017, At: 13:13 CARTOGRAPHY AND GEOGRAPHIC INFORMATION SCIENCE, 2017 https://doi.org/10.1080/15230406.2017.1405285 ARTICLE An efficient technique for creating a continuum of equal-area map projections Daniel “daan” Strebe Mapthematics LLC, Seattle, WA, USA ABSTRACT ARTICLE HISTORY Equivalence (the equal-area property of a map projection) is important to some categories of Received 4 July 2017 maps. However, unlike for conformal projections, completely general techniques have not been Accepted 11 November developed for creating new, computationally reasonable equal-area projections. The literature 2017 describes many specific equal-area projections and a few equal-area projections that are more or KEYWORDS less configurable, but flexibility is still sparse. This work develops a tractable technique for Map projection; dynamic generating a continuum of equal-area projections between two chosen equal-area projections. -

Countries and Continents of the World: a Visual Model
Countries and Continents of the World http://geology.com/world/world-map-clickable.gif By STF Members at The Crossroads School Africa Second largest continent on earth (30,065,000 Sq. Km) Most countries of any other continent Home to The Sahara, the largest desert in the world and The Nile, the longest river in the world The Sahara: covers 4,619,260 km2 The Nile: 6695 kilometers long There are over 1000 languages spoken in Africa http://www.ecdc-cari.org/countries/Africa_Map.gif North America Third largest continent on earth (24,256,000 Sq. Km) Composed of 23 countries Most North Americans speak French, Spanish, and English Only continent that has every kind of climate http://www.freeusandworldmaps.com/html/WorldRegions/WorldRegions.html Asia Largest continent in size and population (44,579,000 Sq. Km) Contains 47 countries Contains the world’s largest country, Russia, and the most populous country, China The Great Wall of China is the only man made structure that can be seen from space Home to Mt. Everest (on the border of Tibet and Nepal), the highest point on earth Mt. Everest is 29,028 ft. (8,848 m) tall http://craigwsmall.wordpress.com/2008/11/10/asia/ Europe Second smallest continent in the world (9,938,000 Sq. Km) Home to the smallest country (Vatican City State) There are no deserts in Europe Contains mineral resources: coal, petroleum, natural gas, copper, lead, and tin http://www.knowledgerush.com/wiki_image/b/bf/Europe-large.png Oceania/Australia Smallest continent on earth (7,687,000 Sq. -
![Rcosmo: R Package for Analysis of Spherical, Healpix and Cosmological Data Arxiv:1907.05648V1 [Stat.CO] 12 Jul 2019](https://docslib.b-cdn.net/cover/0993/rcosmo-r-package-for-analysis-of-spherical-healpix-and-cosmological-data-arxiv-1907-05648v1-stat-co-12-jul-2019-240993.webp)
Rcosmo: R Package for Analysis of Spherical, Healpix and Cosmological Data Arxiv:1907.05648V1 [Stat.CO] 12 Jul 2019
CONTRIBUTED RESEARCH ARTICLE 1 rcosmo: R Package for Analysis of Spherical, HEALPix and Cosmological Data Daniel Fryer, Ming Li, Andriy Olenko Abstract The analysis of spatial observations on a sphere is important in areas such as geosciences, physics and embryo research, just to name a few. The purpose of the package rcosmo is to conduct efficient information processing, visualisation, manipulation and spatial statistical analysis of Cosmic Microwave Background (CMB) radiation and other spherical data. The package was developed for spherical data stored in the Hierarchical Equal Area isoLatitude Pixelation (Healpix) representation. rcosmo has more than 100 different functions. Most of them initially were developed for CMB, but also can be used for other spherical data as rcosmo contains tools for transforming spherical data in cartesian and geographic coordinates into the HEALPix representation. We give a general description of the package and illustrate some important functionalities and benchmarks. Introduction Directional statistics deals with data observed at a set of spatial directions, which are usually positioned on the surface of the unit sphere or star-shaped random particles. Spherical methods are important research tools in geospatial, biological, palaeomagnetic and astrostatistical analysis, just to name a few. The books (Fisher et al., 1987; Mardia and Jupp, 2009) provide comprehensive overviews of classical practical spherical statistical methods. Various stochastic and statistical inference modelling issues are covered in (Yadrenko, 1983; Marinucci and Peccati, 2011). The CRAN Task View Spatial shows several packages for Earth-referenced data mapping and analysis. All currently available R packages for spherical data can be classified in three broad groups. The first group provides various functions for working with geographic and spherical coordinate systems and their visualizations. -

The Uses of Animation 1
The Uses of Animation 1 1 The Uses of Animation ANIMATION Animation is the process of making the illusion of motion and change by means of the rapid display of a sequence of static images that minimally differ from each other. The illusion—as in motion pictures in general—is thought to rely on the phi phenomenon. Animators are artists who specialize in the creation of animation. Animation can be recorded with either analogue media, a flip book, motion picture film, video tape,digital media, including formats with animated GIF, Flash animation and digital video. To display animation, a digital camera, computer, or projector are used along with new technologies that are produced. Animation creation methods include the traditional animation creation method and those involving stop motion animation of two and three-dimensional objects, paper cutouts, puppets and clay figures. Images are displayed in a rapid succession, usually 24, 25, 30, or 60 frames per second. THE MOST COMMON USES OF ANIMATION Cartoons The most common use of animation, and perhaps the origin of it, is cartoons. Cartoons appear all the time on television and the cinema and can be used for entertainment, advertising, 2 Aspects of Animation: Steps to Learn Animated Cartoons presentations and many more applications that are only limited by the imagination of the designer. The most important factor about making cartoons on a computer is reusability and flexibility. The system that will actually do the animation needs to be such that all the actions that are going to be performed can be repeated easily, without much fuss from the side of the animator. -

Geography Notes.Pdf
THE GLOBE What is a globe? a small model of the Earth Parts of a globe: equator - the line on the globe halfway between the North Pole and the South Pole poles - the northern-most and southern-most points on the Earth 1. North Pole 2. South Pole hemispheres - half of the earth, divided by the equator (North & South) and the prime meridian (East and West) 1. Northern Hemisphere 2. Southern Hemisphere 3. Eastern Hemisphere 4. Western Hemisphere continents - the largest land areas on Earth 1. North America 2. South America 3. Europe 4. Asia 5. Africa 6. Australia 7. Antarctica oceans - the largest water areas on Earth 1. Atlantic Ocean 2. Pacific Ocean 3. Indian Ocean 4. Arctic Ocean 5. Antarctic Ocean WORLD MAP ** NOTE: Our textbooks call the “Southern Ocean” the “Antarctic Ocean” ** North America The three major countries of North America are: 1. Canada 2. United States 3. Mexico Where Do We Live? We live in the Western & Northern Hemispheres. We live on the continent of North America. The other 2 large countries on this continent are Canada and Mexico. The name of our country is the United States. There are 50 states in it, but when it first became a country, there were only 13 states. The name of our state is New York. Its capital city is Albany. GEOGRAPHY STUDY GUIDE You will need to know: VOCABULARY: equator globe hemisphere continent ocean compass WORLD MAP - be able to label 7 continents and 5 oceans 3 Large Countries of North America 1. United States 2. Canada 3. -

Was This World Map Made Ten Centuries Ago?
HAWAIIAN GAZETTE, FRIDAY, JANUARY n, 1907 SEMI-WEEKL- Y Was This World Map Made Ten Centuries Ago? gg "J" ISOME DETAILS OF GREAT Vf? rr9rv-vr- i 'vir)('JK.rr KXW XXXjtXXmXmKiXXXiXXX XvyXXXrXXX ffKftXr1 STORM Politically Inclined policemen nro not wanted by tho new Sheriff, who will MAUI, shortly Issue nn order to the effect that January i. The holiday sea- son 2 i I nlj employes of tho police department on Maul has not been a tlmo of quiet 5 j ft must chooso between their Jobs on tho enjoyment ns far as weather is 5 a force and their oITlces In any of tho concerned. Dame Nnturo has echoed A.- -. a. w three political party committees. This anything but the Christmas sentiment rule Is to bo strictly enforced, the em of "peace on earth and good-wi- lt ployes of tho public being supposed, bo mn." far as tho police are concernod at least, Before recovery could bo made from to give their time and energy to th tho effects of the recent north storm public and not for the advancement with Its 20 Inches of moisture In local- politically or otherwlso of any one sec- ities, on Saturday tho wind changed Ifr tion of tho public to the southucst and nn kona Tho Sheriff Is making plain storm came Into being. It contin- If It that ued to blow fiercely ho means ho says all tho night what when he tabued through, accompanied by nn Incessant i - i politics around tho police station. In piny of lightning and the heavy roll of this he has come In for moro or less thunder. -

Game Engine Review
Game Engine Review Mr. Stuart Armstrong 12565 Research Parkway, Suite 350 Orlando FL, 32826 USA [email protected] ABSTRACT There has been a significant amount of interest around the use of Commercial Off The Shelf products to support military training and education. This paper compares a number of current game engines available on the market and assesses them against potential military simulation criteria. 1.0 GAMES IN DEFENSE “A game is a system in which players engage in an artificial conflict, defined by rules, which result in a quantifiable outcome.” The use of games for defence simulation can be broadly split into two categories – the use of game technologies to provide an immersive and flexible military training system and a “serious game” that uses game design principles (such as narrative and scoring) to deliver education and training content in a novel way. This talk and subsequent education notes focus on the use of game technologies, in particular game engines to support military training. 2.0 INTRODUCTION TO GAMES ENGINES “A games engine is a software suite designed to facilitate the production of computer games.” Developers use games engines to create games for games consoles, personal computers and growingly mobile devices. Games engines provide a flexible and reusable development toolkit with all the core functionality required to produce a game quickly and efficiently. Multiple games can be produced from the same games engine, for example Counter Strike Source, Half Life 2 and Left 4 Dead 2 are all created using the Source engine. Equally once created, the game source code can with little, if any modification be abstracted for different gaming platforms such as a Playstation, Personal Computer or Wii. -

Notes on Projections Part II - Common Projections James R
Notes on Projections Part II - Common Projections James R. Clynch 2003 I. Common Projections There are several areas where maps are commonly used and a few projections dominate these fields. An extensive list is given at the end of the Introduction Chapter in Snyder. Here just a few will be given. Whole World Mercator Most common world projection. Cylindrical Robinson Less distortion than Mercator. Pseudocylindrical Goode Interrupted map. Common for thematic maps. Navigation Charts UTM Common for ocean charts. Part of military map system. UPS For polar regions. Part of military map system. Lambert Lambert Conformal Conic standard in Air Navigation Charts Topographic Maps Polyconic US Geological Survey Standard. UTM coordinates on margins. Surveying / Land Use / General Adlers Equal Area (Conic) Transverse Mercator For areas mainly North-South Lambert For areas mainly East-West A discussion of these and a few others follows. For an extensive list see Snyder. The two maps that form the military grid reference system (MGRS) the UTM and UPS are discussed in detail in a separate note. II. Azimuthal or Planar Projections I you project a globe on a plane that is tangent or symmetric about the polar axis the azimuths to the center point are all true. This leads to the name Azimuthal for projections on a plane. There are 4 common projections that use a plane as the projection surface. Three are perspective. The fourth is the simple polar plot that has the official name equidistant azimuthal projection. The three perspective azimuthal projections are shown below. They differ in the location of the perspective or projection point. -
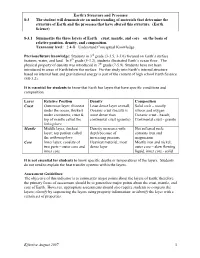
Earth's Structure and Processes 8-3 the Student Will Demonstrate An
Earth’s Structure and Processes 8-3 The student will demonstrate an understanding of materials that determine the structure of Earth and the processes that have altered this structure. (Earth Science) 8-3.1 Summarize the three layers of Earth – crust, mantle, and core – on the basis of relative position, density, and composition. Taxonomy level: 2.4-B Understand Conceptual Knowledge Previous/future knowledge: Students in 3rd grade (3-3.5, 3-3.6) focused on Earth’s surface features, water, and land. In 5th grade (5-3.2), students illustrated Earth’s ocean floor. The physical property of density was introduced in 7th grade (7-5.9). Students have not been introduced to areas of Earth below the surface. Further study into Earth’s internal structure based on internal heat and gravitational energy is part of the content of high school Earth Science (ES-3.2). It is essential for students to know that Earth has layers that have specific conditions and composition. Layer Relative Position Density Composition Crust Outermost layer; thinnest Least dense layer overall; Solid rock – mostly under the ocean, thickest Oceanic crust (basalt) is silicon and oxygen under continents; crust & more dense than Oceanic crust - basalt; top of mantle called the continental crust (granite) Continental crust - granite lithosphere Mantle Middle layer, thickest Density increases with Hot softened rock; layer; top portion called depth because of contains iron and the asthenosphere increasing pressure magnesium Core Inner layer; consists of Heaviest material; most Mostly iron and nickel; two parts – outer core and dense layer outer core – slow flowing inner core liquid, inner core - solid It is not essential for students to know specific depths or temperatures of the layers.