Metric Guide for Federal Construction (4-93)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Nicolas-Auguste Tissot: a Link Between Cartography and Quasiconformal Theory
NICOLAS-AUGUSTE TISSOT: A LINK BETWEEN CARTOGRAPHY AND QUASICONFORMAL THEORY ATHANASE PAPADOPOULOS Abstract. Nicolas-Auguste Tissot (1824{1897) published a series of papers on cartography in which he introduced a tool which became known later on, among geographers, under the name of the Tissot indicatrix. This tool was broadly used during the twentieth century in the theory and in the practical aspects of the drawing of geographical maps. The Tissot indicatrix is a graph- ical representation of a field of ellipses on a map that describes its distortion. Tissot studied extensively, from a mathematical viewpoint, the distortion of mappings from the sphere onto the Euclidean plane that are used in drawing geographical maps, and more generally he developed a theory for the distor- sion of mappings between general surfaces. His ideas are at the heart of the work on quasiconformal mappings that was developed several decades after him by Gr¨otzsch, Lavrentieff, Ahlfors and Teichm¨uller.Gr¨otzsch mentions the work of Tissot and he uses the terminology related to his name (in particular, Gr¨otzsch uses the Tissot indicatrix). Teichm¨ullermentions the name of Tissot in a historical section in one of his fundamental papers where he claims that quasiconformal mappings were used by geographers, but without giving any hint about the nature of Tissot's work. The name of Tissot is also missing from all the historical surveys on quasiconformal mappings. In the present paper, we report on this work of Tissot. We shall also mention some related works on cartography, on the differential geometry of surfaces, and on the theory of quasiconformal mappings. -

Estimating Highway Maintenance Work Indiana LTAP Center
Estimating Highway Maintenance Work July 2011 SP-1-2011 compiled by The Ohio Department of Transportation updated by The Indiana LTAP Center Indiana LTAP Center Purdue University School of Civil Engineering Indiana LTAP Center 3000 Kent Avenue West Lafayette, Indiana 47906 Telephone: 765.494.2164 Toll Free in Indiana: 1.800.428.7639 Facsimile: 765.496.1176 This document is disseminated under the sponsorship of the Indiana LTAP Center at Purdue University in the interest of information exchange. Purdue University and the Indiana LTAP Center assume no liability for its contents or use thereof. Purdue University and the Indiana LTAP Center do not endorse products or manufacturers. Trademarks or manufacturers names may appear herein only because they are considered essential to the objective of this document. The contents of this report reflect the views of the authors, who are responsible for the facts and accuracy of the data presented herein. The contents do not necessarily reflect the official policy of Purdue University or the Indiana LTAP Center. This report does not constitute a standard, specification, or regulation. Estimating Highway Maintenance Work Estimating amounts of materials, work done, size of crews, or number of trucks needed for road maintenance requires the skill of working with NUMBERS and MEASUREMENTS . By using addition, subtraction, multiplication, division and some basic rules, you can do some figuring ahead of time and make your crews look better. People feel better about themselves when they’re doing a good job, their friends do too, and so does the motoring public. NUMBERS play an important part in the everyday affairs of everybody. -

Mercator-15Dec2015.Pdf
THE MERCATOR PROJECTIONS THE NORMAL AND TRANSVERSE MERCATOR PROJECTIONS ON THE SPHERE AND THE ELLIPSOID WITH FULL DERIVATIONS OF ALL FORMULAE PETER OSBORNE EDINBURGH 2013 This article describes the mathematics of the normal and transverse Mercator projections on the sphere and the ellipsoid with full deriva- tions of all formulae. The Transverse Mercator projection is the basis of many maps cov- ering individual countries, such as Australia and Great Britain, as well as the set of UTM projections covering the whole world (other than the polar regions). Such maps are invariably covered by a set of grid lines. It is important to appreciate the following two facts about the Transverse Mercator projection and the grids covering it: 1. Only one grid line runs true north–south. Thus in Britain only the grid line coincident with the central meridian at 2◦W is true: all other meridians deviate from grid lines. The UTM series is a set of 60 distinct Transverse Mercator projections each covering a width of 6◦in latitude: the grid lines run true north–south only on the central meridians at 3◦E, 9◦E, 15◦E, ... 2. The scale on the maps derived from Transverse Mercator pro- jections is not uniform: it is a function of position. For ex- ample the Landranger maps of the Ordnance Survey of Great Britain have a nominal scale of 1:50000: this value is only ex- act on two slightly curved lines almost parallel to the central meridian at 2◦W and distant approximately 180km east and west of it. The scale on the central meridian is constant but it is slightly less than the nominal value. -

Panama City, Florida Planning 101
Get a handle on how to effectively & rapidly manuever the development order processes of the City PANAMA CITY, FLORIDA PLANNING 101 PLA NNING DEPA City of Panama City, FLRTMENT UN IFIED LAND D EVELOPMEN A Referen T CODE ce Guide for the Citizens! 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 defi nitions enforcement nonconformities concurrency sign subdivision supplemental public parking landscaping environment design zoning review admin. general management standards of land standards improvements & loading & buff ering protection standards districts authority processes City of Panama City, FL City, Panama of City Unifi Code ed Land Development Unified Land Development Code Chapter 101 - GENERAL Page 1- 1 section The provisions of this Unified Land Development general CHAPTER 101 – GENERAL Code are declared to be the minimum require- 1 ments necessary to protect human, environmen- tal, social, and economic resources; and to main- processes Sec. 101-1. Title. This Chapter shall be entitled and tain, through orderly growth, and development, admin. may be referred to as the Unified Land Development and redevelopment the character and stability of 2 Code (“ULDC”). present and future land use within the city. authority Sec. 101-2. Purpose and Intent. This ULDC is enact- review Sec. 101-3. - Interpretation. The following rules 3 ed pursuant to the requirements and authority of F.S. of interpretation and construction shall apply to Ch. 163, pt. II (the Local Government Comprehensive this ULDC: districts Planning and Land Development Regulation Act) and zoning the general powers confirmed in F.S. Ch. 166 (Home A. -

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -

Useful Forestry Measurements Acre: a Unit of Area Equaling 43,560
Useful Forestry Measurements Acre: A unit of area equaling 43,560 square feet or 10 square chains. Basal Area: The area, usually in square feet, of the cross-section of a tree stem near its base, generally at breast height and inclusive of bark. The basal area per acre measurement gives you some idea of crowding of trees in a stand. Board Foot: A unit of area for measuring lumber equaling 12 inches by 12 inches by 1 inch. Chain: A unit of length. A surveyor’s chain equals 66 feet or 1/80-mile. Cord: A pile of stacked wood measuring 4 feet by 4 feet by 8 feet when originally conceived. Cubic Foot: A unit of volume measure, wood equivalent to a solid cube that measures 12 inches by 12 inches by 12 inches or 1,728 cubic inches. Cunit: A volume of wood measuring 3 feet and 1-1/2 inches by 4 feet by 8 feet and containing 100 solid cubic feet of wood. D.B.H. (diameter breast height): The measurement of a tree’s diameter at 4-1/2 feet above the ground line. M.B.F. (thousand board feet): A unit of measure containing 1,000 board feet. Section: A unit of area containing 640 acres or one square mile. Square Foot: A unit of area equaling 144 square inches. Township: A unit of land area covering 23,040 acres or 36 sections. Equations Cords per acre (based on 10 Basal Area Factor (BAF) angle gauge) (# of 8 ft sticks + # of trees)/(2 x # plots) Based on 10 Basal Area Factor Angle Gauge Example: (217+30)/(2 x 5) = 24.7 cords/acre BF per acre ((# of 8 ft logs + # of trees)/(2 x # plots)) x 500 Bd ft Example: (((150x2)+30)/(2x5))x500 = 9000 BF/acre or -

Colorado Metric Conversion Manual
COLORADO OT . DEPARTMENT OF TRANSPORTATION METRIC CONVERSION MANUAL January 1994 This manual or any part thereof must not be reproduced in any form without the following disclaimer. The information presented in this publication haS been prepared in accordance with recognized engineering principles and is for general information only. While it is believed to be accurate, this information should not be used or relied upon for any specific application without competent professional examination and verification of its accuracy, suitability, and applicability by a competent licensed engineer or other licensed professional. Publication of the material contained herein is not intended as a representation or warranty on the part of the Colorado Department of Transportation (CDOT) , that this information is suitable for any general or particular use or of freedom from infringement of any patent or patents. Anyone making use of this information assumes all liability arising from such use. Caution must be exercised when relying upon the specifications and codes developed by other bodies and incorporated herein, since such material may be modified or amended from time to time subsequent to the printing of this edition. COOT bears no responsibility for such material other than to incorporate it at the time of the initial publication of this edition, subject to the general comments set forth in the preceding paragraph. Table of Contents Preface ................................................... v Introduction . vii Chapter 1: Metric Units, Terms, Symbols, and Conversion Factors . ... 1-1 Basic Metric . 1-1 Length, Area, Volume and Temperature . 1-7 Civil and Structural Engineering . 1-10 Metric Project Definition ....................... .. 1-12 Chapter 2: Right-Of-Way ................................... -

Metric System Conversion Factors1 J
AGR39 Metric System Conversion Factors1 J. Bryan Unruh, Barry J. Brecke, and Ramon G. Leon-Gonzalez2 Area Equivalents 1 Hectare (ha) 2 1 Acre (A) = 10,000 square meters (m ) 2 = 100 are (a) = 43,560 square feet (ft ) = 2.471 acres (A) = 4,840 square yards (yd2) = 0.405 hectares (ha) 1 Square Foot (ft) = 160 square rods (rd2) 2 = 4,047 square meters (m2) = 144 square inches (in ) = 929.03 square centimeters (cm2) 2 1 Acre-inch (ac-in) = 0.0929 square meters (m ) 3 = 102.8 cubic meters (m ) 1 Square Mile (mi) = 27,154 gallons, US (gal) 2 = 3,630 cubic feet (ft3) = 27,878,400 square feet (ft ) = 3,097,600 square yards (yd2) 2 1 Are (a) = 640 square acres (A ) = 2,589,988.11 square meters (m2) = 100 square meters (m2) 2 = 119.6 square yards (yd ) 1 Square Rod (rd) = 0.025 acre (A) = 39,204 square inches (in2) = 272.25 square feet (ft2) 1 Cubic Foot (ft) 2 3 = 30.25 square yards (yds ) = 1,728 cubic inches (in ) = 25.3 square meters (m2) = 0.037 cubic yards (yds3) 3 = 0.02832 cubic meters (cm ) 1 Square Yard (yd) = 28,320 cubic centimeters (cm3) = 9 square feet (ft2) 2 1 Cubic Yard (yd) = 0.836 square meters (m ) = 27 cubic feet (ft3) = 0.764 cubic meters (m3) 1. This document is AGR39, one of a series of the Environmental Horticulture Department, UF/IFAS Extension. Original publication date November 1993. Revised December 2014. Reviewed December 2017. Visit the EDIS website at http://edis.ifas.ufl.edu. -

Map Projections
Map Projections Chapter 4 Map Projections What is map projection? Why are map projections drawn? What are the different types of projections? Which projection is most suitably used for which area? In this chapter, we will seek the answers of such essential questions. MAP PROJECTION Map projection is the method of transferring the graticule of latitude and longitude on a plane surface. It can also be defined as the transformation of spherical network of parallels and meridians on a plane surface. As you know that, the earth on which we live in is not flat. It is geoid in shape like a sphere. A globe is the best model of the earth. Due to this property of the globe, the shape and sizes of the continents and oceans are accurately shown on it. It also shows the directions and distances very accurately. The globe is divided into various segments by the lines of latitude and longitude. The horizontal lines represent the parallels of latitude and the vertical lines represent the meridians of the longitude. The network of parallels and meridians is called graticule. This network facilitates drawing of maps. Drawing of the graticule on a flat surface is called projection. But a globe has many limitations. It is expensive. It can neither be carried everywhere easily nor can a minor detail be shown on it. Besides, on the globe the meridians are semi-circles and the parallels 35 are circles. When they are transferred on a plane surface, they become intersecting straight lines or curved lines. 2021-22 Practical Work in Geography NEED FOR MAP PROJECTION The need for a map projection mainly arises to have a detailed study of a 36 region, which is not possible to do from a globe. -

How to Determine Latitude and Longitude from Topographic Maps
Oregon Department of Environmental Quality HOW TO DETERMINE LATITUDE AND LONGITUDE FROM TOPOGRAPHIC MAPS Latitude is the distance north or south of the equator. 2. For each location, construct a small rectangle around Longitude is the distance east or west of the prime the point with fine pencil lines connecting the nearest meridian (Greenwich, England). Latitude and longitude 2-1/2′ or 5′ graticules. Graticules are intersections of are measured in seconds, minutes, and degrees: latitude and longitude lines that are marked on the map edge, and appear as black crosses at four points in ″ ′ 60 (seconds) = 1 (minute) the interior of the map. 60′ (minutes) = 1° (degree) 3. Read and record the latitude and longitude for the To determine the latitude and longitude of your facility, southeast corner of the small quadrangle drawn in step you will need a topographic map from United States two. The latitude and longitude are printed at the edges Geological Survey (USGS). of the map. How to Obtain USGS Maps: 4. To determine the increment of latitude above the latitude line recorded in step 3: USGS maps used for determining latitude and longitude • Position the map so that you face its west edge; may be obtained from the USGS distribution center. These maps are available in both the 7.5 minute and l5 • Place the ruler in approximately a north-south minute series. For maps of the United States, including alignment, with the “0” on the latitude line recorded Alaska, Hawaii, American Samoa, Guam, Puerto Rico, in step 3 and the edge intersecting the point. -

Calculating the Surface Area of Your Landscape
Tips for Calculating Surface Area Area is defined in terms of square measures. The most commonly used area measurements are square feet and acres. Areas of : rectangle or square = length x width trapezoid = parallel sides A + B / 2 x height triangle = base x height / 2 circle = radius (1/2 diameter) squared x 3.14 oval = length x width x 0.8 The offset method is used to measure the area (square feet) of irregularly shaped areas. It reduces large areas to a series of smaller trapezoids that are equally spaced along a measured line. This method will determine the area to within 5%. The four steps in determining area by the offset method are as follows: Step 1: Determine the length line. This is the longest axis of the figure. Its endpoints should be labeled A and B. A B Step 2: Mark offset lines at right angles to the length line. Choose how many offset lines to use so that they divide line AB into equal segments and define regions amenable to calculation. For example, if the length line is 40 feet, a logical distance between offset lines would be 10 feet, which would end up with 4 measurements. If the shape of the area is uniform, fewer offset lines are needed. However, if the shape is irregular, more offset lines are needed. A B 10 ft. Step 3: Measure the length of each offset line. These are measured from one edge of the area to the other. A B 10 ft. 15 ft. 12 ft. 5 ft. Step 4: Add up the lengths of all offset lines and multiply by the distance between offset lines on the length line. -
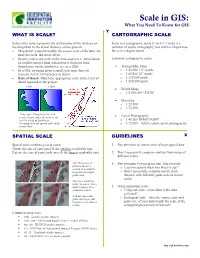
Scale in GIS: What You Need to Know for GIS
Scale in GIS: What You Need To Know for GIS Y WHAT IS SCALE? CARTOGRAPHIC SCALE Scale is the scale represents the relationship of the distance on Scale in a cartographic sense (1 inch = 1 mile) is a the map/data to the actual distance on the ground. remnant of vector cartography, but still has importance • Map detail is determined by the source scale of the data: the for us in a digital world. finer the scale, the more detail. • Source scale is the scale of the data source (i.e. aerial photo Common cartographic scales: or satellite image) from which data is digitized (into boundaries, roads, landcover, etc. in a GIS). • Topographic Maps • In a GIS, zooming in on a small scale map does not o 1:24,000 7.5” quads increase its level of accuracy or detail. o 1:63,360 15” quads • Rule of thumb: Match the appropriate scale to the level of o 1:100,000 quads detail required in the project. o 1:250,000 quads 1:500 1:1200 • World Maps o 1:2,000,000 – DCW • Shoreline o 1:20,000 o 1:70,000 Above, right. Comparing fine and coarse source scales shows how the • Aerial Photography level of detail in the data is o 1:40,000 NHAP/NAPP determined by the spatial scale of the o 1:12,000 – 4,000 custom aerial photography source data. SPATIAL SCALE GUIDELINES X Spatial scale involves grain & extent: 1. Pay attention to source scale of your spatial data. Grain: the size of your pixel & the smallest resolvable unit.