A New Approach to Galaxy Structural Analysis with the Curvature of the Brightness Pro Le
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Li Abundances in F Stars: Planets, Rotation, and Galactic Evolution�,
A&A 576, A69 (2015) Astronomy DOI: 10.1051/0004-6361/201425433 & c ESO 2015 Astrophysics Li abundances in F stars: planets, rotation, and Galactic evolution, E. Delgado Mena1,2, S. Bertrán de Lis3,4, V. Zh. Adibekyan1,2,S.G.Sousa1,2,P.Figueira1,2, A. Mortier6, J. I. González Hernández3,4,M.Tsantaki1,2,3, G. Israelian3,4, and N. C. Santos1,2,5 1 Centro de Astrofisica, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal e-mail: [email protected] 2 Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal 3 Instituto de Astrofísica de Canarias, C/via Lactea, s/n, 38200 La Laguna, Tenerife, Spain 4 Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain 5 Departamento de Física e Astronomía, Faculdade de Ciências, Universidade do Porto, Portugal 6 SUPA, School of Physics and Astronomy, University of St. Andrews, St. Andrews KY16 9SS, UK Received 28 November 2014 / Accepted 14 December 2014 ABSTRACT Aims. We aim, on the one hand, to study the possible differences of Li abundances between planet hosts and stars without detected planets at effective temperatures hotter than the Sun, and on the other hand, to explore the Li dip and the evolution of Li at high metallicities. Methods. We present lithium abundances for 353 main sequence stars with and without planets in the Teff range 5900–7200 K. We observed 265 stars of our sample with HARPS spectrograph during different planets search programs. We observed the remaining targets with a variety of high-resolution spectrographs. -

195 9Apj. . .130. .629B the HERCULES CLUSTER OF
.629B THE HERCULES CLUSTER OF NEBULAE* .130. G. R. Burbidge and E. Margaret Burbidge 9ApJ. Yerkes and McDonald Observatories Received March 26, 1959 195 ABSTRACT The northern of two clusters of nebulae in Hercules, first listed by Shapley in 1933, is an irregular group of about 75 bright nebulae and a larger number of faint ones, distributed over an area about Io X 40'. A set of plates of parts of this cluster, taken by Dr. Walter Baade with the 200-inch Hale reflector, is shown and described. More than three-quarters of the bright nebulae have been classified, and, of these, 69 per cent are spirals or irregulars and 31 per cent elliptical or SO. Radial velocities for 7 nebulae were obtained by Humason, and 10 have been obtained by us with the 82-inch reflector. The mean red shift is 10775 km/sec. From this sample, the total kinetic energy of the nebulae has been esti- mated. By measuring the distances between all pairs on a 48-inch Schmidt enlargement, the total poten- tial energy has been estimated. From these results it is concluded that, if the cluster is to be in a stationary state, the average galactic mass must be ^1012Mo. Three possibilities are discussed: that the masses are indeed as large as this, that there is a large amount of intergalactic matter, and that the cluster is expanding. The data for the Coma and Virgo clusters are also reviewed. It is concluded that both the Hercules and the Virgo clusters are probably expanding, but the situation is uncertain in the case of the Coma cluster. -

7.5 X 11.5.Threelines.P65
Cambridge University Press 978-0-521-19267-5 - Observing and Cataloguing Nebulae and Star Clusters: From Herschel to Dreyer’s New General Catalogue Wolfgang Steinicke Index More information Name index The dates of birth and death, if available, for all 545 people (astronomers, telescope makers etc.) listed here are given. The data are mainly taken from the standard work Biographischer Index der Astronomie (Dick, Brüggenthies 2005). Some information has been added by the author (this especially concerns living twentieth-century astronomers). Members of the families of Dreyer, Lord Rosse and other astronomers (as mentioned in the text) are not listed. For obituaries see the references; compare also the compilations presented by Newcomb–Engelmann (Kempf 1911), Mädler (1873), Bode (1813) and Rudolf Wolf (1890). Markings: bold = portrait; underline = short biography. Abbe, Cleveland (1838–1916), 222–23, As-Sufi, Abd-al-Rahman (903–986), 164, 183, 229, 256, 271, 295, 338–42, 466 15–16, 167, 441–42, 446, 449–50, 455, 344, 346, 348, 360, 364, 367, 369, 393, Abell, George Ogden (1927–1983), 47, 475, 516 395, 395, 396–404, 406, 410, 415, 248 Austin, Edward P. (1843–1906), 6, 82, 423–24, 436, 441, 446, 448, 450, 455, Abbott, Francis Preserved (1799–1883), 335, 337, 446, 450 458–59, 461–63, 470, 477, 481, 483, 517–19 Auwers, Georg Friedrich Julius Arthur v. 505–11, 513–14, 517, 520, 526, 533, Abney, William (1843–1920), 360 (1838–1915), 7, 10, 12, 14–15, 26–27, 540–42, 548–61 Adams, John Couch (1819–1892), 122, 47, 50–51, 61, 65, 68–69, 88, 92–93, -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

XID: Cross-Association of ROSAT/Bright Source Catalog X
THE ASTROPHYSICAL JOURNAL SUPPLEMENT SERIES, 131:335È353, 2000 November ( 2000. The American Astronomical Society. All rights reserved. Printed in U.S.A. XID: CROSS-ASSOCIATION OF ROSAT /BRIGHT SOURCE CATALOG X-RAY SOURCES WITH USNO A-2 OPTICAL POINT SOURCES ROBERT E. RUTLEDGE,ROBERT J. BRUNNER, AND THOMAS A. PRINCE Division of Physics, Mathematics and Astronomy, MS 220-47, California Institute of Technology, Pasadena, CA 91107; rutledge=srl.caltech.edu, rb=astro.caltech.edu, prince=srl.caltech.edu AND CAROL LONSDALE Infrared Processing and Analysis Center, Caltech/JPL, Pasadena, CA 91125; cjl=ipac.caltech.edu Received 1999 December 8; accepted 2000 April 4 ABSTRACT We quantitatively cross-associate the 18,811 ROSAT Bright Source Catalog (RASS/BSC) X-ray sources with optical sources in the USNO A-2 catalog, calculating the probability of unique association (P ) between each candidate within 75A of the X-ray source position, on the basis of optical magnitude id [ [ [ and proximity. We present catalogs of RASS/BSC sources for whichPid 98%, Pid 90%, and Pid 50%, which contain 2705, 5492, and 11,301 unique USNO A-2 optical counterparts respectively down to the stated level of signiÐcance. Together with identiÐcations of objects not cataloged in USNO A-2 due to their high surface brightness (M31, M32, . .) and optical pairs, we produced a total of 11,803 associ- [ ations to a probability ofPid 50%. We include in this catalog a list of objects in the SIMBAD data- base within 10A of the USNO A-2 position, as an aid to identiÐcation and source classiÐcation. This is the Ðrst RASS/BSC counterpart catalog which provides a probability of association between each X-ray source and counterpart, quantifying the certainty of each individual association. -
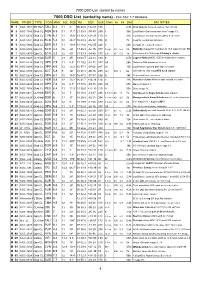
DSO List V2 Current
7000 DSO List (sorted by name) 7000 DSO List (sorted by name) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs Dist SAC NOTES M 1 NGC 1952 SN Rem TAU 8.4 11 8' 05 34.5 +22 01 135 6.3k Crab Nebula; filaments;pulsar 16m;3C144 M 2 NGC 7089 Glob CL AQR 6.5 11 11.7' 21 33.5 -00 49 255 II 36k Lord Rosse-Dark area near core;* mags 13... M 3 NGC 5272 Glob CL CVN 6.3 11 18.6' 13 42.2 +28 23 110 VI 31k Lord Rosse-sev dark marks within 5' of center M 4 NGC 6121 Glob CL SCO 5.4 12 26.3' 16 23.6 -26 32 336 IX 7k Look for central bar structure M 5 NGC 5904 Glob CL SER 5.7 11 19.9' 15 18.6 +02 05 244 V 23k st mags 11...;superb cluster M 6 NGC 6405 Opn CL SCO 4.2 10 20' 17 40.3 -32 15 377 III 2 p 80 6.2 2k Butterfly cluster;51 members to 10.5 mag incl var* BM Sco M 7 NGC 6475 Opn CL SCO 3.3 12 80' 17 53.9 -34 48 377 II 2 r 80 5.6 1k 80 members to 10th mag; Ptolemy's cluster M 8 NGC 6523 CL+Neb SGR 5 13 45' 18 03.7 -24 23 339 E 6.5k Lagoon Nebula;NGC 6530 invl;dark lane crosses M 9 NGC 6333 Glob CL OPH 7.9 11 5.5' 17 19.2 -18 31 337 VIII 26k Dark neb B64 prominent to west M 10 NGC 6254 Glob CL OPH 6.6 12 12.2' 16 57.1 -04 06 247 VII 13k Lord Rosse reported dark lane in cluster M 11 NGC 6705 Opn CL SCT 5.8 9 14' 18 51.1 -06 16 295 I 2 r 500 8 6k 500 stars to 14th mag;Wild duck cluster M 12 NGC 6218 Glob CL OPH 6.1 12 14.5' 16 47.2 -01 57 246 IX 18k Somewhat loose structure M 13 NGC 6205 Glob CL HER 5.8 12 23.2' 16 41.7 +36 28 114 V 22k Hercules cluster;Messier said nebula, no stars M 14 NGC 6402 Glob CL OPH 7.6 12 6.7' 17 37.6 -03 15 248 VIII 27k Many vF stars 14.. -

DSO List V2 Current
7000 DSO List (sorted by constellation - magnitude) 7000 DSO List (sorted by constellation - magnitude) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs SAC NOTES M 31 NGC 224 Galaxy AND 3.4 13.5 189' 00 42.7 +41 16 60 Sb Andromeda Galaxy;Local Group;nearest spiral NGC 7686 OCL 251 Opn CL AND 5.6 - 15' 23 30.1 +49 08 88 IV 1 p 20 6.2 H VIII 69;12* mags 8...13 NGC 752 OCL 363 Opn CL AND 5.7 - 50' 01 57.7 +37 40 92 III 1 m 60 9 H VII 32;Best in RFT or binocs;Ir scattered cl 70* m 8... M 32 NGC 221 Galaxy AND 8.1 12.4 8.5' 00 42.7 +40 52 60 E2 Companion to M31; Member of Local Group M 110 NGC 205 Galaxy AND 8.1 14 19.5' 00 40.4 +41 41 60 SA0 M31 Companion;UGC 426; Member Local Group NGC 272 OCL 312 Opn CL AND 8.5 - 00 51.4 +35 49 90 IV 1 p 8 9 NGC 7662 PK 106-17.1 Pln Neb AND 8.6 5.6 17'' 23 25.9 +42 32 88 4(3) 14 Blue Snowball Nebula;H IV 18;Barnard-cent * variable? NGC 956 OCL 377 Opn CL AND 8.9 - 8' 02 32.5 +44 36 62 IV 1 p 30 9 NGC 891 UGC 1831 Galaxy AND 9.9 13.6 13.1' 02 22.6 +42 21 62 Sb NGC 1023 group;Lord Rosse drawing shows dark lane NGC 404 UGC 718 Galaxy AND 10.3 12.8 4.3' 01 09.4 +35 43 91 E0 Mirach's ghost H II 224;UGC 718;Beta AND sf 6' IC 239 UGC 2080 Galaxy AND 11.1 14.2 4.6' 02 36.5 +38 58 93 SBa In NGC 1023 group;vsBN in smooth bar;low surface br NGC 812 UGC 1598 Galaxy AND 11.2 12.8 3' 02 06.9 +44 34 62 Sbc Peculiar NGC 7640 UGC 12554 Galaxy AND 11.3 14.5 10' 23 22.1 +40 51 88 SBbc H II 600;nearly edge on spiral MCG +08-01-016 Galaxy AND 12 - 1.0' 23 59.2 +46 53 59 Face On MCG +08-01-018 -

Her – Objektauswahl NGC Teil 1
Her – Objektauswahl NGC Teil 1 NGC 6013 NGC 6044 NGC 6060 NGC 6098 NGC 6149 NGC 6166 NGC 6185 NGC 6210 NGC 6028 NGC 6045 NGC 6061 NGC 6099 NGC 6150 NGC 6168 NGC 6186 NGC 6212 NGC 6030 NGC 6047 NGC 6062 NGC 6106 NGC 6154 NGC 6173 NGC 6194 NGC 6219 NGC 6032 NGC 6050 NGC 6073 NGC 6113 NGC 6155 NGC 6174 NGC 6195 NGC 6224 Teil 2 NGC 6034 NGC 6052 NGC 6074 NGC 6132 NGC 6158 NGC 6175 NGC 6196 NGC 6225 Teil 3 NGC 6035 NGC 6054 NGC 6075 NGC 6141 NGC 6159 NGC 6177 NGC 6197 NGC 6228 NGC 6040 NGC 6055 NGC 6078 NGC 6145 NGC 6160 NGC 6179 NGC 6201 NGC 6229 NGC 6041 NGC 6056 NGC 6081 NGC 6146 NGC 6161 NGC 6180 NGC 6203 NGC 6230 NGC 6042 NGC 6057 NGC 6083 NGC 6147 NGC 6162 NGC 6181 NGC 6205 NGC 6233 NGC 6043 NGC 6058 NGC 6084 NGC 6148 NGC 6163 NGC 6184 NGC 6207 NGC 6239 Zur Objektauswahl: Nummer anklicken Sternbild- Zur Übersichtskarte: Objekt in Aufsuchkarte anklicken Übersicht Zum Detailfoto: Objekt in Übersichtskarte anklicken Her – Objektauswahl NGC Teil 2 NGC 6241 NGC 6270 NGC 6308 NGC 6329 NGC 6350 NGC 6389 NGC 6447 NGC 6490 NGC 6243 NGC 6271 NGC 6311 NGC 6330 NGC 6351 NGC 6408 NGC 6452 NGC 6495 Teil 1 NGC 6255 NGC 6272 NGC 6312 NGC 6332 NGC 6363 NGC 6417 NGC 6458 NGC 6500 NGC 6257 NGC 6274 NGC 6313 NGC 6336 NGC 6364 NGC 6427 NGC 6460 NGC 6501 NGC 6261 NGC 6276 NGC 6314 NGC 6339 NGC 6367 NGC 6429 NGC 6467 NGC 6504 Teil 3 NGC 6263 NGC 6278 NGC 6315 NGC 6341 NGC 6371 NGC 6430 NGC 6482 NGC 6513 NGC 6264 NGC 6279 NGC 6320 NGC 6343 NGC 6372 NGC 6433 NGC 6484 NGC 6518 NGC 6265 NGC 6282 NGC 6321 NGC 6347 NGC 6375 NGC 6442 NGC 6485 NGC 6524 NGC 6267 NGC -

Kataloge Von Abell, Arp, Hickson Und Co
Kataloge von Abell, Arp, Hickson und Co. Ein astronomischer Katalog ist ein Verzeichnis astronomischer Objekte mit gemeinsamen Eigenschaften, etwa Form, Zusammensetzung oder ihre Entdeckungs- methode. Astronomische Kataloge sind meistens das Ergebnis von Untersuchungen zu astronomischen Objekten Kataloge für Objekte des Sonnensystems ( Planeten, Asteroiden, Kometen, Kleinplaneten) Stellare Einzelobjekte (Sterne, Exoplaneten, Pulsare u. a.) z.B. GSC (25 Millionen), HIP (>1 Million), Kepler (>500) Kataloge für Sternhaufen Cr (Collinder Katalog, Per Collinder, 1931) 471 offene Sternhaufen GCL (Globular Clusters, Alter G., Ruprecht J., Vanysek V. 1970 ) 137 Kugelsternhaufen OCL (Alter G., Ruprecht J., Vanysek V. 1983 ) 1112 offene Sternhaufen Tr (Trumpler Katalog ; Robert Julius Trumpler, 1930 ) 37 offene Sternhaufen Interstellare Materie Diffuse und planetarische Nebel, Dunkelwolken, Molekülwolken, SN-Reste B (Barnard-Katalog, Edward Barnard; 1927) 349 CED (Catalog of bright diffuse Galactic nebulae, Cederblad 1946) 330 LBN (Lynds´ Catalogue of Bright Nebulae, B.T. Lynds; 1965) 1125 LDN (Lynds´ Catalogue of Dark Nebulae, B.T. Lynds; 1962) 1791 Sh (Catalogue of HII Regions, Sharpless S. , 1959) 313 VdB (Catalogue of Reflection Nebulae; Sidney van den Bergh; 1966) 158 Extragalaktische Objekte (Galaxien, Galaxienhaufen, Quasare) Abell ( Katalog der Galaxienhaufen, George Ogden Abell, 1958, 1989) 4073 Arp ( Atlas of Peculiar Galaxies, Halton C. Arp, 1966) 338 AM ( Southern Peculiar Galaxies; Arp, Barry F. Madore, 1987) 6445 CGCG -
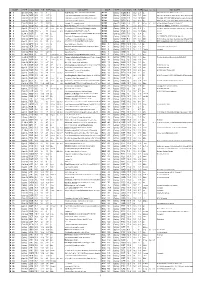
7000 List by Name
NAME TYPE CON MAG S.B. SIZE Class ns bs SAC NOTES NAME TYPE CON MAG S.B. SIZE Class ns bs SAC NOTES M 1 SN Rem TAU 8.4 11 8' Crab Nebula; filaments;pulsar 16m;3C144 -M 99 Galaxy COM 9.9 13.2 5.3' Sc SN 1967h;Norton-diff for small scope M 2 Glob CL AQR 6.5 11 11.7' II Lord Rosse-Dark area near core;* mags 13... -M 100 Galaxy COM 9.4 13.4 7.5' SBbc SN 1901-14-59;NGC 4322 @ 5.2';NGC 4328 @ 6.1' M 3 Glob CL CVN 6.3 11 18.6' VI Lord Rosse-sev dark marks within 5' of center -M 101 Galaxy UMA 7.9 14.9 28.5' SBc P w NGC 5474;SN 1909;spir galax w one heavy arm; M 4 Glob CL SCO 5.4 12 26.3' IX Look for central bar structure -M 102 Galaxy DRA 9.9 12.2 6.5' Sa vBN w dk lane and ansae;NGC 5867 small E neb; M 5 Glob CL SER 5.7 11 19.9' V st mags 11...;superb cluster -M 103 Opn CL CAS 7.4 11 6' III 2 p 40 10.6 in Cas OB8;incl Struve 131 6-9m 14'' M 6 Opn CL SCO 4.2 10 20' III 2 p 80 6.2 Butterfly cluster;51 members to 10.5 mag incl var*- BMM104 Sco Galaxy VIR 8 11.6 8.6' Sab Sombrero Galaxy; H I 43;dark equatorial lane; M 7 Opn CL SCO 3.3 12 80' II 2 r 80 5.6 80 members to 10th mag; Ptolemy's cluster -M 105 Galaxy LEO 9.3 12.8 5.3' E1 P w NGC 3384 @ 7.2';NGC 3389 @ 10 ';Leo Group M 8 Opn CL SGR 4.6 - 15' II 2 m n 6.9 In Lagoon nebula M8;25* mags 7..