DOCSLIB.ORG

CSE 326: Data Structures Binary Search Trees

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
CSE 326: Data Structures Binary Search Trees Announcements (1/23/09) CSE 326: Data Structures • HW #2 due now • HW #3 out today, due at beginning of class next Binary Search Trees Friday. • Project 2A due next Wed. night. Steve Seitz Winter 2009 • Read Chapter 4 1 2 ADTs Seen So Far The Dictionary ADT • seitz •Data: Steve • Stack •Priority Queue Seitz –a set of insert(seitz, ….) CSE 592 –Push –Insert (key, value) pairs –Pop – DeleteMin •ericm6 Eric • Operations: McCambridge – Insert (key, value) CSE 218 •Queue find(ericm6) – Find (key) • ericm6 • soyoung – Enqueue Then there is decreaseKey… Eric, McCambridge,… – Remove (key) Soyoung Shin – Dequeue CSE 002 •… The Dictionary ADT is also 3 called the “Map ADT” 4 A Modest Few Uses Implementations insert find delete •Sets • Unsorted Linked-list • Dictionaries • Networks : Router tables • Operating systems : Page tables • Unsorted array • Compilers : Symbol tables • Sorted array Probably the most widely used ADT! 5 6 Binary Trees Binary Tree: Representation • Binary tree is A – a root left right – left subtree (maybe empty) A pointerpointer A – right subtree (maybe empty) B C B C B C • Representation: left right left right pointerpointer pointerpointer D E F D E F Data left right G H D E F pointer pointer left right left right left right pointerpointer pointerpointer pointerpointer I J 7 8 Tree Traversals Inorder Traversal void traverse(BNode t){ A traversal is an order for if (t != NULL) visiting all the nodes of a tree + traverse (t.left); process t.element; Three types: * 5 traverse (t.right); • Pre-order: Root, left subtree, right subtree 2 4 } • In-order: Left subtree, root, right subtree } (an expression tree) • Post-order: Left subtree, right subtree, root 9 10 Binary Tree: Special Cases Binary Tree: Some Numbers… Recall: height of a tree = longest path from root to leaf. A A A A For binary tree of height h: – max # of leaves: B C B C B C B – max # of nodes: D E F D E F G D E F G C Complete Tree Perfect Tree “List” Tree – min # of leaves: H I Full Tree – min # of nodes: 11 12 Binary Tree: Some Numbers… Binary Search Tree Data Structure Recall: depth of a node = path length from node to root. • Structural property – each node has ≤ 2children Consider the space of all possible binary trees of N nodes. – result: 8 • Sum up the depths of every node in that forest and divide by • storage is small the number of nodes. • operations are simple • This is the average depth over all nodes over all binary trees of 5 11 size N. How big is it? • Order property – all keys in left subtree smaller 2 6 10 12 than root’s key What would the average depth be for a well-balanced tree? – all keys in right subtree larger than root’s key 4 7 9 14 – result: easy to find any given key 13 13 14 Example and Counter-Example Find in BST, Recursive Node Find(Object key, 12 Node root) { 5 8 if (root == NULL) return NULL; 5 15 4 8 5 11 if (key < root.key) 2 9 20 return Find(key, root.left); 1 7 11 2 7 6 10 18 else if (key > root.key) 7 10 17 30 return Find(key, root.right); 3 4 15 20 else return root; Runtime: } BINARY SEARCH TREES? 21 15 16 Find in BST, Iterative Bonus: FindMin/FindMax Node Find(Object key, Node root) { • Find minimum 12 12 while (root != NULL && root.key != key) { if (key < root.key) 5 15 5 15 root = root.left; • Find maximum else 2 9 20 2 9 20 root = root.right; } 7 10 17 30 7 10 17 30 return root; } Runtime: 17 18 Insert in BST BuildTree for BST 12 • Suppose keys 1, 2, 3, 4, 5, 6, 7, 8, 9 are inserted into Insert(13) an initially empty BST. 5 15 Insert(8) Insert(31) If inserted in given order, what is the tree? What big-O 2 9 20 runtime for this kind of sorted input? 7 10 17 30 Insertions happen only at the leaves – easy! If inserted in reverse order, Runtime: what is the tree? What big-O runtime for this kind of 19 sorted input? 20 BuildTree for BST Deletion in BST • Suppose keys 1, 2, 3, 4, 5, 6, 7, 8, 9 are inserted into 12 an initially empty BST. 5 15 – If inserted median first, then left median, right median, etc., what is the tree? What is the big-O runtime for this kind of sorted input? 2 9 20 7 10 17 30 Why might deletion be harder than insertion? 21 22 Deletion Deletion – The Leaf Case • Removing an item disrupts the tree structure. • Basic idea: find the node that is to be removed. 12 Then “fix” the tree so that it is still a binary search Delete(17) tree. 5 15 • Three cases: – node has no children (leaf node) 2 9 20 – node has one child – node has two children 7 10 17 30 23 24 Deletion – The One Child Case Deletion – The Two Child Case 12 Delete(15) 12 Delete(5) 5 20 5 15 2 9 30 2 9 20 7 10 7 10 30 What can we replace 5 with? 25 26 Deletion – The Two Child Case Finally… Idea: Replace the deleted node with a value guaranteed to be between the two child subtrees 12 7 replaces 5 Options: 7 20 • succ from right subtree: findMin(t.right) • pred from left subtree : findMax(t.left) 2 9 30 10 Now delete the original node containing succ or pred • Leaf or one child case – easy! Original node containing 7 gets deleted 27 28 Balanced BST Observations • BST: the shallower the better! • For a BST with n nodes – Average depth (averaged over all possible insertion orderings) is O(log n) – Worst case maximum depth is O(n) • Simple cases such as insert(1, 2, 3, ..., n) lead to the worst case scenario Solution: Require a Balance Condition that 1. ensures depth is O(log n) – strong enough! 2. is easy to maintain – not too strong! 29.
Load more

Recommended publications
  • Assignment 3: Kdtree ______Due June 4, 11:59 PM
    CS106L Handout #04 Spring 2014 May 15, 2014 Assignment 3: KDTree _________________________________________________________________________________________________________ Due June 4, 11:59 PM Over the past seven weeks, we've explored a wide array of STL container classes. You've seen the linear vector and deque, along with the associative map and set. One property common to all these containers is that they are exact. An element is either in a set or it isn't. A value either ap- pears at a particular position in a vector or it does not. For most applications, this is exactly what we want. However, in some cases we may be interested not in the question “is X in this container,” but rather “what value in the container is X most similar to?” Queries of this sort often arise in data mining, machine learning, and computational geometry. In this assignment, you will implement a special data structure called a kd-tree (short for “k-dimensional tree”) that efficiently supports this operation. At a high level, a kd-tree is a generalization of a binary search tree that stores points in k-dimen- sional space. That is, you could use a kd-tree to store a collection of points in the Cartesian plane, in three-dimensional space, etc. You could also use a kd-tree to store biometric data, for example, by representing the data as an ordered tuple, perhaps (height, weight, blood pressure, cholesterol). However, a kd-tree cannot be used to store collections of other data types, such as strings. Also note that while it's possible to build a kd-tree to hold data of any dimension, all of the data stored in a kd-tree must have the same dimension.
    [Show full text]
  • Binary Search Tree
    ADT Binary Search Tree! Ellen Walker! CPSC 201 Data Structures! Hiram College! Binary Search Tree! •" Value-based storage of information! –" Data is stored in order! –" Data can be retrieved by value efficiently! •" Is a binary tree! –" Everything in left subtree is < root! –" Everything in right subtree is >root! –" Both left and right subtrees are also BST#s! Operations on BST! •" Some can be inherited from binary tree! –" Constructor (for empty tree)! –" Inorder, Preorder, and Postorder traversal! •" Some must be defined ! –" Insert item! –" Delete item! –" Retrieve item! The Node<E> Class! •" Just as for a linked list, a node consists of a data part and links to successor nodes! •" The data part is a reference to type E! •" A binary tree node must have links to both its left and right subtrees! The BinaryTree<E> Class! The BinaryTree<E> Class (continued)! Overview of a Binary Search Tree! •" Binary search tree definition! –" A set of nodes T is a binary search tree if either of the following is true! •" T is empty! •" Its root has two subtrees such that each is a binary search tree and the value in the root is greater than all values of the left subtree but less than all values in the right subtree! Overview of a Binary Search Tree (continued)! Searching a Binary Tree! Class TreeSet and Interface Search Tree! BinarySearchTree Class! BST Algorithms! •" Search! •" Insert! •" Delete! •" Print values in order! –" We already know this, it#s inorder traversal! –" That#s why it#s called “in order”! Searching the Binary Tree! •" If the tree is
    [Show full text]
  • Search Trees for Strings a Balanced Binary Search Tree Is a Powerful Data Structure That Stores a Set of Objects and Supports Many Operations Including
    Search Trees for Strings A balanced binary search tree is a powerful data structure that stores a set of objects and supports many operations including: Insert and Delete. Lookup: Find if a given object is in the set, and if it is, possibly return some data associated with the object. Range query: Find all objects in a given range. The time complexity of the operations for a set of size n is O(log n) (plus the size of the result) assuming constant time comparisons. There are also alternative data structures, particularly if we do not need to support all operations: • A hash table supports operations in constant time but does not support range queries. • An ordered array is simpler, faster and more space efficient in practice, but does not support insertions and deletions. A data structure is called dynamic if it supports insertions and deletions and static if not. 107 When the objects are strings, operations slow down: • Comparison are slower. For example, the average case time complexity is O(log n logσ n) for operations in a binary search tree storing a random set of strings. • Computing a hash function is slower too. For a string set R, there are also new types of queries: Lcp query: What is the length of the longest prefix of the query string S that is also a prefix of some string in R. Prefix query: Find all strings in R that have S as a prefix. The prefix query is a special type of range query. 108 Trie A trie is a rooted tree with the following properties: • Edges are labelled with symbols from an alphabet Σ.
    [Show full text]
  • Trees, Binary Search Trees, Heaps & Applications Dr. Chris Bourke
    Trees Trees, Binary Search Trees, Heaps & Applications Dr. Chris Bourke Department of Computer Science & Engineering University of Nebraska|Lincoln Lincoln, NE 68588, USA [email protected] http://cse.unl.edu/~cbourke 2015/01/31 21:05:31 Abstract These are lecture notes used in CSCE 156 (Computer Science II), CSCE 235 (Dis- crete Structures) and CSCE 310 (Data Structures & Algorithms) at the University of Nebraska|Lincoln. This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License 1 Contents I Trees4 1 Introduction4 2 Definitions & Terminology5 3 Tree Traversal7 3.1 Preorder Traversal................................7 3.2 Inorder Traversal.................................7 3.3 Postorder Traversal................................7 3.4 Breadth-First Search Traversal..........................8 3.5 Implementations & Data Structures.......................8 3.5.1 Preorder Implementations........................8 3.5.2 Inorder Implementation.........................9 3.5.3 Postorder Implementation........................ 10 3.5.4 BFS Implementation........................... 12 3.5.5 Tree Walk Implementations....................... 12 3.6 Operations..................................... 12 4 Binary Search Trees 14 4.1 Basic Operations................................. 15 5 Balanced Binary Search Trees 17 5.1 2-3 Trees...................................... 17 5.2 AVL Trees..................................... 17 5.3 Red-Black Trees.................................. 19 6 Optimal Binary Search Trees 19 7 Heaps 19
    [Show full text]
  • CMSC 420: Lecture 7 Randomized Search Structures: Treaps and Skip Lists
    CMSC 420 Dave Mount CMSC 420: Lecture 7 Randomized Search Structures: Treaps and Skip Lists Randomized Data Structures: A common design techlque in the field of algorithm design in- volves the notion of using randomization. A randomized algorithm employs a pseudo-random number generator to inform some of its decisions. Randomization has proved to be a re- markably useful technique, and randomized algorithms are often the fastest and simplest algorithms for a given application. This may seem perplexing at first. Shouldn't an intelligent, clever algorithm designer be able to make better decisions than a simple random number generator? The issue is that a deterministic decision-making process may be susceptible to systematic biases, which in turn can result in unbalanced data structures. Randomness creates a layer of \independence," which can alleviate these systematic biases. In this lecture, we will consider two famous randomized data structures, which were invented at nearly the same time. The first is a randomized version of a binary tree, called a treap. This data structure's name is a portmanteau (combination) of \tree" and \heap." It was developed by Raimund Seidel and Cecilia Aragon in 1989. (Remarkably, this 1-dimensional data structure is closely related to two 2-dimensional data structures, the Cartesian tree by Jean Vuillemin and the priority search tree of Edward McCreight, both discovered in 1980.) The other data structure is the skip list, which is a randomized version of a linked list where links can point to entries that are separated by a significant distance. This was invented by Bill Pugh (a professor at UMD!).
    [Show full text]
  • Red-Black Trees
    Red-Black Trees 1 Red-Black Trees balancing binary search trees relation with 2-3-4 trees 2 Insertion into a Red-Black Tree algorithm for insertion an elaborate example of an insert inserting a sequence of numbers 3 Recursive Insert Function pseudo code MCS 360 Lecture 36 Introduction to Data Structures Jan Verschelde, 20 April 2020 Introduction to Data Structures (MCS 360) Red-Black Trees L-36 20 April 2020 1 / 36 Red-Black Trees 1 Red-Black Trees balancing binary search trees relation with 2-3-4 trees 2 Insertion into a Red-Black Tree algorithm for insertion an elaborate example of an insert inserting a sequence of numbers 3 Recursive Insert Function pseudo code Introduction to Data Structures (MCS 360) Red-Black Trees L-36 20 April 2020 2 / 36 Binary Search Trees Binary search trees store ordered data. Rules to insert x at node N: if N is empty, then put x in N if x < N, insert x to the left of N if x ≥ N, insert x to the right of N Balanced tree of n elements has depth is log2(n) ) retrieval is O(log2(n)), almost constant. With rotation we make a tree balanced. Alternative to AVL tree: nodes with > 2 children. Every node in a binary tree has at most 2 children. A 2-3-4 tree has nodes with 2, 3, and 4 children. A red-black tree is a binary tree equivalent to a 2-3-4 tree. Introduction to Data Structures (MCS 360) Red-Black Trees L-36 20 April 2020 3 / 36 a red-black tree red nodes have hollow rings 11 @ 2 14 @ 1 7 @ 5 8 Four invariants: 1 A node is either red or black.
    [Show full text]
  • Balanced Binary Search Trees – AVL Trees, 2-3 Trees, B-Trees
    Balanced binary search trees – AVL trees, 2‐3 trees, B‐trees Professor Clark F. Olson (with edits by Carol Zander) AVL trees One potential problem with an ordinary binary search tree is that it can have a height that is O(n), where n is the number of items stored in the tree. This occurs when the items are inserted in (nearly) sorted order. We can fix this problem if we can enforce that the tree remains balanced while still inserting and deleting items in O(log n) time. The first (and simplest) data structure to be discovered for which this could be achieved is the AVL tree, which is names after the two Russians who discovered them, Georgy Adelson‐Velskii and Yevgeniy Landis. It takes longer (on average) to insert and delete in an AVL tree, since the tree must remain balanced, but it is faster (on average) to retrieve. An AVL tree must have the following properties: • It is a binary search tree. • For each node in the tree, the height of the left subtree and the height of the right subtree differ by at most one (the balance property). The height of each node is stored in the node to facilitate determining whether this is the case. The height of an AVL tree is logarithmic in the number of nodes. This allows insert/delete/retrieve to all be performed in O(log n) time. Here is an example of an AVL tree: 18 3 37 2 11 25 40 1 8 13 42 6 10 15 Inserting 0 or 5 or 16 or 43 would result in an unbalanced tree.
    [Show full text]
  • Binary Heaps
    Binary Heaps COL 106 Shweta Agrawal and Amit Kumar Revisiting FindMin • Application: Find the smallest ( or highest priority) item quickly – Operating system needs to schedule jobs according to priority instead of FIFO – Event simulation (bank customers arriving and departing, ordered according to when the event happened) – Find student with highest grade, employee with highest salary etc. 2 Priority Queue ADT • Priority Queue can efficiently do: – FindMin (and DeleteMin) – Insert • What if we use… – Lists: If sorted, what is the run time for Insert and FindMin? Unsorted? – Binary Search Trees: What is the run time for Insert and FindMin? – Hash Tables: What is the run time for Insert and FindMin? 3 Less flexibility More speed • Lists – If sorted: FindMin is O(1) but Insert is O(N) – If not sorted: Insert is O(1) but FindMin is O(N) • Balanced Binary Search Trees (BSTs) – Insert is O(log N) and FindMin is O(log N) • Hash Tables – Insert O(1) but no hope for FindMin • BSTs look good but… – BSTs are efficient for all Finds, not just FindMin – We only need FindMin 4 Better than a speeding BST • We can do better than Balanced Binary Search Trees? – Very limited requirements: Insert, FindMin, DeleteMin. The goals are: – FindMin is O(1) – Insert is O(log N) – DeleteMin is O(log N) 5 Binary Heaps • A binary heap is a binary tree (NOT a BST) that is: – Complete: the tree is completely filled except possibly the bottom level, which is filled from left to right – Satisfies the heap order property • every node is less than or equal to its children
    [Show full text]
  • Exercises for Algorithms and Data Structures
    Exercises for Algorithms and Data Structures Antonio Carzaniga Faculty of Informatics USI (Università della Svizzera italiana) Edition 2.10 April 2021 (with some solutions) ◮Exercise 1. Answer the following questions on the big-oh notation. Question 1: Explain what g(n) O(f (n)) means. (5’) = Question 2: Explain why it is meaningless to state that “the running time of algorithm A is at least O(n2).” (5’) Question 3: Given two functions f (log n) and g O(n), consider the following statements. = = For each statement, write whether it is true or false. For each false statement, write two functions f and g that show a counter-example.Ω (5’) g(n) O(f (n)) • = f (n) O(g(n)) • = f (n) (log (g(n))) • = f (n) (log (g(n))) • = Ω f (n) g(n) (log n) • + Θ = Question 4: For eachΩ one of the following statements, write two functions f and g that satisfy the given condition. (5’) f (n) O(g2(n)) • = f (n) ω(g(n)) • = f (n) ω(log (g(n))) • = f (n) (f (n)g(n)) • = f (n) (g(n)) (g2(n)) • = Ω + ◮Exercise 2. ΘWrite an algorithmΩ called Find-Largest that finds the largest number in an array using a divide-and-conquer strategy. Also, write the time complexity of your algorithm in terms of big-oh notation. Briefly justify your complexity analysis. (20’) ◮Exercise 3. Illustrate the execution of the merge-sort algorithm on the array A 3, 13, 89, 34, 21, 44, 99, 56, 9 =h i For each fundamental iteration or recursion of the algorithm, write the content of the array.
    [Show full text]
  • Rt0 RANGE TREES and PRIORITY SEARCH TREES Hanan Samet
    rt0 RANGE TREES AND PRIORITY SEARCH TREES Hanan Samet Computer Science Department and Center for Automation Research and Institute for Advanced Computer Studies University of Maryland College Park, Maryland 20742 e-mail: [email protected] Copyright © 1998 Hanan Samet These notes may not be reproduced by any means (mechanical or elec- tronic or any other) without the express written permission of Hanan Samet rt1 RANGE TREES • Balanced binary search tree • All data stored in the leaf nodes • Leaf nodes linked in sorted order by a doubly-linked list • Searching for [B : E] 1. find node with smallest value ≥B or largest ≤B 2. follow links until reach node with value >E • O (log2 N +F ) time to search, O (N · log2 N ) to build, and O (N ) space for N points and F answers • Ex: sort points in 2-d on their x coordinate value 55 ≤ ≥ 30 83 15 43 70 88 5 25355060808590 Denver Omaha Chicago Mobile Toronto Buffalo Atlanta Miami (5,45) (25,35) (35,40) (50,10) (60,75) (80,65) (85,15) (90,5) Copyright © 1998 by Hanan Samet rt2 2-D RANGE TREES • Binary tree of binary trees • Sort all points along one dimension (say x) and store them in the leaf nodes of a balanced binary tree such as a range tree (single line) • Each nonleaf node contains a 1-d range tree of the points in its subtrees sorted along y (double lines) • Ex: 55 A AA38 A' 13 55 8 25 43 70 30 B 83 C 5 10 15 35 40 45 65 75 38 40 B' C' (5,45) (90,5) (60,75) (25,35) (50,10) (35,40) (80,65) 23 43 (85,15) 10 70 10 35 40 45 5 15 65 75 15 D 43 E 70 F 88 G (90,5) (5,45) (60,75) (35,40) (85,15) (80,65) (50,10) (25,35) 40 D' 25 E' 70 F' 10 G' 5 HI25 35 JK50 60 LM80 85 NO90 (5,45) (25,35) (35,40) (50,10) (60,75) (80,65) (85,15) (90,5) 35 45 10 40 65 75 5 15 (25,35) (5,45) (50,10)(35,40) (80,65)(60,75) (90,5) (85,15) • Actually, don’t need the 1-d range tree in y at the root and at the sons of the root Copyright © 1998 by Hanan Samet 5 4 3 21 rt3 v g z rb SEARCHING 2-D RANGE TREES ([BX:EX],[BY:EY]) 1.
    [Show full text]
  • B-Trees and 2-3-4 Trees Reading
    B-Trees and 2-3-4 Trees Reading: • B-Trees 18 CLRS • Multi-Way Search Trees 3.3.1 and (2,4) Trees 3.3.2 GT B-trees are an extension of binary search trees: • They store more than one key at a node to divide the range of its subtree's keys into more than two subranges. 2, 7 • Every internal node has between t and 2t children. Every internal node has one more child than key. • 1, 0 3, 6 8, 9, 11 • All of the leaves must be at same level. − We will see shortly that the last two properties keep the tree balanced. Most binary search tree algorithms can easily be converted to B-trees. The amount of work done at each node increases with t (e.g. determining which branch to follow when searching for a key), but the height of the tree decreases with t, so less nodes are visited. Databases use high values of t to minimize I/O overhead: Reading each tree node requires a slow random disk access, so high branching factors reduce the number of such accesses. We will assume a low branching factor of t = 2 because our focus is on balanced data structures. But the ideas we present apply to higher branching factors. Such B-trees are often called 2-3-4 trees because their branching factor is always 2, 3, or 4. To guarantee a branching factor of 2 to 4, each internal node must store 1 to 3 keys. As with binary trees, we assume that the data associated with the key is stored with the key in the node.
    [Show full text]
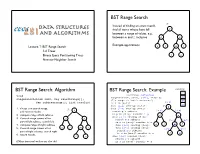
  • K-D Trees! Binary Space Partitioning Trees! L! N! Nearest-Neighbor Search!
    BST Range Search! T: Instead of finding an exact match, find all items whose keys fall k! between a range of values, e.g., between m and z, inclusive! d! p! ! Example applications:! Lecture 7: BST Range Search! a! f! m! z! k-d Trees! Binary Space Partitioning Trees! l! n! Nearest-Neighbor Search! BST Range Search: Algorithm! BST Range Search: Example! results:! z! void! searchrange, subtreerange! rangesearch(T, [m-z], [a-z], results)! n! rangesearch(Link root, Key searchrange[], (T’s range is “whole universe”)! m! Key subtreerange[], List results)! is k in [m-z]?! [a-z] ! p! does [a-j] overlap [m-z]?! T: k! 1. if root is in search range," does [l-z] overlap [m-z]?! T: [a-j] [l-z] add root to results! k! search p’s subtree! 2. compute range of left subtree! is p in [m-z]? results p! d! p! does [l-o] overlap [m-z]?! 3. if search range covers all or" d! p! search m’s subtree! [l-o] [q-z] part of left subtree, search left! is m in [m-z]? results m! 4. compute range of right subtree! does [l-l] overlap [m-z]?! a! f! m! z! 5. if search range covers all or" a! f! m! z! does [n-o] overlap [m-z]?! [l-l] [n-o] part of right subtree, search right! search n’s subtree! is n in [m-z]? results n! l! n! 6. return results! l! n! does [q-z] overlap [m-z]?! ! search z’s subtree! (Other traversal orders are also ok)! is z in [m-z]? results z! BST Range Search: Support Functions! BST Range Search: Other Details ! 1.
    [Show full text]