DOCSLIB.ORG

MAT 4810: Calculus for Elementary and Middle School Teachers MAT 4810: Calculus

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
MAT 4810: Calculus for Elementary and Middle School Teachers MAT 4810: Calculus MAT 4810: Calculus for Elementary and Middle School Teachers MAT 4810: Calculus Computing for Elementary and Middle School Teachers Derivatives & Integrals Part I Charles Delman Computing Derivatives & Integrals The Definition Part I & Meaning of the Derivative Function Local Charles Delman Coordinates Computing Derivatives of More Complicated October 17, 2016 Functions Believe You Can Solve Problems Without Being Told How! MAT 4810: Calculus for Elementary and Middle School Teachers I would like to share the following words from the introduction to Don Cohen's book. I hope you will take the attitude they Computing Derivatives & express to heart and share it with your own students. Integrals Part I Charles \You can do it! You must tell yourself that. Don't think Delman because you haven't done a problem before, that you can't do The Definition & Meaning of it, or that someone else must show you how to do it first (a the Derivative Function myth some people want to use to keep others in ignorance). Local You can do it! Don't be afraid. You've learned how to do the Coordinates hardest things you'll ever do, walking and talking { mostly by Computing Derivatives of yourself. This stuff is much easier!" More Complicated Functions Recall: Linear Rates of Change MAT 4810: Calculus for Elementary and Middle School Teachers mi To travel at 60 miles per hour ( h ) is to travel a distance Computing Derivatives & of 60∆t miles in ∆t hours: ∆d = 60∆t, where d is Integrals Part I distance in miles and t is time in hours; ∆d and ∆t are Charles the changes in these quantities, respectively. Delman A rate such as miles per hour − that is, a ratio of the The Definition & Meaning of change in output over the change in input of a function − the Derivative Function gives a purely linear relationship between these changes. Local That is, the change in output is simply a multiple of the Coordinates change in input. Computing Derivatives of More Complicated Functions Recall: Non-Linear Rates of Change MAT 4810: Calculus for Elementary and Middle For most functions, the relationship between a change in School Teachers input and the resulting change in output is not linear. Computing Derivatives & This is because the ratio between these changes is not Integrals Part I constant: the change in output is not a constant multiple Charles of the change in input. Delman When you go on a road trip, you don't drive at the same The Definition & Meaning of velocity all the time. Your average velocity over different the Derivative Function intervals of time will vary. Local Only those functions whose graphs are straight lines Coordinates exhibit a constant linear relationship between any change Computing Derivatives of in input and the resulting change in output. The graphs of More Complicated most functions are are curved. Functions The Equation of a Line MAT 4810: Calculus for Elementary and Middle (x,y) School Teachers Δy = y - y0 Computing Derivatives & (x0,y0) Δx = x - x0 Integrals Origin for Δx and Δy: Part I (Δx, Δx) = (0,0) Charles Delman The Definition & Meaning of the Derivative Given a fixed real number m, some initial input value x0, Function and corresponding output value y0 = f (x0): Local Coordinates ∆y y − y Computing 0 Derivatives of = m , = m , y − y0 = m(x − x0): More ∆x x − x0 Complicated Functions Constant rate of change is the defining property of those functions whose graphs are straight lines. Linear Functions are Central − But Not Enough MAT 4810: Calculus for Elementary and Middle School Linear functions are relatively simple to understand and Teachers have many useful properties. Computing Derivatives & There is a whole field of mathematics called linear algebra. Integrals Part I But, as even the example of a road trip illustrates, linear Charles Delman functions alone are not adequate for modeling reality or fully developing the capacity of mathematics and science. The Definition & Meaning of the Derivative To take advantage of the properties of linear functions, we Function study more complicated functions using linear functions. Local Coordinates We do this by studying the linear relationship between Computing changes in input and output at each point where such a Derivatives of More relationship applies. Complicated Functions Recall: The Definition of the Derivative Function MAT 4810: Calculus Let y = f (x) define a function f . for Elementary and Middle 0 School The definition of the derivative function, f , is Teachers Computing 0 ∆y f (x + ∆x) − f (x) Derivatives & f (x) = lim = lim Integrals ∆x!0 ∆x ∆x!0 ∆x Part I if this limit exists. Charles Delman ∆y ∆x will not necessarily approach a limit as ∆x ! 0. If The Definition f (x+∆x)−f (x) & Meaning of lim∆x!0 ∆x exists, f is differentiable at x. the Derivative 0 Function This definition is based on the idea that f (x) represents Local the instantaneous rate of change of f at input x. Coordinates 0 Computing In other words, f (x) gives the linear relationship between Derivatives of changes in input and output at point (x; y). More Complicated Functions In general, this rate will vary from point to point. Let's look at this graphically. The Slope of a Curve MAT 4810: 0 Calculus The value of the derivative f (x) gives the slope of the for Elementary and Middle curve y = f (x) at the point (x; y). School Teachers Computing Δy f(x+Δx)-f(x) Derivatives & = Integrals Δx Δx Part I Charles (x+Δx, f(x+Δx) Delman (x, f(x)) The Definition & Meaning of the Derivative Function Δx 0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 Local x x+Δx Coordinates Computing Derivatives of 0 More If f (x) is defined, the curve is \smooth" at (x; f (x)). Complicated Functions Under increasing magnification, it would look straighter and straighter. Examples & a Pattern MAT 4810: Calculus for Elementary and Middle Using this definition, we were able to calculate the School derivatives of the following functions: Teachers 0 Computing If f (x) = c, where c is a constant number, then f (x) = 0. Derivatives & Integrals The derivative of the identity function i, defined by Part I i(x) = x, is given by i 0(x) = 1. Charles If f (x) = x 2, then f 0(x) = 2x. Delman If f (x) = x 3, then f 0(x) = 3x 2. −1 0 −2 The Definition If f (x) = x , then f (x) = −x . & Meaning of the Derivative Function A clear pattern emerges, leading us to the following Local conjecture: Coordinates n 0 n−1 Computing If f (x) = x , where n is an integer, then f (x) = nx . Derivatives of More We will verify this conjecture shortly, but first let's look Complicated Functions graphically at these functions and their derivatives. Local Coordinates: The (∆x; ∆y)-Coordinate System MAT 4810: Calculus for Elementary Since the slope of the curve y = f (x) generally varies from and Middle School point to point, it is helpful to view the curve in local Teachers coordinates based at each point (x; y) = (x; f (x)). Computing Derivatives & By local coordinates, we mean that we place the origin at Integrals Part I (x; y) = (x; f (x)). Charles We have already considered the (∆x; ∆y)-coordinate Delman system, in which we graph ∆y = f (x + ∆x) − f (x). (Note The Definition & Meaning of that x is fixed in this equation.) the Derivative Function Thus, ∆x denotes change in input away from the value x Local and ∆y denotes the corresponding change in the output Coordinates of f away from the value y = f (x). Computing Derivatives of More The graph ∆y = f (x + ∆x) − f (x) is just a translation of Complicated Functions the graph of f taking a fixed value (x; y) = (x; f (x)) to the origin. The Graph ∆y = f (x + ∆x) − f (x) MAT 4810: Calculus for Elementary and Middle School Teachers Computing Δy Derivatives & Integrals Part I Charles Delman Δy = f(x+Δx) - f(x) The Definition & Meaning of the Derivative (x,y) = (x, f(x)) Function Δx Local Coordinates Computing Derivatives of More Complicated Functions Local Differential Coordinates: The (dx; dy)-Coordinate System MAT 4810: Calculus for Elementary and Middle School Teachers When we want to look at the slope of the curve y = f (x) Computing at a particular point (x; y) = (x; f (x)), it is helpful to Derivatives & Integrals graph the tangent line to the curve at (x; y). Part I The tangent line is simply the straight line passing Charles 0 Delman through (x; y) with slope f (x). The Definition Thus, the slope of the tangent line matches the slope of & Meaning of the Derivative the curve at (x; y). Function Local We use local coordinates (dx; dy) to graph the tangent Coordinates line function, which is defined by dy = f 0(x)dx. (Note Computing 0 Derivatives of that x, and hence f (x), is fixed in this equation.) More Complicated Functions 0 The Graph dy = mx · dx = f (x)dx MAT 4810: Calculus for Elementary and Middle School dy Teachers dy = mx⋅dx = f'(x)dx Computing Derivatives & Integrals Part I Charles Delman (x,y) = (x, f(x)) dx The Definition & Meaning of the Derivative Function Local Coordinates Thus, dx denotes a change in input away from the value x Computing and dy denotes the corresponding linear change in output Derivatives of More that applies at that point. Complicated Functions dy is called the differential change in f resulting from a differential change in input dx from x.
Load more

Recommended publications
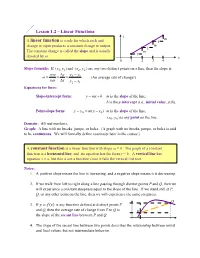
  • Lesson 1.2 – Linear Functions Y M a Linear Function Is a Rule for Which Each Unit 1 Change in Input Produces a Constant Change in Output
    Lesson 1.2 – Linear Functions y m A linear function is a rule for which each unit 1 change in input produces a constant change in output. m 1 The constant change is called the slope and is usually m 1 denoted by m. x 0 1 2 3 4 Slope formula: If (x1, y1)and (x2 , y2 ) are any two distinct points on a line, then the slope is rise y y y m 2 1 . (An average rate of change!) run x x x 2 1 Equations for lines: Slope-intercept form: y mx b m is the slope of the line; b is the y-intercept (i.e., initial value, y(0)). Point-slope form: y y0 m(x x0 ) m is the slope of the line; (x0, y0 ) is any point on the line. Domain: All real numbers. Graph: A line with no breaks, jumps, or holes. (A graph with no breaks, jumps, or holes is said to be continuous. We will formally define continuity later in the course.) A constant function is a linear function with slope m = 0. The graph of a constant function is a horizontal line, and its equation has the form y = b. A vertical line has equation x = a, but this is not a function since it fails the vertical line test. Notes: 1. A positive slope means the line is increasing, and a negative slope means it is decreasing. 2. If we walk from left to right along a line passing through distinct points P and Q, then we will experience a constant steepness equal to the slope of the line.
    [Show full text]
  • 9 Power and Polynomial Functions
    Arkansas Tech University MATH 2243: Business Calculus Dr. Marcel B. Finan 9 Power and Polynomial Functions A function f(x) is a power function of x if there is a constant k such that f(x) = kxn If n > 0, then we say that f(x) is proportional to the nth power of x: If n < 0 then f(x) is said to be inversely proportional to the nth power of x. We call k the constant of proportionality. Example 9.1 (a) The strength, S, of a beam is proportional to the square of its thickness, h: Write a formula for S in terms of h: (b) The gravitational force, F; between two bodies is inversely proportional to the square of the distance d between them. Write a formula for F in terms of d: Solution. 2 k (a) S = kh ; where k > 0: (b) F = d2 ; k > 0: A power function f(x) = kxn , with n a positive integer, is called a mono- mial function. A polynomial function is a sum of several monomial func- tions. Typically, a polynomial function is a function of the form n n−1 f(x) = anx + an−1x + ··· + a1x + a0; an 6= 0 where an; an−1; ··· ; a1; a0 are all real numbers, called the coefficients of f(x): The number n is a non-negative integer. It is called the degree of the polynomial. A polynomial of degree zero is just a constant function. A polynomial of degree one is a linear function, of degree two a quadratic function, etc. The number an is called the leading coefficient and a0 is called the constant term.
    [Show full text]
  • Polynomials.Pdf
    POLYNOMIALS James T. Smith San Francisco State University For any real coefficients a0,a1,...,an with n $ 0 and an =' 0, the function p defined by setting n p(x) = a0 + a1 x + AAA + an x for all real x is called a real polynomial of degree n. Often, we write n = degree p and call an its leading coefficient. The constant function with value zero is regarded as a real polynomial of degree –1. For each n the set of all polynomials with degree # n is closed under addition, subtraction, and multiplication by scalars. The algebra of polynomials of degree # 0 —the constant functions—is the same as that of real num- bers, and you need not distinguish between those concepts. Polynomials of degrees 1 and 2 are called linear and quadratic. Polynomial multiplication Suppose f and g are nonzero polynomials of degrees m and n: m f (x) = a0 + a1 x + AAA + am x & am =' 0, n g(x) = b0 + b1 x + AAA + bn x & bn =' 0. Their product fg is a nonzero polynomial of degree m + n: m+n f (x) g(x) = a 0 b 0 + AAA + a m bn x & a m bn =' 0. From this you can deduce the cancellation law: if f, g, and h are polynomials, f =' 0, and fg = f h, then g = h. For then you have 0 = fg – f h = f ( g – h), hence g – h = 0. Note the analogy between this wording of the cancellation law and the corresponding fact about multiplication of numbers. One of the most useful results about integer multiplication is the unique factoriza- tion theorem: for every integer f > 1 there exist primes p1 ,..., pm and integers e1 em e1 ,...,em > 0 such that f = pp1 " m ; the set consisting of all pairs <pk , ek > is unique.
    [Show full text]
  • Real Zeros of Polynomial Functions
    333353_0200.qxp 1/11/07 2:00 PM Page 91 Polynomial and Chapter 2 Rational Functions y y y 2.1 Quadratic Functions 2 2 2 2.2 Polynomial Functions of Higher Degree x x x −44−2 −44−2 −44−2 2.3 Real Zeros of Polynomial Functions 2.4 Complex Numbers 2.5 The Fundamental Theorem of Algebra Polynomial and rational functions are two of the most common types of functions 2.6 Rational Functions and used in algebra and calculus. In Chapter 2, you will learn how to graph these types Asymptotes of functions and how to find the zeros of these functions. 2.7 Graphs of Rational Functions 2.8 Quadratic Models David Madison/Getty Images Selected Applications Polynomial and rational functions have many real-life applications. The applications listed below represent a small sample of the applications in this chapter. ■ Automobile Aerodynamics, Exercise 58, page 101 ■ Revenue, Exercise 93, page 114 ■ U.S. Population, Exercise 91, page 129 ■ Impedance, Exercises 79 and 80, page 138 ■ Profit, Exercise 64, page 145 ■ Data Analysis, Exercises 41 and 42, page 154 ■ Wildlife, Exercise 43, page 155 ■ Comparing Models, Exercise 85, page 164 ■ Media, Aerodynamics is crucial in creating racecars.Two types of racecars designed and built Exercise 18, page 170 by NASCAR teams are short track cars, as shown in the photo, and super-speedway (long track) cars. Both types of racecars are designed either to allow for as much downforce as possible or to reduce the amount of drag on the racecar. 91 333353_0201.qxp 1/11/07 2:02 PM Page 92 92 Chapter 2 Polynomial and Rational Functions 2.1 Quadratic Functions The Graph of a Quadratic Function What you should learn ᭿ Analyze graphs of quadratic functions.
    [Show full text]
  • Chapter 1 Linear Functions
    Chapter 1 Linear Functions 11 Sec. 1.1: Slopes and Equations of Lines Date Lines play a very important role in Calculus where we will be approximating complicated functions with lines. We need to be experts with lines to do well in Calculus. In this section, we review slope and equations of lines. Slope of a Line: The slope of a line is defined as the vertical change (the \rise") over the horizontal change (the \run") as one travels along the line. In symbols, taking two different points (x1; y1) and (x2; y2) on the line, the slope is Change in y ∆y y − y m = = = 2 1 : Change in x ∆x x2 − x1 Example: World milk production rose at an approximately constant rate between 1996 and 2003 as shown in the following graph: where M is in million tons and t is the years since 1996. Estimate the slope and interpret it in terms of milk production. 12 Clicker Question 1: Find the slope of the line through the following pair of points (−2; 11) and (3; −4): The slope is (A) Less than -2 (B) Between -2 and 0 (C) Between 0 and 2 (D) More than 2 (E) Undefined It will be helpful to recall the following facts about intercepts. Intercepts: x-intercepts The points where a graph touches the x-axis. If we have an equation, we can find them by setting y = 0. y-intercepts The points where a graph touches the y-axis. If we have an equation, we can find them by setting x = 0.
    [Show full text]
  • Second-Order Differential Equations
    MST224 Mathematical methods Second-order differential equations This publication forms part of an Open University module. Details of this and other Open University modules can be obtained from the Student Registration and Enquiry Service, The Open University, PO Box 197, Milton Keynes MK7 6BJ, United Kingdom (tel. +44 (0)845 300 6090; email [email protected]). Alternatively, you may visit the Open University website at www.open.ac.uk where you can learn more about the wide range of modules and packs offered at all levels by The Open University. To purchase a selection of Open University materials visit www.ouw.co.uk, or contact Open University Worldwide, Walton Hall, Milton Keynes MK7 6AA, United Kingdom for a brochure (tel. +44 (0)1908 858779; fax +44 (0)1908 858787; email [email protected]). Note to reader Mathematical/statistical content at the Open University is usually provided to students in printed books, with PDFs of the same online. This format ensures that mathematical notation is presented accurately and clearly. The PDF of this extract thus shows the content exactly as it would be seen by an Open University student. Please note that the PDF may contain references to other parts of the module and/or to software or audio-visual components of the module. Regrettably mathematical and statistical content in PDF files is unlikely to be accessible using a screenreader, and some OpenLearn units may have PDF files that are not searchable. You may need additional help to read these documents. The Open University, Walton Hall, Milton Keynes, MK7 6AA.
    [Show full text]
  • Linear and Quadratic Functions
    Chapter 2 Linear and Quadratic Functions 2.1 Linear Functions We now begin the study of families of functions. Our first family, linear functions, are old friends as we shall soon see. Recall from Geometry that two distinct points in the plane determine a unique line containing those points, as indicated below. P (x0; y0) Q (x1; y1) To give a sense of the `steepness' of the line, we recall that we can compute the slope of the line using the formula below. Equation 2.1. The slope m of the line containing the points P (x0; y0) and Q (x1; y1) is: y − y m = 1 0 ; x1 − x0 provided x1 =6 x0. A couple of notes about Equation 2.1 are in order. First, don't ask why we use the letter `m' to represent slope. There are many explanations out there, but apparently no one really knows for 1 sure. Secondly, the stipulation x1 =6 x0 ensures that we aren't trying to divide by zero. The reader is invited to pause to think about what is happening geometrically; the anxious reader can skip along to the next example. Example 2.1.1. Find the slope of the line containing the following pairs of points, if it exists. Plot each pair of points and the line containing them. 1See www.mathforum.org or www.mathworld.wolfram.com for discussions on this topic. 152 Linear and Quadratic Functions 1. P (0; 0), Q(2; 4) 2. P (−1; 2), Q(3; 4) 3. P (−2; 3), Q(2; −3) 4.
    [Show full text]
  • Math 431 - Real Analysis I Homework Due October 31
    Math 431 - Real Analysis I Homework due October 31 In class, we learned that a function f : S ! T between metric spaces (S; dS) and (T; dT ) is continuous if and only if the pre-image of every open set in T is open in S. In other words, f is continuous if for all open U ⊂ T , the pre-image f −1(U) ⊂ S is open in S. Question 1. Let S; T , and R be metric spaces and let f : S ! T and g : T ! R. We can define the composition function g ◦ f : S ! R by g ◦ f(s) = g(f(s)): (a) Let U ⊂ R. Show that (g ◦ f)−1(U) = f −1 g−1 (U) (b) Use (a) to show that if f and g are continuous, then the composition g ◦ f is also continuous Solution 1. (a) We will show that (g ◦ f)−1(U) = f −1 g−1 (U) by showing that (g ◦ f)−1(U) ⊂ f −1 g−1 (U) and f −1 g−1 (U) ⊂ (g ◦ f)−1(U). For the first direction, let x 2 (g ◦ f)−1(U). Then, g ◦ f(x) 2 U. Thus, g(f(x)) 2 U. Since g(f(x)) 2 U, then f(x) 2 g−1(U). Continuing we get that x 2 f −1(g−1(U). Thus, (g ◦ f)−1(U) ⊂ f −1 g−1 (U) : Conversely, assume that x 2 f −1 g−1 (U). Then, f(x) 2 g−1(U). Furthermore, g(f(x)) 2 U. Thus, g ◦ f(x) 2 U.
    [Show full text]
  • 6.042J Lecture 19: Solutions
    Massachusetts Institute of Technology 6.042J/18.062J, Spring ’10: Mathematics for Computer Science March 17 Prof. Albert R. Meyer revised March 15, 2010, 675 minutes Solutions to In-Class Problems Week 7, Wed. Problem 1. The Elementary 18.01 Functions (F18’s) are the set of functions of one real variable defined recur­ sively as follows: Base cases: • The identity function, id(x) ::= x is an F18, • any constant function is an F18, • the sine function is an F18, Constructor cases: If f; g are F18’s, then so are 1. f + g, fg, eg (the constant e), 2. the inverse function f (−1), 3. the composition f ◦ g. (a) Prove that the function 1=x is an F18. Warning: Don’t confuse 1=x = x−1 with the inverse, id(−1) of the identity function id(x). The inverse id(−1) is equal to id. Solution. log x is the inverse of ex so log x 2 F18. Therefore so is c · log x for any constant c, and c log x c −1 hence e = x 2 F18. Now let c = −1 to get x = 1=x 2 F18.1 � (b) Prove by Structural Induction on this definition that the Elementary 18.01 Functions are closed under taking derivatives. That is, show that if f(x) is an F18, then so is f 0 ::= df=dx. (Just work out 2 or 3 of the most interesting constructor cases; you may skip the less interesting ones.) Solution. Proof. By Structural Induction on def of f 2 F18. The induction hypothesis is the above statement to be shown.
    [Show full text]
  • Quasi-Random Multilinear Polynomials 3
    QUASI-RANDOM MULTILINEAR POLYNOMIALS GIL KALAI AND LEONARD J. SCHULMAN ABSTRACT. We consider multilinear Littlewood polynomials, polynomials in n variables in which a specified set of monomials U have 1 coefficients, and all other coefficients are 0. We provide upper ± and lower bounds (which are close for U of degree below log n) on the minimum, over polynomials h consistent with U, of the maximum of h over 1 assignments to the variables. (This is a variant of a question posed by Erd¨os regarding the| maximum| ± on the unit disk of univariate polynomials of given degree with unit coefficients.) We outline connections to the theory of quasi-random graphs and hyper- graphs, and to statistical mechanics models. Our methods rely on the analysis of the Gale-Berlekamp game; on the constructive side of the generic chaining method; on a Khintchine-type inequality for polynomials of degree greater than 1; and on Bernstein’s approximation theory inequality. 1. INTRODUCTION In this article a Littlewood polynomial h is a polynomial in n variables in which all nonzero monomial S coefficients are units. Such h has the expansion h(x1,...,xn)= S hSx , where S is a nonempty S subset of [n], x = xi, and hS C, where C is the unit circleP in C. If all nonzero hS are in i S ∈ 1 we say the polynomialQ ∈ is real. Given a set U of monomials in n variables, always excluding the ± empty monomial (constant function), the real (or complex) Littlewood family of polynomials R (or LU, U,C) is the set of real (or complex) Littlewood polynomials whose set of nonzero coefficients equals UL.
    [Show full text]
  • 18.03 Differential Equations
    18.03 LECTURE NOTES, SPRING 2018 BJORN POONEN These are an approximation of what was covered in lecture. (Please clear your browser's cache before reloading this file to make sure you are getting the current version.) This PDF file is divided into sections; the instructions for viewing the table of contents depend on which PDF viewer you are using. If your PDF viewer is linked to a browser, you should be able to click on URLs, such as the one below to go to the online mathlets: http://mathlets.org/mathlets/ Small text contains a technical explanation that you might want to ignore when reading for the first time. February 7 1. Solutions to differential equations 1.1. Introduction. A differential equation (DE) is an equation relating an unknown function and some of its derivatives. DEs arise in engineering, chemistry, biology, physics, economics, etc., because many laws of nature describe the instantaneous rate of change of a quantity in terms of current conditions. Overall goals: to learn how to • model real-world problems with DEs. • solve DEs exactly when possible, or else solve numerically (get an approximate solution) • extract qualitative information from a DE, whether or not it can be solved. (There is ongoing research on these questions. For instance, there is a $1,000,000 prize for understanding the solutions to the Navier{Stokes equations modeling fluid flow.) 1.2. Notation and units. (To be done in recitation on Feb. 6.) Notation for higher derivatives of a function y(t): 1 dy first derivative:y _, y0, dt d2y second derivative:y ¨, y00, dt2 ..
    [Show full text]
  • Chapter 1: List of Topics 1.1­ Functions
    Helen Troupis Ralph Raskas Micaila Edlin Chapter 1: List of Topics 1.1­ Functions Topics: * Describe subsets of real numbers. * Identify and evaluate functions and state their domains. Terms: * Set­Builder Notation: An expression that describes a set of numbers by using the properties of numbers in the set to define the set. EX. {x|x ≥ 8,x ε ω } *Interval Notation: An expression the uses inequalities to describe subsets of real numbers. * Function: A relation that assigns to each element in the domain one element in the range. * Function Notation: An equation of y in terms of x can be rewritten *Independent Variable: The variable in a function that represents any value in the domain. *Dependent Variable: The variable in a function the represents any value in the range. *Implied Domain: In a function with an unspecified domain, the set of all real numbers for which the expression used to define the function is real. *Piecewise­defined function: A function that is defined using two or more expressions for different intervals of the domain. Key Concepts: * Q=rationals * I=irrationals * Z=integers * W=wholes * N=naturals 1.2 ­ Analyzing Graphs of Equations and Relations Topics: * Use graphs of functions to estimate function values and find domains, ranges, y­intercepts, and zeros of functions. * Explore symmetries of graphs, and identify even and odd functions. Terms: * Zeros: The x­intercepts of the graph of a function. * Roots: For a function f(x), a solution of the equation f(x)=0. * Line symmetry: Describes graphs that can be folded along a line so the two halves match.
    [Show full text]