DOCSLIB.ORG

Constant & Linear Polynomials

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Constant & Linear Polynomials Constant & Linear Polynomials Constant polynomials A constant polynomial is the same thing as a constant function. That is, a constant polynomial is a function of the form p(x)=c 5 for some number c. For example, p(x)= 3 or q(x)= 7. The output of a constant polynomial does− not depend− on the input (notice that there is no x on the right side of the equation p(x)=c). Constant polynomials are also called degree 0 polynomials. The graph of a constant polynomial is a horizontal line. A constant poly- nomial does not have any roots unless it is the polynomial p(x)=0. ************* Linear polynomials A linear polynomial is any polynomial defined by an equation of the form p(x)=ax + b where a and b are real numbers and a =0.Forexample,p(x)=3x 7and 13 5 6 − q(x)=−4 x+ 3 are linear polynomials. A linear polynomial is the same thing as a degree 1 polynomial. Roots of linear polynomials Every linear polynomial has exactly one root. Finding the root is just a matter of basic algebra. Problem: Find the root of p(x)=3x 7. − Solution: The root of p(x)isthenumber↵ such that p(↵)=0.Inthis 7 7 problem that means that 3↵ 7 = 0. Hence 3↵ =7,so↵ = 3. Thus, 3 is the root of 3x 7. − − ************* 141 SlopeSlope TheThe slope slope of a of line a line is the is theratio ratio of the of thechange change in the in thesecond second coordinate coordinate to the to the changechange in the in the first first coordinate. coordinate. In di In↵erent different words, words, if a if line a line contains contains the the two two pointspoints (x1,y (x11)and(,y1)and(x2,yx22),,y then2), then the the slope slope is the is the change change in the in they-coordinatey-coordinate –whichequals–whichequalsy2 yy1 –y divided– divided by the by the change change in the in thex-coordinatex-coordinate – which – which − 2 − 1 equalsequalsx2 xx1. x . − 2 − 1 SlopeSlope of line of line containing containing (x1,y (x11)and(,y1)and(x2,yx22):,y2): y2 yy1 y − 2 − 1 x2 xx1 x − 2 − 1 Example:Example:TheThe slope slope of the of the line line containing containing the the two two points points ( 1 (, 4)1, and4) and (2, 5) (2, 5) − equalsequals − 5 54 4 1 1 − − = = 2 2( 1)( 1)3 3 − −− − ************************** 142 2 GraphingGraphing linear linear polynomials polynomials LetLetp(px()=x)=axaxwherewherea aisis a a number number that that does does not not equal equal 0. 0. This This polynomial polynomial isis an an example example of of a a linear linear polynomial. polynomial. The graph of p(x)=ax is a straight line that passes through (0, 0) R2 2 The graph of p(x)=ax is a straight line that passes through (0, 0) ⇥R andand has has slope slope equal equal to toa.a. We We can can check check this this by by graphing graphing it. it. The The point2 point (0(0,a,a0)0) = = (0 (0, 0), 0) is is in in the the graph, graph, as as are are the the points points (1 (1,a,a),), (2 (2, 2,a2),a), (3 (3, 3,a3),...a),... and and ( (1,1, a),a), ( (2,2, 2a2),a), ( (3,3, 3a3),...a),... −− −− −− −− −− −− BecauseBecause the the graph graph of ofaxax++b bisis the the graph graph of ofaxaxshiftedshifted up up or or down down by byb b –dependingonwhether–dependingonwhetherb bisis positive positive or or negative negative – – the the graph graph of ofaxax++b bisis a a 2 straightstraight line line that that passes passes through through (0 (0,b,b) ) RR2 andand has has slope slope equal equal to toa.a. 2⇥ Problem:Problem:GraphGraphp(px()=x)=2x2x+4.+4. −− Solution:Solution:TheThe graph graph of of 2x2+4x+4 is is the the graph graph of of 2x2x“shifted“shifted up” up” by by 4. 4. Draw Draw 2x, which is the line− of− slope 2thatpassesthrough(0−− , 0), and then shift −2x, which is the line of slope −2thatpassesthrough(0, 0), and then shift it−it up up to to the the line line that that passes passes through through− (0 (0, 4), 4) and and is is parallel parallel to to 2x2.x. 1433 −− . AnotherAnother solution: solution:ToTo graph graph a a linear linear polynomial, polynomial, find find two two points points in in the the Anothergraph,graph, and and solution: then then draw drawTo the the graph straight straight a linear line line that that polynomial, passes passes through through find two them. them. points in the graph,SinceSince andp(px(x)= then)= draw2x2x+4has2asaroot,ithasan+4has2asaroot,ithasan the straight line that passes throughxx-intercept-intercept them. at at 2. 2. The They-y- interceptSince p(x is)= the− point−2x +4has2asaroot,ithasan in the graph whose first coordinatex-intercept equals at 0, 2. and The that’sy- intercept is the point− in the graph whose first coordinate equals 0, and that’s interceptthe point is (0 the,p(0)) point = in (0 the, 4). graph To graph whose2 firstx +4,drawthelinepassingthrough coordinate equals 0, and that’s the point (0,p(0)) = (0, 4). To graph −2x +4,drawthelinepassingthrough thethethe pointxx-and-and (0y,p-intercepts.y-intercepts.(0)) = (0, 4). To graph −2x +4,drawthelinepassingthrough the x-andy-intercepts. − BehindBehind the the name. name. DegreeDegree 1 1 polynomials polynomials are are called called linear linear polynomials polynomials Behindbecausebecause their the their graphs name. graphs are areDegree straight straight 1 polynomialslines. lines. are called linear polynomials because their graphs are straight lines. ************************** ************* 1444 4 Exercises For #1-3, match the numbered constant polynomials with their lettered graphs. 1.) p(x)=3 2.) q(x)= 23.)f(x)=⇡ − A.) B.) C.) /L5/L5/L5 S SS ------ 3 33 --- Find the root for each of the linear polynomials given in #4-9. 4.) p(x)=2x 35.)q(x)=x +2 6.) r(x)= 4x + 6 − −3 7 7.) f(x)=4x 68.)g(x)=2x 8 9.) h(x)=x 3 − 9 − 5 − For #10-13, find the slope of the line that passes through the two points that are given. 10.) (2, 3) and (3, 5) 11.) (4, 5) and ( 2, 7) − 12.) ( 3, 4) and (10, 0) 13.) (1, 5) and (3, 2) − − 145 4/4/4/ )L,L )L,L )L,L For #14-16, match the given slope of a line with the lettered lines drawn. 14.) slope 315.)slope216.)slope0 − A.) B.) C.) For each of the linear polynomials given in #17-20, find the slope, x- intercept, and y-intercept of its graph. The slope of the graph of a linear polynomial is its leading coefficient. The x-intercept is the root of the linear polynomial. The y-intercept is its constant term. 17.) p(x)=2x +1 18.) q(x)=x 5 − 19.) f(x)= 3x +4 20.) g(x)=4x 7 − − 146 /L5 S -- 3 - /L5 S -- 3 - /L5 S -- 3 - For4/ #21-23, match the given linear polynomial with its lettered graph. 21.) p(x)=2x +6 22.) q(x)= 3x 223.)f(x)=x 4 − − − A.) B.) C.) 4/ 24.) Claudia owns a coconut collecting company. She has to pay $200 for acoconutcollectinglicensetorunhercompany,andshemakes$3forevery4/ coconut she collects. If x is the number of coconuts she collects, and p(x)is the number of dollars her company earns, then find an equation for p(x). 25.) Spencer is payed $400 to collect coconuts no matter how many co- conuts he collects. Because he is collecting coconuts for a flat fee, the local government does not require Spencer to purchase a coconut collecting license. If q(x)isthenumberofdollarsheearnsforcollectingx coconuts, what is the equation that defines q(x)? 26.) If Claudia and Spencer collect the same number of coconuts, then how many coconuts would Claudia have to collect for her company to earn at least as much money as Spencer? 147.
Load more

Recommended publications
  • Chapter 11. Three Dimensional Analytic Geometry and Vectors
    Chapter 11. Three dimensional analytic geometry and vectors. Section 11.5 Quadric surfaces. Curves in R2 : x2 y2 ellipse + =1 a2 b2 x2 y2 hyperbola − =1 a2 b2 parabola y = ax2 or x = by2 A quadric surface is the graph of a second degree equation in three variables. The most general such equation is Ax2 + By2 + Cz2 + Dxy + Exz + F yz + Gx + Hy + Iz + J =0, where A, B, C, ..., J are constants. By translation and rotation the equation can be brought into one of two standard forms Ax2 + By2 + Cz2 + J =0 or Ax2 + By2 + Iz =0 In order to sketch the graph of a quadric surface, it is useful to determine the curves of intersection of the surface with planes parallel to the coordinate planes. These curves are called traces of the surface. Ellipsoids The quadric surface with equation x2 y2 z2 + + =1 a2 b2 c2 is called an ellipsoid because all of its traces are ellipses. 2 1 x y 3 2 1 z ±1 ±2 ±3 ±1 ±2 The six intercepts of the ellipsoid are (±a, 0, 0), (0, ±b, 0), and (0, 0, ±c) and the ellipsoid lies in the box |x| ≤ a, |y| ≤ b, |z| ≤ c Since the ellipsoid involves only even powers of x, y, and z, the ellipsoid is symmetric with respect to each coordinate plane. Example 1. Find the traces of the surface 4x2 +9y2 + 36z2 = 36 1 in the planes x = k, y = k, and z = k. Identify the surface and sketch it. Hyperboloids Hyperboloid of one sheet. The quadric surface with equations x2 y2 z2 1.
    [Show full text]
  • An Introduction to Mathematical Modelling
    An Introduction to Mathematical Modelling Glenn Marion, Bioinformatics and Statistics Scotland Given 2008 by Daniel Lawson and Glenn Marion 2008 Contents 1 Introduction 1 1.1 Whatismathematicalmodelling?. .......... 1 1.2 Whatobjectivescanmodellingachieve? . ............ 1 1.3 Classificationsofmodels . ......... 1 1.4 Stagesofmodelling............................... ....... 2 2 Building models 4 2.1 Gettingstarted .................................. ...... 4 2.2 Systemsanalysis ................................. ...... 4 2.2.1 Makingassumptions ............................. .... 4 2.2.2 Flowdiagrams .................................. 6 2.3 Choosingmathematicalequations. ........... 7 2.3.1 Equationsfromtheliterature . ........ 7 2.3.2 Analogiesfromphysics. ...... 8 2.3.3 Dataexploration ............................... .... 8 2.4 Solvingequations................................ ....... 9 2.4.1 Analytically.................................. .... 9 2.4.2 Numerically................................... 10 3 Studying models 12 3.1 Dimensionlessform............................... ....... 12 3.2 Asymptoticbehaviour ............................. ....... 12 3.3 Sensitivityanalysis . ......... 14 3.4 Modellingmodeloutput . ....... 16 4 Testing models 18 4.1 Testingtheassumptions . ........ 18 4.2 Modelstructure.................................. ...... 18 i 4.3 Predictionofpreviouslyunuseddata . ............ 18 4.3.1 Reasonsforpredictionerrors . ........ 20 4.4 Estimatingmodelparameters . ......... 20 4.5 Comparingtwomodelsforthesamesystem . .........
    [Show full text]
  • A Quick Algebra Review
    A Quick Algebra Review 1. Simplifying Expressions 2. Solving Equations 3. Problem Solving 4. Inequalities 5. Absolute Values 6. Linear Equations 7. Systems of Equations 8. Laws of Exponents 9. Quadratics 10. Rationals 11. Radicals Simplifying Expressions An expression is a mathematical “phrase.” Expressions contain numbers and variables, but not an equal sign. An equation has an “equal” sign. For example: Expression: Equation: 5 + 3 5 + 3 = 8 x + 3 x + 3 = 8 (x + 4)(x – 2) (x + 4)(x – 2) = 10 x² + 5x + 6 x² + 5x + 6 = 0 x – 8 x – 8 > 3 When we simplify an expression, we work until there are as few terms as possible. This process makes the expression easier to use, (that’s why it’s called “simplify”). The first thing we want to do when simplifying an expression is to combine like terms. For example: There are many terms to look at! Let’s start with x². There Simplify: are no other terms with x² in them, so we move on. 10x x² + 10x – 6 – 5x + 4 and 5x are like terms, so we add their coefficients = x² + 5x – 6 + 4 together. 10 + (-5) = 5, so we write 5x. -6 and 4 are also = x² + 5x – 2 like terms, so we can combine them to get -2. Isn’t the simplified expression much nicer? Now you try: x² + 5x + 3x² + x³ - 5 + 3 [You should get x³ + 4x² + 5x – 2] Order of Operations PEMDAS – Please Excuse My Dear Aunt Sally, remember that from Algebra class? It tells the order in which we can complete operations when solving an equation.
    [Show full text]
  • Example 10.8 Testing the Steady-State Approximation. ⊕ a B C C a B C P + → → + → D Dt K K K K K K [ ]
    Example 10.8 Testing the steady-state approximation. Å The steady-state approximation contains an apparent contradiction: we set the time derivative of the concentration of some species (a reaction intermediate) equal to zero — implying that it is a constant — and then derive a formula showing how it changes with time. Actually, there is no contradiction since all that is required it that the rate of change of the "steady" species be small compared to the rate of reaction (as measured by the rate of disappearance of the reactant or appearance of the product). But exactly when (in a practical sense) is this approximation appropriate? It is often applied as a matter of convenience and justified ex post facto — that is, if the resulting rate law fits the data then the approximation is considered justified. But as this example demonstrates, such reasoning is dangerous and possible erroneous. We examine the mechanism A + B ¾¾1® C C ¾¾2® A + B (10.12) 3 C® P (Note that the second reaction is the reverse of the first, so we have a reversible second-order reaction followed by an irreversible first-order reaction.) The rate constants are k1 for the forward reaction of the first step, k2 for the reverse of the first step, and k3 for the second step. This mechanism is readily solved for with the steady-state approximation to give d[A] k1k3 = - ke[A][B] with ke = (10.13) dt k2 + k3 (TEXT Eq. (10.38)). With initial concentrations of A and B equal, hence [A] = [B] for all times, this equation integrates to 1 1 = + ket (10.14) [A] A0 where A0 is the initial concentration (equal to 1 in work to follow).
    [Show full text]
  • Writing the Equation of a Line
    Name______________________________ Writing the Equation of a Line When you find the equation of a line it will be because you are trying to draw scientific information from it. In math, you write equations like y = 5x + 2 This equation is useless to us. You will never graph y vs. x. You will be graphing actual data like velocity vs. time. Your equation should therefore be written as v = (5 m/s2) t + 2 m/s. See the difference? You need to use proper variables and units in order to compare it to theory or make actual conclusions about physical principles. The second equation tells me that when the data collection began (t = 0), the velocity of the object was 2 m/s. It also tells me that the velocity was changing at 5 m/s every second (m/s/s = m/s2). Let’s practice this a little, shall we? Force vs. mass F (N) y = 6.4x + 0.3 m (kg) You’ve just done a lab to see how much force was necessary to get a mass moving along a rough surface. Excel spat out the graph above. You labeled each axis with the variable and units (well done!). You titled the graph starting with the variable on the y-axis (nice job!). Now we turn to the equation. First we replace x and y with the variables we actually graphed: F = 6.4m + 0.3 Then we add units to our slope and intercept. The slope is found by dividing the rise by the run so the units will be the units from the y-axis divided by the units from the x-axis.
    [Show full text]
  • Algorithmic Factorization of Polynomials Over Number Fields
    Rose-Hulman Institute of Technology Rose-Hulman Scholar Mathematical Sciences Technical Reports (MSTR) Mathematics 5-18-2017 Algorithmic Factorization of Polynomials over Number Fields Christian Schulz Rose-Hulman Institute of Technology Follow this and additional works at: https://scholar.rose-hulman.edu/math_mstr Part of the Number Theory Commons, and the Theory and Algorithms Commons Recommended Citation Schulz, Christian, "Algorithmic Factorization of Polynomials over Number Fields" (2017). Mathematical Sciences Technical Reports (MSTR). 163. https://scholar.rose-hulman.edu/math_mstr/163 This Dissertation is brought to you for free and open access by the Mathematics at Rose-Hulman Scholar. It has been accepted for inclusion in Mathematical Sciences Technical Reports (MSTR) by an authorized administrator of Rose-Hulman Scholar. For more information, please contact [email protected]. Algorithmic Factorization of Polynomials over Number Fields Christian Schulz May 18, 2017 Abstract The problem of exact polynomial factorization, in other words expressing a poly- nomial as a product of irreducible polynomials over some field, has applications in algebraic number theory. Although some algorithms for factorization over algebraic number fields are known, few are taught such general algorithms, as their use is mainly as part of the code of various computer algebra systems. This thesis provides a summary of one such algorithm, which the author has also fully implemented at https://github.com/Whirligig231/number-field-factorization, along with an analysis of the runtime of this algorithm. Let k be the product of the degrees of the adjoined elements used to form the algebraic number field in question, let s be the sum of the squares of these degrees, and let d be the degree of the polynomial to be factored; then the runtime of this algorithm is found to be O(d4sk2 + 2dd3).
    [Show full text]
  • January 10, 2010 CHAPTER SIX IRREDUCIBILITY and FACTORIZATION §1. BASIC DIVISIBILITY THEORY the Set of Polynomials Over a Field
    January 10, 2010 CHAPTER SIX IRREDUCIBILITY AND FACTORIZATION §1. BASIC DIVISIBILITY THEORY The set of polynomials over a field F is a ring, whose structure shares with the ring of integers many characteristics. A polynomials is irreducible iff it cannot be factored as a product of polynomials of strictly lower degree. Otherwise, the polynomial is reducible. Every linear polynomial is irreducible, and, when F = C, these are the only ones. When F = R, then the only other irreducibles are quadratics with negative discriminants. However, when F = Q, there are irreducible polynomials of arbitrary degree. As for the integers, we have a division algorithm, which in this case takes the form that, if f(x) and g(x) are two polynomials, then there is a quotient q(x) and a remainder r(x) whose degree is less than that of g(x) for which f(x) = q(x)g(x) + r(x) . The greatest common divisor of two polynomials f(x) and g(x) is a polynomial of maximum degree that divides both f(x) and g(x). It is determined up to multiplication by a constant, and every common divisor divides the greatest common divisor. These correspond to similar results for the integers and can be established in the same way. One can determine a greatest common divisor by the Euclidean algorithm, and by going through the equations in the algorithm backward arrive at the result that there are polynomials u(x) and v(x) for which gcd (f(x), g(x)) = u(x)f(x) + v(x)g(x) .
    [Show full text]
  • Differentiation Rules (Differential Calculus)
    Differentiation Rules (Differential Calculus) 1. Notation The derivative of a function f with respect to one independent variable (usually x or t) is a function that will be denoted by D f . Note that f (x) and (D f )(x) are the values of these functions at x. 2. Alternate Notations for (D f )(x) d d f (x) d f 0 (1) For functions f in one variable, x, alternate notations are: Dx f (x), dx f (x), dx , dx (x), f (x), f (x). The “(x)” part might be dropped although technically this changes the meaning: f is the name of a function, dy 0 whereas f (x) is the value of it at x. If y = f (x), then Dxy, dx , y , etc. can be used. If the variable t represents time then Dt f can be written f˙. The differential, “d f ”, and the change in f ,“D f ”, are related to the derivative but have special meanings and are never used to indicate ordinary differentiation. dy 0 Historical note: Newton used y,˙ while Leibniz used dx . About a century later Lagrange introduced y and Arbogast introduced the operator notation D. 3. Domains The domain of D f is always a subset of the domain of f . The conventional domain of f , if f (x) is given by an algebraic expression, is all values of x for which the expression is defined and results in a real number. If f has the conventional domain, then D f usually, but not always, has conventional domain. Exceptions are noted below.
    [Show full text]
  • The Geometry of the Phase Diffusion Equation
    J. Nonlinear Sci. Vol. 10: pp. 223–274 (2000) DOI: 10.1007/s003329910010 © 2000 Springer-Verlag New York Inc. The Geometry of the Phase Diffusion Equation N. M. Ercolani,1 R. Indik,1 A. C. Newell,1,2 and T. Passot3 1 Department of Mathematics, University of Arizona, Tucson, AZ 85719, USA 2 Mathematical Institute, University of Warwick, Coventry CV4 7AL, UK 3 CNRS UMR 6529, Observatoire de la Cˆote d’Azur, 06304 Nice Cedex 4, France Received on October 30, 1998; final revision received July 6, 1999 Communicated by Robert Kohn E E Summary. The Cross-Newell phase diffusion equation, (|k|)2T =∇(B(|k|) kE), kE =∇2, and its regularization describes natural patterns and defects far from onset in large aspect ratio systems with rotational symmetry. In this paper we construct explicit solutions of the unregularized equation and suggest candidates for its weak solutions. We confirm these ideas by examining a fourth-order regularized equation in the limit of infinite aspect ratio. The stationary solutions of this equation include the minimizers of a free energy, and we show these minimizers are remarkably well-approximated by a second-order “self-dual” equation. Moreover, the self-dual solutions give upper bounds for the free energy which imply the existence of weak limits for the asymptotic minimizers. In certain cases, some recent results of Jin and Kohn [28] combined with these upper bounds enable us to demonstrate that the energy of the asymptotic minimizers converges to that of the self-dual solutions in a viscosity limit. 1. Introduction The mathematical models discussed in this paper are motivated by physical systems, far from equilibrium, which spontaneously form patterns.
    [Show full text]
  • 2.4 Algebra of Polynomials ([1], P.136-142) in This Section We Will Give a Brief Introduction to the Algebraic Properties of the Polynomial Algebra C[T]
    2.4 Algebra of polynomials ([1], p.136-142) In this section we will give a brief introduction to the algebraic properties of the polynomial algebra C[t]. In particular, we will see that C[t] admits many similarities to the algebraic properties of the set of integers Z. Remark 2.4.1. Let us first recall some of the algebraic properties of the set of integers Z. - division algorithm: given two integers w, z 2 Z, with jwj ≤ jzj, there exist a, r 2 Z, with 0 ≤ r < jwj such that z = aw + r. Moreover, the `long division' process allows us to determine a, r. Here r is the `remainder'. - prime factorisation: for any z 2 Z we can write a1 a2 as z = ±p1 p2 ··· ps , where pi are prime numbers. Moreover, this expression is essentially unique - it is unique up to ordering of the primes appearing. - Euclidean algorithm: given integers w, z 2 Z there exists a, b 2 Z such that aw + bz = gcd(w, z), where gcd(w, z) is the `greatest common divisor' of w and z. In particular, if w, z share no common prime factors then we can write aw + bz = 1. The Euclidean algorithm is a process by which we can determine a, b. We will now introduce the polynomial algebra in one variable. This is simply the set of all polynomials with complex coefficients and where we make explicit the C-vector space structure and the multiplicative structure that this set naturally exhibits. Definition 2.4.2. - The C-algebra of polynomials in one variable, is the quadruple (C[t], α, σ, µ)43 where (C[t], α, σ) is the C-vector space of polynomials in t with C-coefficients defined in Example 1.2.6, and µ : C[t] × C[t] ! C[t];(f , g) 7! µ(f , g), is the `multiplication' function.
    [Show full text]
  • Numerical Algebraic Geometry and Algebraic Kinematics
    Numerical Algebraic Geometry and Algebraic Kinematics Charles W. Wampler∗ Andrew J. Sommese† January 14, 2011 Abstract In this article, the basic constructs of algebraic kinematics (links, joints, and mechanism spaces) are introduced. This provides a common schema for many kinds of problems that are of interest in kinematic studies. Once the problems are cast in this algebraic framework, they can be attacked by tools from algebraic geometry. In particular, we review the techniques of numerical algebraic geometry, which are primarily based on homotopy methods. We include a review of the main developments of recent years and outline some of the frontiers where further research is occurring. While numerical algebraic geometry applies broadly to any system of polynomial equations, algebraic kinematics provides a body of interesting examples for testing algorithms and for inspiring new avenues of work. Contents 1 Introduction 4 2 Notation 5 I Fundamentals of Algebraic Kinematics 6 3 Some Motivating Examples 6 3.1 Serial-LinkRobots ............................... ..... 6 3.1.1 Planar3Rrobot ................................. 6 3.1.2 Spatial6Rrobot ................................ 11 3.2 Four-BarLinkages ................................ 13 3.3 PlatformRobots .................................. 18 ∗General Motors Research and Development, Mail Code 480-106-359, 30500 Mound Road, Warren, MI 48090- 9055, U.S.A. Email: [email protected] URL: www.nd.edu/˜cwample1. This material is based upon work supported by the National Science Foundation under Grant DMS-0712910 and by General Motors Research and Development. †Department of Mathematics, University of Notre Dame, Notre Dame, IN 46556-4618, U.S.A. Email: [email protected] URL: www.nd.edu/˜sommese. This material is based upon work supported by the National Science Foundation under Grant DMS-0712910 and the Duncan Chair of the University of Notre Dame.
    [Show full text]
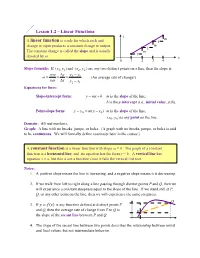
  • Lesson 1.2 – Linear Functions Y M a Linear Function Is a Rule for Which Each Unit 1 Change in Input Produces a Constant Change in Output
    Lesson 1.2 – Linear Functions y m A linear function is a rule for which each unit 1 change in input produces a constant change in output. m 1 The constant change is called the slope and is usually m 1 denoted by m. x 0 1 2 3 4 Slope formula: If (x1, y1)and (x2 , y2 ) are any two distinct points on a line, then the slope is rise y y y m 2 1 . (An average rate of change!) run x x x 2 1 Equations for lines: Slope-intercept form: y mx b m is the slope of the line; b is the y-intercept (i.e., initial value, y(0)). Point-slope form: y y0 m(x x0 ) m is the slope of the line; (x0, y0 ) is any point on the line. Domain: All real numbers. Graph: A line with no breaks, jumps, or holes. (A graph with no breaks, jumps, or holes is said to be continuous. We will formally define continuity later in the course.) A constant function is a linear function with slope m = 0. The graph of a constant function is a horizontal line, and its equation has the form y = b. A vertical line has equation x = a, but this is not a function since it fails the vertical line test. Notes: 1. A positive slope means the line is increasing, and a negative slope means it is decreasing. 2. If we walk from left to right along a line passing through distinct points P and Q, then we will experience a constant steepness equal to the slope of the line.
    [Show full text]