DOCSLIB.ORG

First-Order Differential Equations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
First-Order Differential Equations Chapter FIRST-ORDER 16 DIFFERENTIAL EQUATIONS OVERVIEW In Section 4.7 we introduced differential equations of the form dy dx = ƒ(x), > where ƒ is given and y is an unknown function of x. When ƒ is continuous over some inter- val, we found the general solution y(x) by integration, y = 1ƒ(x) dx . In Section 7.5 we solved separable differential equations. Such equations arise when investigating exponen- tial growth or decay, for example. In this chapter we study some other types of first-order differential equations. They involve only first derivatives of the unknown function. 16.1 Solutions, Slope Fields, and Picard’s Theorem We begin this section by defining general differential equations involving first derivatives. We then look at slope fields, which give a geometric picture of the solutions to such equa- tions. Finally we present Picard’s Theorem, which gives conditions under which first-order differential equations have exactly one solution. General First-Order Differential Equations and Solutions A first-order differential equation is an equation dy = ƒsx, yd (1) dx in which ƒ(x, y) is a function of two variables defined on a region in the xy-plane. The equation is of first order because it involves only the first derivative dy dx (and not > higher-order derivatives). We point out that the equations d y¿=ƒsx, yd and y = ƒsx, yd dx are equivalent to Equation (1) and all three forms will be used interchangeably in the text. A solution of Equation (1) is a differentiable function y = ysxd defined on an interval I of x-values (perhaps infinite) such that d ysxd = ƒsx, ysxdd dx on that interval. That is, when y(x) and its derivative y¿sxd are substituted into Equation (1), the resulting equation is true for all x over the interval I. The general solution to a first- order differential equation is a solution that contains all possible solutions. The general 16-1 16-2 Chapter 16: First-Order Differential Equations solution always contains an arbitrary constant, but having this property doesn’t mean a solution is the general solution. That is, a solution may contain an arbitrary constant with- out being the general solution. Establishing that a solution is the general solution may re- quire deeper results from the theory of differential equations and is best studied in a more advanced course. EXAMPLE 1 Show that every member of the family of functions = C + y x 2 is a solution of the first-order differential equation dy 1 = s2 - yd dx x on the interval s0, q d, where C is any constant. Solution Differentiating y = C x + 2 gives > dy d 1 C = C + 0 =- . dx dx ax b x2 Thus we need only verify that for all x H s0, q d, C 1 C - = 2 - + 2 . x2 x c a x bd This last equation follows immediately by expanding the expression on the right-hand side: 1 C 1 C C 2 - + 2 = - =- . x c a x bd x a x b x2 Therefore, for every value of C, the function y = C x + 2 is a solution of the differential > equation. As was the case in finding antiderivatives, we often need a particular rather than the general solution to a first-order differential equation y¿=ƒsx, yd.The particular solution satisfying the initial condition ysx0d = y0 is the solution y = ysxd whose value is y0 when x = x0. Thus the graph of the particular solution passes through the point sx0 , y0d in the xy-plane. A first-order initial value problem is a differential equation y¿=ƒsx, yd whose solution must satisfy an initial condition ysx0d = y0. EXAMPLE 2 Show that the function 1 y = sx + 1d - ex 3 is a solution to the first-order initial value problem dy 2 = y - x, ys0d = . dx 3 Solution The equation dy = y - x dx is a first-order differential equation with ƒsx, yd = y - x. 16.1 Solutions, Slope Fields, and Picard’s Theorem 16-3 y On the left side of the equation: y ϭ (x ϩ 1) 1 ex 2 2 3 0, dy d 1 x 1 x 3 1 = x + 1 - e = 1 - e . dx dx a 3 b 3 x –4 –2 2 4 –1 On the right side of the equation: –2 1 1 y - x = sx + 1d - ex - x = 1 - ex . –3 3 3 –4 The function satisfies the initial condition because FIGURE 16.1 Graph of the solution 1 1 2 ys0d = sx + 1d - ex = 1 - = . 1 c 3 d = 3 3 y = sx + 1d - ex to the differential x 0 3 equation dy dx = y - x, with initial The graph of the function is shown in Figure 16.1. > 2 condition ys0d = (Example 2). 3 Slope Fields: Viewing Solution Curves Each time we specify an initial condition ysx0d = y0 for the solution of a differential equa- tion y¿=ƒsx, yd, the solution curve (graph of the solution) is required to pass through the point sx0 , y0d and to have slope ƒsx0 , y0d there. We can picture these slopes graphically by drawing short line segments of slope ƒ(x, y) at selected points (x, y) in the region of the xy-plane that constitutes the domain of ƒ. Each segment has the same slope as the solution curve through (x, y) and so is tangent to the curve there. The resulting picture is called a slope field (or direction field) and gives a visualization of the general shape of the solu- tion curves. Figure 16.2a shows a slope field, with a particular solution sketched into it in Figure 16.2b. We see how these line segments indicate the direction the solution curve takes at each point it passes through. 2 y y 0, 3 4 4 2 2 x x –4–2 02 4 –4–2 02 4 –2 –2 –4 –4 (a) (b) dy FIGURE 16.2 (a) Slope field for = y - x. (b) The particular solution dx 2 curve through the point 0, (Example 2). a 3 b Figure 16.3 shows three slope fields and we see how the solution curves behave by following the tangent line segments in these fields. 16-4 Chapter 16: First-Order Differential Equations 2xy (a) y' ϭ y Ϫ x2 (b) y' ϭ – (c) y' ϭ (1 Ϫ x)y ϩ x 1 ϩ x2 2 FIGURE 16.3 Slope fields (top row) and selected solution curves (bottom row). In computer renditions, slope segments are sometimes portrayed with arrows, as they are here. This is not to be taken as an indication that slopes have directions, however, for they do not. Constructing a slope field with pencil and paper can be quite tedious. All our exam- ples were generated by a computer. The Existence of Solutions A basic question in the study of first-order initial value problems concerns whether a solu- tion even exists. A second important question asks whether there can be more than one so- lution. Some conditions must be imposed to assure the existence of exactly one solution, as illustrated in the next example. EXAMPLE 3 The initial value problem dy 4 5 = y > , y(0) = 0 dx has more than one solution. One solution is the constant function y(x) = 0 for which the y graph lies along the x-axis. A second solution is found by separating variables and inte- (7, 5.4) grating, as we did in Section 7.5. This leads to 5 x 5 y = . a5 b 1 (5, 1) 5 x The two solutions y = 0 and y = (x 5) both satisfy the initial condition y(0) = 0 –5 5 > (–5, –1) –1 (Figure 16.4). We have found a differential equation with multiple solutions satisfying the same ini- tial condition. This differential equation has even more solutions. For instance, two addi- –5 tional solutions are 0, for x … 0 FIGURE 16.4 The graph of the solution 5 5 y = x y = (x 5) to the initial value problem in ,forx 7 0 > • 5 Example 3. Another solution is y = 0. a b 16.1 Solutions, Slope Fields, and Picard’s Theorem 16-5 and x 5 ,forx … 0 y = a5 b . • 0, for x 7 0 In many applications it is desirable to know that there is exactly one solution to an ini- tial value problem. Such a solution is said to be unique. Picard’s Theorem gives conditions under which there is precisely one solution. It guarantees both the existence and unique- ness of a solution. THEOREM 1—Picard’s Theorem Suppose that both ƒ(x, y) and its partial derivative 0ƒ 0y are continuous on the interior of a rectangle R, and that (x , y ) is > 0 0 an interior point of R. Then the initial value problem dy = ƒ(x, y), y(x ) = y (2) dx 0 0 has a unique solution y ϭ y(x) for x in some open interval containing x0. The differential equation in Example 3 fails to satisfy the conditions of Picard’s Theorem. 4 5 Although the function ƒ(x, y) = y > from Example 3 is continuous in the entire xy-plane, -1 5 the partial derivative 0ƒ 0y = (4 5) y > fails to be continuous at the point (0, 0) speci- > > fied by the initial condition. Thus we found the possibility of more than one solution to the given initial value problem. Moreover, the partial derivative 0ƒ 0y is not even defined > where y = 0. However, the initial value problem of Example 3 does have unique solutions whenever the initial condition y(x0) = y0 has y0 Z 0.
Load more

Recommended publications
  • Handout of Differential Equations
    HANDOUT DIFFERENTIAL EQUATIONS For International Class Nikenasih Binatari NIP. 19841019 200812 2 005 Mathematics Educational Department Faculty of Mathematics and Natural Sciences State University of Yogyakarta 2010 CONTENTS Cover Contents I. Introduction to Differential Equations - Some basic mathematical models………………………………… 1 - Definitions and terminology……………………………………… 3 - Classification of Differential Equation……………………………. 7 - Initial Value Problems…………………………………………….. 9 - Boundary Value Problems………………………………………... 10 - Autonomous Equation……………………………………………. 11 - Definition of Differential Equation Solutions……………………... 16 II. First Order Equations for which exact solutions are obtainable - Standart forms of first order Differential Equation………………. 19 - Exact Equation…………………………………………………….. 20 - Solution of exact differential equations…………………………... 22 - Method of grouping………………………………………………. 25 - Integrating factor………………………………………………….. 26 - Separable differential equations…………………………………... 28 - Homogeneous differential equations……………………………... 31 - Linear differential Equations……………………………………… 34 - Bernoulli differential equations…………………………………… 36 - Special integrating factor………………………………………….. 39 - Special transformations…………………………………………… 40 III. Application of first order equations - Orthogonal trajectories…………………………………………... 43 - Oblique trajectories………………………………………………. 46 - Application in mechanics problems and rate problems………….. 48 IV. Explicit methods of solving higher order linear differential equations - Basic theory of linear differential
    [Show full text]
  • Ordinary Differential Equation 2
    Unit - II Linear Systems- Let us consider a system of first order differential equations of the form dx = F(,)x y dt (1) dy = G(,)x y dt Where t is an independent variable. And x & y are dependent variables. The system (1) is called a linear system if both F(x, y) and G(x, y) are linear in x and y. dx = a ()t x + b ()t y + f() t dt 1 1 1 Also system (1) can be written as (2) dy = a ()t x + b ()t y + f() t dt 2 2 2 ∀ = [ ] Where ai t)( , bi t)( and fi () t i 2,1 are continuous functions on a, b . Homogeneous and Non-Homogeneous Linear Systems- The system (2) is called a homogeneous linear system, if both f1 ( t )and f2 ( t ) are identically zero and if both f1 ( t )and f2 t)( are not equal to zero, then the system (2) is called a non-homogeneous linear system. x = x() t Solution- A pair of functions defined on [a, b]is said to be a solution of (2) if it satisfies y = y() t (2). dx = 4x − y ........ A dt Example- (3) dy = 2x + y ........ B dt dx d 2 x dx From A, y = 4x − putting in B we obtain − 5 + 6x = 0is a 2 nd order differential dt dt 2 dt x = e2t equation. The auxiliary equation is m2 − 5m + 6 = 0 ⇒ m = 3,2 so putting x = e2t in A, we x = e3t obtain y = 2e2t again putting x = e3t in A, we obtain y = e3t .
    [Show full text]
  • Ordinary Differential Equations
    Ordinary Differential Equations for Engineers and Scientists Gregg Waterman Oregon Institute of Technology c 2017 Gregg Waterman This work is licensed under the Creative Commons Attribution 4.0 International license. The essence of the license is that You are free to: Share copy and redistribute the material in any medium or format • Adapt remix, transform, and build upon the material for any purpose, even commercially. • The licensor cannot revoke these freedoms as long as you follow the license terms. Under the following terms: Attribution You must give appropriate credit, provide a link to the license, and indicate if changes • were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use. No additional restrictions You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits. Notices: You do not have to comply with the license for elements of the material in the public domain or where your use is permitted by an applicable exception or limitation. No warranties are given. The license may not give you all of the permissions necessary for your intended use. For example, other rights such as publicity, privacy, or moral rights may limit how you use the material. For any reuse or distribution, you must make clear to others the license terms of this work. The best way to do this is with a link to the web page below. To view a full copy of this license, visit https://creativecommons.org/licenses/by/4.0/legalcode.
    [Show full text]
  • Phase Plane Diagrams of Difference Equations
    PHASE PLANE DIAGRAMS OF DIFFERENCE EQUATIONS TANYA DEWLAND, JEROME WESTON, AND RACHEL WEYRENS Abstract. We will be determining qualitative features of a dis- crete dynamical system of homogeneous difference equations with constant coefficients. By creating phase plane diagrams of our system we can visualize these features, such as convergence, equi- librium points, and stability. 1. Introduction Continuous systems are often approximated as discrete processes, mean- ing that we look only at the solutions for positive integer inputs. Dif- ference equations are recurrence relations, and first order difference equations only depend on the previous value. Using difference equa- tions, we can model discrete dynamical systems. The observations we can determine, by analyzing phase plane diagrams of difference equa- tions, are if we are modeling decay or growth, convergence, stability, and equilibrium points. For this paper, we will only consider two dimensional systems. Suppose x(k) and y(k) are two functions of the positive integers that satisfy the following system of difference equations: x(k + 1) = ax(k) + by(k) y(k + 1) = cx(k) + dy(k): This system is more simply written in matrix from z(k + 1) = Az(k); x(k) a b where z(k) = is a column vector and A = . If z(0) = z y(k) c d 0 is the initial condition then the solution to the initial value prob- lem z(k + 1) = Az(k); z(0) = z0; 1 2 TANYA DEWLAND, JEROME WESTON, AND RACHEL WEYRENS is k z(k) = A z0: Each z(k) is represented as a point (x(k); y(k)) in the Euclidean plane.
    [Show full text]
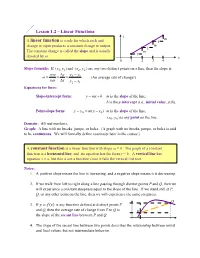
  • Lesson 1.2 – Linear Functions Y M a Linear Function Is a Rule for Which Each Unit 1 Change in Input Produces a Constant Change in Output
    Lesson 1.2 – Linear Functions y m A linear function is a rule for which each unit 1 change in input produces a constant change in output. m 1 The constant change is called the slope and is usually m 1 denoted by m. x 0 1 2 3 4 Slope formula: If (x1, y1)and (x2 , y2 ) are any two distinct points on a line, then the slope is rise y y y m 2 1 . (An average rate of change!) run x x x 2 1 Equations for lines: Slope-intercept form: y mx b m is the slope of the line; b is the y-intercept (i.e., initial value, y(0)). Point-slope form: y y0 m(x x0 ) m is the slope of the line; (x0, y0 ) is any point on the line. Domain: All real numbers. Graph: A line with no breaks, jumps, or holes. (A graph with no breaks, jumps, or holes is said to be continuous. We will formally define continuity later in the course.) A constant function is a linear function with slope m = 0. The graph of a constant function is a horizontal line, and its equation has the form y = b. A vertical line has equation x = a, but this is not a function since it fails the vertical line test. Notes: 1. A positive slope means the line is increasing, and a negative slope means it is decreasing. 2. If we walk from left to right along a line passing through distinct points P and Q, then we will experience a constant steepness equal to the slope of the line.
    [Show full text]
  • New Dirac Delta Function Based Methods with Applications To
    New Dirac Delta function based methods with applications to perturbative expansions in quantum field theory Achim Kempf1, David M. Jackson2, Alejandro H. Morales3 1Departments of Applied Mathematics and Physics 2Department of Combinatorics and Optimization University of Waterloo, Ontario N2L 3G1, Canada, 3Laboratoire de Combinatoire et d’Informatique Math´ematique (LaCIM) Universit´edu Qu´ebec `aMontr´eal, Canada Abstract. We derive new all-purpose methods that involve the Dirac Delta distribution. Some of the new methods use derivatives in the argument of the Dirac Delta. We highlight potential avenues for applications to quantum field theory and we also exhibit a connection to the problem of blurring/deblurring in signal processing. We find that blurring, which can be thought of as a result of multi-path evolution, is, in Euclidean quantum field theory without spontaneous symmetry breaking, the strong coupling dual of the usual small coupling expansion in terms of the sum over Feynman graphs. arXiv:1404.0747v3 [math-ph] 23 Sep 2014 2 1. A method for generating new representations of the Dirac Delta The Dirac Delta distribution, see e.g., [1, 2, 3], serves as a useful tool from physics to engineering. Our aim here is to develop new all-purpose methods involving the Dirac Delta distribution and to show possible avenues for applications, in particular, to quantum field theory. We begin by fixing the conventions for the Fourier transform: 1 1 g(y) := g(x) eixy dx, g(x)= g(y) e−ixy dy (1) √2π √2π Z Z To simplify the notation we denote integration over the real line by the absence of e e integration delimiters.
    [Show full text]
  • Modifications of the Method of Variation of Parameters
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector International Joumal Available online at www.sciencedirect.com computers & oc,-.c~ ~°..-cT- mathematics with applications Computers and Mathematics with Applications 51 (2006) 451-466 www.elsevier.com/locate/camwa Modifications of the Method of Variation of Parameters ROBERTO BARRIO* GME, Depto. Matem~tica Aplicada Facultad de Ciencias Universidad de Zaragoza E-50009 Zaragoza, Spain rbarrio@unizar, es SERGIO SERRANO GME, Depto. MatemAtica Aplicada Centro Politdcnico Superior Universidad de Zaragoza Maria de Luna 3, E-50015 Zaragoza, Spain sserrano©unizar, es (Received February PO05; revised and accepted October 2005) Abstract--ln spite of being a classical method for solving differential equations, the method of variation of parameters continues having a great interest in theoretical and practical applications, as in astrodynamics. In this paper we analyse this method providing some modifications and generalised theoretical results. Finally, we present an application to the determination of the ephemeris of an artificial satellite, showing the benefits of the method of variation of parameters for this kind of problems. ~) 2006 Elsevier Ltd. All rights reserved. Keywords--Variation of parameters, Lagrange equations, Gauss equations, Satellite orbits, Dif- ferential equations. 1. INTRODUCTION The method of variation of parameters was developed by Leonhard Euler in the middle of XVIII century to describe the mutual perturbations of Jupiter and Saturn. However, his results were not absolutely correct because he did not consider the orbital elements varying simultaneously. In 1766, Lagrange improved the method developed by Euler, although he kept considering some of the orbital elements as constants, which caused some of his equations to be incorrect.
    [Show full text]
  • Phase Plane Methods
    Chapter 10 Phase Plane Methods Contents 10.1 Planar Autonomous Systems . 680 10.2 Planar Constant Linear Systems . 694 10.3 Planar Almost Linear Systems . 705 10.4 Biological Models . 715 10.5 Mechanical Models . 730 Studied here are planar autonomous systems of differential equations. The topics: Planar Autonomous Systems: Phase Portraits, Stability. Planar Constant Linear Systems: Classification of isolated equilib- ria, Phase portraits. Planar Almost Linear Systems: Phase portraits, Nonlinear classi- fications of equilibria. Biological Models: Predator-prey models, Competition models, Survival of one species, Co-existence, Alligators, doomsday and extinction. Mechanical Models: Nonlinear spring-mass system, Soft and hard springs, Energy conservation, Phase plane and scenes. 680 Phase Plane Methods 10.1 Planar Autonomous Systems A set of two scalar differential equations of the form x0(t) = f(x(t); y(t)); (1) y0(t) = g(x(t); y(t)): is called a planar autonomous system. The term autonomous means self-governing, justified by the absence of the time variable t in the functions f(x; y), g(x; y). ! ! x(t) f(x; y) To obtain the vector form, let ~u(t) = , F~ (x; y) = y(t) g(x; y) and write (1) as the first order vector-matrix system d (2) ~u(t) = F~ (~u(t)): dt It is assumed that f, g are continuously differentiable in some region D in the xy-plane. This assumption makes F~ continuously differentiable in D and guarantees that Picard's existence-uniqueness theorem for initial d ~ value problems applies to the initial value problem dt ~u(t) = F (~u(t)), ~u(0) = ~u0.
    [Show full text]
  • Calculus and Differential Equations II
    Calculus and Differential Equations II MATH 250 B Linear systems of differential equations Linear systems of differential equations Calculus and Differential Equations II Second order autonomous linear systems We are mostly interested with2 × 2 first order autonomous systems of the form x0 = a x + b y y 0 = c x + d y where x and y are functions of t and a, b, c, and d are real constants. Such a system may be re-written in matrix form as d x x a b = M ; M = : dt y y c d The purpose of this section is to classify the dynamics of the solutions of the above system, in terms of the properties of the matrix M. Linear systems of differential equations Calculus and Differential Equations II Existence and uniqueness (general statement) Consider a linear system of the form dY = M(t)Y + F (t); dt where Y and F (t) are n × 1 column vectors, and M(t) is an n × n matrix whose entries may depend on t. Existence and uniqueness theorem: If the entries of the matrix M(t) and of the vector F (t) are continuous on some open interval I containing t0, then the initial value problem dY = M(t)Y + F (t); Y (t ) = Y dt 0 0 has a unique solution on I . In particular, this means that trajectories in the phase space do not cross. Linear systems of differential equations Calculus and Differential Equations II General solution The general solution to Y 0 = M(t)Y + F (t) reads Y (t) = C1 Y1(t) + C2 Y2(t) + ··· + Cn Yn(t) + Yp(t); = U(t) C + Yp(t); where 0 Yp(t) is a particular solution to Y = M(t)Y + F (t).
    [Show full text]
  • Second Order Linear Differential Equations Y
    Second Order Linear Differential Equations Second order linear equations with constant coefficients; Fundamental solutions; Wronskian; Existence and Uniqueness of solutions; the characteristic equation; solutions of homogeneous linear equations; reduction of order; Euler equations In this chapter we will study ordinary differential equations of the standard form below, known as the second order linear equations : y″ + p(t) y′ + q(t) y = g(t). Homogeneous Equations : If g(t) = 0, then the equation above becomes y″ + p(t) y′ + q(t) y = 0. It is called a homogeneous equation. Otherwise, the equation is nonhomogeneous (or inhomogeneous ). Trivial Solution : For the homogeneous equation above, note that the function y(t) = 0 always satisfies the given equation, regardless what p(t) and q(t) are. This constant zero solution is called the trivial solution of such an equation. © 2008, 2016 Zachary S Tseng B-1 - 1 Second Order Linear Homogeneous Differential Equations with Constant Coefficients For the most part, we will only learn how to solve second order linear equation with constant coefficients (that is, when p(t) and q(t) are constants). Since a homogeneous equation is easier to solve compares to its nonhomogeneous counterpart, we start with second order linear homogeneous equations that contain constant coefficients only: a y″ + b y′ + c y = 0. Where a, b, and c are constants, a ≠ 0. A very simple instance of such type of equations is y″ − y = 0 . The equation’s solution is any function satisfying the equality t y″ = y. Obviously y1 = e is a solution, and so is any constant multiple t −t of it, C1 e .
    [Show full text]
  • 9 Power and Polynomial Functions
    Arkansas Tech University MATH 2243: Business Calculus Dr. Marcel B. Finan 9 Power and Polynomial Functions A function f(x) is a power function of x if there is a constant k such that f(x) = kxn If n > 0, then we say that f(x) is proportional to the nth power of x: If n < 0 then f(x) is said to be inversely proportional to the nth power of x. We call k the constant of proportionality. Example 9.1 (a) The strength, S, of a beam is proportional to the square of its thickness, h: Write a formula for S in terms of h: (b) The gravitational force, F; between two bodies is inversely proportional to the square of the distance d between them. Write a formula for F in terms of d: Solution. 2 k (a) S = kh ; where k > 0: (b) F = d2 ; k > 0: A power function f(x) = kxn , with n a positive integer, is called a mono- mial function. A polynomial function is a sum of several monomial func- tions. Typically, a polynomial function is a function of the form n n−1 f(x) = anx + an−1x + ··· + a1x + a0; an 6= 0 where an; an−1; ··· ; a1; a0 are all real numbers, called the coefficients of f(x): The number n is a non-negative integer. It is called the degree of the polynomial. A polynomial of degree zero is just a constant function. A polynomial of degree one is a linear function, of degree two a quadratic function, etc. The number an is called the leading coefficient and a0 is called the constant term.
    [Show full text]
  • Polynomials.Pdf
    POLYNOMIALS James T. Smith San Francisco State University For any real coefficients a0,a1,...,an with n $ 0 and an =' 0, the function p defined by setting n p(x) = a0 + a1 x + AAA + an x for all real x is called a real polynomial of degree n. Often, we write n = degree p and call an its leading coefficient. The constant function with value zero is regarded as a real polynomial of degree –1. For each n the set of all polynomials with degree # n is closed under addition, subtraction, and multiplication by scalars. The algebra of polynomials of degree # 0 —the constant functions—is the same as that of real num- bers, and you need not distinguish between those concepts. Polynomials of degrees 1 and 2 are called linear and quadratic. Polynomial multiplication Suppose f and g are nonzero polynomials of degrees m and n: m f (x) = a0 + a1 x + AAA + am x & am =' 0, n g(x) = b0 + b1 x + AAA + bn x & bn =' 0. Their product fg is a nonzero polynomial of degree m + n: m+n f (x) g(x) = a 0 b 0 + AAA + a m bn x & a m bn =' 0. From this you can deduce the cancellation law: if f, g, and h are polynomials, f =' 0, and fg = f h, then g = h. For then you have 0 = fg – f h = f ( g – h), hence g – h = 0. Note the analogy between this wording of the cancellation law and the corresponding fact about multiplication of numbers. One of the most useful results about integer multiplication is the unique factoriza- tion theorem: for every integer f > 1 there exist primes p1 ,..., pm and integers e1 em e1 ,...,em > 0 such that f = pp1 " m ; the set consisting of all pairs <pk , ek > is unique.
    [Show full text]