DOCSLIB.ORG

Herald of the NEFU T.10 №3. 2013

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Herald of the NEFU T.10 №3. 2013 CONTENT PHYSICAL AND MATHEMATICAL SCIENCES Vabishchev P. N., Vasilieva M. V. Numerical simulation of thermoelasticity problem.....................................................................................3 BIOLOGICAL SCIENCES Pesterev A. P. Soil covering in the West of Yakutia.........................................................................................................................................8 Sviridenko B. F., Efremov A. N., Sviridenko T. V. New to the algal fl ora of the Republic of Sakha (Yakutia) macroscopic algae species (Zygnematales, Vaucheriales).........................................................................................................................................................................15 GEOLOGICAL AND MINERALOGICAL SCIENCES Dmitriev E. P., Pomortsev O. A., Tretyakov M. F., Popov V. F., Loskutov E. E., Vasilyeva O. I. Peculiarities of the geomorphological structure of the river West Khandyga upstream............................................................................................................................................20 . ECONOMIC SCIENCES Mezhakov V. Z., Serebrennikov V. I., Akhremenko T. V. Regional aspects of the land use and the administrative region’s land resources protection........................................................................................................................................................................................................27 Okorokov A. I. About the condition and development of house northern reindeer farming in the Republic of Sakha (Yakutia).................33 PHILOSOPHIC SCIENCES Ievlev E. K. A. I. Sofronov and spiritual humanism.......................................................................................................................................38 PHILOLOGICAL SCIENCES Dorzhu Ch. M. Revisiting the origin of the prosodic phenomenon in the phonological system of Tuvinian language.................................43 Ivanov V. N. Revisiting of comparative-historical study of olonkho and the epos of Turkic people..............................................................48 Ivanova N. I. The linguistic status of the Russian language in the Republic of Sakha (Yakutia).................................................................53 Malysheva N. V. Lexical-semantic parallels of Yakut and Uigur languages (nouns).....................................................................................58 Myreeva A. N. The philosophic novel in the Yakut prose of 1990th years of the XX th century...................................................................63 Nikaeva Т. М. Ethnic stereotypes in the worldview of Russians, Yakuts, Evenks and Evens........................................................................68 Orosina N. A. Collective activity of the Tattinsky intelligence on the folklore at the end of the XIX century (on the materials of the branch of Saint-Petersburg Archive of RAS).................................................................................................................................................75 Rysbekova S. T. Katanov N. F.: about Turkic roots in Uryankhai and Kazakh languages.............................................................................79 Sizykh O. V. Allusive nature of the story by L. S. Petrushevskaya «Outburst»..............................................................................................82 PEDAGOGICAL SCIENCES Böhm J. Learning as a capacious phenomenon – the example scool meal....................................................................................................86 Vinokurov A. A., Nogovitsyn R. R., Khazankovich Yu. G. Intellectual property management: problems and prospects (from the experience of the NEFU named after M. K. Ammosov)................................................................................................................90 Egorov V. N. Social-pedagogical peculiarities of educational process organization at schools of indigenous peoples of the North.............95 Ekeeva E. V. Traditions of physical upbringing in an Altai family.................................................................................................................98 Ivanova A. V., Prokopyev A. A. Interdisciplinary informational-mathematical competence as a factor of improvement of the quality of lawyers professional training in the conditions of the higher education modernization..............................................................................101 Shemanaev V. K. To the issue of substantiation of professional-pedagogical system of multilevel training of instructors-conductors of sport health-giving tourism......................................................................................................................................................................106 1 ВЕСТНИК СВФУ, 2010, том 7, № 4 MEDICAL SCIENCES Varfolomeeva N. A., Bushkova E. A., Sydykova L. A., Kuzmina A. A., Malogulova I. Sh., Abramova Ya. I. Pharmacotherapy adherence under diabetes mellitus type II in the Republic of Sakha (Yakutia).............................................................................................................111 Ushnitsky I. D., Rogaleva A. S., Belchusova E. A., Ammosova V. N., Petrova N. N., Sheina N. E. The composition and properties of mixed saliva of elderly people living on high latitude............................................................................................................................................115 CHRONICLE Vasiliev V. I., Pavlova N. V. Results of the 2nd International conference on Supercomputer Technologies of Mathematical Modelling.....119 ANNIVERSARIES Arkhipova. S. N. In hallowed memory of Anna Vasilievna Mordovskaya (1958-2012)...............................................................................121 2 PHYSICAL AND MATHEMATICAL SCIENCES UDC 519.63 P. N. Vabishchevich, V. M. Vasilieva Numerical Simulation of Thermoelasticity Problem The paper considers the coupled quasi-stationary linear system of equations for temperature and displacement, describing the thermoelastic behavior of the body. The stability estimates of the studied differential problem are presented. For the numerical solution, we approximate our system using the fi nite elements method, and for approximation by time we use the standard two-layer weighted schemes. The discrete problem has proven stable. The results of the numerical simulation of the model problem of thermoelasticity are presented. Key words: strain-stress state, thermoelasticity, Lame s equation, heat conduction equation, differential and operator equations system, two-layer weighted schemes, stability estimates, a priori estimate, fi nite elements method, numerical simulation. Many applied problems mathematical simulation are quasistationary problem (stationary for displacements and related to the need to calculate the strain-stress state of non-stationary for temperature) can be solved through the solids. In many cases, deformations are caused by use of two-layer weighted scheme [9]. The approximate thermal dilation. To study the deformations, the models of solution for the initial data and the right-hand side under thermoelasticity are used [1-4]. standard weight limits has proven absolutely stable. The basic mathematical models of thermoelasticity We have obtained priori estimate of the approximate include Lame equation for displacements and the heat solution, which is consistent with the corresponding equation. The fundamental point is that the system estimate for the solution of the differential problem. The of equations is tied up: the equation for displacement possibilities of computational algorithm are illustrated comprises volume force proportional to the temperature by the computed data on the model two-dimensional gradient and the temperature equation includes a term problem for the body of rectangular cross section with a describing the compressibility of the medium. circular cutout. In this paper, we describe a computational algorithm Problem statement. From mechanical and heat for solving problems of thermoelasticity. It is based impacts, displacement u, deformation ε and stress σ on the fi nite element approximation of the temperature fi elds occur in the elastic body. Suppose T – constant fi eld and the displacement fi eld in space [5-8]. The absolute temperature at which the body is in an initial equilibrium state, and θ – the temperature increment. Mechanical impact on the body shall mean the impact VABISHCHEVICH Pyotr Nikolaevich – Doctor of Physical of outside forces (volume or surface ones), and heat and Mathematical Sciences, Professor , Head of laboratory of impact shall mean the heat exchange processes between the Institute of Problems of the Safe Development of Nuclear the surface of the body and the environment, and release Power RAS, Leading Scientist-Academic Advisor of the North- or absorption of heat by the sources inside the body. Eastern Federal University named after M.K. Ammosov. The simulation model of the thermoelastic behavior E-mail: [email protected] of the body is described by the coupled system of VASILIEVA Maria Vasilievna – Candidate of Physical and equations for displacements u and the temperature Mathematical Sciences, Chairman of the Department of Parallel increment θ in the system Ω: Technologies of the Center of Computational Technologies ≤°§§© ≤°§ of the Institute of Mathematics and Informatics of the North- ≤°§§© ≤°§ (1)
Load more

Recommended publications
  • Northern Sea Route Cargo Flows and Infrastructure- Present State And
    Northern Sea Route Cargo Flows and Infrastructure – Present State and Future Potential By Claes Lykke Ragner FNI Report 13/2000 FRIDTJOF NANSENS INSTITUTT THE FRIDTJOF NANSEN INSTITUTE Tittel/Title Sider/Pages Northern Sea Route Cargo Flows and Infrastructure – Present 124 State and Future Potential Publikasjonstype/Publication Type Nummer/Number FNI Report 13/2000 Forfatter(e)/Author(s) ISBN Claes Lykke Ragner 82-7613-400-9 Program/Programme ISSN 0801-2431 Prosjekt/Project Sammendrag/Abstract The report assesses the Northern Sea Route’s commercial potential and economic importance, both as a transit route between Europe and Asia, and as an export route for oil, gas and other natural resources in the Russian Arctic. First, it conducts a survey of past and present Northern Sea Route (NSR) cargo flows. Then follow discussions of the route’s commercial potential as a transit route, as well as of its economic importance and relevance for each of the Russian Arctic regions. These discussions are summarized by estimates of what types and volumes of NSR cargoes that can realistically be expected in the period 2000-2015. This is then followed by a survey of the status quo of the NSR infrastructure (above all the ice-breakers, ice-class cargo vessels and ports), with estimates of its future capacity. Based on the estimated future NSR cargo potential, future NSR infrastructure requirements are calculated and compared with the estimated capacity in order to identify the main, future infrastructure bottlenecks for NSR operations. The information presented in the report is mainly compiled from data and research results that were published through the International Northern Sea Route Programme (INSROP) 1993-99, but considerable updates have been made using recent information, statistics and analyses from various sources.
    [Show full text]
  • Structure, Condition, and Prospects of Electrical Grids in the Republic of Sakha (Yakutia)
    E3S Web of Conferences 124, 04001 (2019) https://doi.org/10.1051/e3sconf/201912404001 SES-2019 Structure, condition, and prospects of electrical grids in the Republic of Sakha (Yakutia) N. S. Volotkovskaya1, N. N. Kugusheva1,2, A. S. Semenov1,2,*, I. A. Yakushev1,2, S. N. Pavlova1,3, and O. V. Kolosova4 1 North-Eastern Federal University n.a. M.K. Ammosov, Polytechnic Institute (branch) in Mirny, Sakha (Yakutia), Russia 2 North-Eastern Federal University n.a. M.K. Ammosov, Institute of Mathematics and Information Science, Sakha (Yakutia), Russia 3 North-Eastern Federal University n.a. M.K. Ammosov, Institute of Finances and Economics, Sakha (Yakutia), Russia 4 Peter the Great St. Petersburg Polytechnic University, St Petersburg, Russia Abstract. The paper analyzes the condition of electrical grids in the west of the Republic of Sakha (Yakutia); data sampled for the last 10 years. It demonstrates the geographic location of grids, which defines the scale of the study. Technical indicators are presented for 10 years; they reflect an increase in the fixed assets. The paper derives mathematical models of the wear of transmission equipment used in the western grids. It proves that the condition of equipment will deteriorate further unless its maintenance is properly funded. The paper analyzes the prospects of electrical grids in the Republic of Sakha (Yakutia). It presents a program for local energy optimization. The costs associated with five alternative development scenarios are calculated and presented in a tabular format. 1 Introduction 30% of the total heat in the Republic. HPPs account for 37.5% of the installed capacity.
    [Show full text]
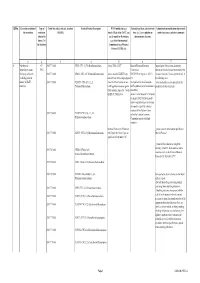
  • Qrno. 1 2 3 4 5 6 7 1 CP 2903 77 100 0 Cfcl3
    QRNo. General description of Type of Tariff line code(s) affected, based on Detailed Product Description WTO Justification (e.g. National legal basis and entry into Administration, modification of previously the restriction restriction HS(2012) Article XX(g) of the GATT, etc.) force (i.e. Law, regulation or notified measures, and other comments (Symbol in and Grounds for Restriction, administrative decision) Annex 2 of e.g., Other International the Decision) Commitments (e.g. Montreal Protocol, CITES, etc) 12 3 4 5 6 7 1 Prohibition to CP 2903 77 100 0 CFCl3 (CFC-11) Trichlorofluoromethane Article XX(h) GATT Board of Eurasian Economic Import/export of these ozone destroying import/export ozone CP-X Commission substances from/to the customs territory of the destroying substances 2903 77 200 0 CF2Cl2 (CFC-12) Dichlorodifluoromethane Article 46 of the EAEU Treaty DECISION on August 16, 2012 N Eurasian Economic Union is permitted only in (excluding goods in dated 29 may 2014 and paragraphs 134 the following cases: transit) (all EAEU 2903 77 300 0 C2F3Cl3 (CFC-113) 1,1,2- 4 and 37 of the Protocol on non- On legal acts in the field of non- _to be used solely as a raw material for the countries) Trichlorotrifluoroethane tariff regulation measures against tariff regulation (as last amended at 2 production of other chemicals; third countries Annex No. 7 to the June 2016) EAEU of 29 May 2014 Annex 1 to the Decision N 134 dated 16 August 2012 Unit list of goods subject to prohibitions or restrictions on import or export by countries- members of the
    [Show full text]
  • Terminal Evaluation of the UNEP/GEF Project
    United Nations Environment Programme Terminal Evaluation of the UNEP/GEF Project “Russian Federation – Support to the National Programme of Action for the Protection of the Arctic Marine Environment” Prof. Dr. Ivan Holoubek & Oleg Sutkaitis UNEP Evaluation Office September 2012 Table of Contents Project Identification Table _________________________________________________ i Executive summary ________________________________________________________ ii 1. Evaluation background ________________________________________________ 1 A. Context _____________________________________________________________________________ 1 B. The Project __________________________________________________________________________ 2 C. Evaluation objectives, scope and methodology ____________________________________________ 4 C. 1 Objective and Scope of the Evaluation ________________________________________________ 4 C. 2 Overall Approach and Methods ______________________________________________________ 4 C. 3. Limitations and Constraints ________________________________________________________ 5 2. Project performance and impact ___________________________________________ 6 A. Attainment of objectives and planned results ___________________________________ 6 A.1 Achievement of outputs and activities __________________________________________________ 6 A.2 Relevance __________________________________________________________________________ 7 A. 3 Effectiveness _______________________________________________________________________ 9 A.4 Efficiency _________________________________________________________________________
    [Show full text]
  • Goldman Et Al. (2016) Monitoring of the Ecological Security in the North-Western Region of the Republic …
    ISSN 2056-9386 Volume 3 (2016) issue 3, article 2 Monitoring of the ecological security in the north- western region of the Republic of Sakha, Russian Federation 俄罗斯联邦萨哈共和国西北地区的生态安全监测 Albina A. Goldman, Elena V. Sleptsova, Raissa P. Ivanova Mirny Polytechnic Institute (branch) of Ammosov North-Eastern Federal University (NEFU), Mirny, Tikhonova street 5, build.1, Russian Federation [email protected], [email protected], [email protected] Accepted for publication on 3rd September 2016 Abstract – The paper is devoted to the environmental diamonds and hydrocarbon crude are located in western and impact of industrial sector in Western Yakutia and the south-western parts of the republic. The largest diamond, oil role of the Mirny Polytechnic Institute (branch) of the and gas fields are situated in Western Yakutia. Ammosov North-Eastern Federal University in training specialists for oil and gas and diamond mining industries II. INDUSTRIAL SECTORS OF THE REGION and the research carried out at the educational and scientific laboratory of complex analysis of The area of disturbed lands in Mirny district ranks second anthropogenic disturbances of the Institute on in the Republic after the Neryungrinsky district (about 9 compliance with the requirements. thousand hectares). Key words – environment, industry, oil and gas, diamond The history of diamond mining in Yakutia dates back to mining, ecological monitoring, East Siberia. 1954, when prospectors discovered the first diamond pipe, Zarnitsa (‘Summer Lightning’). In 1957 the Soviet I. INTRODUCTION government established Yakutalmaz Group of enterprises, and diamond mining operations commenced. Two years later The Mirny Polytechnic Institute (branch) of the the USSR sold the first parcel of Yakutian diamonds on the Ammosov North-Eastern Federal University is located in the world market.
    [Show full text]
  • V. Makarov A. Guseynov A. Grigoryev
    ss1-2012:Ss4-2009.qxd 06.02.2012 17:20 Страница 252 E D I T O R I A L C O U N C I L V. MAKAROV A. GUSEYNOV Chairman Editor-in-Chief Academician of RAS Academician of RAS A. GRIGORYEV Deputy Editor-in-Chief M E M B E R S O F T H E C O U N C I L L. ABALKIN, Academician V. STEPIN, Academician A. DEREVYANKO, Academician V. TISHKOV, Academician T. ZASLAVSKAYA, Academician Zh. TOSHCHENKO, Corr. Mem., RAS V. LEKTORSKY, Academician A. DMITRIYEV, Corr. Mem., RAS A. NEKIPELOV, Academician I. BORISOVA, Executive Secretary G. OSIPOV, Academician Managing Editor: Oleg Levin; Production Manager: Len Hoffman SOCIAL SCIENCES (ISSN 0134-5486) is a quarterly publication of the Russian Academy of Sciences (RAS). The articles selected by the Editorial Council are chosen from books and journals originally prepared in the Russian language by authors from 30 institutes of the Russian Academy of Sciences. Statements of fact and opinion appearing in the journal are made on the responsibility of the authors alone and do not imply the endorsement of the Editorial Council. Reprint permission: Editorial Council. Address: 26, Maronovsky pereulok, Moscow, 119991 GSP-1, Russia. SOCIAL SCIENCES (ISSN 0134-5486) is published quarterly by East View Information Services: 10601 Wayzata Blvd., Minneapolis, MN 55305, USA. Vol. 43, No. 1, 2012. Postmaster: Send address changes to East View Information Services: 10601 Wayzata Blvd., Minneapolis, MN 55305, USA. Orders are accepted by East View Information Services. Phone: (952) 252-1201; Toll-free: (800) 477-1005; Fax: (952) 252-1201; E-mail: [email protected] as well as by all major subscription agencies.
    [Show full text]
  • 11-2016-1.Pdf
    Teoretičeskaâ i prikladnaâ nauka Theoretical & Applied Science 11 (43) 2016 International Scientific Journal Theoretical & Applied Science Editor-in Chief: Hirsch index: Alexandr Shevtsov (KZ) h Index RISC = 1 (60) The Editorial Board: Prof. Vladimir Kestelman (USA) h Index Scopus = 2 (30) Prof. Arne Jönsson (Sweden) h Index Scopus = 3 (18) Prof. Sagat Zhunisbekov (KZ) Founder : International Academy of Theoretical & Applied Sciences Published since 2013 year. Issued Monthly. International scientific journal «Theoretical & Applied Science», registered in France, and indexed more than 45 international scientific bases. Address of editorial offices: Djambyl street 128, 080000, Taraz, KZ. Phone: +777727-606-81 E-mail: [email protected] http://T-Science.org Impact Factor ICV = 6.630 ISSN 2308-4944 Impact Factor ISI = 0.829 1 1 based on International Citation Report (ICR) © Сollective of Authors 9 772308 494164 © «Theoretical & Applied Science» International Scientific Journal Theoretical & Applied Science Materials of the International Scientific Practical Conference Education and Innovation November 30, 2016 Scranton, USA The scientific Journal is published monthly 30 number, according to the results of scientific and practical conferences held in different countries and cities. Each conference, the scientific journal, with articles in the shortest time (for 1 day) is placed on the Internet site: http://T-Science.org Each participant of the scientific conference will receive your own copy of a scientific journal to published reports, as well as the certificate of the participant of conference The information in the journal can be used by scientists, graduate students and students in research, teaching and practical work. International Academy expresses gratitude for assistance in development of international connections and formation of journal: Taraz Technical Institute, 080012, Kazakhstan, Taraz, Suleimenov 6, Phone 8 (7262) 45-42-99.
    [Show full text]
  • Final Report (Years 1-5) July 2007
    Darwin Initiative: Project: 162 / 11 / 025 Cross-border conservation strategies for Altai Mountain endemics (Russia, Mongolia, Kazakhstan) Final Report (Years 1-5) July 2007 CONTENTS: DARWIN PROJECT INFORMATION 3 1 PROJECT BACKGROUND/RATIONALE 3 2 PROJECT SUMMARY 4 3 SCIENTIFIC, TRAINING, AND TECHNICAL ASSESSMENT 8 3.1 RESEARCH 8 Methodology 8 Liaison with local authorities and Regional Ecological Committees 9 Data storage and analysis 10 Results 11 3.2 TRAINING AND CAPACITY BUILDING ACTIVITIES. 14 4 PROJECT IMPACTS 15 5 PROJECT OUTPUTS 18 6 PROJECT EXPENDITURE 19 7 PROJECT OPERATION AND PARTNERSHIPS 19 8 ACTIONS TAKEN IN RESPONSE TO ANNUAL REPORT REVIEWS (IF APPLICABLE) 22 9 DARWIN IDENTITY 23 Project 162 / 11 / 025: Altai Mountains. Final Report, August 2007 1 10 LEVERAGE 23 11 SUSTAINABILITY AND LEGACY 24 12 VALUE FOR MONEY 25 APPENDIX I: PROJECT CONTRIBUTION TO ARTICLES UNDER THE CONVENTION ON BIOLOGICAL DIVERSITY (CBD) 27 APPENDIX II: OUTPUTS 29 APPENDIX III: PUBLICATIONS 35 APPENDIX IV: DARWIN CONTACTS 42 APPENDIX V: LOGICAL FRAMEWORK 44 APPENDIX VI: SELECTED TABLES 45 APPENDIX VII: COPIES OF INFORMATION LEAFLETS 52 APPENDIX VIII: PUBLICATIONS WITH SUMMARIES IN ENGLISH 53 APPENDIX IX: COPIES OF OUTPUTS SUPPLIED AS PDF 68 Project 162 / 11 / 025: Altai Mountains. Final Report, August 2007 2 Darwin Initiative for the Survival of Species Final Report Darwin Project Information Project Reference No. 162 / 11 / 025 Project Title Cross-border conservation strategies for Altai Mountain Endemics (Russia, Mongolia, Kazakhstan) Country(ies) UK, Russia, Mongolia, Kazakhstan UK Contractor University of Sheffield Partner Organisation (s) Tomsk State University (Russia); Hovd branch of Mongolian State University; Altai Botanical Gardens (Leninogorsk, Kazakhstan) Darwin Grant Value £184,316.84 Start/End dates 01.04.2002 – 31.03.2007 Reporting period and report 01.04.2005 – 31.03.2007 (Final report) number Project website http://www.ecos.tsu.ru/altai* Author(s), date Dr.
    [Show full text]
  • Chapter 4 Phytogeography of Northeast Asia
    Chapter 4 Phytogeography of Northeast Asia Hong QIAN 1, Pavel KRESTOV 2, Pei-Yun FU 3, Qing-Li WANG 3, Jong-Suk SONG 4 and Christine CHOURMOUZIS 5 1 Research and Collections Center, Illinois State Museum, 1011 East Ash Street, Springfield, IL 62703, USA, e-mail: [email protected]; 2 Institute of Biology and Soil Science, Russian Academy of Sciences, Vladivostok, 690022, Russia, e-mail: [email protected]; 3 Institute of Applied Ecology, Chinese Academy of Sciences, P.O. Box 417, Shenyang 110015, China; 4 Department of Biological Science, College of Natural Sciences, Andong National University, Andong 760-749, Korea, e-mail: [email protected]; 5 Department of Forest Sciences, University of British Columbia, 3041-2424 mail Mall, Vancouver, B.C., V6T 1Z4, Canada, e-mail: [email protected] Abstract: Northeast Asia as defined in this study includes the Russian Far East, Northeast China, the northern part of the Korean Peninsula, and Hokkaido Island (Japan). We determined the species richness of Northeast Asia at various spatial scales, analyzed the floristic relationships among geographic regions within Northeast Asia, and compared the flora of Northeast Asia with surrounding floras. The flora of Northeast Asia consists of 971 genera and 4953 species of native vascular plants. Based on their worldwide distributions, the 971 gen- era were grouped into fourteen phytogeographic elements. Over 900 species of vascular plants are endemic to Northeast Asia. Northeast Asia shares 39% of its species with eastern Siberia-Mongolia, 24% with Europe, 16.2% with western North America, and 12.4% with eastern North America.
    [Show full text]
  • Yakutia) “…The Republic of Sakha (Yakutia) Is the Largest Region in the Russian Federation and One of the Richest in Natural Resources
    Investor's Guide to the Republic of Sakha (Yakutia) “…The Republic of Sakha (Yakutia) is the largest region in the Russian Federation and one of the richest in natural resources. Needless to say, the stable and dynamic development of Yakutia is of key importance to both the Far Eastern Federal District and all of Russia…” President of the Russian Federation Vladimir Putin “One of the fundamental priorities of the Government of the Republic of Sakha (Yakutia) is to develop comfortable conditions for business and investment activities to ensure dynamic economic growth” Head of the Republic of Sakha (Yakutia) Egor Borisov 2 Contents Welcome from Egor Borisov, Head of the Republic of Sakha (Yakutia) 5 Overview of the Republic of Sakha (Yakutia) 6 Interesting facts about the Republic of Sakha (Yakutia) 7 Strategic priorities of the Republic of Sakha (Yakutia) investment policy 8 Seven reasons to start a business in the Republic of Sakha (Yakutia) 10 1. Rich reserves of natural resources 10 2. Significant business development potential for the extraction and processing of mineral and fossil resources 12 3. Unique geographical location 15 4. Stable credit rating 16 5. Convenient conditions for investment activity 18 6. Developed infrastructure for the support of small and medium-sized enterprises 19 7. High level of social and economic development 20 Investment infrastructure 22 Interaction with large businesses 24 Interaction with small and medium-sized enterprises 25 Other organisations and institutions 26 Practical information on doing business in the Republic of Sakha (Yakutia) 27 Public-Private Partnership 29 Information for small and medium-sized enterprises 31 Appendix 1.
    [Show full text]
  • 56 / 2014 — the Dog, the Horse and the Creation Of
    The Dog, the Horse and the Creation of Man «The Dog, the Horse and the Creation of Man» by Yuri Berezkin Source: Folklore: Electronic Journal of Folklore (Folklore: Electronic Journal of Folklore), issue: 56 / 2014, pages: 25­46, on www.ceeol.com. The following ad supports maintaining our C.E.E.O.L. service doi: 10.7592/FEJF2014.56.berezkin THE DOG, THE HORSE AND THE CREATION OF MAN Yuri Berezkin Abstract: A story that described the creation of man became known to at least some inhabitants of the Eurasian Steppe zone not later than the early II millennia B.C. Not a fragment of it survived across most of this area, and our reconstruc- tion is based on the evidence from the areas to the north and to the south of the Steppe Belt. The texts in question share many specific details and the probability of their independent emergence looks negligible. At the same time the people to whom the story was familiar in the 19th and 20th century could definitely not have borrowed it from each other in recent times. The only way to reconstruct the mythology of the people who lived in the past is a search of its survivals in the later folklore. The analysis of ancient iconography or scraps of evidence preserved in the early written sources is not enough for the reconstruction of the plots of complex tales. Keywords: creation myth, creation of man A story that described the creation of man became known to at least some in- habitants of the Eurasian Steppe zone not later than the early II millennia B.C.
    [Show full text]
  • Subject of the Russian Federation)
    How to use the Atlas The Atlas has two map sections The Main Section shows the location of Russia’s intact forest landscapes. The Thematic Section shows their tree species composition in two different ways. The legend is placed at the beginning of each set of maps. If you are looking for an area near a town or village Go to the Index on page 153 and find the alphabetical list of settlements by English name. The Cyrillic name is also given along with the map page number and coordinates (latitude and longitude) where it can be found. Capitals of regions and districts (raiony) are listed along with many other settlements, but only in the vicinity of intact forest landscapes. The reader should not expect to see a city like Moscow listed. Villages that are insufficiently known or very small are not listed and appear on the map only as nameless dots. If you are looking for an administrative region Go to the Index on page 185 and find the list of administrative regions. The numbers refer to the map on the inside back cover. Having found the region on this map, the reader will know which index map to use to search further. If you are looking for the big picture Go to the overview map on page 35. This map shows all of Russia’s Intact Forest Landscapes, along with the borders and Roman numerals of the five index maps. If you are looking for a certain part of Russia Find the appropriate index map. These show the borders of the detailed maps for different parts of the country.
    [Show full text]