Parameter Sensitivity of the Dynamic Roll Over Threshold
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Safety Implications of Various Truck Configurations
SAFETY IMPLICATIONS OF VARIOUS TRUCK CONFIGURATIONS VOLUME 111 SUMMARY REPORT Paul S. Fancher Arvind Mathew January 1989 Technical Report Documentation Page 1. Report No. 2. Government Actereion No. 3. Recipient'r Catalog No. FHWA-RD-89-085 4. Tit* and SubtiUc 5. Report Dete SAFETY IMPLICATIONS OF VARIOUS TRUCK January 1989 CONFIGURATIONS - Vol. 111 6. Performing Organization Code 8, Performing Organlzation Report No. 7. Author(*) Paul S. Fancher, Arvind Mathew UMTRI-88-42 9. Performing Organization Nam and Addnr 10. Work Unit No. (TRAIS) The University of Michigan 11. Contract or Grant No. Transportation Research Institute DTFH61-85-C-00091 2901 Baxter Road, Ann Arbor, Michigan 48 109 13. Typ of Report and Period Covmd 12 Sponroring Agency Name and Addnu Summary Report Office of Safety and Traffic Operations R&D 8-8511-89 Federal Highway Administration 6300 Georgetown Pike, McLean, Virginia 22101-2296 14. Sponroring Agency Code 15. Supplementary Notee FHWA Contract Manager (COTR) - Justin True Subcontractor: Texas Transportation Institute (Dan Middleton) 16. Abrtrlct The purpose of this study is to examine changes to size and weight limits in order to determine their effects on the designs and configurations of heavy vehicles, the performance capabilities of the resulting vehicles, and the ensuing safety implications thereof, The summary report provides results and findings fiom an analytical investigation of the influences of size and weight limits on trucks. In an analytical sense, pavement loading rules and bridge formulas are the inputs to the analyses and vehicle performances are the outputs. Ultimately, the work shows the manner in which size and weight rules influence the safety-related performance of vehicles designed to increase productivity. -

Release Date 6/29/18 This Page Is Intentionally Left Blank
Release Date 6/29/18 This page is intentionally left blank. BODY BUILDER MANUAL CONTENTS SECTION 1: INTRODUCTION SECTION 2: SAFETY AND COMPLIANCE SAFETY SIGNALS 2-1 FEDERAL MOTOR VEHICLE SAFETY STANDARDS AND COMPLIANCE 2-2 NOISE AND EMISSIONS REQUIREMENTS 2-3 FUEL SYSTEM 2-4 COMPRESSED AIR SYSTEM 2-5 EXHAUST AND EXHAUST AFTER-TREATMENT SYSTEM 2-5 COOLING SYSTEM 2-6 ELECTRICAL SYSTEMS 2-7 AIR INTAKE SYSTEM 2-9 CHARGE AIR COOLER SYSTEM 2-9 SECTION 3: DIMENSIONS INTRODUCTION 3-1 ABBREVIATIONS 3-1 OVERALL DIMENSIONS 3-1 SLEEPERS 3-8 FRAME RAILS 3-9 FRAME HEIGHT CHARTS 3-10 REAR FRAME HEIGHTS "C" 3-13 REAR SUSPENSION LAYOUTS 3-16 LIFT AXLES (PUSHERS AND TAGS) 3-28 AXLE TRACK AND TIRE WIDTH 3-31 FRONT DRIVE AXLE, PTO’S AND AUXILIARY TRANSMISSIONS 3-33 EXHAUST HEIGHT CALCULATIONS 3-40 GROUND CLEARANCE CALCULATIONS 3-41 OVERALL CAB HEIGHT CALCULATIONS 3-42 FRAME COMPONENTS 3-43 FRAME SPACE REQUIREMENTS 3-45 567/579 FAMILY 2017 EMISSIONS 3-51 SECTION 4: BODY MOUNTING INTRODUCTION 4-1 FRAME RAILS 4-1 CRITICAL CLEARANCES 4-2 BODY MOUNTING USING BRACKETS 4-3 BODY MOUNTING USING U–BOLTS 4-7 SECTION 5: FRAME MODIFICATIONS INTRODUCTION 5-1 DRILLING RAILS 5-1 MODIFYING FRAME LENGTH 5-1 CHANGING WHEELBASE 5-1 CROSSMEMBERS 5-2 TORQUE REQUIREMENTS 5-3 WELDING 5-3 SECTION 6: CONTROLLER AREA NETWORK (CAN) COMMUNICATIONS INTRODUCTION 6-1 SAE J1939 6-2 PARAMETER GROUP NUMBER 6-2 SUSPECT PARAMETER NUMBER 6-2 CAN MESSAGES AVAILABLE ON BODY CONNECTIONS 6-3 TABLE OF CONTENTS SECTION 7: ELECTRICAL INTRODUCTION 7-1 ELECTRICAL ACRONYM LIBRARY 7-1 ELECTRICAL WIRING -

L761 Rev J 01-20 © 2009 – 2020 Hendrickson USA, L.L.C
UNDERSTANDING TRAILER AIR SUSPENSIONS Trailer Commercial Vehicle Systems A true innovator in the industry, Hendrickson is always on the brink of new and exciting products to adapt to an ever-changing market. With goals of reliability, quality and durability, Hendrickson has proven to be the favored choice in the trailer air suspension market. ULTRAA-K® UTKNT VANTRAAX® HKANT INTRAAX® AAZ HT™ SERIES HT230T INTRAAX® AAL INTRAAX® AANT INTRAAX® AAT RCA CONNEX™-ST CONNEX™ 866-RIDEAIR (743-3247) www.hendrickson-intl.com UNDERSTANDING AIR SUSPENSIONS Table of Contents Overview Air Suspensions ...............................2 Understanding Ride ....................................4 Understanding Roll Stability .............................6 Smart Spec’ing Tips ....................................8 TIREMAAX® .........................................10 User Friendly QUIK-DRAW® .............................12 VANTRAAX® HKANT Controlling Ride Height ...............................14 Loading Dock Solutions ...............................16 Value-Added Features and Options ......................18 Extended-Service Wheel-Ends ...........................20 Brake Efficiency ......................................22 Vehicle Controls .....................................24 Aftermarket .........................................26 Trailer Suspensions ...................................28 Standard Terminology .................................34 Applications. 36 UNDERSTANDING AIR SUSPENSIONS OVERVIEW Air Suspensions The popularity of air suspensions has grown in -

Truck Size and Weight Study Phase I: Working Papers 1 and 2 Combined
Truck Size and Weight Study Phase I: Working Papers 1 and 2 combined Vehicle Characteristics Affecting Safety Paul S. Fancher Kenneth L. Campbell University of Michigan Transportation Research Institute This paper addresses the relationship of truck size and weight (TS&W) policy, vehicle handling and stability, and safety. Handling and stability are the primary mechanisms relating vehicle characteristics and safety. Vehicle characteristics may also affect safety by mechanisms other than handling and stability. For example, vehicle length may affect safety through interactions with other vehicles, such as passing maneuvers and in clearing intersections, in addition to its influence on vehicle handling and stability. However, the safety effect of vehicle length due to its influence on handling and stability is within the scope of this paper, while safety effects arising through mechanisms other than handling and stability, such as passing and intersection clearance, are not. There is no direct relationship between TS&W policy and safety. Vehicle characteristics are altered in response to TS&W policy, and vehicle characteristics also influence handling and stability. A wide variety of vehicle characteristics may satisfy a given TS&W policy, and a wide range of safety effects can result. This paper begins with a discussion of the recent history of TS&W policy, and the influence of past policy on safety. The technical relationships between vehicle characteristics and safety are summarized in Section 2. This material has been condensed from a rather large body of literature. Performance measures are introduced to describe (quantify) the capability of the vehicle in various maneuvers. The material in Section 2 summarizes the relationship of various vehicle characteristics and pertinent performance measures (roll threshold, rearward amplification, braking efficiency, and offtracking). -

Trailer Axle Codes
Trailer Axle Codes Example Axle Part Number — R225S567L715 Below is a breakdown of what our axle part numbers mean: Spindle — ( R225S567L715 ) “R” - Tapered spindle - HM212049/HM218248 bearing combination “P” - Parallel spindle - HM518445/HM518445 bearing combination Wall Thickness — ( R225S567L715 ) “200” - 5/8" Wall rated at 20,000 lbs for air ride, 22,500 lbs for spring suspensions “225” - 5/8" Wall rated at 22,500 lbs for air ride, 25,000 lbs for spring suspensions “250” - 3/4" Wall rated at 25,000 lbs for air ride, 27,500 lbs for spring suspensions Axle Tube — ( R225S567L715 ) “S” - Straight “D” - 6" Drop center Available Axles: Axle Tube Size — ( R225S567L715 ) “R” Series “5” - 5" Round R200D567X715 - 6" Drop center R225S527L715 - 12.25" Brakes Brake Drum Diameter — ( R225S567L715 ) R225S567L715 “6” - 16.5" Drum diameter R225S567L775 “2” - 12.25" Drum diameter R250S527L775 - 12.25" Brakes R250S567L715 Brake Shoe Width — ( R225S567L715 ) R250S567L775 “7” - 7" wide shoe with 16.5" drum “7” - 7.5" wide shoe with 12.25" drum “P” Series P225S567L715 Cam Length — ( R225S567L715 ) P225S567L775 “L” - Straight axle long cam - 24.12" P250S567L715 “X” - Drop center axle - 22.40" P250S567L775 Axle Track — ( R225S567L715 ) “715” - 71.5" axle track “775” - 77.5" axle track (continued on page 2) Trailer Axle Component Options Part Qty/Axle Part Number Description “R” Series - Hub Pilot Wheels 11-0656A-71 Hub Options 2 Short Metric Stud - Steel Wheels 11-0656A-72 Long Metric Stud - Aluminum Wheels Wheel Nuts 20 13-3052 22mm Nut - 33mm Hex “R” Series -

Key Largo Wastewater Treatment District Board of Commissioners Meeting Agenda Item Summary
Key Largo Wastewater Treatment District Board of Commissioners Meeting Agenda Item Summary Meeting Date; Agenda Item Number: H-1 February 16, 2021 Agenda Item Type: Agenda Item Scope: Recommended Action: Information / Presentation Review / Discussion Discussion Department: Sponsor: Finance Maintenance Dept. Subject: Fleet Replacement Plan - Admin Vehicle Summary of Discussion: At the January 5, 2021 KLWTD board meeting. The Board requested that the Admin vehicle purchase portion of the Fleet Replacement plan be placed on the agenda for the Feb. 16, 2021 board meeting. In addition, per Board request, we have included information regarding extended warranty for the Durango, and information regarding the use of employees' personal vehicles. Ea Reviewed I Approved Financial Impact Attachments Operations: 1.Memo 2.Brown & Brown Ins. emails Administration; regarding personal vehicle use Finance: Funding Source: 3.Fleet Replacement Plan for FY21 District Counsel: 4. Vehicle Quote District Clerk: Budgeted: 5. Extended Warranty info Yes 6. Kelley Blue Book info Engineering: El f 2 - //' Approved By: Date: General Manager 12 KLWTD Admin Dept. Vehicle Background: When Ryan Dempsey, Maintenance Manager, brought the fleet replacement plan to the Board, the plan included a replacement vehicle for Admin Dept In FY21, to se ll the Durango on GovDeals. In March 2020, due to Covid-19 policy changes to allow one employee in one vehicle, the Durango was given to Field Dept for use, and has continued to stay with Field Dept. It is no longer available for Admin Dept. use. An Admin Vehicle is used for: Short term Errands: • Monroe County (various offices), DMV, Post Office, KLWTD plant for meetings, records room • Centennial Bank, First St ate Bank • Trips to Marathon and lslamorada for meetings, CPR training; Countywide Meetings Long term trips: • Trips to airport to attend meetings in Tallahassee and Washington DC; Airvac training in Indiana (multiple field employees go at one time, can ta ke Admin vehicle vs. -

L579 DATE: April 2021 REVISION: H
TECHNICAL PROCEDURE TRAILER SUSPENSION SYSTEMS SUBJECT: Alignment Procedures LIT NO: L579 DATE: April 2021 REVISION: H TABLE OF CONTENTS Important Safety Notices ....................................................................................................................... 2 Conventions Applied in This Document ................................................................................................... 2 Explanation of Signal Words ........................................................................................................................ 2 Hyperlinks ................................................................................................................................................... 2 Contacting Hendrickson............................................................................................................................... 2 Relative Literature ....................................................................................................................................... 3 Other relative literature may include: ............................................................................................................ 3 Preparing Trailer for Maintenance Service .................................................................................................... 3 Tools And Equipment ................................................................................................................................... 4 TORX® Sockets ........................................................................................................................................... -

City of Napa Ladder Truck Turn Dimensions
Fire Prevention Division 1600 First Street Napa, CA 94559 Office: (707)-257-9590 Fax: (707) 257-9522 CITY OF NAPA LADDER TRUCK TURN DIMENSIONS Turning Performance Analysis 5/3/2011 Bid Number: 253 Chassis: Velocity Chassis, Aerials, Tandem 48K, PUC (Big Block), 2010 Department: City of Napa Body: Aerial, HD Ladder 105', PUC, Alum Body Parameters: o Inside Cramp Angle: 45 Axle Track: 82.92 in. Wheel Offset: 5.3 in. Tread Width: 17.4 in. Chassis Overhang: 78 in. Additional Bumper Depth: 7 in. Front Overhang: 85 in. Wheelbase: 256.5 in. Calculated Turning Radii: Inside Turn: 20 ft. 2 in. Curb to curb: 36 ft. 7 in. Wall to wall: 40 ft. 11 in. Comments: Note: Truck Length is 42' CategoryID Category Description OptionCode OptionDescription 6 Axle, Front, Custom 0508849 Axle, Front, Oshkosh TAK-4, Non Drive, 22,800 lb, Imp/Vel/Dash CF 30 Wheels, Front 0019618 Wheels, Front, Alcoa, 22.50" x 13.00", Aluminum, Hub Pilot 31 Tires, Front 0594821 Tires, Front, Goodyear, G296 MSA, 425/65R22.50, 20 ply 38 Bumpers 0123628 Bumper, Non-extended, Imp/Vel 437 Aerial Devices 0592925 Aerial, 105' Heavy Duty Ladder Notes: Actual Inside Cramp Angle may be less due to highly specialized options. Curb to Curb turning radius calculated for a 9.00 inch curb. 1 Turning Performance Analysis 5/3/2011 Bid Number: 253 Chassis: Velocity Chassis, Aerials, Tandem 48K, PUC (Big Block), 2010 Department: City of Napa Body: Aerial, HD Ladder 105', PUC, Alum Body Definitions: Inside Cramp Angle Maximum turning angle of the front inside tire. -
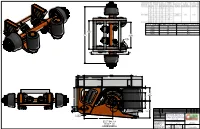
FORWARD<< AA AXLE TRACK BEAM
AXLE TRACK BEAM CENTERS AIR SPRING CENTERS 77.5 39 35 83.5 45 41 BEAM CENTERS 89.5 51 47 AIR 95.5 57 53 AXLE SPRING TRACK CENTERS 1/4 NPT AIR PORT TYP 60 A A 4.29 32.00 .5 MAX (45) (16.56) "D" (9.00) RH SHOWN "UP" E "DOWN" 3 (11.63) B.1 ADDED 45"/51"/57" BEAM CENTER OPTIONS 3/26/19 DJW B UPDATED TO COLOR 3 SHEET DRAWING, AND BOM 11/28/17 DJW 12.7 MAX A UPDATED BOM AND PARTS EXPLOSION 9/11/17 DJW (1.5) DCN# REV REVISION DESCRIPTION DATE BY CHK APP .21 1/4 DRAFTSMAN: DWALKER 11/28/2017 TITLE: CHECKED: CHK CUSH AUXILIARY TRAILER LIFT AXLE ALIGNMENT WELD-ON FOR LOWBOY TRAILER EACH SIDE RELEASED: APP HANGER LIFT SPRING W/ CUSHMATE WEIGHT: N/A 10.4" TOTAL TRAVEL,7.5" TO 10.5" RH, "F" MATERIAL: 9" RH SHOWN All of the Information shown TOLERANCE UNLESS OTHERWISE STATED: SECTION A-A herein is the intellectual property of Cush Corp and is .XX = +/- .062 FRACTIONS = +/- 1/16 Nixa, MO. USA .XXX = +/- .031 ANGLES = +/- 1 PHONE: 417-724-1239 submitted only on a www.cushcorp.com SCALE 1/4 confidential basis. The recipient agrees that no PROJECT NO: SHEET: SCALE: REV: DRAWING(PART) NO: disclosure of this information 1 A-SIZE: NTS <<FORWARD<< will be made to a third party OF without written consent of 17104 B-SIZE: 1/X B.1 CXTL25-W09-x Cush Corp. 3 D-SIZE: 1/8 6 3b 5 1d 3d 1cc 1b 1ca 1d 1cb 1a 3c 2 4 B.1 ADDED 45"/51"/57" BEAM CENTER OPTIONS 3/26/19 DJW B UPDATED TO COLOR 3 SHEET DRAWING, AND BOM 11/28/17 DJW A UPDATED BOM AND PARTS EXPLOSION 9/11/17 DJW DCN# REV REVISION DESCRIPTION DATE BY CHK APP DRAFTSMAN: DWALKER 11/28/2017 TITLE: CHECKED: CHK CUSH AUXILIARY TRAILER LIFT AXLE WELD-ON FOR LOWBOY TRAILER RELEASED: APP HANGER LIFT SPRING W/ CUSHMATE WEIGHT: N/A 10.4" TOTAL TRAVEL,7.5" TO 10.5" RH, MATERIAL: 9" RH SHOWN All of the Information shown TOLERANCE UNLESS OTHERWISE STATED: herein is the intellectual property of Cush Corp and is .XX = +/- .062 FRACTIONS = +/- 1/16 Nixa, MO. -

BODY BUILDER INSTRUCTIONS Mack Trucks
BODY BUILDER INSTRUCTIONS Mack Trucks Body Builder General Information / Specifications CHU, CXU, GU, TD, MRU, LR Section 0 Introduction The information in this document was developed to assist our customers throughout the body planning and installation process. This information will assist with the required specifications and guidelines for completion for your specific applications. The information in this document does not include each and every unique situation that you may encounter when working on Mack vehicles. Mack Trucks cannot possibly know, evaluate, or advise someone on all the types of work that can be done on a Mack vehicle and all the appropriate ways to do such work. This includes all of the possible consequences of performing such work in a certain manner. Therefore, any situations or methods of working on a Mack vehicle that are not addressed in this document are not necessarily approved by Mack. In the event that you require additional assistance, please contact Mack Body Builder Support at 877-770-7575. Unless otherwise stated, following the recommendations listed in this document does not automatically guarantee compliance with applicable government regulations. Compliance with applicable government regulations is your responsibility as the party making the additions/modifications. Please be advised that the Mack Trucks vehicle warranty does not apply to any Mack vehicle that has been modified in any way, which in Mack’s judgment might affect the vehicles stability or reliability. The information, specifications, and illustrations in this document are based on information that was current at the time of publication. Please note that illustrations are typical and may not reflect the exact arrangement of every component installed on a specific vehicle. -
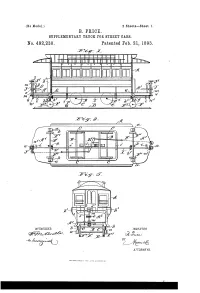
Trinitin,A This
(No Model.) 2. Sheets-Sheet 1. m B. PRICE, SUPPLEMENTARY TRUCK FOR STREET CARS. No. 492,230, Patented Feb. 21, 1893. Z 22 Z, N. FFFFFFFF 4 P 1. - Trinitin,A This al-a’ ;I, a 7 7 he is Il-7Ea WITNESSES A. fWVENTOR (222-2-262. ' 8%. , / %ces.--O SS 2 (6 AITORNEYS. (No Model.) - 2 sheets-Sheet 2. B. PRICE, SUPPLEMENTARY TRUCK FOR STREET CARS, No. 492,230, Patented Feb. 21, 1893. NVNSYN N - - - -- az al SS - SR2 EEsayase SS ES ES5Geziry-A fi 2 WITNESSES ATTORNEYS. he NORRIS Peters co. Phof)-titc. washington, d. c. UNITED STATES PATENT OFFICE. BENNETT PRICE, OF BROOKLYN, NEW YORK. SUPPLEMENTARY TRUCK FOR STREET CARS. SPECIFICATION forming part of Letters Patent No. 492,230, dated February 21, 1893. Application filed October 24, 1892, Serial No. 449,841, (No model.) To all whom it may concern. forms A, are projected, to furnish means for Be it known that I, BENNETT PRICE, of entering the car, and for the accommodation Brooklyn, in the county of Kings and State of of the driver or motor man, common brake New York, have invented new and useful Im rigging E, being furnished for the control of 55 provements in Supplementary Trucks for the vehicle when it is to be stopped. Street-Railway Cars, of which the following is The improvement consists essentially, in a full, clear, and exact description. the provision of two supplementary trucks, Railway lines occupying streets of a town one for each end of the car, each truck com or city, are at times blocked by the stretch prising a single transverse axle, having a pair O ing of lines of hose across their tracks during of wheels, and attachments therefor, that by a fire, or from the disablement of a car due manipulation from the car platforms, will ele to a broken wheel or axle on it. -

Analytic Determination and Numerical Simulation of Torsional Stiffness of a Racing Car Frame
28TH DAAAM INTERNATIONAL SYMPOSIUM ON INTELLIGENT MANUFACTURING AND AUTOMATION DOI: 10.2507/28th.daaam.proceedings.094 ANALYTIC DETERMINATION AND NUMERICAL SIMULATION OF TORSIONAL STIFFNESS OF A RACING CAR FRAME Michal Skovajsa, Frantisek Sedlacek This Publication has to be referred as: Skovajsa, M[ichal] & Sedlacek, F[rantisek] (2017). Analytic Determination and Numerical Simulation of Torsional Stiffness of a Racing Car Frame, Proceedings of the 28th DAAAM International Symposium, pp.0671-0678, B. Katalinic (Ed.), Published by DAAAM International, ISBN 978-3-902734-11-2, ISSN 1726-9679, Vienna, Austria DOI: 10.2507/28th.daaam.proceedings.094 Abstract The paper deals with the determination of the required torsional stiffness of the frame of a racing car. The required torsional stiffness of the frame was performed by analytic computation. The analytic computation deals with the transfer of the vertical load of the tyre between the front and rear axle for different roll stiffnesses of axles and torsional stiffnesses of the frame. The analytic computation determines the ratio between the roll stiffness of the axles and the torsional stiffness of frame. NX Nastran 11 software was used for the numerical simulation. The numerical simulation was performed by using four different numerical methods. Each numerical simulation was performed with different boundary conditions. Keywords: Torsional stiffness; frame; numerical simulation; analytic solution 1. Introduction Determining the correct ratio between the roll stiffness of the car and the torsion stiffness of the frame is covered by several publications. [1, 2, 3]. The numerical simulation of the torsion stiffness of the frame is covered by some publications [5,6].