DOCSLIB.ORG

A Kinetic Model for G Protein-Coupled Signal Transduction in Macrophage Cells

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Kinetic Model for G Protein-Coupled Signal Transduction in Macrophage Cells A Kinetic Model for G protein-coupled Signal Transduction in Macrophage Cells Patrick Joseph Flaherty Electrical Engineering and Computer Sciences University of California at Berkeley Technical Report No. UCB/EECS-2007-4 http://www.eecs.berkeley.edu/Pubs/TechRpts/2007/EECS-2007-4.html January 6, 2007 Copyright © 2007, by the author(s). All rights reserved. Permission to make digital or hard copies of all or part of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. To copy otherwise, to republish, to post on servers or to redistribute to lists, requires prior specific permission. A Kinetic Model for G protein-coupled Signal Transduction in Macrophage Cells by Patrick Joseph Flaherty B.S. (Rochester Institute of Technology) 2000 M.S. (University of California at Berkeley) 2003 A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Engineering-Electrical Engineering and Computer Sciences and the Designated Emphasis in Communication, Computation, and Statistics and Computational Biology in the GRADUATE DIVISION of the UNIVERSITY OF CALIFORNIA, BERKELEY Committee in charge: Professor Michael I. Jordan, Chair Professor Adam P. Arkin Professor Richard M. Karp Fall 2006 The dissertation of Patrick Joseph Flaherty is approved: Chair Date Date Date University of California, Berkeley Fall 2006 A Kinetic Model for G protein-coupled Signal Transduction in Macrophage Cells Copyright 2006 by Patrick Joseph Flaherty 1 Abstract A Kinetic Model for G protein-coupled Signal Transduction in Macrophage Cells by Patrick Joseph Flaherty Doctor of Philosophy in Engineering-Electrical Engineering and Computer Sciences and the Designated Emphasis in Communication, Computation, and Statistics and Computational Biology University of California, Berkeley Professor Michael I. Jordan, Chair Macrophage cells that are stimulated by two different ligands which bind to G protein- coupled receptors (GPCRs) usually respond as if the stimulus effects are additive, but for a minority of ligand combinations the response is synergistic. The G protein-coupled receptor system integrates multiple, perhaps conflicting, signaling cues from the environment in order to actuate cell morphology, gene expression, ion homeostasis and other physiological states. We study, in detail, the effects of the two signaling molecules complement factor 5a (C5a) and uridine diphosphate (UDP) on the intracellular second messenger calcium to elucidate 2 principals that govern the mechanism of G protein-coupled signal transduction. We have developed a formal hypothesis, in the form of a kinetic model, for the mechanism of action of this GPCR signal transduction system using data obtained from RAW264.7 macrophage cells. Bayesian statistical methods are employed to formally approach uncertainty and tie the model to experimental data. The model is entertained as a tool in the design of investigative experiments. The model accurately predicts a synergistic region in the calcium peak height dose response that results when cells are simultaneous stimulated by C5a and UDP. Though this model is not a complete representation of the G protein-coupled signal transduction system and contains many approximations, it is consistent with our experimental observations and is a useful substrate for further experimentation. Finally, we address the problem of the design of robust experiments for the G protein-coupled signal transduction model. Classical optimal experiment design methods have not been widely adopted in practice for biological systems, in part because the resulting designs can be very brittle if the nominal parameter estimates for the model are poor, and in part because of computational constraints. We present a method for robust experiment design based on a semidefinite programming relaxation. We present an application of this method to the design of experiments for a complex calcium signal transduction pathway, where we have found that the parameter estimates obtained from the robust design are better than those obtained from an “optimal” design. Professor Michael I. Jordan Dissertation Committee Chair i To my family. ii Acknowledgments Many people have volunteered their aid through my work on projects in graduate school and deserve recognition for their selfless help. Though research involving a combination of statistics, engineering and biology is now common, my advisors Michael Jordan and Adam Arkin took a great risk years ago to mentor such research and should be recognized. They have guided, tutored, questioned, challenged and cheered me throughout my time in graduate school and their direction has helped me find my own place in the academic world. The students in the Jordan group were a constant source of learning. I have Alice Zheng to thank for telling me about the Jordan group and encouraging me to attend the group meetings. Dave Blei spent hours teaching me the details of his research so that I would be able to use it for my own. Guri Giaever believed in me and used my research before I might have even used it myself. Guri’s faith helped me to believe that my work can be useful and must meet the highest standards. My work with the Alliance for Cellular Signaling began with a short meeting with Mel Simon. Even since I have looked to Mel for guidance and advise in all of my work. He’s the most insightful, idealistic and kind scientist I have known. I first joined the Arkin lab after meeting with Denise Wolf and thank her for her inspiration and infectious, but playful thirst for knowledge. Tim Ham and Robin Osterhout were there even after hours of studying for prelim exams in room 214. Matt Onsum intro- duced me to the project of this thesis and deserves much of the credit for making the first, but most important steps that I followed. Leor Weinberger taught many of us in the Arkin lab the real meaning of doing good science and that success comes only after hard work. iii Even as an undergraduate student Richie Koche showed his potential as a great scientist. He knew when to work late and when to drag me out of lab for a break after a full day. I first met Shilpa Shroff in the Arkin Lab when I needed a place to live. Shilpa offered her apartment and years later I’ve found a best friend. Finally and most importantly, my family has always supported me with phone calls, cookies, trips home to the farm and constant reminders of the truly important things in life. iv Contents List of Figures vi List of Tables viii 1 Introduction 1 2 G protein-coupled Receptor Signal Transduction Model 6 2.1 ModelStructure ................................. 9 2.1.1 Background................................ 10 2.1.2 Overview ................................. 12 2.2 ReceptorReactions............................... 14 2.2.1 P2YReceptor............................... 15 2.2.2 C5aReceptor............................... 16 2.3 GProteinReactions ............................... 16 2.3.1 Gαi Activation .............................. 18 2.3.2 Gαq Activation.............................. 19 2.4 Phosphoinositide Cascade Reactions . ...... 19 2.4.1 IP3 synthesis by Gαq activated PLCβ3 ................ 23 2.4.2 IP3 synthesis by Gβγ activated PLCβ3 ................ 24 2.4.3 IP3 synthesis by Gαq activated PLCβ4 ................ 25 2.5 IP3ReceptorReactions . .. .. .. .. .. .. .. .. 26 2.5.1 ATPase Pumps and Na2+/Ca2+ Exchangers.. .. .. .. 30 2.5.2 CalciumBuffers ............................. 32 2.6 FeedbackReactions............................... 34 2.6.1 ProteinKinaseC............................. 35 2.6.2 Calcium and DAG are required for PKC activation . 36 2.6.3 GproteinReceptorKinase . 38 2.6.4 Gβγ and PKC are required for GRK activation . 40 2.6.5 RGS is a GAP for Gαq-GTP and Gαi-GTP.............. 41 2.7 Dephosphorylation and Degradation Reactions . ........ 41 2.7.1 C5aR and PLCβ3/4dephosphorylation . 42 2.7.2 DAG degradation and PIP2 synthesis . 42 CONTENTS v 3 Model and Data Analysis 44 3.1 ExperimentalProtocol . 45 3.2 SimulationMethod................................ 46 3.3 InputModel.................................... 46 3.4 Wild-typeData.................................. 48 3.5 KnockdownData................................. 49 3.5.1 GRK2Knockdown ............................ 50 3.5.2 Gαi Knockdown ............................. 51 3.5.3 Gαq Knockdown ............................. 52 3.5.4 PLCβ3Knockdown ........................... 52 3.5.5 PLCβ4Knockdown ........................... 53 3.6 Toxins....................................... 53 3.7 Synergistic Interaction between C5a and UDP . ....... 56 3.7.1 CrosstalkMechanism........................... 59 4 Statistical Inference 62 4.1 BayesianInference ............................... 63 4.1.1 Parameter Confidence Intervals . 64 4.1.2 Prediction Confidence Intervals . 66 4.2 MarkovChainMonteCarlo . 68 4.2.1 Gauss-HermiteQuadrature . 68 4.2.2 LaplaceApproximation . .. .. .. .. .. .. .. 69 4.2.3 Markov Chain Monte Carlo . 70 4.3 PosteriorDensityAnalysis. 72 5 Experiment Design 76 5.1 Locally Optimal Experiment Design . 79 5.2 RobustExperimentDesign . 80 5.3 Application to G protein-coupled Receptor Model . ......... 83 5.3.1 Michaelis-Menten Reaction Model . 83 5.3.2 Calcium Signal Transduction Model . 85 5.4 Discussion..................................... 88 6 Conclusion 90 A Model Implementation 106 A.1 ModelEquations ................................. 106
Load more

Recommended publications
  • The B Vitamins Nicotinamide (B3) and Riboflavin (B2)
    The B Vitamins Nicotinamide (B3) and Riboflavin (B2) Stimulate Metamorphosis in Larvae of the Deposit- Feeding Polychaete Capitella teleta: Implications for a Sensory Ligand-Gated Ion Channel Robert T. Burns1*, Jan A. Pechenik1, William J. Biggers2, Gia Scavo2, Christopher Lehman2 1 Department of Biology, Tufts University, Medford, Massachusetts, United States of America, 2 Department of Biology, Wilkes University, Wilkes-Barre, Pennsylvania, United States of America Abstract Marine sediments can contain B vitamins, presumably incorporated from settled, decaying phytoplankton and microorganisms associated with decomposition. Because B vitamins may be advantageous for the energetically intensive processes of metamorphosis, post-metamorphic growth, and reproduction, we tested several B vitamins to determine if they would stimulate larvae of the deposit-feeding polychaete Capitella teleta to settle and metamorphose. Nicotinamide and riboflavin individually stimulated larvae of C. teleta to settle and metamorphose, generally within 1–2 hours at nicotinamide concentrations as low as 3 mM and riboflavin concentrations as low as 50 mM. More than 80% of the larvae metamorphosed within 30 minutes at a nicotinamide concentration of 7 mM. The pyridine channel agonist pyrazinecarboxamide also stimulated metamorphosis at very low concentrations. In contrast, neither lumichrome, thiamine HCl, pyridoxine HCl, nor vitamin B12 stimulated larvae of C. teleta to metamorphose at concentrations as high as 500 mM. Larvae also did not metamorphose in response to either nicotinamide or pyrazinecarboxamide in calcium-free seawater or with the addition of 4-acetylpyridine, a competitive inhibitor of the pyridine receptor. Together, these results suggest that larvae of C. teleta are responding to nicotinamide and riboflavin via a chemosensory pyridine receptor similar to that previously reported to be present on crayfish chela and involved with food recognition.
    [Show full text]
  • Neural Stem Cell-Derived Exosomes Revert HFD-Dependent Memory Impairment Via CREB-BDNF Signalling
    International Journal of Molecular Sciences Article Neural Stem Cell-Derived Exosomes Revert HFD-Dependent Memory Impairment via CREB-BDNF Signalling Matteo Spinelli 1, Francesca Natale 1,2, Marco Rinaudo 1, Lucia Leone 1,2, Daniele Mezzogori 1, Salvatore Fusco 1,2,* and Claudio Grassi 1,2 1 Department of Neuroscience, Università Cattolica del Sacro Cuore, 00168 Rome, Italy; [email protected] (M.S.); [email protected] (F.N.); [email protected] (M.R.); [email protected] (L.L.); [email protected] (D.M.); [email protected] (C.G.) 2 Fondazione Policlinico Universitario Agostino Gemelli IRCCS, 00168 Rome, Italy * Correspondence: [email protected] Received: 6 October 2020; Accepted: 25 November 2020; Published: 26 November 2020 Abstract: Overnutrition and metabolic disorders impair cognitive functions through molecular mechanisms still poorly understood. In mice fed with a high fat diet (HFD) we analysed the expression of synaptic plasticity-related genes and the activation of cAMP response element-binding protein (CREB)-brain-derived neurotrophic factor (BDNF)-tropomyosin receptor kinase B (TrkB) signalling. We found that a HFD inhibited both CREB phosphorylation and the expression of a set of CREB target genes in the hippocampus. The intranasal administration of neural stem cell (NSC)-derived exosomes (exo-NSC) epigenetically restored the transcription of Bdnf, nNOS, Sirt1, Egr3, and RelA genes by inducing the recruitment of CREB on their regulatory sequences. Finally, exo-NSC administration rescued both BDNF signalling and memory in HFD mice. Collectively, our findings highlight novel mechanisms underlying HFD-related memory impairment and provide evidence of the potential therapeutic effect of exo-NSC against metabolic disease-related cognitive decline.
    [Show full text]
  • Neurotransmitters-Drugs Andbrain Function.Pdf
    Neurotransmitters, Drugs and Brain Function. Edited by Roy Webster Copyright & 2001 John Wiley & Sons Ltd ISBN: Hardback 0-471-97819-1 Paperback 0-471-98586-4 Electronic 0-470-84657-7 Neurotransmitters, Drugs and Brain Function Neurotransmitters, Drugs and Brain Function. Edited by Roy Webster Copyright & 2001 John Wiley & Sons Ltd ISBN: Hardback 0-471-97819-1 Paperback 0-471-98586-4 Electronic 0-470-84657-7 Neurotransmitters, Drugs and Brain Function Edited by R. A. Webster Department of Pharmacology, University College London, UK JOHN WILEY & SONS, LTD Chichester Á New York Á Weinheim Á Brisbane Á Singapore Á Toronto Neurotransmitters, Drugs and Brain Function. Edited by Roy Webster Copyright & 2001 John Wiley & Sons Ltd ISBN: Hardback 0-471-97819-1 Paperback 0-471-98586-4 Electronic 0-470-84657-7 Copyright # 2001 by John Wiley & Sons Ltd. Bans Lane, Chichester, West Sussex PO19 1UD, UK National 01243 779777 International ++44) 1243 779777 e-mail +for orders and customer service enquiries): [email protected] Visit our Home Page on: http://www.wiley.co.uk or http://www.wiley.com All Rights Reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except under the terms of the Copyright, Designs and Patents Act 1988 or under the terms of a licence issued by the Copyright Licensing Agency Ltd, 90 Tottenham Court Road, London W1P0LP,UK, without the permission in writing of the publisher. Other Wiley Editorial Oces John Wiley & Sons, Inc., 605 Third Avenue, New York, NY 10158-0012, USA WILEY-VCH Verlag GmbH, Pappelallee 3, D-69469 Weinheim, Germany John Wiley & Sons Australia, Ltd.
    [Show full text]
  • Investigation of Candidate Genes and Mechanisms Underlying Obesity
    Prashanth et al. BMC Endocrine Disorders (2021) 21:80 https://doi.org/10.1186/s12902-021-00718-5 RESEARCH ARTICLE Open Access Investigation of candidate genes and mechanisms underlying obesity associated type 2 diabetes mellitus using bioinformatics analysis and screening of small drug molecules G. Prashanth1 , Basavaraj Vastrad2 , Anandkumar Tengli3 , Chanabasayya Vastrad4* and Iranna Kotturshetti5 Abstract Background: Obesity associated type 2 diabetes mellitus is a metabolic disorder ; however, the etiology of obesity associated type 2 diabetes mellitus remains largely unknown. There is an urgent need to further broaden the understanding of the molecular mechanism associated in obesity associated type 2 diabetes mellitus. Methods: To screen the differentially expressed genes (DEGs) that might play essential roles in obesity associated type 2 diabetes mellitus, the publicly available expression profiling by high throughput sequencing data (GSE143319) was downloaded and screened for DEGs. Then, Gene Ontology (GO) and REACTOME pathway enrichment analysis were performed. The protein - protein interaction network, miRNA - target genes regulatory network and TF-target gene regulatory network were constructed and analyzed for identification of hub and target genes. The hub genes were validated by receiver operating characteristic (ROC) curve analysis and RT- PCR analysis. Finally, a molecular docking study was performed on over expressed proteins to predict the target small drug molecules. Results: A total of 820 DEGs were identified between
    [Show full text]
  • Understanding Allergic Multimorbidity Within the Non-Eosinophilic
    University of Groningen Understanding allergic multimorbidity within the non-eosinophilic interactome Aguilar, Daniel; Lemonnier, Nathanael; Koppelman, Gerard H; Melén, Erik; Oliva, Baldo; Pinart, Mariona; Guerra, Stefano; Bousquet, Jean; Anto, Josep M Published in: PLoS ONE DOI: 10.1371/journal.pone.0224448 IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish to cite from it. Please check the document version below. Document Version Publisher's PDF, also known as Version of record Publication date: 2019 Link to publication in University of Groningen/UMCG research database Citation for published version (APA): Aguilar, D., Lemonnier, N., Koppelman, G. H., Melén, E., Oliva, B., Pinart, M., Guerra, S., Bousquet, J., & Anto, J. M. (2019). Understanding allergic multimorbidity within the non-eosinophilic interactome. PLoS ONE, 14(11), [e0224448]. https://doi.org/10.1371/journal.pone.0224448 Copyright Other than for strictly personal use, it is not permitted to download or to forward/distribute the text or part of it without the consent of the author(s) and/or copyright holder(s), unless the work is under an open content license (like Creative Commons). Take-down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Downloaded from the University of Groningen/UMCG research database (Pure): http://www.rug.nl/research/portal. For technical reasons the number of authors shown on this cover page is limited to 10 maximum. Download date: 26-12-2020 RESEARCH ARTICLE Understanding allergic multimorbidity within the non-eosinophilic interactome 1,2,3 4 5,6 7 Daniel AguilarID *, Nathanael LemonnierID , Gerard H.
    [Show full text]
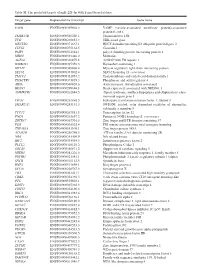
  • Table SI. the Predicted Targets of Mir-221-3P with Targetscan Database
    Table SI. The predicted targets of miR-221-3p with TargetScan database. Target gene Representative transcript Gene name VAPB ENST00000395802.3 VAMP (vesicle-associated membrane protein)-associated protein B and C TMSB15B ENST00000540220.1 Thymosin beta 15B TFG ENST00000240851.4 TRK-fused gene HECTD2 ENST00000371667.1 HECT domain containing E3 ubiquitin protein ligase 2 CLVS2 ENST00000275162.5 Clavesin 2 PAIP1 ENST00000514514.1 poly(A) binding protein interacting protein 1 MIDN ENST00000591446.2 Midnolin AGFG1 ENST00000310078.8 ArfGAP with FG repeats 1 HMBOX1 ENST00000397358.3 Homeobox containing 1 MYLIP ENST00000349606.4 Myosin regulatory light chain interacting protein SEC62 ENST00000337002.4 SEC62 homolog (S. cerevisiae) TMCC1 ENST00000432054.2 Transmembrane and coiled-coil domain family 1 PHACTR4 ENST00000373839.3 Phosphatase and actin regulator 4 AIDA ENST00000340020.6 Axin interactor, dorsalization associated BEAN1 ENST00000299694.8 Brain expressed, associated with NEDD4, 1 AMMECR1 ENST00000262844.5 Alport syndrome, midface hypoplasia and elliptocytosis chro- mosomal region gene 1 EIF3J ENST00000261868.5 Eukaryotic translation initiation factor 3, subunit J SMARCA5 ENST00000283131.3 SWI/SNF related, actin dependent regulator of chromatin, subfamily a, member 5 TCF12 ENST00000267811.5 Transcription factor 12 PNO1 ENST00000263657.2 Partner of NOB1 homolog (S. cerevisiae) ZBTB37 ENST00000367701.5 Zinc finger and BTB domain containing 37 FOS ENST00000303562.4 FBJ murine osteosarcoma viral oncogene homolog ZNF385A ENST00000551109.1 Zinc
    [Show full text]
  • This Thesis Has Been Submitted in Fulfilment of the Requirements for a Postgraduate Degree (E.G
    This thesis has been submitted in fulfilment of the requirements for a postgraduate degree (e.g. PhD, MPhil, DClinPsychol) at the University of Edinburgh. Please note the following terms and conditions of use: This work is protected by copyright and other intellectual property rights, which are retained by the thesis author, unless otherwise stated. A copy can be downloaded for personal non-commercial research or study, without prior permission or charge. This thesis cannot be reproduced or quoted extensively from without first obtaining permission in writing from the author. The content must not be changed in any way or sold commercially in any format or medium without the formal permission of the author. When referring to this work, full bibliographic details including the author, title, awarding institution and date of the thesis must be given. The CX3CR1/CX3CL1 Axis Drives the Migration and Maturation of Oligodendroglia in the Central Nervous System Catriona Ford Thesis Submitted for the Degree of Doctor of Philosophy The University of Edinburgh 2017 Abstract In the central nervous system, the axons of neurons are protected from damage and aided in electrical conductivity by the myelin sheath, a complex of proteins and lipids formed by oligodendrocytes. Loss or damage to the myelin sheath may result in impairment of electrical axonal conduction and eventually to neuronal death. Such demyelination is responsible, at least in part, for the disabling neurodegeneration observed in pathologies such as Multiple Sclerosis (MS) and Spinal Cord Injury. In the regenerative process of remyelination, oligodendrocyte precursor cells (OPCs), the resident glial stem cell population of the adult CNS, migrate toward the injury site, proliferate and differentiate into adult oligodendrocytes which subsequently reform the myelin sheath.
    [Show full text]
  • Supplemental Figures
    Supplemental Figures Supplemental figure legends Figure S1 | Testing the pre-clustering heuristic. (A) (Left) Default, unsupervised heuristic sets a cut of 7% of the total dendrogram depth, which results in 52 pre-clusters. (Right) The numerical model calculated using the 52 pre-clusters. Xc1 and Xc2 represent the expression (in a binned UMIs grid) of a given gene X in two cells c1 and c2 belonging to the same pre-cluster. The cumulative distribution plot estimates the frequency, hence likelihood, of an expression change. (B) (Left) Forcing a cut of only 4% creates 1152 pre-clusters, more than 20-fold increase compared to the default 7% depth. Also, given the reduction of the average cluster size and the consequent reduction of possible intra-cluster pair-wise comparison, the number of data points used to fit the model decreases of more than 5-fold compared to default 7% cut (from 3.79E+9 to 6.56E+8). (Right) Despite this, the difference between the numerical model of 4% cut and 7% cut is marginal. (C) (Left) Forcing a cut of 20% creates only 9 pre-clusters, which is less than the number of final clusters (in this case, 11) and therefore represents a miscalculated configuration. Still the difference between the numerical model of 20% cut and 7% cut is marginal (right). (D) Also switching from Pearson to Spearman correlation is associated with neglectable differences in the numerical model. (E) (Top) Number of pre-clusters associated with the different cutting depths, correlations metrics (Pearson, Spearman) or linkage metrics (complete or Weighted average distance, WPGMA, instead of default Ward’s).
    [Show full text]
  • Identification of Key Pathways and Genes in Dementia Via Integrated Bioinformatics Analysis
    bioRxiv preprint doi: https://doi.org/10.1101/2021.04.18.440371; this version posted July 19, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. Identification of Key Pathways and Genes in Dementia via Integrated Bioinformatics Analysis Basavaraj Vastrad1, Chanabasayya Vastrad*2 1. Department of Biochemistry, Basaveshwar College of Pharmacy, Gadag, Karnataka 582103, India. 2. Biostatistics and Bioinformatics, Chanabasava Nilaya, Bharthinagar, Dharwad 580001, Karnataka, India. * Chanabasayya Vastrad [email protected] Ph: +919480073398 Chanabasava Nilaya, Bharthinagar, Dharwad 580001 , Karanataka, India bioRxiv preprint doi: https://doi.org/10.1101/2021.04.18.440371; this version posted July 19, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. Abstract To provide a better understanding of dementia at the molecular level, this study aimed to identify the genes and key pathways associated with dementia by using integrated bioinformatics analysis. Based on the expression profiling by high throughput sequencing dataset GSE153960 derived from the Gene Expression Omnibus (GEO), the differentially expressed genes (DEGs) between patients with dementia and healthy controls were identified. With DEGs, we performed a series of functional enrichment analyses. Then, a protein–protein interaction (PPI) network, modules, miRNA-hub gene regulatory network and TF-hub gene regulatory network was constructed, analyzed and visualized, with which the hub genes miRNAs and TFs nodes were screened out. Finally, validation of hub genes was performed by using receiver operating characteristic curve (ROC) analysis.
    [Show full text]
  • The Metabotropic Receptor Mglur6 May Signal Through Go, but Not Phosphodiesterase, in Retinal Bipolar Cells
    The Journal of Neuroscience, April 15, 1999, 19(8):2938–2944 The Metabotropic Receptor mGluR6 May Signal Through Go, But Not Phosphodiesterase, in Retinal Bipolar Cells Scott Nawy Departments of Ophthalmology and Visual Science, and Neuroscience, Albert Einstein College of Medicine, Bronx, New York 10461 Bipolar cells are retinal interneurons that receive synaptic input with cells dialyzed with cGMP alone. Comparable results were from photoreceptors. Glutamate, the photoreceptor transmitter, obtained with the PDE inhibitor 3-isobutyl-1-methyl-xanthine hyperpolarizes On bipolar cells by closing nonselective cation (IBMX) or with 8-pCPT-cGMP and IBMX together, indicating channels, an effect mediated by the metabotropic receptor that PDE is not required for mGluR6 signal transduction. Addi- a mGluR6. Previous studies of mGluR6 transduction have sug- tion of the G-protein subunit Go to the pipette solution sup- gested that the receptor couples to a phosphodiesterase (PDE) pressed the cation current and occluded the glutamate re- a bg that preferentially hydrolyzes cGMP, and that cGMP directly gates sponse, whereas dialysis with Gi or with transducin G had the nonselective cation channel. This hypothesis was tested by no significant effect on either the cation current or the response. a dialyzing On bipolar cells with nonhydrolyzable analogs of cGMP. Dialysis of an antibody directed against Go also reduced the Whole-cell recordings were obtained from On bipolar cells in slices glutamate response, indicating a functional role for endoge- a of larval tiger salamander retina. Surprisingly, On bipolar cells nous Go . These results indicate that mGluR6 may signal dialyzed with 8-(4-chlorophenylthio)-cyclic GMP (8-pCPT-cGMP), through Go , rather than a transducin-like G-protein.
    [Show full text]
  • Pharmacology of CNS Introduction: Ion Channels and Neurotransmitters Receptors
    Forth stage: 1st semester Pharmacology II lec:1 Pharmacology of CNS Introduction: Drugs acting in the central nervous system (CNS) were among the first to be discovered by primitive humans and are still the most widely used group of pharmacologic agents. In addition to their use in therapy, many drugs acting on the CNS are used without prescription to increase one's sense of well-being. The mechanisms by which various drugs act in the CNS have not always been clearly understood. However, it is clear that nearly all drugs with CNS effects act on specific receptors that modulate synaptic transmission. A very few agents such as general anesthetics and alcohol may have nonspecific actions on membranes (although these exceptions are not fully accepted), but even these non–receptor-mediated actions result in demonstrable alterations in synaptic transmission. Furthermore, the action of drugs with known clinical efficacy has led to some of the most fruitful hypotheses regarding the mechanisms of disease. For example, information on the action of antipsychotic drugs on dopamine receptors has provided the basis for important hypotheses regarding the pathophysiology schizophrenia. Studies of the effects of a variety of agonists and antagonists on - aminobutyric acid (GABA) receptors has resulted in new concepts pertaining to the pathophysiology of several diseases, including anxiety and epilepsy. In order to understand the pharmacology action of drugs on CNS, it's important to have a review about the functional organization of the CNS, its synaptic transmitters, ion channels and neurotransmitter receptors. Ion channels and neurotransmitters receptors: -The membranes of nerve cells contain two types of channels defined on the basis of the mechanisms controlling their gating (opening and closing): voltage-gated and ligand-gated ion channels.
    [Show full text]
  • The University of Chicago Sk2 Channel and Metabotropic
    THE UNIVERSITY OF CHICAGO SK2 CHANNEL AND METABOTROPIC RECEPTOR MEDIATED REGULATION OF INTRINSIC EXCITABILITY IN PURKINJE CELLS AND IMPLICATIONS FOR CEREBELLAR LEARNING A DISSERTATION SUBMITTED TO THE FACULTY OF THE DIVISION OF THE BIOLOGICAL SCIENCES AND THE PRITZKER SCHOOL OF MEDICINE IN CANDIDACY FOR THE DEGREE OF DOCTOR OF PHILOSOPHY COMMITTEE ON NEUROBIOLOGY BY GABRIELLE WATKINS CHICAGO, ILLINOIS MARCH 2021 Copyright © 2021 by Gabrielle Watkins All Rights Reserved TABLE OF CONTENTS LIST OF FIGURES . iv LIST OF ABBREVIATIONS . v ACKNOWLEDGMENTS . vii TECHNICAL ABSTRACT . viii 1 GENERAL INTRODUCTION AND BACKGROUND . 1 1.1 Learning & Memory . 1 1.2 The Cerebellum . 3 2 MECHANISMS OF EXPRESSION & MODULATION OF INTRINSIC PLASTICITY IN CEREBELLAR PURKINJE CELLS . 6 2.1 Rationale . 6 2.2 Materials & Methods . 6 2.3 Intrinsic plasticity can be induced through physiologically relevant stimuli . 9 2.4 Expression of both synaptic and SD induced intrinsic plasticity in Purkinje cells is dependent on SK2 channels . 13 2.5 Metabotropic receptor activity modulates expression of intrinsic plasticity . 17 2.6 Expression of intrinsic plasticity is mediated by PKA . 23 2.7 Discussion . 25 3 CEREBELLUM-DEPENDENT ASSOCIATIVE LEARNING INDUCES CHANGES IN PURKINJE CELL INTRINSIC EXCITABILITY . 28 3.1 Rationale . 28 3.2 Materials & Methods . 28 3.3 Mice successfully perform a cerebellum-dependent associative learning task . 32 3.4 Spontaneous and evoked spiking activity is not affected by associative learning . 34 3.5 Conditioned animals demonstrate a reduction in AHP . 36 3.6 Intrinsic plasticity expression is occluded in cells from conditioned mice . 40 3.7 Discussion . 42 4 GENERAL DISCUSSION . 44 4.1 Intrinsic and synaptic plasticity are induced under similar conditions .
    [Show full text]