Understanding Chemical Changes Across the Α‑Cristobalite to Stishovite Transition Path in Silica † † ‡ † † Miguel A
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Crystalline Silica, Cristobalite (CAS No
Crystalline Silica, Quartz (CAS No. 14808-60-7) Crystalline Silica, Cristobalite (CAS No. 14464-46-1) Crystalline Silica, Tridymite (CAS No. 15468-32-3) Diatomaceous earth (CAS No. 61790-53-2) This dossier on crystalline silica, quartz, cristobalite and tridymite and diatomaceous earth presents the most critical studies pertinent to the risk assessment of these substances in their use in drilling muds and cement additives. This dossier does not represent an exhaustive or critical review of all available data. The majority of information presented in this dossier was obtained from the ECHA database that provides information on chemicals that have been registered under the EU REACH (ECHA). Where possible, study quality was evaluated using the Klimisch scoring system (Klimisch et al., 1997). For the purpose of this dossier, crystalline silica, quartz (CAS No. 14808-60-7) has been reviewed as representative of crystalline silica cristobalite and tridymite. Crystalline silica, quartz is also considered representative of diatomaceous earth, as they both consist mainly of silicon dioxide. Screening Assessment Conclusion – Crystalline silica, quartz, cristobalite and tridymite and diatomaceous earth are classified as tier 1 chemicals and require a hazard assessment only. 1 BACKGROUND Crystalline silica is a common mineral found in the earth's crust. Materials like sand, stone, concrete and mortar contain crystalline silica. It is also used to make products such as glass, pottery, ceramics, bricks and artificial stone. Silica, in the form of sand, is used as the main ingredient in sand casting for the manufacture of metallic components in engineering and other applications. The high melting point of silica enables it to be used in such applications. -

Minnesota's Mineral Resources
CHAPTER • 9 Minnesota's Mineral Resources IN MINNESOTA the production of iron ore is far more valuable economically than the total of all other mineral products, but im portant industries are based on Minnesota's other geological forma tions as well. Architectural, monumental, and structural stone are produced from granite, limestone, dolomite, and other Minnesota rocks. Gravel and sand are excavated and processed, and clay is used for many ceramic products. :Manganese in important amounts occurs in the iron ores of the Cuyuna district. Finally, although they are often not thought of as mineral products, two of our most im portant mineral resources are water and soil. The iron ores and mining operations of the Mesabi, Vermilion, and Cuyuna iron-bearing districts and of the southeastern lYlinnesota counties will be discussed in detail in later chapters, but a few sta tistics on Minnesota's iron ore industry may remind us how impor tant this geological heritage is. The following is an estimate of Min nesota's iron ore reserves, made on lYlay 1, 1961: Gross Tons Mesabi Range 500,799,179 Vermilion Range 9,755,974 Cuyuna Range 36,530,000 Fillmore County 'il,860,337 Total iron ore 549,945,490 172 MI NESOTA'S MINERAL RESOURCES The total production of iron ore in Minne ota to January 1, 1962, was 2,529,737,553 tons. Total taxes paid on iron ore to January 1, 1961 , were approximately $1,257,448,400, a very important source of funds for the state government. Slightly over 60 per cent of the total iron ore produced in the United States has come from l\1inne- ota. -

Symposium on Agate and Cryptocrystalline Quartz
Symposium on Agate and Cryptocrystalline Quartz September 10 – 13, 2005 Golden, Colorado Sponsored by Friends of Mineralogy, Colorado Chapter; Colorado School of Mines Geology Museum; and U.S. Geological Survey 2 Cover Photos {top left} Fortification agate, Hinsdale County, Colorado, collection of the Geology Museum, Colorado School of Mines. Coloration of alternating concentric bands is due to infiltration of Fe with groundwater into the porous chalcedony layers, leaving the impermeable chalcedony bands uncolored (white): ground water was introduced via the symmetric fractures, evidenced by darker brown hues along the orthogonal lines. Specimen about 4 inches across; photo Dan Kile. {lower left} Photomicrograph showing, in crossed-polarized light, a rhyolite thunder egg shell (lower left) a fibrous phase of silica, opal-CTLS (appearing as a layer of tan fibers bordering the rhyolite cavity wall), and spherulitic and radiating fibrous forms of chalcedony. Field of view approximately 4.8 mm high; photo Dan Kile. {center right} Photomicrograph of the same field of view, but with a 1 λ (first-order red) waveplate inserted to illustrate the length-fast nature of the chalcedony (yellow-orange) and the length-slow character of the opal CTLS (blue). Field of view about 4.8 mm high; photo Dan Kile. Copyright of articles and photographs is retained by authors and Friends of Mineralogy, Colorado Chapter; reproduction by electronic or other means without permission is prohibited 3 Symposium on Agate and Cryptocrystalline Quartz Program and Abstracts September 10 – 13, 2005 Editors Daniel Kile Thomas Michalski Peter Modreski Held at Green Center, Colorado School of Mines Golden, Colorado Sponsored by Friends of Mineralogy, Colorado Chapter Colorado School of Mines Geology Museum U.S. -

Stishovite and Seifertite in Lunar Meteorite Northwest Africa 4734
71st Annual Meteoritical Society Meeting (2008) 5058.pdf FIRST EVIDENCE OF HIGH PRESSURE SILICA: STISHOVITE AND SEIFERTITE IN LUNAR METEORITE NORTHWEST AFRICA 4734. H. Chennaoui Aoudjehane1-2, A. Jambon2 1Université Hassan II Aïn Chock, Laboratoire Géosciences, BP 5366 Maârif Casa- blanca Morocco (e-mail: [email protected]), 2Université Pierre et Marie Curie-Paris6 and IPGP Laboratoire MAGIE, Case 110, 4 place Jussieu, 75252 Paris France. Introduction: Silica is a rare phase in lunar rocks; it has been described as either quartz, cristobalite and/or tridymite [1]. Northwest Africa 4734, is an uncommon type of lunar rock, which may be launched paired with the LaPaz Icefield Lunar Mare basalts found in 2002-03 in Antarctica [2-6], it is a coarse grained rock of basaltic composition, exhibits a number of sig- nificant shock features, such as PDFs, extensive fracturation of pyroxene, impact melt pockets and transformation of plagioclase to maskelynite; silica is present as a minor phase. Analytical procedures: We studied the speciation of silica polymorphs to characterize the shock, using SEM imaging, Ra- man spectroscopy, CL imaging and spectroscopy. Further details can be found in [7]. Results: According to the CL spectra [7-9], cristobalite, tridymite, high-pressure silica glass, stishovite and seifertite, are all present. Special emphasis is made on stishovite and seifertite, which, like in shergottites, exhibit specific textural features [7]. Cathodoluminescence spectra characteristic of high-pressure sil- ica phases: glass, stishovite and seifertite have been recorded in addition to the original low-pressure phases. The remanence of cristobalite and tridymite underscores a significant heterogeneity of the shock supported by the rock. -

John S. White Mineral and Gem Collections GENERAL Nephrite Boulder – Trinity County, California Pyrite Navajun, Logroño, Spain 20-11-3
John S. White Mineral and Gem Collections GENERAL Nephrite boulder – Trinity County, California Pyrite Navajun, Logroño, Spain 20-11-3 12 cm Figured specimen (12) Beryl var. emerald – Crabtree Mountain emerald mine, Mitchell Co., N.C. G5-9-12 5 cm Ocean jasper – Cabamby mine, Majunga, Madagascar – G10-9-1 4.3 cm Ocean jasper – Cabamby mine, Majunga, Madagascar G11-2-3 4 cm Andalusite, variety chiastolite – China 10-2-43 2.7 cm Graphic granite – Madagascar 17-9-3 4.5 cm Garnet color suite – mixed localities G8-11-1 Sasha Siemel Beryl Jaguar hunter Governador Valadares & Minas Gerais, Brazil Mineral dealer 19-4-2 & 19-5-4 These specimens were sold by Sasha Siemel to friends of mine at a mineral show in Doylestown, PA, 1956 Gas bubble in fluorite Cave-in-Rock, Illinois 4-12-3 Russell Feather photo Regional Collection Pennsylvania – Maryland - Virginia Magnetite – Grace mine, Morgantown, PA 4-6-1 6.5 cm Rutile – Parkesburg, Chester County, PA 3-9-16 5 cm Dolomite - Ober & Binkley quarry, E. Petersburg, Lancaster Co., PA 17-2-6 10.5 cm Pyromorphite – Wheatley mine, Phoenixville, Chester Co., PA 6-6-9 9 cm Analcime & Apophyllite – Cornwall mine, Cornwall, Lebanon County, PA 20-10-15 10 cm Quartz – Reading anthracite mine, near St. Clair, Schuykill Co., PA 19-9-7 10 cm Fluorapatite & Actinolite – Silver Hill quarry, Brecknock Twp., Lancaster Co., PA 18-2-18 11.5 cm Wavellite – Mt. Pleasant Mills quarry, Perry Twp., Snyder Co., PA 18-2-19 4 cm Strontianite – Oak Hill quarry, Centre County, PA 21-11-1 5.5 cm Strontianite – Tonoloway limestone, Mt. -

Cristobalite Sio2 C 2001 Mineral Data Publishing, Version 1.2 ° Crystal Data: Tetragonal, Pseudocubic
Cristobalite SiO2 c 2001 Mineral Data Publishing, version 1.2 ° Crystal Data: Tetragonal, pseudocubic. Point Group: 422: As pseudo-octahedral crystals, to 4 mm, with 110 and 331 , rarely pseudocubic. Commonly dendritic to skeletal; as spherulites to sefveragl cm; ¯fbrougs or microcrystalline (\opal"), massive. Twinning: On 111 , common, interpenetrant, polysynthetic, repeated. f g Physical Properties: Tenacity: Brittle. Hardness = 6{7 D(meas.) = 2.32{2.36 D(calc.) = 2.33 Optical Properties: Transparent. Color: Colorless, white, milky white to yellowish; in transmitted light, colorless. Luster: Vitreous. Optical Class: Uniaxial ({). ! = 1.487 ² = 1.484 Cell Data: Space Group: P 41212: a = 4.9709(1) c = 6.9278(2) Z = 4 X-ray Powder Pattern: Synthetic. 4.05 (100), 2.485 (20), 2.841 (13), 3.135 (11), 1.870 (7), 2.465 (5), 2.118 (5) Chemistry: (1) SiO2 [99.13] TiO2 0.38 Al2O3 0.18 FeO 0.09 MnO < 0.02 MgO < 0.03 CaO < 0.02 Na2O 0.05 K2O 0.17 P2O5 < 0.03 Total [100.00] (1) Mare Imbrium, Moon; by electron microprobe, SiO2 by di®erence. Polymorphism & Series: Quartz, tridymite, coesite, and stishovite are polymorphs; inverts from high- or ¯-cristobalite at 268 ±C or below. Occurrence: In vesicles and lithophysae; a late-crystallizing phase in basaltic to rhyolitic volcanic rocks; from acid-sulfate-type hydrothermal alteration of volcanic rocks; precipitated by hot springs. By contact metamorphism of sandstone; developed during diagenesis, recrystallized from siliceous sedimentary rocks. Association: Tridymite, quartz, sanidine, anorthoclase, fayalite, magnetite, kaolinite, alunite, \opal." Distribution: On Cerro San Crist¶obal, near Pachuca, Hidalgo, and in the Sant¶³n mine, Santa Caterina, Guanajuato, Mexico. -

(Quartz) Silica, Sio2, Is a White Or Colorless Crystalline Compound
Silica (quartz) Silica, SiO2, is a white or colorless crystalline compound found mainly as quartz, sand, flint, and many other minerals. Silica is an important ingredient to manufacture a wide variety of materials. Quartz; Quartz is the most abundant silica mineral. Pure Quartz is colorless and transparent. It occurs in most igneous and practically all metamorphic and sedimentary rocks. It is used as a component of numerous industrial materials. Silicon (Si) has the atomic number 14 and is closely related to carbon. It is a relatively inert metalloid. Silicon is often used for microchips, glass, cement, and pottery. Silica is the most abundant mineral found in the crust of the earth. One of the most common uses of silica quarts is the manufacturer of glass. Silica is the fourteenth element on the periodic table. It can sometimes be found as the substance, quartz which is usually used in jewelry, test tubes, and when placed under pressure, generates an electrical charge. Quartz is the second most abundant mineral in the Earth's crust. It is a clear, glossy mineral with a hardness of 7 on the MOHS scale. Silica, Sa,is a component of glass and concrete. A form of Silica commonly known as quartz, Silica tetrahedra, is the second most common mineral in the earth's crust, it comes in many different forms. Silica is a compound of silicon and oxygen. Earth's outer crust contains 59% of this material. It has three major rock forms, which are quartz, tridymite, and cristobalite. Silica, commonly known in the form of quartz, is the dioxide form of silicon, SiO2. -

Discovery of Hardest Known Oxide
SCIENTIFIC CORRESPONDENCE hardness of stishovite has been reported Discovery of hardest known oxide to be 17-20.8 GPa along different direc tions7, but the sample used in this case SIR - Microhardness measurements on and is metastable under normal condi had been synthesized at about 9.5-10 GPa synthesized samples of stishovite, a high tions7; its bulk modulus, 298 GPa (ref. 8), and 1,200-1,400 °C. The transformation pressure phase of silica, show that it is the is significantly greater than that of alumi was not complete at this pressure, as later hardest oxide yet discovered. Among na, 252 GPa, which is itself a hard oxide. shown 11• The small amount of lower-pres polycrystalline materials, its hardness (33 Here, we report microhardness measure sure phases present drastically modified gigapascals, GPa) rivals those of the hard ments on synthesized stishovite. the indentation results. est materials. Despite many searchesl-4, We performed synthesis experiments Polycrystalline stishovite is now the no material with a measured hardness using a 1,200-ton uniaxial MA-8 multi hardest oxide known; it is harder than comparable to diamond or cubic boron anvil apparatus (see ref. 9 for method), alumina and boron oxides12• Other super nitride has been identified until now. taking Raman and X-ray diffraction (see hard polycrystalline materials include dia Hardness (H) of ionic and covalent ref. 10 for image plate system) measure mond and cubic boron nitride compacts; materials increases with bulk modulus1- 5_ ments. Microprobe analysis showed only their hardness is much lower than that Diamond has the highest known bulk silicon in the investigated region. -

Silicic Volcanism on Mars Evidenced by Tridymite in High-Sio2 Sedimentary Rock at Gale Crater Richard V
Silicic volcanism on Mars evidenced by tridymite in high-SiO2 sedimentary rock at Gale crater Richard V. Morrisa,1, David T. Vanimanb, David F. Blakec, Ralf Gellertd, Steve J. Chiperae, Elizabeth B. Rampef, Douglas W. Minga, Shaunna M. Morrisong, Robert T. Downsg, Allan H. Treimanh, Albert S. Yeni, John P. Grotzingerj,1, Cherie N. Achillesg, Thomas F. Bristowc, Joy A. Crispi, David J. Des Maraisc, Jack D. Farmerk, Kim V. Fendrichg, Jens Frydenvangl,m, Trevor G. Graffn, John-Michael Morookiani, Edward M. Stolperj, and Susanne P. Schwenzerh,o aNASA Johnson Space Center, Houston, TX 77058; bPlanetary Science Institute, Tucson, AZ 85719; cNASA Ames Research Center, Moffitt Field, CA 94035; dDepartment of Physics, University of Guelph, Guelph, ON, Canada N1G 2W1; eChesapeake Energy, Oklahoma City, OK 73118; fAerodyne Industries, Houston, TX 77058; gDepartment of Geosciences, University of Arizona, Tucson, AZ 85721; hLunar and Planetary Institute, Houston, TX 77058; iJet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109; jDivision of Geological and Planetary Sciences, California Institute of Technology, Pasadena, CA 91125; kSchool of Earth and Space Exploration, Arizona State University, Tempe, AZ 85287; lLos Alamos National Laboratory, Los Alamos, NM 87545; mNiels Bohr Institute, University of Copenhagen, 2100 Copenhagen, Denmark; nJacobs, Houston, TX 77058; and oDepartment of Environment, Earth and Ecosystems, The Open University, Milton Keynes MK7 6AA, United Kingdom Contributed by John P. Grotzinger, May 5, 2016 (sent for review March 18, 2016); reviewed by Jon Blundy, Robert M. Hazen, and Harry Y. McSween) Tridymite, a low-pressure, high-temperature (>870 °C) SiO2 poly- (1), where three drill samples were analyzed by CheMin [Confi- morph, was detected in a drill sample of laminated mudstone (Buck- dence Hills, Mojave2, and Telegraph Peak (2)]. -

Minerals Found in Michigan Listed by County
Michigan Minerals Listed by Mineral Name Based on MI DEQ GSD Bulletin 6 “Mineralogy of Michigan” Actinolite, Dickinson, Gogebic, Gratiot, and Anthonyite, Houghton County Marquette counties Anthophyllite, Dickinson, and Marquette counties Aegirinaugite, Marquette County Antigorite, Dickinson, and Marquette counties Aegirine, Marquette County Apatite, Baraga, Dickinson, Houghton, Iron, Albite, Dickinson, Gratiot, Houghton, Keweenaw, Kalkaska, Keweenaw, Marquette, and Monroe and Marquette counties counties Algodonite, Baraga, Houghton, Keweenaw, and Aphrosiderite, Gogebic, Iron, and Marquette Ontonagon counties counties Allanite, Gogebic, Iron, and Marquette counties Apophyllite, Houghton, and Keweenaw counties Almandite, Dickinson, Keweenaw, and Marquette Aragonite, Gogebic, Iron, Jackson, Marquette, and counties Monroe counties Alunite, Iron County Arsenopyrite, Marquette, and Menominee counties Analcite, Houghton, Keweenaw, and Ontonagon counties Atacamite, Houghton, Keweenaw, and Ontonagon counties Anatase, Gratiot, Houghton, Keweenaw, Marquette, and Ontonagon counties Augite, Dickinson, Genesee, Gratiot, Houghton, Iron, Keweenaw, Marquette, and Ontonagon counties Andalusite, Iron, and Marquette counties Awarurite, Marquette County Andesine, Keweenaw County Axinite, Gogebic, and Marquette counties Andradite, Dickinson County Azurite, Dickinson, Keweenaw, Marquette, and Anglesite, Marquette County Ontonagon counties Anhydrite, Bay, Berrien, Gratiot, Houghton, Babingtonite, Keweenaw County Isabella, Kalamazoo, Kent, Keweenaw, Macomb, Manistee, -

Diamond Dan's Mineral Names Dictionary
A Dictionary of Mineral Names By Darryl Powell Mineral Names What do they mean? Who created them? What can I learn from them? This mineral diction‐ ary is unique because it is illustrated, both with mineral drawings as well as pictures of people and places after which some minerals are named. The people pictured on this page have all made a con‐ tribution to what is formally called “mineral nomenclature.” Keep reading and you will discover who they are and what they did. In 1995, Diamond Dan Publications pub‐ lished its first full book, “A Mineral Collector’s Guide to Common Mineral Names: Their Ori‐ gins & Meanings.” Now it is twenty years later. What you will discover in this issue and in the March issue is a re‐ vised and improved version of this book. This Mineral Names Dictionary contains mineral names that the average mineral collector will encounter while collecting minerals, attending shows and visiting museum displays. In addition to the most common min‐ eral names, there are some unofficial names which you will still find on labels. Each mineral name has a story to tell or a lesson to teach. If you wanted to take the time, each name could become a topic to study. Armalcolite, for example, could quickly be‐ come a study of a mineral, first discovered on the moon, and brought back to earth by the astronauts Armstrong, Aldrin and Collins (do you see parts of their names in this mineral name?) This could lead you to a study of American astronauts landing on the moon, what it took to get there and what we discovered by landing on the moon. -
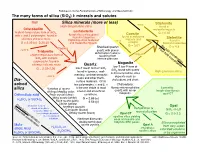
Silica Minerals (More Or Less) Dis- Solved Silica the Many Forms Of
Railsback's Some Fundamentals of Mineralogy and Geochemistry The many forms of silica (SiO2) I: minerals and solutes Melt Silica minerals (more or less) ~80 kb Stishovite High-temperature silica found in Cristobalite meteorite impacts Lechatelierite highest-temperature form of SiO2, Coesite G = 4.35 with ! and " polymorphs, found in fused silica (silica glass) found in fulgurites found in meteorite siliceous volcanic rocks Siefertite (lightning-strike features) ~20 kb impacts and found in G = 2.32 (!) 2.20 (") and meteorite impacts. eclogite Martian meteorites G = 3.01 Six-fold Gcoordination = 4.3 Cooling Shocked quartz: Four-fold coordination ~1470°C Tridymite quartz with planar deformation features Impact a high-temperature form of resulting from SiO2 with multiple intense pressure polymorphs, found in Moganite siliceous volcanic rocks Quartz low-T low-P form of low-T low-P form of SiO G = 2.22-2.26 2 SiO found with quartz found in igneous, sedi- 2 High-pressure silica in microcrystalline silica mentary, and metamorphic ~870°C deposits such as rocks and other Earth- chalcedony and chert. Dis- surface materials. Of its solved two polymorphs, ! and ", ! Chalcedony: silica Varieties of quartz is the one stable at most fibrous microcrystalline Lussatite: crustal and all surficial quartz with lesser length-slow fibrous distinguished by color: moganite. Orthosilicic acid Rock crystal (clear) conditions. opal-CT Milky quartz (white) G = 2.65 (!) H4SiO4 or Si(OH)4 Rose quartz (pink) 2.53 (") Four-fold coordination Citrine (yellow) Monomer is most Amethyst (purple) Opal Three-fold coordination abundant in dilute Dehydration & Cairngorm (brown) SiO · nH O solutions; dimer is recrystallization 2 2 increasingly abundant Smoky quartz (black) Opal CT G = 2.0-2.3 in concentrated opalline silica yielding solutions.