Topographic Position and Landforms Analysis Andrew D. Weiss, The
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

RECREATION GUIDE 2021 1 Your BUTTE FAMILY IS IMPORTANT to Our BUTTE FAMILY
2021 Kids Summer Fun Events Pg.27 Pg.8-9 Brought to you by BUTTE RECREATION GUIDE 2021 1 Your BUTTE FAMILY IS IMPORTANT TO our BUTTE FAMILY townpump.com 2 BUTTE RECREATION GUIDE 2021 BUTTE RECREATION GUIDE 2021 3 OUR MISSION e Butte-Silver Bow Parks and Recreation Department is committed to improving our community’s health, stability, beauty, and quality of life by providing outstanding parks, trails, recreational facilities and leisure opportunities for all of our citizens. Butte-Silver Bow Parks & Recreation at a glance: • More than two dozen parks (many with pavilions that can be reserved), numerous playgrounds, a 9 hole regulation golf course, a par-3 golf course, a clubhouse with golf simulators, two disc golf courses, a splash pad, and a wading pool • Ridge Waters: A family water park featuring two water slides, a lazy river, a zero depth entry children’s area, a climbing wall, a diving board, swimming lanes, rentable cabanas, and a concession stand • A new destination playground at Stodden Park • An extensive urban and rural trail system • ompson Park: e only dually managed municipal/National Forest Service park in the nation • Adult and youth programming, which include: volleyball, softball and pickleball and more • Two historic mine yards that are now event facilities • Community-wide special events CONTENTS Parks & Recreation Fast Facts…Page 6 Butte Arborist…Page 7 Ridge Waters…Page 8 We’re on the web! Stodden Park…Page 10 butteparksandrec.com ridgewaters.com Popular Urban Parks…Page 11 highlandviewgolf.com Recreational Facilities…Page 16 Find us on Facebook, Twitter and Instagram! Mine Yards…Page 18 Rural Parks & Recreation Near Butte…Page 20 Thompson Park Map…Page 22 Butte Urban Map…Page 23 @ButteParks @ButteSilverBow @ButteParksandRec Highland View Golf Course…Page 25 Summer Fun Youth Events…Page 27 Regional Outdoor Opportunities… On the cover: Page 29 Cyclist in Thompson Park. -

Part 629 – Glossary of Landform and Geologic Terms
Title 430 – National Soil Survey Handbook Part 629 – Glossary of Landform and Geologic Terms Subpart A – General Information 629.0 Definition and Purpose This glossary provides the NCSS soil survey program, soil scientists, and natural resource specialists with landform, geologic, and related terms and their definitions to— (1) Improve soil landscape description with a standard, single source landform and geologic glossary. (2) Enhance geomorphic content and clarity of soil map unit descriptions by use of accurate, defined terms. (3) Establish consistent geomorphic term usage in soil science and the National Cooperative Soil Survey (NCSS). (4) Provide standard geomorphic definitions for databases and soil survey technical publications. (5) Train soil scientists and related professionals in soils as landscape and geomorphic entities. 629.1 Responsibilities This glossary serves as the official NCSS reference for landform, geologic, and related terms. The staff of the National Soil Survey Center, located in Lincoln, NE, is responsible for maintaining and updating this glossary. Soil Science Division staff and NCSS participants are encouraged to propose additions and changes to the glossary for use in pedon descriptions, soil map unit descriptions, and soil survey publications. The Glossary of Geology (GG, 2005) serves as a major source for many glossary terms. The American Geologic Institute (AGI) granted the USDA Natural Resources Conservation Service (formerly the Soil Conservation Service) permission (in letters dated September 11, 1985, and September 22, 1993) to use existing definitions. Sources of, and modifications to, original definitions are explained immediately below. 629.2 Definitions A. Reference Codes Sources from which definitions were taken, whole or in part, are identified by a code (e.g., GG) following each definition. -

South Carolina Landform Regions (And Facts About Landforms) Earth Where Is South Carolina? North America United States of America SC
SCSouth Carolina Landform Regions (and facts about Landforms) Earth Where is South Carolina? North America United States of America SC Here we are! South Carolina borders the Atlantic Ocean. SC South Carolina Landform Regions Map Our state is divided into regions, starting at the mountains and going down to the coast. Can you name these? Blue Ridge Mountains Landform Regions SC The Blue Ridge Mountain Region is only 2% of the South Carolina land mass. Facts About the Blue Ridge Mountains . ◼ It is the smallest of the landform regions ◼ It includes the state’s highest point: Sassafras Mountain. ◼ The Blue Ridge Mountains are part of the Appalachian Mountain Range Facts About the Blue Ridge Mountains . ◼ The Blue Ridge Region is mountainous and has many hardwood forests, streams, and waterfalls. ◼ Many rivers flow out of the Blue Ridge. Blue Ridge Mountains, SC Greenville Spartanburg Union Greenwood Rock Hill Abbeville Piedmont Landform Regions SC If you could see the Piedmont Region from space and without the foliage, you would notice it is sort of a huge plateau. Facts About the Piedmont Region . ◼ The Piedmont is the largest region of South Carolina. ◼ The Piedmont is often called The Upstate. Facts About the Piedmont Region . ◼ It is the foothills of the mountains and includes rolling hills and many valleys. ◼ Piedmont means “foot of the mountains” ◼ Waterfalls and swift flowing rivers provided the water power for early mills and the textile industry. Facts About the Piedmont Region . ◼ The monadnocks are located in the Piedmont. ◼ Monadnocks – an isolated or single hill made of very hard rock. -

Street Names - in Alphabetical Order
Street Names - In Alphabetical Order District / MC-ID NO. Street Name Location County Area Aalto Place Sumter - Unit 692 (Villa San Antonio) 1 Sumter County Abaco Path Sumter - Unit 197 9 Sumter County Abana Path Sumter - Unit 206 9 Sumter County Abasco Court Sumter - Unit 821 (Mangrove Villas) 8 Sumter County Abbeville Loop Sumter - Unit 80 5 Sumter County Abbey Way Sumter - Unit 164 8 Sumter County Abdella Way Sumter - Unit 180 9 Sumter County Abdella Way Sumter - Unit 181 9 Sumter County Abel Place Sumter - Unit 195 10 Sumter County Aber Lane Sumter - Unit 967 (Ventura Villas) 10 Sumter County SE 84TH Abercorn Court Marion - Unit 45 4 Marion County Abercrombie Way Sumter - Unit 98 5 Sumter County Aberdeen Run Sumter - Unit 139 7 Sumter County Abernethy Place Sumter - Unit 99 5 Sumter County Abner Street Sumter - Unit 130 6 Sumter County Abney Avenue VOF - Unit 8 12 Sumter County Abordale Lane Sumter - Unit 158 8 Sumter County Acorn Court Sumter - Unit 146 7 Sumter County Acosta Court Sumter - Unit 601 (Villa De Leon) 2 Sumter County Adair Lane Sumter - Unit 818 (Jacaranda Villas) 8 Sumter County Adams Lane Sumter - Unit 105 6 Sumter County Adamsville Avenue VOF - Unit 13 12 Sumter County Addison Avenue Sumter - Unit 37 3 Sumter County Adeline Way Sumter - Unit 713 (Hillcrest Villas) 7 Sumter County Adelphi Avenue Sumter - Unit 151 8 Sumter County Adler Court Sumter - Unit 134 7 Sumter County Adriana Way Sumter - Unit 711 (Adriana Villas) 7 Sumter County Adrienne Way Sumter - Unit 176 9 Sumter County Adrienne Way Sumter - Unit 949 (Megan -

A Geomorphic Classification System
A Geomorphic Classification System U.S.D.A. Forest Service Geomorphology Working Group Haskins, Donald M.1, Correll, Cynthia S.2, Foster, Richard A.3, Chatoian, John M.4, Fincher, James M.5, Strenger, Steven 6, Keys, James E. Jr.7, Maxwell, James R.8 and King, Thomas 9 February 1998 Version 1.4 1 Forest Geologist, Shasta-Trinity National Forests, Pacific Southwest Region, Redding, CA; 2 Soil Scientist, Range Staff, Washington Office, Prineville, OR; 3 Area Soil Scientist, Chatham Area, Tongass National Forest, Alaska Region, Sitka, AK; 4 Regional Geologist, Pacific Southwest Region, San Francisco, CA; 5 Integrated Resource Inventory Program Manager, Alaska Region, Juneau, AK; 6 Supervisory Soil Scientist, Southwest Region, Albuquerque, NM; 7 Interagency Liaison for Washington Office ECOMAP Group, Southern Region, Atlanta, GA; 8 Water Program Leader, Rocky Mountain Region, Golden, CO; and 9 Geology Program Manager, Washington Office, Washington, DC. A Geomorphic Classification System 1 Table of Contents Abstract .......................................................................................................................................... 5 I. INTRODUCTION................................................................................................................. 6 History of Classification Efforts in the Forest Service ............................................................... 6 History of Development .............................................................................................................. 7 Goals -

5 Regions of Virginia Bordering States Major Rivers & Cities Bordering
5 Regions of Virginia Bordering States West to East All Virginia Bears Play Tag Appalachian Plateau Valley & Ridge Never Taste Ketchup Without Mustard Blue Ridge Piedmont North Carolina Tidewater/Coastal Plain Tennessee Kentucky West Virginia Maryland Major Rivers & Cities Bordering Bodies of Water North to South Alex likes Potatoes Alexandria (and DC) are on the Potomac River. Fred likes to Rap Fredericksburg is on the Rappahannock River Chesapeake Bay Yorktown is on the York River Separates mainland Atlantic King James was Rich. VA and Eastern Shore Ocean Jamestown & Richmond are on the James River. Eastern Shore Rivers Eastern Shore Peninsula Flow into the Chesapeake Bay Source of food Pathway for exploration and settlement Chesapeake Bay Provided a safe harbor Was a source of food and transportation Atlantic Ocean Provided transportation Peninsula: links between Virginia and other places (Europe, Piece of land bordered by Africa, Caribbean) water on 3 sides Fall Line Tidewater - Coastal Plain Region Low, flat land; East of the Fall Land; Includes Eastern Shore; Natural Border between Waterfalls prevent near Atlantic Ocean and Chesapeake Bay Piedmont & Tidewater further travel on Regions the rivers. Piedmont Region Relative Location The mouse is next to the box. The ball is near the box. West of the Fall Line Means "Land at the Foot of the Mountain" Blue Ridge Mountain Region Valley and Ridge Region Old, Rounded Mountains West of Blue Ridge Region Source of Many Rivers Includes the Great Valley of Virginia Piedmont to East/Valley & Ridge to West Valleys separated by ridges Part of Appalachian Mountain System Part of Appalachian Mountain System Appalachian Plateau Region Plateau Area of elevated land that is flat on top Located in Southwest Virginia Only Small Part of Plateau Located in Virginia Dismal Swamp and Valley, Ridge Definition Lake Drummond Ridge: chain of hills Located in Tidewater/Coastal Plain Region Dismal Swamp: Surveyed by George Washington; lots of wildlife Lake Drummond: Shallow lake surrounded by Valley: land between hills swamp . -

Cumberland Plateau Geological History
National Park Service U.S. Department of the Interior Big South Fork National River and Recreation Area Oneida, Tennessee Geology and History of the Cumberland Plateau Geological History Rising over 1000 feet above the region around it, the Cumberland Plateau is a large, flat-topped tableland. Deceptively rugged, the Plateau has often acted as a barrier to man and nature’s attempts to overcome it. The Plateau is characterized by rugged terrain, a moderate climate, and abundant rainfall. Although the soils are typically thin and infertile, the area was once covered by a dense hardwood forest equal to that of the Appalachians less than sixty miles to the east. As a landform, this great plateau reaches from north-central Alabama through Tennessee and Kentucky and Pennsylvania to the western New York border. Geographers call this landform the Appalachian Plateau, although it is known by various names as it passes through the differ ent regions. In Tennessee and Kentucky, it is called the Cumberland Plateau. Within this region, the Cumberland River and its tributaries are formed. A view from any over- look quickly confirms that the area is indeed a plateau. The adjoining ridges are all the same height, presenting a flat horizon. The River Systems The Clear Fork River and the New River come together to form the Big South Fork of the Cumberland River, the third largest tributary to the Cumberland. The Big South Fork watershed drains an area of 1382 square Leatherwood Ford in the evening sun miles primarily in Scott, Fentress, and Morgan counties in Tennessee and Wayne and Overlooks McCreary counties in Kentucky. -

R6 Geomorphology Legend and Glossary
Geomorphology of the Pacific Northwest Legend and Glossary Definitions and Descriptions of Terms Used in the Mapping of Landforms, Landform Groups, and Landform Associations in Region Six, Forest Service Jay S. Noller Oregon State University Corvallis, Oregon Sarah J. Hash Forest Service Bend, Oregon Karen Bennett Forest Service Portland, Oregon December 2013 ver. 0.7 DRAFT Note to the Reader This provisional, draft text presents and briefly describes the terms used in the preparation of a map of landform groups covering all forests within Region Six of the US Forest Service. Formal definition of map units is pending completion of this map and review thereof by all of the forests in Region Six. Map unit names appended to GIS shapefiles are concatenations of terms defined herein and are meant to be objective descriptors of the landscape within each map unit boundary. These map unit names have yet to undergo a final vetting and culling to reduce complexity, redundancy or obfuscation unintentionally resulting from map creation activities. Any omissions or errors in this draft document are the responsibility of its authors. Rev. 06 on 05December2013 by Jay Noller 2 Geomorphology of the Pacific Northwest – Map Legend Term Description Ancient Volcanoes Landform groups suggestive of a deeply eroded volcano. Typically a central hypabyssal or shallow plutonic rocks are present in central (core) area of the relict volcano. Apron Footslope to toeslope positions of volcanoes to mountain ranges. Synonymous with bajada in an alluvial context. Ballena Distinctively round-topped, parallel to sub-parallel ridgelines and intervening valleys that have an overall fan-shaped or distributary drainage pattern. -

Alphabetical Glossary of Geomorphology
International Association of Geomorphologists Association Internationale des Géomorphologues ALPHABETICAL GLOSSARY OF GEOMORPHOLOGY Version 1.0 Prepared for the IAG by Andrew Goudie, July 2014 Suggestions for corrections and additions should be sent to [email protected] Abime A vertical shaft in karstic (limestone) areas Ablation The wasting and removal of material from a rock surface by weathering and erosion, or more specifically from a glacier surface by melting, erosion or calving Ablation till Glacial debris deposited when a glacier melts away Abrasion The mechanical wearing down, scraping, or grinding away of a rock surface by friction, ensuing from collision between particles during their transport in wind, ice, running water, waves or gravity. It is sometimes termed corrosion Abrasion notch An elongated cliff-base hollow (typically 1-2 m high and up to 3m recessed) cut out by abrasion, usually where breaking waves are armed with rock fragments Abrasion platform A smooth, seaward-sloping surface formed by abrasion, extending across a rocky shore and often continuing below low tide level as a broad, very gently sloping surface (plain of marine erosion) formed by long-continued abrasion Abrasion ramp A smooth, seaward-sloping segment formed by abrasion on a rocky shore, usually a few meters wide, close to the cliff base Abyss Either a deep part of the ocean or a ravine or deep gorge Abyssal hill A small hill that rises from the floor of an abyssal plain. They are the most abundant geomorphic structures on the planet Earth, covering more than 30% of the ocean floors Abyssal plain An underwater plain on the deep ocean floor, usually found at depths between 3000 and 6000 m. -

Glacial Geology
Wisconsin Department of Transportation Geotechnical Manual Chapter 2 Geology of Wisconsin Section 3 Glacial Geology Glaciation has had a pronounced effect on the landscape, subsurface strata, and soils of the state. This section will examine the occurrences, movements, extent, and impacts of glaciation on the physical surface of Wisconsin. A number of terms and definitions associated with glaciers and glacial geology will also be presented. 2-3.1 Terms and Definitions An understanding of the following list of terms is important to understand glacial history and processes: Glacier A large ice mass flowing due to its own weight and gravity. Continental glaciers covered thousands of square miles of the earth’s surface and were 1 to 2 miles thick in some areas. Drift A general term for glacially deposited material. Till A heterogeneous mixture of soil and rock fragments carried and deposited by a glacier. End Moraine A distinct ridge of till accumulated at the line of maximum advance of a glacier. Also called a terminal moraine. Recessional Distinct ridges of till formed behind end moraines as the glacier receeded. These Moraine features mark positions of glacial stagnation or renewed advance. Ground Till deposited in an indistinct manner as the glacier receded. Often Moraine consists of a relatively thin blanket of material marked by low hills and swales. Glacial Lakes Lakes that were formed along the front of a glacier due to the general contour of the land and the blockage of normal drainage channels. These lakes disappeared as the glaciers receded. Lacustrine Material deposited in glacial lakes forming the bed of those lakes. -

Updated Wine List.Xlsb
Straight Up and On the Rocks Planter's Punch Myers Dark Rum, Orange Juice, Pineapple Juice, & Grenadine, Served on the Rocks 8 Tea Tini Stoli Oranj with a Splash of Southern Sweet Tea, Orange, Lemon & Lime Juices, Served 9 Straight Up in a Sugar Rimmed Martini Glass Pomegranate Margarita Patrón Silver Tequila, Fresh Pomegranate juice, Fresh Squeezed Lime, and a 13 Float of Pama Liqueur, Served on the Rocks in a Sugar Rimmed Glass Gin Blossoms Hendrix Gin, Saint Germain Elderflower Liqueur, Splash of Fresh Squeezed Lemon Juice 12 and Soda Water, Served on the Rocks The Rudy Cardinal Cardinal American Dry Gin and Jack Rudy Tonic, Served on the Rocks finished with 12 a Slice of Lemon Carolina Cocktail Local Firefly "Sweet Tea" Vodka, Fresh Squeezed Lemonade, Splash of Soda, Served over 10 Crushed Ice Sidecar Courvoisier, Triple Sec, Fresh Lemon, Served Straight Up in a Sugar Rimmed Martini Glass 9 Southern Manhattan Knob Creek Bourbon, Southern Comfort Liqueur, Angostura Bitters, Garnished 13 with Brandy Soaked Cherries, Served on the Rocks Bourbon Honey Old Fashion Wild Turkey Bourbon, Wild Turkey Honey Liqueur, Muddled Fruit, 11 Angostura Bitters, Pure Cane Sugar, with a Splash of Soda, Served on the Rocks WINES BY THE GLASS Champagne & Sparkling Avinyó "Reserva" Cava Rosé, Penedès N/V 11 Adami Prosecco, Brut, Treviso N/V 11 Veuve Clicquot "Yellow Label", Brut, Reims N/V 19 Laurent‐Perrier, Brut N/V 15 Dumont Pere et Fils, Brut Rosé, Aube N/V 19 White & Rosé Chardonnay, Steele Wines "Steele Cuvée", California 2013 13 Chardonnay, Domaine -
Site 2 Table Rock
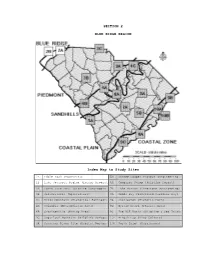
SECTION 2 BLUE RIDGE REGION Index Map to Study Sites 2A Table Rock (Mountains) 5B Santee Cooper Project (Engineering & 2B Lake Jocassee Region (Energy Producti 6A Congaree Swamp (Pristine Forest) 3A Forty Acre Rock (Granite Outcropping 7A Lake Marion (Limestone Outcropping) 3B Silverstreet (Agriculture) 8A Woods Bay (Preserved Carolina Bay) 3C Kings Mountain (Historical Battlegrou 9A Charleston (Historic Port) 4A Columbia (Metropolitan Area) 9B Myrtle Beach (Tourist Area) 4B Graniteville (Mining Area) 9C The ACE Basin (Wildlife & Sea Island lt ) 4C Sugarloaf Mountain (Wildlife Refuge) 10A Winyah Bay (Rice Culture) 5A Savannah River Site (Habitat Restorat 10B North Inlet (Hurricanes) TABLE OF CONTENTS FOR SECTION 2 BLUE RIDGE REGION - Index Map to Blue Ridge Study Sites - Table of Contents for Section 2 - Power Thinking Activity - "Mayday!, Mayday!, Mayday!" - Performance Objectives - Background Information - Description of Landforms, Drainage Patterns, and Geologic Processes p. 2-2 . - Characteristic Landforms of the Blue Ridge p. 2-2 . - Geographic Features of Special Interest p. 2-3 . - Blue Ridge Rock Types p. 2-3 . - Blue Ridge--Piedmont Boundary p. 2-4 . - Fracturing, Folding, and Uplift of the Blue Ridge - Influence of Topography on Historical Events and Cultural Trends p. 2-5 . - Native American Folklore p. 2-5 . - story - "Legend of Little Deer" p. 2-5 . - Traditional Scottish Ballads of the Blue Ridge p. 2-6 . - story - "Bonny Barbara Allan" p. 2-6 . - Ellicott's Rock p. 2-7 . - Mountains as Recreational Areas p. 2-7 . - Tourist Attractions - Natural Resources, Land Use, and Environmental Concerns p. 2-9 . - Climate Influences Land Use p. 2-9 . - Trout Streams p.