Cache Attacks and Countermeasures: the Case of AES 2005-08-14
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Taxonomy of Linux Kernel Vulnerability Solutions
Taxonomy of Linux Kernel Vulnerability Solutions Serguei A. Mokhov Marc-Andre´ Laverdiere` Djamel Benredjem Computer Security Laboratory Computer Security Laboratory Computer Security Laboratory Concordia Institute for Concordia Institute for Concordia Institute for Information Systems Engineering Information Systems Engineering Information Systems Engineering Concordia University, Concordia University, Concordia University, Montreal, Quebec, Canada Montreal, Quebec, Canada Montreal, Quebec, Canada Email: [email protected] Email: ma [email protected] Email: d [email protected] Abstract—This paper presents the results of a case study on C programs in general, as well as statistics on their relative software vulnerability solutions in the Linux kernel. Our major importance. We also introduce a new methodology to track contribution is the introduction of a classification of methods used the patch solving a security issue based only on the contents to solve vulnerabilities. Our research shows that precondition validation, error handling, and redesign are the most used of the security advisory. methods in solving vulnerabilities in the Linux kernel. This The paper is organized as follows: we examine previous contribution is accompanied with statistics on the occurrence work that was done regarding Linux and C security in of the different types of vulnerabilities and their solutions that Section II, followed by a description of the methodology we observed during our case study, combined with example used in order to obtain the solutions to the vulnerabilities in source code patches. We also combine our findings with existing programming guidelines to create the first security-oriented Section III. Afterwards, in Section IV, we show our results, coding guidelines for the Linux kernel. -

Cryptographic File Systems
Cryptographic Filesystems Background and Implementations for Linux and OpenBSD Background ● Loop device primer ● Keys, cipher modes, salting, key hashing ● Journaling file systems and encrypted swap ● Offset, sizelimit, hard/soft block size paramters explained ● Issues with software suspend Loopback Primer /dev/hda1 losetup /dev/loop0 myloop.dat /dev/loop0 /dev/hda2 losetup /dev/loop1 \ /dev/hda2 Filesystem with various /dev/loop1 files and directories Loopback Primer G76g(*gF *^tF0OB( 6g)%)f5( /dev/loop0 *&(*6bP( Dear Bob, this is the message ● The loopback device supports cryptographic transforms ● Knowing the key reveals a filesystem within a normal file (or block device) Keys ● Encryption with user supplied key ● Encryption with hashed key – rmd160, sha256, sha384, sha512, ... ● Using multiple keys (typically 64) – every sector (512b) uses different key Basic block cipher modes ● Currently only ECB (Electronic Code Book) and CBC (Cipher Block Chaining) widely supported ● ECB directly encipher plaintext – Same plaintext block always encrypts to same ciphertext. Is considered weak. ● CBC uses the previous block as IV – Basically solves ECB's dictionary problem – Only provides very limited integrity Key iterations and salt ● Key can be hashed 1000 times – significantly slows down brute force attack on password ● Salt is a string appended to the password – slows down brute force attack on password – poor man's two factor authentication Journaling ● Fine on device backed loop device ● Avoid on file backed loop devices – The VM can write -

Cryptographic File Systems Performance: What You Don't Know Can Hurt You Charles P
Cryptographic File Systems Performance: What You Don't Know Can Hurt You Charles P. Wright, Jay Dave, and Erez Zadok Stony Brook University Appears in the proceedings of the 2003 IEEE Security In Storage Workshop (SISW 2003) Abstract interact with disks, caches, and a variety of other com- plex system components — all having a dramatic effect Securing data is more important than ever, yet cryp- on performance. tographic file systems still have not received wide use. In this paper we perform a real world performance One barrier to the adoption of cryptographic file systems comparison between several systems that are used is that the performance impact is assumed to be too high, to secure file systems on laptops, workstations, and but in fact is largely unknown. In this paper we first moderately-sized file servers. We also emphasize multi- survey available cryptographic file systems. Second, programming workloads, which are not often inves- we perform a performance comparison of a representa- tigated. Multi-programmed workloads are becoming tive set of the systems, emphasizing multiprogrammed more important even for single user machines, in which workloads. Third, we discuss interesting and counterin- Windowing systems are often used to run multiple appli- tuitive results. We show the overhead of cryptographic cations concurrently. We expect cryptographic file sys- file systems can be minimal for many real-world work- tems to become a commodity component of future oper- loads, and suggest potential improvements to existing ating systems. systems. We have observed not only general trends with We present results from a variety of benchmarks, an- each of the cryptographic file systems we compared but alyzing the behavior of file systems for metadata op- also anomalies based on complex interactions with the erations, raw I/O operations, and combined with CPU operating system, disks, CPUs, and ciphers. -

New Methods in Hard Disk Encryption
New Methods in Hard Disk Encryption Clemens Fruhwirth <[email protected]> Institute for Computer Languages Theory and Logic Group Vienna University of Technology July 18, 2005 Abstract This work investigates the state of the art in hard disk cryptography. As the choice of the cipher mode is essential for the security of hard disk data, we discuss the recent cipher mode developments at two standardisation bodies, NIST and IEEE. It is a necessity to consider new developments, as the most common cipher mode – namely CBC – has many security problems. This work devotes a chapter to the analysis of CBC weaknesses. Next to others, the main contributions of this work are (1) efficient algorithms for series of multiplications in a finite field (Galois Field), (2) analysis of the security of password-based cryptography with respect to low entropy attacks and (3) a design template for secure key management, namely TKS1. For the latter, it is assumed that key management has to be done on regular user hardware in the absence of any special security hardware like key tokens. We solve the problems arising from magnetic storage by introducing a method called anti-forensic information splitter. This work is complemented by the presentation of a system implementing a variant of TKS1. It is called LUKS and it was developed and implemented by the author of this work. Contents Preface v 1 Introduction 1 2 Design ingredients 3 2.1 The many faces of n ........................ 3 2.2 Galois Field arithmetic . 4 2.3 Algorithms for GF(2η)....................... 9 2.4 Sequences of multiplications in GF(2η) . -

Efficient Cache Attacks on AES, and Countermeasures
J. Cryptol. (2010) 23: 37–71 DOI: 10.1007/s00145-009-9049-y Efficient Cache Attacks on AES, and Countermeasures Eran Tromer Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, 32 Vassar Street, G682, Cambridge, MA 02139, USA [email protected] and Department of Computer Science and Applied Mathematics, Weizmann Institute of Science, Rehovot 76100, Israel Dag Arne Osvik Laboratory for Cryptologic Algorithms, Station 14, École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland dagarne.osvik@epfl.ch Adi Shamir Department of Computer Science and Applied Mathematics, Weizmann Institute of Science, Rehovot 76100, Israel [email protected] Communicated by Lars R. Knudsen Received 20 July 2007 and revised 25 June 2009 Online publication 23 July 2009 Abstract. We describe several software side-channel attacks based on inter-process leakage through the state of the CPU’s memory cache. This leakage reveals memory access patterns, which can be used for cryptanalysis of cryptographic primitives that employ data-dependent table lookups. The attacks allow an unprivileged process to attack other processes running in parallel on the same processor, despite partitioning methods such as memory protection, sandboxing, and virtualization. Some of our meth- ods require only the ability to trigger services that perform encryption or MAC using the unknown key, such as encrypted disk partitions or secure network links. Moreover, we demonstrate an extremely strong type of attack, which requires knowledge of nei- ther the specific plaintexts nor ciphertexts and works by merely monitoring the effect of the cryptographic process on the cache. We discuss in detail several attacks on AES and experimentally demonstrate their applicability to real systems, such as OpenSSL and Linux’s dm-crypt encrypted partitions (in the latter case, the full key was recov- ered after just 800 writes to the partition, taking 65 milliseconds). -

E:\Ghcstop\AESOP Ghcstop Doc\Kernel\Ramdisk Howto\060405-Aesop2440-Ramdisk-Howto.Txt 200 06-04-06, 12:43:53오후 Aesop 2440 Kernel 2.6.13 Ramdisk Howto
파일: E:\ghcstop\AESOP_ghcstop_doc\kernel\ramdisk_howto\060405-aesop2440-ramdisk-howto.txt 200 06-04-06, 12:43:53오후 aesop 2440 kernel 2.6.13 ramdisk howto - 20060406(까먹고 민방위 못간날...^^) by godori 1. kernel설정을 다음과 같이 바꾼다. Device Drivers -> Block device쪽을 보시면.... Linux Kernel v2.6.13-h1940-aesop2440 Configuration qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq lqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq Block devices qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqk x Arrow keys navigate the menu. <Enter> selects submenus --->. x x Highlighted letters are hotkeys. Pressing <Y> includes, <N> excludes, x x <M> modularizes features. Press <Esc><Esc> to exit, <?> for Help, </> x x for Search. Legend: [*] built-in [ ] excluded <M> module < > module x x lqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqk x x x < > XT hard disk support x x x x <*> Loopback device support x x x x < > Cryptoloop Support x x x x <*> Network block device support x x x x < > Low Performance USB Block driver x x x x <*> RAM disk support x x x x (8) Default number of RAM disks x x x x (8192) Default RAM disk size (kbytes) x x x x [*] Initial RAM disk (initrd) support x x x x () Initramfs source file(s) x x x x < > Packet writing on CD/DVD media x x x x IO Schedulers ---> x x x x < > ATA over Ethernet support x x x x x x x x x x x x x x x x x x x mqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqj x tqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqu x <Select> < Exit > < Help > x mqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqj 여기서 8192 는 ramdisk size 입니다 . 만드는 ramdisk 크기에 맞게끔 바꿔주시고... File systems쪽에서 Linux Kernel v2.6.13-h1940-aesop2440 Configuration qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq lqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq File systems qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqk x Arrow keys navigate the menu. -
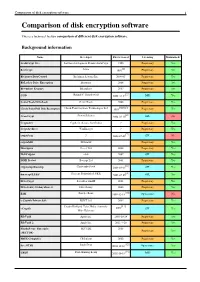
Comparison of Disk Encryption Software 1 Comparison of Disk Encryption Software
Comparison of disk encryption software 1 Comparison of disk encryption software This is a technical feature comparison of different disk encryption software. Background information Name Developer First released Licensing Maintained? ArchiCrypt Live Softwaredevelopment Remus ArchiCrypt 1998 Proprietary Yes [1] BestCrypt Jetico 1993 Proprietary Yes BitArmor DataControl BitArmor Systems Inc. 2008-05 Proprietary Yes BitLocker Drive Encryption Microsoft 2006 Proprietary Yes Bloombase Keyparc Bloombase 2007 Proprietary Yes [2] CGD Roland C. Dowdeswell 2002-10-04 BSD Yes CenterTools DriveLock CenterTools 2008 Proprietary Yes [3][4][5] Check Point Full Disk Encryption Check Point Software Technologies Ltd 1999 Proprietary Yes [6] CrossCrypt Steven Scherrer 2004-02-10 GPL No Cryptainer Cypherix (Secure-Soft India) ? Proprietary Yes CryptArchiver WinEncrypt ? Proprietary Yes [7] cryptoloop ? 2003-07-02 GPL No cryptoMill SEAhawk Proprietary Yes Discryptor Cosect Ltd. 2008 Proprietary Yes DiskCryptor ntldr 2007 GPL Yes DISK Protect Becrypt Ltd 2001 Proprietary Yes [8] cryptsetup/dmsetup Christophe Saout 2004-03-11 GPL Yes [9] dm-crypt/LUKS Clemens Fruhwirth (LUKS) 2005-02-05 GPL Yes DriveCrypt SecurStar GmbH 2001 Proprietary Yes DriveSentry GoAnywhere 2 DriveSentry 2008 Proprietary Yes [10] E4M Paul Le Roux 1998-12-18 Open source No e-Capsule Private Safe EISST Ltd. 2005 Proprietary Yes Dustin Kirkland, Tyler Hicks, (formerly [11] eCryptfs 2005 GPL Yes Mike Halcrow) FileVault Apple Inc. 2003-10-24 Proprietary Yes FileVault 2 Apple Inc. 2011-7-20 Proprietary -

Block Devices and Volume Management in Linux
Block devices and volume management in Linux Krzysztof Lichota [email protected] L i n u x b l o c k d e v i c e s l a y e r ● Linux block devices layer is pretty flexible and allows for some interesting features: – Pluggable I/O schedulers – I/O prioritizing (needs support from I/O scheduler) – Remapping of disk requests (Device Mapper) – RAID – Various tricks (multipath, fault injection) – I/O tracing (blktrace) s t r u c t b i o ● Basic block of I/O submission and completion ● Can represent large contiguous memory regions for I/O but also scattered regions ● Scattered regions can be passed directly to disks capable of scatter/gather ● bios can be split, merged with other requests by various levels of block layer (e.g. split by RAID, merged in disk driver with other disk requests) s t r u c t b i o f i e l d s ● bi_sector – start sector of I/O ● bi_size – size of I/O ● bi_bdev – device to which I/O is sent ● bi_flags – I/O flags ● bi_rw – read/write flags and priority ● bi_io_vec – memory scatter/gather vector ● bi_end_io - function called when I/O is completed ● bi_destructor – function called when bio is to be destroyed s t r u c t b i o u s a g e ● Allocate bio using bio_alloc() or similar function ● Fill in necessary fields (start, device, ...) ● Initialize bio vector ● Fill in end I/O function to be notified when bio completes ● Call submit_bio()/generic_make_request() ● Example: process_read() in dm-crypt O t h e r I / O s u b m i s s i o n f u n c t i o n s ● Older interfaces for submitting I/O are supported (but deprecated), -

Unbreakable Enterprise Kernel Release Notes for Unbreakable Enterprise Kernel Release 6 Update 1
Unbreakable Enterprise Kernel Release Notes for Unbreakable Enterprise Kernel Release 6 Update 1 F35561-04 May 2021 Oracle Legal Notices Copyright © 2020, 2021 Oracle and/or its affiliates. This software and related documentation are provided under a license agreement containing restrictions on use and disclosure and are protected by intellectual property laws. Except as expressly permitted in your license agreement or allowed by law, you may not use, copy, reproduce, translate, broadcast, modify, license, transmit, distribute, exhibit, perform, publish, or display any part, in any form, or by any means. Reverse engineering, disassembly, or decompilation of this software, unless required by law for interoperability, is prohibited. The information contained herein is subject to change without notice and is not warranted to be error-free. If you find any errors, please report them to us in writing. If this is software or related documentation that is delivered to the U.S. Government or anyone licensing it on behalf of the U.S. Government, then the following notice is applicable: U.S. GOVERNMENT END USERS: Oracle programs (including any operating system, integrated software, any programs embedded, installed or activated on delivered hardware, and modifications of such programs) and Oracle computer documentation or other Oracle data delivered to or accessed by U.S. Government end users are "commercial computer software" or "commercial computer software documentation" pursuant to the applicable Federal Acquisition Regulation and agency-specific supplemental regulations. As such, the use, reproduction, duplication, release, display, disclosure, modification, preparation of derivative works, and/or adaptation of i) Oracle programs (including any operating system, integrated software, any programs embedded, installed or activated on delivered hardware, and modifications of such programs), ii) Oracle computer documentation and/or iii) other Oracle data, is subject to the rights and limitations specified in the license contained in the applicable contract. -

Security Features for UBIFS
Security features for UBIFS Richard Weinberger sigma star gmbh . Richard Weinberger sigma star gmbh Security features for UBIFS /me ? Richard Weinberger ? Co-founder of sigma star gmbh ? Linux kernel developer and maintainer ? Strong focus on Linux kernel, lowlevel components, virtualization, security . Richard Weinberger sigma star gmbh Security features for UBIFS Disk Encryption on Linux ? Multiple existing solutions ? Kernel: dm-crypt, cryptoloop, eCryptFS, fscrypt ? Userspace: encFS, VeraCrypt, . Richard Weinberger sigma star gmbh Security features for UBIFS dm-crypt, cryptoloop ? Work on top of block devices ? Encrypt individual blocks ? Single key for every block ? Full file contents and metadata encryption ? Not suitable for MTD ? But stacking is possible: MTD, UBIFS, container file, dm-crypt/cryptoloop, block filesystem . Richard Weinberger sigma star gmbh Security features for UBIFS eCryptFS ? Stacked on top of your regular filesystem ? Works on filesystem-level (i.e. \sees" files) ? Individual key per file ? File contents and filename encryption ? Stacking filesystems can be problematic ? Also overhead in performance and memory ? Usable on MTD/UBIFS . Richard Weinberger sigma star gmbh Security features for UBIFS encFS, VeraCrypt, . ? Userspace filesystems ? Work on top of block devices ? Usually not what you want on (deeply) embedded systems . Richard Weinberger sigma star gmbh Security features for UBIFS fscrypt ? A better eCryptFS ? Fairly new, added for ext4 ? Encryption baked directly into filesystem (no stacking overhead) ? Intended to encrypt individual directories (e.g. home directory) ? Google use case: Android, ChromeOS . Richard Weinberger sigma star gmbh Security features for UBIFS Why no dm-crypt-like Solution for MTD? ? No individual key per inode ? On NAND, empty pages need special handling ? Stacking ? On a second thought it didn't feel right . -

Demands, Solutions, and Improvements for Linux Filesystem Security
Demands, Solutions, and Improvements for Linux Filesystem Security Michael Austin Halcrow International Business Machines, Inc. [email protected] Abstract 1 Development Efforts Securing file resources under Linux is a team This paper is motivated by an effort on the part effort. No one library, application, or kernel of the IBM Linux Technology Center to en- feature can stand alone in providing robust se- hance Linux filesystem security through bet- curity. Current Linux access control mecha- ter integration of encryption technology. The nisms work in concert to provide a certain level author of this paper is working together with of security, but they depend upon the integrity the external community and several members of the machine itself to protect that data. Once of the LTC in the design and development of the data leaves that machine, or if the machine a transparent cryptographic filesystem layer in itself is physically compromised, those access the Linux kernel. The “we” in this paper refers control mechanisms can no longer protect the to immediate members of the author’s devel- data in the filesystem. At that point, data pri- opment team who are working together on this vacy must be enforced via encryption. project, although many others outside that de- velopment team have thus far had a significant As Linux makes inroads in the desktop market, part in this development effort. the need for transparent and effective data en- cryption increases. To be practically deploy- able, the encryption/decryption process must 2 The Filesystem Security be secure, unobtrusive, consistent, flexible, re- liable, and efficient. Most encryption mecha- 2.1 Threat Model nisms that run under Linux today fail in one or more of these categories. -

Unbreakable Enterprise Kernel Release Notes for Unbreakable Enterprise Kernel Release 5 Update 4
Unbreakable Enterprise Kernel Release Notes for Unbreakable Enterprise Kernel Release 5 Update 4 F34758-08 May 2021 Oracle Legal Notices Copyright © 2020, 2021, Oracle and/or its affiliates. This software and related documentation are provided under a license agreement containing restrictions on use and disclosure and are protected by intellectual property laws. Except as expressly permitted in your license agreement or allowed by law, you may not use, copy, reproduce, translate, broadcast, modify, license, transmit, distribute, exhibit, perform, publish, or display any part, in any form, or by any means. Reverse engineering, disassembly, or decompilation of this software, unless required by law for interoperability, is prohibited. The information contained herein is subject to change without notice and is not warranted to be error-free. If you find any errors, please report them to us in writing. If this is software or related documentation that is delivered to the U.S. Government or anyone licensing it on behalf of the U.S. Government, then the following notice is applicable: U.S. GOVERNMENT END USERS: Oracle programs (including any operating system, integrated software, any programs embedded, installed or activated on delivered hardware, and modifications of such programs) and Oracle computer documentation or other Oracle data delivered to or accessed by U.S. Government end users are "commercial computer software" or "commercial computer software documentation" pursuant to the applicable Federal Acquisition Regulation and agency-specific supplemental regulations. As such, the use, reproduction, duplication, release, display, disclosure, modification, preparation of derivative works, and/or adaptation of i) Oracle programs (including any operating system, integrated software, any programs embedded, installed or activated on delivered hardware, and modifications of such programs), ii) Oracle computer documentation and/or iii) other Oracle data, is subject to the rights and limitations specified in the license contained in the applicable contract.