DOCSLIB.ORG

Bottom-Up Parsing Swarnendu Biswas

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bottom-Up Parsing Swarnendu Biswas CS 335: Bottom-up Parsing Swarnendu Biswas Semester 2019-2020-II CSE, IIT Kanpur Content influenced by many excellent references, see References slide for acknowledgements. Rightmost Derivation of 푎푏푏푐푑푒 푆 → 푎퐴퐵푒 Input string: 푎푏푏푐푑푒 퐴 → 퐴푏푐 | 푏 푆 → 푎퐴퐵푒 퐵 → 푑 → 푎퐴푑푒 → 푎퐴푏푐푑푒 → 푎푏푏푐푑푒 푆 푟푚 푆 푟푚 푆 푟푚 푆 푟푚 푆 푎 퐴 퐵 푒 푎 퐴 퐵 푒 푎 퐴 퐵 푒 푎 퐴 퐵 푒 푑 퐴 푏 푐 푑 퐴 푏 푐 푑 푏 CS 335 Swarnendu Biswas Bottom-up Parsing Constructs the parse tree starting from the leaves and working up toward the root 푆 → 푎퐴퐵푒 Input string: 푎푏푏푐푑푒 퐴 → 퐴푏푐 | 푏 푆 → 푎퐴퐵푒 푎푏푏푐푑푒 퐵 → 푑 → 푎퐴푑푒 → 푎퐴푏푐푑푒 → 푎퐴푏푐푑푒 → 푎퐴푑푒 → 푎푏푏푐푑푒 → 푎퐴퐵푒 → 푆 reverse of rightmost CS 335 Swarnendu Biswas derivation Bottom-up Parsing 푆 → 푎퐴퐵푒 Input string: 푎푏푏푐푑푒 퐴 → 퐴푏푐 | 푏 푎푏푏푐푑푒 퐵 → 푑 → 푎퐴푏푐푑푒 → 푎퐴푑푒 → 푎퐴퐵푒 → 푆 푎푏푏푐푑푒⇒ 푎 퐴 푏 푐 푑 푒 ⇒ 푎 퐴 푑 푒 ⇒ 푎 퐴 퐵 푒 ⇒ 푆 푏 퐴 푏 푐 퐴 푏 푐 푑 푎 퐴 퐵 푒 푏 푏 퐴 푏 푐 푑 푏 CS 335 Swarnendu Biswas Reduction • Bottom-up parsing reduces a string 푤 to the start symbol 푆 • At each reduction step, a chosen substring that is the rhs (or body) of a production is replaced by the lhs (or head) nonterminal Derivation 푆 훾0 훾1 훾2 … 훾푛−1 훾푛 = 푤 푟푚 푟푚 푟푚 푟푚 푟푚 푟푚 Bottom-up Parser CS 335 Swarnendu Biswas Handle • Handle is a substring that matches the body of a production • Reducing the handle is one step in the reverse of the rightmost derivation Right Sentential Form Handle Reducing Production 퐸 → 퐸 + 푇 | 푇 ∗ 퐹 → 푇 → 푇 ∗ 퐹 | 퐹 id1 id2 id1 id 퐹 → 퐸 | id 퐹 ∗ id2 퐹 푇 → 퐹 푇 ∗ id2 id2 퐹 → id 푇 ∗ 퐹 푇 ∗ 퐹 푇 → 푇 ∗ 퐹 푇 푇 퐸 → 푇 CS 335 Swarnendu Biswas Handle Although 푇 is the body of the production 퐸 → 푇, 푇 is not a handle in the sentential form 푇 ∗ id2 Right Sentential Form Handle Reducing Production 퐸 → 퐸 + 푇 | 푇 ∗ 퐹 → 푇 → 푇 ∗ 퐹 | 퐹 id1 id2 id1 id 퐹 → 퐸 | id 퐹 ∗ id2 퐹 푇 → 퐹 푇 ∗ id2 id2 퐹 → id 푇 ∗ 퐹 푇 ∗ 퐹 푇 → 푇 ∗ 퐹 푇 푇 퐸 → 푇 CS 335 Swarnendu Biswas Handle • If 푆 ∗ 훼퐴푤 훼훽푤, then 퐴 → 푟푚 푟푚 푆 훽 is a handle of 훼훽푤 • String 푤 right of a handle must 퐴 contain only terminals 훼 훽 푤 A handle 퐴 → 훽 in the parse tree for 훼훽푤 CS 335 Swarnendu Biswas Handle If grammar 퐺 is unambiguous, then every right sentential form has only one handle If 퐺 is ambiguous, then there can be more than one rightmost derivation of 훼훽푤 CS 335 Swarnendu Biswas Shift-Reduce Parsing CS 335 Swarnendu Biswas Shift-Reduce Parsing • Type of bottom-up parsing with two primary actions, shift and reduce • Other obvious actions are accept and error • The input string (i.e., being parsed) consists of two parts • Left part is a string of terminals and nonterminals, and is stored in stack • Right part is a string of terminals read from an input buffer • Bottom of the stack and end of input are represented by $ CS 335 Swarnendu Biswas Shift-Reduce Actions • Shift: shift the next input symbol from the right string onto the top of the stack • Reduce: identify a string on top of the stack that is the body of a production, and replace the body with the head CS 335 Swarnendu Biswas Shift-Reduce Parsing • Initial Stack Input $ 푤$ ⇒ Shift ∗ Reduce • Final goal Stack Input $푆 $ CS 335 Swarnendu Biswas 퐸 → 퐸 + 푇 | 푇 Shift-Reduce Parsing 푇 → 푇 ∗ 퐹 | 퐹 퐹 → 퐸 | id Stack Input Action $ 퐢퐝1 ∗ 퐢퐝2$ Shift $퐢퐝1 ∗ 퐢퐝2$ Reduce by 퐹 → id $퐹 ∗ 퐢퐝2$ Reduce by 푇 → 퐹 $푇 ∗ 퐢퐝2$ Shift $푇 ∗ 퐢퐝2$ Shift $푇 ∗ 퐢퐝2 $ Reduce by 퐹 → id $푇 ∗ 퐹 $ Reduce by 푇 → 푇 ∗ 퐹 $푇 $ Reduce by 퐸 → 푇 $퐸 $ Accept CS 335 Swarnendu Biswas Handle on Top of the Stack • Is the following scenario possible? Stack Input Action … $ 훼훽훾 푤$ Reduce by 퐴 → 훾 $ 훼훽퐴 푤$ Reduce by 퐵 → 훽 $훼퐵퐴 푤$ … CS 335 Swarnendu Biswas Possible Choices in Rightmost Derivation 1. 푆 훼퐴푧 훼훽퐵푦푧 훼훽훾푦푧 2. 푆 훼퐵푥퐴푧 훼퐵푥푦푧 훼훾푥푦푧 푟푚 푟푚 푟푚 푟푚 푟푚 푟푚 푆 푆 퐴 퐵 퐴 퐵 훼 훾 푥 푦 푧 훼 훽 훾 푦 푧 CS 335 Swarnendu Biswas Handle on Top of the Stack • Is the following scenario possible? Stack Input Action … $ 훼훽훾 푤$ Reduce by 퐴 → 훾 Handle$ 훼훽퐴 always eventually appears on top of푤$ theReduce stack, by 퐵 never→ 훽 inside $훼퐵퐴 푤$ … CS 335 Swarnendu Biswas Shift-Reduce Actions • Shift: shift the next input symbol from the right string onto the top of the stack • Reduce: identify a string on top of the stack that is the body of a production, and replace the body with the head How do you decide when to shift and when to reduce? CS 335 Swarnendu Biswas Steps in Shift-Reduce Parsers General shift-reduce technique If there is no handle on the stack, then shift If there is a handle on the stack, then reduce • Bottom up parsing is essentially the process of detecting handles and reducing them • Different bottom-up parsers differ in the way they detect handles CS 335 Swarnendu Biswas Challenges in Bottom-up Parsing Which action do you •Both shift and reduce are valid, pick when there is a choice? implies a shift-reduce conflict Which rule to use if reduction is possible by more than one •Reduce-reduce conflict rule? CS 335 Swarnendu Biswas Shift-Reduce Conflict 퐸 → 퐸 + 퐸 퐸 ∗ 퐸 id id + id ∗ id id + id ∗ id Stack Input Action Stack Input Action $ id + id ∗ id$ Shift $ id + id ∗ id$ Shift … … $퐸 + 퐸 ∗ id$ Reduce by 퐸 → 퐸 + 퐸 $퐸 + 퐸 ∗ id$ Shift $퐸 ∗ id$ Shift $퐸 + 퐸 ∗ id$ Shift $퐸 ∗ id$ Shift $퐸 + 퐸 ∗ id $ Reduce by 퐸 → id $퐸 ∗ id $ Reduce by 퐸 → id $퐸 + 퐸 ∗ 퐸 $ Reduce by 퐸 → 퐸 ∗ 퐸 $퐸 ∗ 퐸 $ Reduce by 퐸 → 퐸 ∗ 퐸 $퐸 + 퐸 $ Reduce by 퐸 → 퐸 + 퐸 $퐸 $ $퐸 $ CS 335 Swarnendu Biswas Shift-Reduce Conflict S푡푚푡 → if 퐸푥푝푟 then 푆푡푚푡 | if 퐸푥푝푟 then 푆푡푚푡 else 푆푡푚푡 | 표푡ℎ푒푟 Stack Input Action … if 퐸푥푝푟 then 푆푡푚푡 else … $ CS 335 Swarnendu Biswas Shift-Reduce Conflict S푡푚푡 → if 퐸푥푝푟 then 푆푡푚푡 | if 퐸푥푝푟 then 푆푡푚푡 else 푆푡푚푡 | 표푡ℎ푒푟 Stack Input Action … if 퐸푥푝푟 then 푆푡푚푡 else … $ What is a correct thing to do for this grammar – shift or reduce? CS 335 Swarnendu Biswas 푀 → 푅 + 푅 푅 + 푐 푅 Reduce-Reduce Conflict 푅 → 푐 푐 + 푐 푐 + 푐 Stack Input Action Stack Input Action $ 푐 + 푐$ Shift $ 푐 + 푐$ Shift $푐 +푐$ Reduce by 푅 → 푐 $푐 +푐$ Reduce by 푅 → 푐 $푅 +푐$ Shift $푅 +푐$ Shift $푅 + 푐$ Shift $푅 + 푐$ Shift $푅 + 푐 $ Reduce by 푅 → 푐 $푅 + 푐 $ Reduce by 푀 → 푅 + 푐 $푅 + 푅 $ Reduce by 푅 → 푅 + 푅 $푀 $ $푀 $ CS 335 Swarnendu Biswas LR Parsing CS 335 Swarnendu Biswas LR(k) Parsing • Popular bottom-up parsing scheme • L is for left-to-right scan of input • R is for reverse of rightmost derivation • k is the number of lookahead symbols • LR parsers are table-driven, like the nonrecursive LL parser • LR grammar is one for which we can construct an LR parsing table CS 335 Swarnendu Biswas Popularity of LR Parsing Can recognize all language constructs with CFGs Most general nonbacktracking shift-reduce parsing method Works for a superset of grammars parsed with predictive or LL parsers Why? CS 335 Swarnendu Biswas Popularity of LR Parsing Can recognize all language constructs with CFGs Most general nonbacktracking shift-reduce parsing method Works for a superset of grammars parsed with predictive or LL parsers • LL(k) parsing predicts which production to use having seen only the first k tokens of the right-hand side • LR(k) parsing can decide after it has seen input tokens corresponding to the entire right-hand side of the production CS 335 Swarnendu Biswas Block Diagram of LR Parser Input 푎1 … … 푎푖 … … 푎푛 $ LR Parsing Stack 푠푚 Output Program 푠푚−1 … ACTION GOTO $ Parse Table CS 335 Swarnendu Biswas LR Parsing • Remember the basic question: when to shift and when to reduce! • Information is encoded in a DFA constructed using canonical LR(0) collection I. Augmented grammar 퐺′ with new start symbol 푆′ and rule 푆′ → 푆 II. Define helper functions Closure() and Goto() CS 335 Swarnendu Biswas LR(0) Item • An LR(0) item (also called item) Production Items of a grammar 퐺 is a production of 퐺 with a dot at some position 퐴 → •푋푌푍 in the body 퐴 → 푋•푌푍 퐴 → 푋푌푍 퐴 → 푋푌•푍 • An item indicates how much of a production we have seen 퐴 → 푋푌푍• • Symbols on the left of “•” are already on the stack 퐴 → •푋푌푍 indicates that we expect a • Symbols on the right of “•” are string derivable from 푋푌푍 next on expected in the input the input CS 335 Swarnendu Biswas Closure Operation • Let 퐼 be a set of items for a grammar 퐺 • Closure(퐼) is constructed by 1. Add every item in 퐼 to Closure(퐼) 2. If 퐴 → 훼•퐵훽 is in Closure(퐼) and 퐵 → 훾 is a rule, then add 퐵 → 훾 to Closure(퐼) if not already added 3. Repeat until no more new items can be added to Closure(퐼) CS 335 Swarnendu Biswas Example of Closure Suppose 퐼 = {퐸′ → •퐸 }, compute 퐸′ → 퐸 퐸 → 퐸 + 푇 | 푇 Closure(퐼) 푇 → 푇 ∗ 퐹 | 퐹 퐹 → 퐸 | id CS 335 Swarnendu Biswas Example of Closure Suppose 퐼 = {퐸′ → •퐸 } 퐸′ → 퐸 퐸 → 퐸 + 푇 | 푇 Closure(퐼) = { 푇 → 푇 ∗ 퐹 | 퐹 퐸′ → •퐸, 퐹 → 퐸 | id 퐸 → •퐸 + 푇, 퐸 → •푇, 푇 → •푇 ∗ 퐹, 푇 → •퐹, 퐹 → • 퐸 , 퐹 → •id } CS 335 Swarnendu Biswas Kernel and Nonkernel Items • If one 퐵-production is added to Closure(퐼) with the dot at the left end, then all 퐵-productions will be added to the closure • Kernel items • Initial item 푆′ → •푆, and all items whose dots are not at the left end • Nonkernel items • All items with their dots at the left end, except for 푆′ → •푆 CS 335 Swarnendu Biswas Goto Operation • Suppose 퐼 is a set of items and 푋 is a grammar symbol • Goto(퐼, 푋) is the closure of set all items [퐴 → 훼푋•훽] such that [퐴 → 훼•푋훽] is in 퐼 • If 퐼 is a set of items for some valid prefix 훼, then Goto(퐼,푋) is set of valid items for prefix 훼푋 • Intuitively, Goto(퐼, 푋) defines the transitions in the LR(0) automaton • Goto(퐼, 푋) gives the transition from state 퐼 under input 푋 CS 335 Swarnendu Biswas Example of Goto • Compute Goto(퐼, +) 퐸′ → 퐸 퐸 → 퐸 + 푇 | 푇 푇 → 푇 ∗ 퐹 | 퐹 퐹 → 퐸 | id Suppose 퐼 = { 퐸′ → 퐸•, 퐸 → 퐸• + 푇 } CS 335 Swarnendu Biswas Example of Goto Goto(퐼, +) = { 퐸′ → 퐸 퐸 → 퐸 + 푇 | 푇 퐸 → 퐸 + •푇, 푇 → 푇 ∗ 퐹 | 퐹 푇 → •푇 ∗ 퐹, 퐹 → 퐸 | id 푇 → •퐹, 퐹 → • 퐸 , Suppose 퐼 = { 퐹 → •id 퐸′ → 퐸•, } 퐸 → 퐸• + 푇 } CS 335
Load more

Recommended publications
  • Parser Tables for Non-LR(1) Grammars with Conflict Resolution Joel E
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Science of Computer Programming 75 (2010) 943–979 Contents lists available at ScienceDirect Science of Computer Programming journal homepage: www.elsevier.com/locate/scico The IELR(1) algorithm for generating minimal LR(1) parser tables for non-LR(1) grammars with conflict resolution Joel E. Denny ∗, Brian A. Malloy School of Computing, Clemson University, Clemson, SC 29634, USA article info a b s t r a c t Article history: There has been a recent effort in the literature to reconsider grammar-dependent software Received 17 July 2008 development from an engineering point of view. As part of that effort, we examine a Received in revised form 31 March 2009 deficiency in the state of the art of practical LR parser table generation. Specifically, LALR Accepted 12 August 2009 sometimes generates parser tables that do not accept the full language that the grammar Available online 10 September 2009 developer expects, but canonical LR is too inefficient to be practical particularly during grammar development. In response, many researchers have attempted to develop minimal Keywords: LR parser table generation algorithms. In this paper, we demonstrate that a well known Grammarware Canonical LR algorithm described by David Pager and implemented in Menhir, the most robust minimal LALR LR(1) implementation we have discovered, does not always achieve the full power of Minimal LR canonical LR(1) when the given grammar is non-LR(1) coupled with a specification for Yacc resolving conflicts. We also detail an original minimal LR(1) algorithm, IELR(1) (Inadequacy Bison Elimination LR(1)), which we have implemented as an extension of GNU Bison and which does not exhibit this deficiency.
    [Show full text]
  • Chapter 4 Syntax Analysis
    Chapter 4 Syntax Analysis By Varun Arora Outline Role of parser Context free grammars Top down parsing Bottom up parsing Parser generators By Varun Arora The role of parser token Source Lexical Parse tree Rest of Intermediate Parser program Analyzer Front End representation getNext Token Symbol table By Varun Arora Uses of grammars E -> E + T | T T -> T * F | F F -> (E) | id E -> TE’ E’ -> +TE’ | Ɛ T -> FT’ T’ -> *FT’ | Ɛ F -> (E) | id By Varun Arora Error handling Common programming errors Lexical errors Syntactic errors Semantic errors Lexical errors Error handler goals Report the presence of errors clearly and accurately Recover from each error quickly enough to detect subsequent errors Add minimal overhead to the processing of correct progrms By Varun Arora Error-recover strategies Panic mode recovery Discard input symbol one at a time until one of designated set of synchronization tokens is found Phrase level recovery Replacing a prefix of remaining input by some string that allows the parser to continue Error productions Augment the grammar with productions that generate the erroneous constructs Global correction Choosing minimal sequence of changes to obtain a globally least-cost correction By Varun Arora Context free grammars Terminals Nonterminals expression -> expression + term Start symbol expression -> expression – term productions expression -> term term -> term * factor term -> term / factor term -> factor factor -> (expression) factor -> id By Varun Arora Derivations Productions are treated as
    [Show full text]
  • Validating LR(1) Parsers
    Validating LR(1) Parsers Jacques-Henri Jourdan1;2, Fran¸coisPottier2, and Xavier Leroy2 1 Ecole´ Normale Sup´erieure 2 INRIA Paris-Rocquencourt Abstract. An LR(1) parser is a finite-state automaton, equipped with a stack, which uses a combination of its current state and one lookahead symbol in order to determine which action to perform next. We present a validator which, when applied to a context-free grammar G and an automaton A, checks that A and G agree. Validating the parser pro- vides the correctness guarantees required by verified compilers and other high-assurance software that involves parsing. The validation process is independent of which technique was used to construct A. The validator is implemented and proved correct using the Coq proof assistant. As an application, we build a formally-verified parser for the C99 language. 1 Introduction Parsing remains an essential component of compilers and other programs that input textual representations of structured data. Its theoretical foundations are well understood today, and mature technology, ranging from parser combinator libraries to sophisticated parser generators, is readily available to help imple- menting parsers. The issue we focus on in this paper is that of parser correctness: how to obtain formal evidence that a parser is correct with respect to its specification? Here, following established practice, we choose to specify parsers via context-free grammars enriched with semantic actions. One application area where the parser correctness issue naturally arises is formally-verified compilers such as the CompCert verified C compiler [14]. In- deed, in the current state of CompCert, the passes that have been formally ver- ified start at abstract syntax trees (AST) for the CompCert C subset of C and extend to ASTs for three assembly languages.
    [Show full text]
  • CLR(1) and LALR(1) Parsers
    CLR(1) and LALR(1) Parsers C.Naga Raju B.Tech(CSE),M.Tech(CSE),PhD(CSE),MIEEE,MCSI,MISTE Professor Department of CSE YSR Engineering College of YVU Proddatur 6/21/2020 Prof.C.NagaRaju YSREC of YVU 9949218570 Contents • Limitations of SLR(1) Parser • Introduction to CLR(1) Parser • Animated example • Limitation of CLR(1) • LALR(1) Parser Animated example • GATE Problems and Solutions Prof.C.NagaRaju YSREC of YVU 9949218570 Drawbacks of SLR(1) ❖ The SLR Parser discussed in the earlier class has certain flaws. ❖ 1.On single input, State may be included a Final Item and a Non- Final Item. This may result in a Shift-Reduce Conflict . ❖ 2.A State may be included Two Different Final Items. This might result in a Reduce-Reduce Conflict Prof.C.NagaRaju YSREC of YVU 6/21/2020 9949218570 ❖ 3.SLR(1) Parser reduces only when the next token is in Follow of the left-hand side of the production. ❖ 4.SLR(1) can reduce shift-reduce conflicts but not reduce-reduce conflicts ❖ These two conflicts are reduced by CLR(1) Parser by keeping track of lookahead information in the states of the parser. ❖ This is also called as LR(1) grammar Prof.C.NagaRaju YSREC of YVU 6/21/2020 9949218570 CLR(1) Parser ❖ LR(1) Parser greatly increases the strength of the parser, but also the size of its parse tables. ❖ The LR(1) techniques does not rely on FOLLOW sets, but it keeps the Specific Look-ahead with each item. Prof.C.NagaRaju YSREC of YVU 6/21/2020 9949218570 CLR(1) Parser ❖ LR(1) Parsing configurations have the general form: A –> X1...Xi • Xi+1...Xj , a ❖ The Look Ahead
    [Show full text]
  • Parser Generation Bottom-Up Parsing LR Parsing Constructing LR Parser
    CS421 COMPILERS AND INTERPRETERS CS421 COMPILERS AND INTERPRETERS Parser Generation Bottom-Up Parsing • Main Problem: given a grammar G, how to build a top-down parser or a • Construct parse tree “bottom-up” --- from leaves to the root bottom-up parser for it ? • Bottom-up parsing always constructs right-most derivation • parser : a program that, given a sentence, reconstructs a derivation for that • Important parsing algorithms: shift-reduce, LR parsing sentence ---- if done sucessfully, it “recognize” the sentence • LR parser components: input, stack (strings of grammar symbols and states), • all parsers read their input left-to-right, but construct parse tree differently. driver routine, parsing tables. • bottom-up parsers --- construct the tree from leaves to root input: a1 a2 a3 a4 ...... an $ shift-reduce, LR, SLR, LALR, operator precedence stack s m LR Parsing output • top-down parsers --- construct the tree from root to leaves Xm .. recursive descent, predictive parsing, LL(1) s1 X1 s0 parsing Copyright 1994 - 2015 Zhong Shao, Yale University Parser Generation: Page 1 of 27 Copyright 1994 - 2015 Zhong Shao, Yale University Parser Generation: Page 2 of 27 CS421 COMPILERS AND INTERPRETERS CS421 COMPILERS AND INTERPRETERS LR Parsing Constructing LR Parser How to construct the parsing table and ? • A sequence of new state symbols s0,s1,s2,..., sm ----- each state ACTION GOTO sumarize the information contained in the stack below it. • basic idea: first construct DFA to recognize handles, then use DFA to construct the parsing tables ! different parsing table yield different LR parsers SLR(1), • Parsing configurations: (stack, remaining input) written as LR(1), or LALR(1) (s0X1s1X2s2...Xmsm , aiai+1ai+2...an$) • augmented grammar for context-free grammar G = G(T,N,P,S) is defined as G’ next “move” is determined by sm and ai = G’(T, N { S’}, P { S’ -> S}, S’) ------ adding non-terminal S’ and the • Parsing tables: ACTION[s,a] and GOTO[s,X] production S’ -> S, and S’ is the new start symbol.
    [Show full text]
  • Elkhound: a Fast, Practical GLR Parser Generator
    Published in Proc. of Conference on Compiler Construction, 2004, pp. 73–88. Elkhound: A Fast, Practical GLR Parser Generator Scott McPeak and George C. Necula ? University of California, Berkeley {smcpeak,necula}@cs.berkeley.edu Abstract. The Generalized LR (GLR) parsing algorithm is attractive for use in parsing programming languages because it is asymptotically efficient for typical grammars, and can parse with any context-free gram- mar, including ambiguous grammars. However, adoption of GLR has been slowed by high constant-factor overheads and the lack of a general, user-defined action interface. In this paper we present algorithmic and implementation enhancements to GLR to solve these problems. First, we present a hybrid algorithm that chooses between GLR and ordinary LR on a token-by-token ba- sis, thus achieving competitive performance for determinstic input frag- ments. Second, we describe a design for an action interface and a new worklist algorithm that can guarantee bottom-up execution of actions for acyclic grammars. These ideas are implemented in the Elkhound GLR parser generator. To demonstrate the effectiveness of these techniques, we describe our ex- perience using Elkhound to write a parser for C++, a language notorious for being difficult to parse. Our C++ parser is small (3500 lines), efficient and maintainable, employing a range of disambiguation strategies. 1 Introduction The state of the practice in automated parsing has changed little since the intro- duction of YACC (Yet Another Compiler-Compiler), an LALR(1) parser genera- tor, in 1975 [1]. An LALR(1) parser is deterministic: at every point in the input, it must be able to decide which grammar rule to use, if any, utilizing only one token of lookahead [2].
    [Show full text]
  • LR Parsing, LALR Parser Generators Lecture 10 Outline • Review Of
    Outline • Review of bottom-up parsing LR Parsing, LALR Parser Generators • Computing the parsing DFA • Using parser generators Lecture 10 Prof. Fateman CS 164 Lecture 10 1 Prof. Fateman CS 164 Lecture 10 2 Bottom-up Parsing (Review) The Shift and Reduce Actions (Review) • A bottom-up parser rewrites the input string • Recall the CFG: E → int | E + (E) to the start symbol • A bottom-up parser uses two kinds of actions: • The state of the parser is described as •Shiftpushes a terminal from input on the stack α I γ – α is a stack of terminals and non-terminals E + (I int ) ⇒ E + (int I ) – γ is the string of terminals not yet examined •Reducepops 0 or more symbols off the stack (the rule’s rhs) and pushes a non-terminal on • Initially: I x1x2 . xn the stack (the rule’s lhs) E + (E + ( E ) I ) ⇒ E +(E I ) Prof. Fateman CS 164 Lecture 10 3 Prof. Fateman CS 164 Lecture 10 4 LR(1) Parsing. An Example Key Issue: When to Shift or Reduce? int int + (int) + (int)$ shift 0 1 I int + (int) + (int)$ E → int • Idea: use a finite automaton (DFA) to decide E E → int I ( on $, + E I + (int) + (int)$ shift(x3) when to shift or reduce 2 + 3 4 E + (int I ) + (int)$ E → int – The input is the stack accept E int E + (E ) + (int)$ shift – The language consists of terminals and non-terminals on $ I ) E → int E + (E) I + (int)$ E → E+(E) 7 6 5 on ), + E I + (int)$ shift (x3) • We run the DFA on the stack and we examine E → E + (E) + E + (int )$ E → int the resulting state X and the token tok after I on $, + int I E + (E )$ shift –If X has a transition labeled tok then shift ( I 8 9 β E + (E) I $ E → E+(E) –If X is labeled with “A → on tok”then reduce E + E I $ accept 10 11 E → E + (E) Prof.
    [Show full text]
  • Unit-5 Parsers
    UNIT-5 PARSERS LR Parsers: • The most powerful shift-reduce parsing (yet efficient) is: • LR parsing is attractive because: – LR parsing is most general non-backtracking shift-reduce parsing, yet it is still efficient. – The class of grammars that can be parsed using LR methods is a proper superset of the class of grammars that can be parsed with predictive parsers. LL(1)-Grammars ⊂ LR(1)-Grammars – An LR-parser can detect a syntactic error as soon as it is possible to do so a left-to-right scan of the input. – covers wide range of grammars. • SLR – simple LR parser • LR – most general LR parser • LALR – intermediate LR parser (look-head LR parser) • SLR, LR and LALR work same (they used the same algorithm), only their parsing tables are different. LR Parsing Algorithm: A Configuration of LR Parsing Algorithm: A configuration of a LR parsing is: • Sm and ai decides the parser action by consulting the parsing action table. (Initial Stack contains just So ) • A configuration of a LR parsing represents the right sentential form: X1 ... Xm ai ai+1 ... an $ Actions of A LR-Parser: 1. shift s -- shifts the next input symbol and the state s onto the stack ( So X1 S1 ... Xm Sm, ai ai+1 ... an $ ) è ( So X1 S1 ..Xm Sm ai s, ai+1 ...an $ ) 2. reduce Aβ→ (or rn where n is a production number) – pop 2|β| (=r) items from the stack; – then push A and s where s=goto[sm-r,A] ( So X1 S1 ... Xm Sm, ai ai+1 ..
    [Show full text]
  • Compiler Construction
    Compiler construction PDF generated using the open source mwlib toolkit. See http://code.pediapress.com/ for more information. PDF generated at: Sat, 10 Dec 2011 02:23:02 UTC Contents Articles Introduction 1 Compiler construction 1 Compiler 2 Interpreter 10 History of compiler writing 14 Lexical analysis 22 Lexical analysis 22 Regular expression 26 Regular expression examples 37 Finite-state machine 41 Preprocessor 51 Syntactic analysis 54 Parsing 54 Lookahead 58 Symbol table 61 Abstract syntax 63 Abstract syntax tree 64 Context-free grammar 65 Terminal and nonterminal symbols 77 Left recursion 79 Backus–Naur Form 83 Extended Backus–Naur Form 86 TBNF 91 Top-down parsing 91 Recursive descent parser 93 Tail recursive parser 98 Parsing expression grammar 100 LL parser 106 LR parser 114 Parsing table 123 Simple LR parser 125 Canonical LR parser 127 GLR parser 129 LALR parser 130 Recursive ascent parser 133 Parser combinator 140 Bottom-up parsing 143 Chomsky normal form 148 CYK algorithm 150 Simple precedence grammar 153 Simple precedence parser 154 Operator-precedence grammar 156 Operator-precedence parser 159 Shunting-yard algorithm 163 Chart parser 173 Earley parser 174 The lexer hack 178 Scannerless parsing 180 Semantic analysis 182 Attribute grammar 182 L-attributed grammar 184 LR-attributed grammar 185 S-attributed grammar 185 ECLR-attributed grammar 186 Intermediate language 186 Control flow graph 188 Basic block 190 Call graph 192 Data-flow analysis 195 Use-define chain 201 Live variable analysis 204 Reaching definition 206 Three address
    [Show full text]
  • Pondicherry Engineering College Puducherry – 605 014
    1 PONDICHERRY ENGINEERING COLLEGE PUDUCHERRY – 605 014 Bachelor of Technology B.Tech., INFORMATION TECHNOLOGY Regulations, Curriculum & Syllabus Effective from the academic year 2013-2014 of PONDICHERRY UNIVERSITY PUDUCHERRY – 605 014. 2 PONDICHERRY UNIVERSITY BACHELOR OF TECHNOLOGY PROGRAMMES (EIGHT SEMESTERS) REGULATIONS 1. Conditions for Admission: (a ) Candidates for admission to the first semester of the 8 semester B.Tech Degree programme should be required to have passed : The Higher Secondary Examination of the (10+2) curriculum (Academic Stream) prescribed by the Government of Tamil Nadu or any other examination equivalent there to with minimum of 45% marks (40% marks for OBC and SC/ST candidates) in aggregate of subjects – Mathematics, Physics and any one of the following optional subjects: Chemistry / Biotechnology/ Computer Science / Biology (Botany & Zoology) or an Examination of any University or Authority recognized by the Executive Council of the Pondicherry University as equivalent thereto. (b) For Lateral entry in to third semester of the eight semester B.Tech programme : The minimum qualification for admission is a pass in three year diploma or four year sandwich diploma course in engineering / technology with a minimum of 45% marks ( 40% marks for OBC and SC/ST candidates) in aggregate in the subjects covered from 3 rd to final semester or a pass in any B.Sc. course with mathematics as one of the subjects of study in XII standard with a minimum of 45% marks ( 40% marks for OBC and a mere pass for SC/ST candidates) in aggregate in main and ancillary subjects excluding language subjects. The list of diploma programs approved for admission for each of the degree programs is given in Annexure A .
    [Show full text]
  • Practical Dynamic Grammars for Dynamic Languages Lukas Renggli, St´Ephane Ducasse, Tudor Gˆırba,Oscar Nierstrasz
    CORE Metadata, citation and similar papers at core.ac.uk Provided by HAL - Lille 3 Practical Dynamic Grammars for Dynamic Languages Lukas Renggli, St´ephane Ducasse, Tudor G^ırba,Oscar Nierstrasz To cite this version: Lukas Renggli, St´ephaneDucasse, Tudor G^ırba,Oscar Nierstrasz. Practical Dynamic Gram- mars for Dynamic Languages. 4th Workshop on Dynamic Languages and Applications (DYLA 2010), 2010, Malaga, Spain. 2010. <hal-00746253> HAL Id: hal-00746253 https://hal.inria.fr/hal-00746253 Submitted on 28 Oct 2012 HAL is a multi-disciplinary open access L'archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destin´eeau d´ep^otet `ala diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publi´esou non, lished or not. The documents may come from ´emanant des ´etablissements d'enseignement et de teaching and research institutions in France or recherche fran¸caisou ´etrangers,des laboratoires abroad, or from public or private research centers. publics ou priv´es. ∗ Practical Dynamic Grammars for Dynamic Languages Lukas Renggli Stéphane Ducasse Software Composition Group, RMoD, INRIA-Lille Nord University of Bern, Switzerland Europe, France scg.unibe.ch rmod.lille.inria.fr Tudor Gîrba Oscar Nierstrasz Sw-eng. Software Engineering Software Composition Group, GmbH, Switzerland University of Bern, Switzerland www.sw-eng.ch scg.unibe.ch ABSTRACT tion 2 introduces the PetitParser framework. Section 3 dis- Grammars for programming languages are traditionally spec- cusses important aspects of a dynamic approach, such as ified statically. They are hard to compose and reuse due composition, correctness, performance and tool support.
    [Show full text]
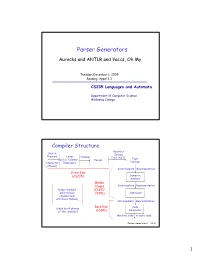
  • Parser Generators
    Parser Generators Aurochs and ANTLR and Yaccs,,y Oh My Tuesday, December 1, 2009 Reading: Appel 3.3 CS235 Languages and Automata Department of Computer Science Wellesley College Compiler Structure Abstract Source Syntax Program Lexer Tokens Tree (AST) Type (a.k.a. Scanner, Parser (character Tokenizer) Checker stream) Intermediate Representation Front End (CS235) Semantic Analysis Middle Stages Intermediate Representation Global Analysis (CS251/ Information CS301) Optimizer (Symbol and Attribute Tables) Intermediate Representation Back End Code (used by all phases Generator of the compiler) (CS301) Machine code or byte code Parser Generators 34-2 1 Motivation We now know how to construct LL(k) and LR(k) parsers by hand. But constructing parser tables from grammars and implementing parsers from parser tables is tedious and error prone. Isn’t there a better way? Idea: Hey, aren’t computers good at automating these sorts of things? Parser Generators 34-3 Parser Generators A parser generator is a program whose inputs are: 1. a grammar that specifies a tree structure for linear sequences of tokens (typically created by a separate lexer program). 2. a specification of semantic actions to perform when building the parse tree. Its output is an automatically constructed program that parses a token sequence into a tree, performing the specified semantic actions along the way In the remainder of this lecture, we will explore and compare a two parser generators: Yacc and Aurochs. Parser Generators 34-4 2 ml-yacc: An LALR(1) Parser Generator Slip.yacc
    [Show full text]