DOCSLIB.ORG

A Bio-Economic Model of Long-Run Striga Control with an Application to Subsistence Farming in Mali

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Bio-Economic Model of Long-Run Striga Control with an Application to Subsistence Farming in Mali A Bio-Economic Model of Long-Run Striga Control with an Application to Subsistence Farming in Mali Jeffrey D. Mullen Dissertation submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Agricultural and Applied Economics Daniel B. Taylor, Chair George W. Norton Jeffrey Alwang Bradford Mills John Caldwell February 18, 1999 Blacksburg, Virginia Keywords: Striga, Integrated Pest Management, Mali, Subsistence Farming, Dynamic Programming Copyright 1999, Jeffrey D. Mullen A Bio-Economic Model of Long-Run Striga Control with an Application to Subsistence Farming in Mali Jeffrey D. Mullen (ABSTRACT) The parasitic weeds belonging to the genus Striga are among the world’s most tenacious, prolific and destructive agricultural pests. Crop loss estimates due to Striga infestations can reach 100 percent. Furthermore, the weeds’ affinity for low-fertility soils and low rainfall means that those farming the most marginal lands are most severely affected. Nonetheless, subsistence farmer have yet to adopt seemingly beneficial control practices to any appreciable degree. This paper develops a bio-economic model capable of identifying: (1) affordable, effective Striga control practices consistent with the resource constraints of subsistence farmers; and (2) barriers to the adoption of those practices. The model is comprised of two components: a biological component modeling Striga population dynamics, and an economic component representing the production opportunity set, resource constraints, and price parameters farmers face. The model is applied to two zones in Northwestern Mali, Sirakorola and Mourdiah, and solved using non-linear, dynamic programming. Data collected by the USAID IPM- CRSP/Mali project are used to specify the economic parameters of the model. A new technique for estimating the lower bound of a farmer’s production planning horizon is also developed and employed in the application of the model to Sirakorola and Mourdiah. The results of several model scenarios indicate that the availability of information regarding the efficacy of Striga control practices is a primary barrier to their adoption by subsistence farmers. The movement of Striga seed between fields, however, is of limited importance. The “optimal control practices” identified by the model depend on the size and demographic composition of the production unit (UP), the zone in which the UP is located, and the cash budget available to the UP. At low budget levels, the model suggests planting millet without fertilizer at a high density in Sirakorola and a low density in Mourdiah. At high budget levels, the model suggests planting millet at a high density in both zones while applying urea. The benefits of adopting the optimal set of practices are presented in both nutritional and financial terms, and can reach as much as a ten-fold increase in the nutritional content of and financial returns to a harvest. iii Acknowledgements I would like to thank the United States Agency for International Development (USAID) for its generous support of this project through the Integrated Pest Management Collaborative Research Support Program (IPM-CRSP). I would also like to thank Mali’s Institute d’Economie Rurale for its logistical support in collecting primary data, as well as the considerable intellectual contributions of its staff, including Amadou Diarra, Madame Gambi, Bourema Dembele, Makan Fofana, and countless others. In addition, my thanks go to the Office of International Research and Development at Virginia Tech and its Director, S. K. DeDada, for the valuable administrative support offered during the course of this study. I would also like to recognize the contributions of my advisory committee. Drs. George Norton, Jeffrey Alwang, and Bradford Mills kept me focused on the larger economic issues related to the project. Dr. John Caldwell provided invaluable insight into agricultural production systems in Mali. He also served as my primary technical advisor for the biological component of the model. Most importantly, however, I would like to thank my committee chair, Dr. Daniel Taylor. Dan provided both guidance and encouragement while allowing me the intellectual freedom to identify and pursue my own interests, for which I am grateful. In addition to his many professional contributions, Dan has served as a model dignity and courage for my personal life. His strength and commitment to family in the face of truly adverse conditions will be, without doubt, the most enduring lesson of my tenure at Virginia Tech. And, finally, my deepest thanks go to my wife, Susan, and my two children, Madeleine Jane and Joseph Justis, for their countless personal sacrifices. Without the emotional support they provided throughout, this study would not have been completed. Their names belong on my diploma as well. iv Table of Contents Abstract ................................................................................................................................. ii Acknowledgements ............................................................................................................... iv Table of Contents .................................................................................................................. v List of Tables......................................................................................................................... ix List of Figures ....................................................................................................................... xvi Chapter 1: Introduction Section 1.1: Introduction......................................................................................................1 Section 1.2: Basic Biological Characteristics of Striga ....................................................... 2 Section 1.3: Problem Statement ........................................................................................... 3 Section 1.4: Objectives......................................................................................................... 6 Section 1.5: Organization of the Dissertation ...................................................................... 7 Chapter 2: Literature Review Section 2.1: Introduction......................................................................................................9 Section 2.2: Striga Population Models................................................................................. 9 Section 2.3: Effects of Nitrogen Fertilizers on the Biological Parameters .......................... 18 Section 2.4: Effects of Hand-Pulling on the Biological Parameters .................................... 28 Section 2.5: Effects of Chemical Controls on the Biological Parameters............................ 29 Chapter 3: Methodology Section 3.1: Introduction......................................................................................................41 Section 3.2: Modeling Striga Population Dynamics............................................................ 41 v Section 3.3: The Economic Component............................................................................... 45 Section 3.4: Estimating the Value of Striga Eradication ..................................................... 46 Section 3.5: Identifying Barriers to Adoption...................................................................... 48 Section 3.6: Concluding Remarks on the Methodology ...................................................... 53 Chapter 4: The Economic Component Section 4.1: Introduction......................................................................................................55 Section 4.2: Defining the Representative Agricultural Production Unit.............................. 55 Section 4.3: Defining the Land Constraint........................................................................... 59 Section 4.4: Crop Associations Available in the Model ...................................................... 61 Section 4.5: Defining the Labor Constraint ......................................................................... 61 Section 4.6: Crop Production Functions .............................................................................. 66 Section 4.7: Defining the Cash Constraint........................................................................... 73 Section 4.8: Defining the Nutritional Constraint ................................................................. 74 Section 4.9: Input and Output Prices and the Discount Rate ............................................... 74 Section 4.10: Estimating the UP’s “Planning Horizon”....................................................... 76 Section 4.11: Concluding Remarks on the Economic Component ...................................... 78 vi Chapter 5: The Biological Component Section 5.1: Introduction......................................................................................................82 Section 5.2: Probability of Stimulation................................................................................82 Section 5.3: Probability of Germination..............................................................................86 Section 5.4: Probability of Attachment................................................................................86 Section 5.5: Probability of Emergence.................................................................................88 Section 5.6: Probability of Reproduction.............................................................................91
Load more

Recommended publications
  • MALI - Reference Map
    MALI - Reference Map !^ Capital of State !. Capital of region ® !( Capital of cercle ! Village o International airport M a u r ii t a n ii a A ll g e r ii a p Secondary airport Asphalted road Modern ground road, permanent practicability Vehicle track, permanent practicability Vehicle track, seasonal practicability Improved track, permanent practicability Tracks Landcover Open grassland with sparse shrubs Railway Cities Closed grassland Tesalit River (! Sandy desert and dunes Deciduous shrubland with sparse trees Region boundary Stony desert Deciduous woodland Region of Kidal State Boundary ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! Bare rock ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! Mosaic Forest / Savanna ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! Region of Tombouctou ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! 0 100 200 Croplands (>50%) Swamp bushland and grassland !. Kidal Km Croplands with open woody vegetation Mosaic Forest / Croplands Map Doc Name: OCHA_RefMap_Draft_v9_111012 Irrigated croplands Submontane forest (900 -1500 m) Creation Date: 12 October 2011 Updated:
    [Show full text]
  • FINAL REPORT Quantitative Instrument to Measure Commune
    FINAL REPORT Quantitative Instrument to Measure Commune Effectiveness Prepared for United States Agency for International Development (USAID) Mali Mission, Democracy and Governance (DG) Team Prepared by Dr. Lynette Wood, Team Leader Leslie Fox, Senior Democracy and Governance Specialist ARD, Inc. 159 Bank Street, Third Floor Burlington, VT 05401 USA Telephone: (802) 658-3890 FAX: (802) 658-4247 in cooperation with Bakary Doumbia, Survey and Data Management Specialist InfoStat, Bamako, Mali under the USAID Broadening Access and Strengthening Input Market Systems (BASIS) indefinite quantity contract November 2000 Table of Contents ACRONYMS AND ABBREVIATIONS.......................................................................... i EXECUTIVE SUMMARY............................................................................................... ii 1 INDICATORS OF AN EFFECTIVE COMMUNE............................................... 1 1.1 THE DEMOCRATIC GOVERNANCE STRATEGIC OBJECTIVE..............................................1 1.2 THE EFFECTIVE COMMUNE: A DEVELOPMENT HYPOTHESIS..........................................2 1.2.1 The Development Problem: The Sound of One Hand Clapping ............................ 3 1.3 THE STRATEGIC GOAL – THE COMMUNE AS AN EFFECTIVE ARENA OF DEMOCRATIC LOCAL GOVERNANCE ............................................................................4 1.3.1 The Logic Underlying the Strategic Goal........................................................... 4 1.3.2 Illustrative Indicators: Measuring Performance at the
    [Show full text]
  • Sur Les Polluants Organiques Persistants
    REPUBLIQUE DU MALI ORGANISATION DES NATIONS UNIES Ministère de L’environnement Programme des Nations Unies pour Et de l’Assainissement L’Environnement PLAN NATIONAL DE MISE EN ŒUVRE DE LA CONVENTION DE STOCKHOLM Sur les Polluants Organiques Persistants Mai 2006 REPUBLIQUE DU MALI Un Peuple – Un But – Une Foi *****0***** MINISTERE DE L’ENVIRONNEMENT ET DE L’ASSAINISSEMENT *****0***** Direction Nationale de l’Assainissement et du Contrôle des Pollutions et des Nuisances *****0***** PLAN NATIONAL DE MISE EN ŒUVRE DE LA CONVENTION DE STOCKHOLM Sur les Polluants Organiques Persistants *****0***** Mai 2006 PREFACE 2 Mr. Lamine THERA Coordinateur et Point Focal Projet POPs Mali La Convention de Stockholm sur les Polluants Organiques Persistants (POPs) à été ratifiée par le Mali le 20 mai 2003. Elle marque une prise de conscience élevée de la Communauté Internationale des graves conséquences liées à la dégradation de l’environnement, de la santé humaine et faunique. Pour protéger et utiliser durablement l’environnement et particulièrement la santé des êtres vivants, le Gouvernement du Mali, par un large processus participatif a élaboré le présent Plan National de Mise en œuvre (PNM) qui intègre tous les aspects du concept de protection de l’environnement et de la santé contre les Polluants Organiques Persistants. La préparation de ce Plan National de mise en œuvre a fourni l’opportunité de faire l’état des lieux en matière de ressources naturelles, d'écosystèmes et de politiques appliquées dans ces domaines. La richesse de l’environnement au Mali s’observe dans les nombreuses espèces de plantes, de fleuves, d’animaux qui ont colonisé les différentes zones bioclimatiques.
    [Show full text]
  • IMRAP, Interpeace. Self-Portrait of Mali on the Obstacles to Peace. March 2015
    SELF-PORTRAIT OF MALI Malian Institute of Action Research for Peace Tel : +223 20 22 18 48 [email protected] www.imrap-mali.org SELF-PORTRAIT OF MALI on the Obstacles to Peace Regional Office for West Africa Tel : +225 22 42 33 41 [email protected] www.interpeace.org on the Obstacles to Peace United Nations In partnership with United Nations Thanks to the financial support of: ISBN 978 9966 1666 7 8 March 2015 As well as the institutional support of: March 2015 9 789966 166678 Self-Portrait of Mali on the Obstacles to Peace IMRAP 2 A Self-Portrait of Mali on the Obstacles to Peace Institute of Action Research for Peace (IMRAP) Badalabougou Est Av. de l’OUA, rue 27, porte 357 Tel : +223 20 22 18 48 Email : [email protected] Website : www.imrap-mali.org The contents of this report do not reflect the official opinion of the donors. The responsibility and the respective points of view lie exclusively with the persons consulted and the authors. Cover photo : A young adult expressing his point of view during a heterogeneous focus group in Gao town in June 2014. Back cover : From top to bottom: (i) Focus group in the Ségou region, in January 2014, (ii) Focus group of women at the Mberra refugee camp in Mauritania in September 2014, (iii) Individual interview in Sikasso region in March 2014. ISBN: 9 789 9661 6667 8 Copyright: © IMRAP and Interpeace 2015. All rights reserved. Published in March 2015 This document is a translation of the report L’Autoportrait du Mali sur les obstacles à la paix, originally written in French.
    [Show full text]
  • Académie D'enseignement De KOULIKORO
    MINISTERE DE L'EDUCATION NATIONALE REPUBLIQUE DU MALI ----------------------- Un Peuple - Un But - Une Foi ------------------- SECRETARIAT GENERAL DECISION N° 20 13- / MEN- SG PORTANT ORIENTATION DES ELEVES TITULAIRES DU D.E.F, SESSION DE JUIN 2013, AU TITRE DE L'ANNEE SCOLAIRE 2013-2014. LE MINISTRE DE L'EDUCATION NATIONALE, Vu la Constitution ; Vu le Décret N°2013-721/P-RM du 8 septembre 2013 portant nomination des membres du Gouvernement ; Vu l'Arrêté N° 09 - 2491 / MEALN-SG du 10 septembre 2009 fixant les critères d’orientation, de transfert, de réorientation et de régularisation des titulaires du Diplôme d’Etudes Fondamentales (DEF) dans les Etablissements d’Enseignement Secondaire Général, Technique et Professionnel ; Vu la Décision N°10-2742/MEALN-SG-CPS du 04 juin 2010 déterminant la composition, les attributions et modalités de travail de la commission nationale et du comité régional d'orientation des élèves titulaires du diplôme d'études fondamentales (DEF), session de juin 2010 ; Vu la décision N°2011-03512 / MEALN–SG-IES du 19 Août 2011 fixant la Liste des Etablissements Privés d'Enseignement Secondaire éligibles pour accueillir des titulaires du Diplôme d'Etudes Fondamentales (DEF) pris en charge par l’Etat ; Vu la décision N° 2011-03614 / MEALN–SG-IES du 07 Septembre 2011 fixant la Liste additive des Etablissements Privés d'Enseignement Secondaire éligibles pour accueillir des titulaires du Diplôme d'Etudes Fondamentales (DEF) pris en charge par l’Etat ; Vu la décision N° 2011-03627 / MEALN–SG-IES du 09 Septembre 2011 fixant
    [Show full text]
  • World Bank Document
    Document of The World Bank FOR OFFICIAL USE ONLY Public Disclosure Authorized Report No: 32130 IMPLEMENTATION COMPLETION REPORT (IDA-26170) ON A CREDIT Public Disclosure Authorized IN THE AMOUNT OF SDR 46.1 MILLION (US$ 65 MILLION EQUIVALENT) TO THE REPUBLIC OF MALI FOR A TRANSPORT SECTOR PROJECT Public Disclosure Authorized June 20, 2005 Transport Sector Country Department 15 Africa Region This document has a restricted distribution and may be used by recipients only in the performance of their Public Disclosure Authorized official duties. Its contents may not otherwise be disclosed without World Bank authorization. CURRENCY EQUIVALENTS (Exchange Rate Effective May 5, 1994 - December 31, 2004) Currency Unit = CFA Franc (CFAF) 1CFAF = US$ 0.0016 US$ 1.00 = CFAF 600 US$ 1.00 = CFAF 602.4 (average during project life) FISCAL YEAR January 1 to December 31 ABBREVIATIONS AND ACRONYMS ABEDA - Arab Bank for Economic Development in Africa ADM - Aéroports du Mali (Mali Airports) ASECNA - Agency for the Safety of Aerial Navigation in Africa and Madagascar BOAD - Banque Ouest Africaine de Développement (West African Development Bank) CEAO - Communauté Economique de l’Afrique de l'Ouest (West African Economic Community) CFD - Caisse Française de Développement (French Development Fund) CIDA - Canadian International Development Agency CIF - Cost, Insurance and Freight (border point price) CMDT - Compagnie Malienne de Développement des Textiles (Malian Textile Development Company) CNREX - Centre National de Recherche et d'Expérimentation pour le Bâtiment
    [Show full text]
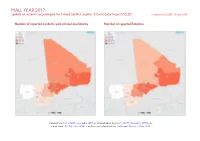
  • ACLED) Compiled by ACCORD, 18 June 2018
    MALI, YEAR 2017: Update on incidents according to the Armed Conflict Location & Event Data Project (ACLED) compiled by ACCORD, 18 June 2018 Number of reported incidents with at least one fatality Number of reported fatalities National borders: GADM, November 2015a; administrative divisions: GADM, November 2015b; in- cident data: ACLED, June 2018; coastlines and inland waters: Smith and Wessel, 1 May 2015 MALI, YEAR 2017: UPDATE ON INCIDENTS ACCORDING TO THE ARMED CONFLICT LOCATION & EVENT DATA PROJECT (ACLED) COMPILED BY ACCORD, 18 JUNE 2018 Contents Conflict incidents by category Number of Number of reported fatalities 1 Number of Number of Category incidents with at incidents fatalities Number of reported incidents with at least one fatality 1 least one fatality Battles 191 107 620 Conflict incidents by category 2 Violence against civilians 132 79 238 Development of conflict incidents from 2008 to 2017 2 Remote violence 92 29 89 Riots/protests 31 2 2 Methodology 3 Strategic developments 22 0 0 Conflict incidents per province 4 Non-violent activities 6 0 0 Localization of conflict incidents 4 Total 474 217 949 This table is based on data from ACLED (datasets used: ACLED, June 2018). Disclaimer 5 Development of conflict incidents from 2008 to 2017 This graph is based on data from ACLED (datasets used: ACLED, June 2018). 2 MALI, YEAR 2017: UPDATE ON INCIDENTS ACCORDING TO THE ARMED CONFLICT LOCATION & EVENT DATA PROJECT (ACLED) COMPILED BY ACCORD, 18 JUNE 2018 Methodology an incident occured, or the provincial capital may be used if only the province is known. Erroneous location data, especially due to identical place names, cannot The data used in this report was collected by the Armed Conflict Location & Event be fully excluded.
    [Show full text]
  • M650kv1906mlia1p-Mliadm22302-Koulikoro.Pdf (French (Français))
    RÉGION DE KOULIKORO - MALI Map No: MLIADM22302 9°0'W 8°0'W 7°0'W 6°0'W M A U R I T A N I E ! ! ! Mo!ila Mantionga Hamd!allaye Guirel Bineou Niakate Sam!anko Diakoya ! Kassakare ! Garnen El Hassane ! Mborie ! ! Tint!ane ! Bague Guessery Ballé Mou! nta ! Bou!ras ! Koronga! Diakoya !Palaly Sar!era ! Tedouma Nbordat!i ! Guen!eibé ! Diontessegue Bassaka ! Kolal ! ! ! Our-Barka Liboize Idabouk ! Siramani Peulh Allahina ! ! ! Guimbatti Moneke Baniere Koré ! Chedem 1 ! 7 ! ! Tiap! ato Chegue Dankel Moussaweli Nara ! ! ! Bofo! nde Korera Koré ! Sekelo ! Dally ! Bamb!oyaha N'Dourba N 1 Boulal Hi!rte ! Tanganagaba ! S É G O U ! Djingodji N N ' Reke!rkaye ' To!le 0 Boulambougou Dilly Dembassala 0 ° ! ! ! ° 5 ! ! 5 1 Fogoty Goumbou 1 Boug!oufie Fero!bes ! Mouraka N A R A Fiah ! ! Dabaye Ourdo-Matia G!nigna-Diawara ! ! ! Kaw! ari ! Boudjiguire Ngalabougou ! ! Bourdiadie Groumera Dabaye Dembamare ! Torog! ome ! Tarbakaro ! Magnyambougou Dogofryba K12 ! Louady! Cherif ! Sokolo N'Tjib! ougou ! Warwassi ! Diabaly Guiré Ntomb!ougou ! Boro! dio Benco Moribougou ! ! Fallou ! Bangolo K A Y E S ! Diéma Sanabougou Dioumara ! ! ! Diag! ala Kamalendou!gou ! Guerigabougou ! Naou! lena N'Tomodo Kolo!mina Dianguirdé ! ! ! ! Mourdiah ! N'Tjibougou Kolonkoroba Bekelo Ouolo! koro ! Gomitra ! ! Douabougou ! Mpete Bolib! ana Koira Bougouni N16 ! Sira! do Madina-Kagoro ! ! N'Débougou Toumboula Sirao!uma Sanmana ! ! ! Dessela Djemene ! ! ! Werekéla N8 N'Gai Ntom! ono Diadiekabougou ! ! Dalibougou !Siribila ! ! Barassafe Molodo-Centre Niono Tiemabougou ! Sirado ! Tallan ! ! Begn!inga ! ! Dando! ugou Toukoni Kounako Dossorola ! Salle Siguima ! Keke Magassi ! ! Kon!goy Ou!aro ! Dampha Ma!rela Bal!lala ! Dou!bala ! Segue D.T.
    [Show full text]
  • Crise Alimentaire : Enjeux Et
    REPUBLIQUE DU MALI Un Peuple ± Un But ± Une Foi Ministère du Développement Social, Programme des Nations de la Solidarité et des Personnes Âgées Unies pour le Développement ------------ Observatoire du Développement Humain Durable et de la Lutte Contre la Pauvreté Mali RAPPORT NATIONAL SUR LE DEVELOPPEMENT HUMAIN DURABLE, Edition 2010 Crise alimentaire : enjeux et opportunités pour le développement du secteur agricole Mars 2010 Crise alimentaire : enjeux et opportunités pour le développement du secteur agricole ÉQUIPE D¶ELABORATION DU RNDH, EDITION 2010 Supervision Générale Sékou DIAKITÉ Ministre du Développement Social, de la Solidarité et des Personnes Âgées Madame Mbaranga GASARABW E Coordonnateur Résident du Système des Nations Unies (SNU) au Mali Coordination Technique Amadou ROUAMBA Secrétaire Général MDSSPA Koulou FANÉ Conseiller Technique MDSSPA Zoumana B. FOFANA Directeur Général ODHD Luc Joëlle GRÉGOIRE Economiste Principal du PNUD Alassane B A Economiste national du PNUD Equipe ODHD/LCP Personnel technique Zoumana B. FOFANA Directeur Général Dramane L. TRAORÉ Expert Économiste Idrissa A. TRAORÉ Économiste planificateur Bouréma F. BALLO Expert Statisticien Mody SIMPARA Statisticien Soumaïla OULALÉ Sociologue Mahamadou WAGUÉ Documentaliste Madame Maïga Mariam M AÎGA Sociologue Ely DIARRA Économiste- Informaticien Abdoulaye dit Noël CISSOKO Chargé de Communication Administration et Gestion Madame Sidibé Mariam T. TRAORÉ Agent Comptable Madame Kadiatou DICKO Assistante d¶équipe Madame Niaré Hawa KARAMBÉ Secrétaire Equipe PNUD Luc Joëlle GRÉGOIRE Economiste Principal du PNUD, Unité économique Alassane BA Economiste national du PNUD, Unité économique Comité de Pilotage Président Koulou FANÉ MDSSPA Membres Sékouba DIARRA CT CSLP Séydou Moussa TRAORÉ INSTAT Madame Sidibé Fatoumata DICKO DNP Sékou M AÏGA PACR Madame Sy Kadiatou SOW PADEC Youssouf KONÉ IER Issa SACKO Université de Bamako Modibo DOLO DNPD Eloi OUÉDRAOGO Afristat Boureima Alaye TOURÉ CNSC Ibrahima KAMPO CESC Zoumana B.
    [Show full text]
  • Mli0008 Ref Region De Koulikoro A3 15092013
    MALI - Région de Koulikoro : Carte de référence (Septembre 2013) Limite d'Etat MAURITANIE Limite de Région Limite de Cercle Dogofrey Koronga Limite de Commune Gueneibe Allahina .! Chef-lieu de Région ! NARA ! Chef-lieu de Cercle Dilly Dabo Ouagadou CERCLES BANAMBA Guire DIOÏLA KANGABA Fallou KATI Niamana KOLOKANI KOULIKORO NARA Sagabala Boron Sebete SEGOU Djidjeni Toubacoro Madina Sacko Sebekoro 1 Toucoroba KOLOKANI Ben Kadi Kiban ! ! KAYES Massantola BANAMBA Guihoyo Nyamina Tioribougou Duguwolowula Daban Sirakorola Nonkon Ouolodo Tougouni N'tjiba Doumba Diedougou Nonssombougou Koula Dinandougou Kalifabougou Yelekebougou Meguetan Kambila Tienfala KOULIKORO Bossofala Dio-gare .!! Safo Binko Diago KATI Zan Guegneka ! Moribabougou Coulibaly ( Fana ) Doubabougou Kerela Nangola Sangarebougou N'gabacoro Droit Dombila Dogodouman Tenindougou Wacoro Baguineda Diouman Dolendougou BAMAKO Camp Sobra Kalaban-coro DIOÏLA Mande ! Diedougou Mountougoula Kaladougou Nioumamakana Siby N'gouraba Kilidougou N'garadougou Benkadi Sanankoroba Jekafo Bougoula Degnekoro Balan Narena Tiele Diebe N'dlondougou Cette carte a été réalisée selon le découpage Bakana Bancoumana Dialakoroba administratif du Mali à partir des données de la Karan Kemekafo N'golobougou Direction Nationale des Collectivités Niagadina Sanankoro Banco Territoriales (DNCT) Kourouba Djitoumou Benkadi KANGABA Ouelessebougou Minidian ! Faraba Massigui Nom de la carte: Maramandougou MLI0008 REF REGION DE KOULIKORO A3 15092013 Kaniogo Niantjila Tiakadougou SIKASSO Date de création: Septembre 2013
    [Show full text]
  • Emergency Support to Vulnerable Households Affected by the Early Agropastoral Lean Season in Nara District, Mali COOPERATIVE
    Emergency Support to Vulnerable Households Affected by the Early Agropastoral Lean Season in Nara District, Mali COOPERATIVE AGREEMENT 72DFFP18GR00060 Third Quarter Report January 1, 2019 – March 31, 2019 Submitted to: Office of Food for Peace, USAID Submission Date: April 24, 2019 1. Key information Implementing Agency: International Rescue Committee National Office: Badalabougou Est, Bamako, Mali Franck Vannetelle, IRC Mali Country Director Email: [email protected] Telephone: +223 71287791 Agency Headquarters: International Rescue Committee 122 East 42nd Street, New York, NY 10168, USA Telephone: + 1 (212) 551-3015 Fax: + 1 (212) 551-3185 Erika Pearl, Program Officer E-mail: [email protected] Project Title: Emergency Support to Vulnerable Households Affected by the Early Agropastoral Lean Season in Nara District, Mali Project Duration: August 1, 2018 – July 31, 2019 Program Goal: To contribute to the sustainable improvement of food security and nutritional status for vulnerable households in Nara district, Mali Budget: $1,986,968 Total beneficiaries targeted: 4,936 households (34,552 individuals) Total beneficiaries reached in the reporting period: 4,936 households (44,325 individuals) Total beneficiaries reached cumulatively: 44,325 individuals 1 I. Background The security situation remained relatively calm during the period from January to March 2019. No incidents or accidents impacted the implementation of project activities. Though there was an increase in the Malian military patrols in the commune of Niamana, one of the six communes where the FFP project is implemented no incidents impacted the implementation of the FFP project activities. During this reporting period, transhumant herders from Mauritania continued to return to the circle of Nara, albeit in fewer numbers compared to the same period in previous years.
    [Show full text]
  • Cercle De Nara, Région De Koulikoro Du 20/05/13 Au 02/06/2013
    Rapport de diagnostic multisectoriel Direction Régionale de la Protection Civile de Koulikoro Lieu d’intervention: Cercle de Nara, Région de Koulikoro Du 20/05/13 au 02/06/2013 Sommaire 1. Introduction 2. Synthèse des observations et problèmes rencontrés 3. Contexte de la zone d’intervention 4. Conclusion du diagnostic 5. Synthèse des Recommandations Nara Région Koulikoro Cercle Nara Commune Coordonnées GPS Commune Coordonnées GPS Mourdiah 7°28'16'' O 14°28'18'' N Koronga 7°36'29'' O 15°19'60'' N Fallou 7°55'46'' O 14°35'52'' N Nara 7°17'16'' O 15°10'1'' N Cercle de Boulal 8°25'37'' O 15°4'51'' N Goumbou 7°27'14'' O 14°59'27'' N – Allahina 8°44'14'' O 15°13'39'' N Gueneibe 7°5'18'' O 15°16'56'' N Ballé 8°35'4'' O 15°20'22'' N Guire 6°41'38'' O 14°38'37'' N Dilly 7°40'7'' O 14°59'46'' N Pour tout complément d’information, Contact : Fabien CASSAN, Coordinateur Qualité, Monitoring et Evaluation Tel : +223 78 06 90 39 Email : [email protected] 1 Diagnostic Rapport de diagnostic multisectoriel Direction Régionale de la Protection Civile de Koulikoro 1. Introduction 1. Présentation du diagnostic Ce diagnostic multisectoriel s’inscrit dans le cadre du projet Eau Hygiène et Assainissement (EHA) de Solidarités International dans les cercles de Kolokani et Nara « Amélioration de l’accès à des infrastructures Eau, Assainissement, Hygiène par une approche communautaire et un renforcement des capacités locales », financé par UNICEF, dont l’un des objectifs est d’améliorer la connaissance de ces zones en termes de couverture EHA, Sécurité Alimentaire et Moyens d’Existence (SAME) des populations.
    [Show full text]