A History of Theory of Structures in the Nineteenth Century
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Montreal Bridges
The METALLURGICAL HISTORYof MONTREAL BRIDGES AN ONLINE SERIES by H.J. McQueen, Concordia University PART 2 THE VICTORIA TRUSS BRIDGE (1898) — STEEL, HOT RIVETED The METALLURGICAL HISTORYof MONTREAL BRIDGES THE VICTORIA TRUSS BRIDGE (1898) — STEEL, HOT RIVETED Abstract In 1898, the Victoria Truss Bridge1 that crossed the St. ness greater than those of the original bridge. Developments in Lawrence River at Montreal was designed as a double-tracked bridge design from extensive railroad experience indicated steel truss. This new bridge replaced the original single-track that for construction to be completed in 1898, a Pratt truss box-girder and was constructed on the same piers as the origi- design would be more effective; this design would enable dou- nal bridge, which had been built half a century earlier. In the ble-tracking and the addition of roadways (Fig. 1; Szeliski, time between construction of the first and the second bridges, 1987; Victoria Jubilee Bridge, 1898). large-scale steel production had replaced wrought iron produc- Before examining the design of the Victoria Truss Bridge tion because of the cost and strength advantages of steel. This on the original piers (Fig. 2; McQueen, 1992; Szeliski, 1987; transition in Canada and its impact on bridge construction are discussed. The essential role that rivets played in bridge con- struction at this time is also described, with a focus on limited rolling capability and lack of dependable welding. Then, the addition of roadways on the outer sides of the bridge trusses are explored — these provided the first badly needed crossing for carriages and automobiles. Finally, the addition of a spur and lift spans across the Seaway are described. -
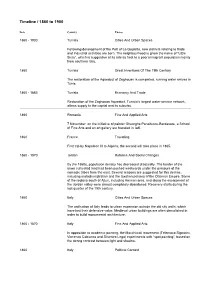
Timeline / 1860 to 1900
Timeline / 1860 to 1900 Date Country Theme 1860 - 1900 Tunisia Cities And Urban Spaces Following development of the Port of La Goulette, new districts relating to trade and industrial activities are born. The neighbourhood is given the name of “Little Sicily”, which is suggestive of its role as host to a poor immigrant population mainly from southern Italy. 1860 Tunisia Great Inventions Of The 19th Century The restoration of the Aqueduct of Zaghouan is completed, running water arrives in Tunis. 1860 - 1863 Tunisia Economy And Trade Restoration of the Zaghouan Aqueduct, Tunisia’s largest water-service network, allows supply to the capital and its suburbs. 1860 Romania Fine And Applied Arts 7 November: on the initiative of painter Gheorghe Panaitescu-Bardasare, a School of Fine Arts and an art gallery are founded in Ia#i. 1860 France Travelling First trip by Napoleon III to Algeria; the second will take place in 1865. 1860 - 1870 Jordan Reforms And Social Changes By the 1860s, population density has decreased drastically. The border of the sawn cultivated land had been pushed westwards under the pressure of the nomadic tribes from the east. Several reasons are suggested for this decline, including maladministration and the taxation policies of the Ottoman Empire. Some of the regions south of Ajlun, including Amman area, and along the escarpment of the Jordan valley were almost completely abandoned. Recovery starts during the last quarter of the 19th century. 1860 Italy Cities And Urban Spaces The unification of Italy leads to urban expansion outside the old city walls, which have lost their defensive value. -

Ynys Môn / Anglesey West (OS Sheet 115) – Gentle Ride – 27 Miles (+ 4 Mile Optional Extension to Beach.)
Ynys Môn / Anglesey West (OS sheet 115) – Gentle ride – 27 miles (+ 4 mile optional extension to beach.) Leaving through the Botanic garden and crossing the Menai Suspension bridge this ride follows lanes and cycle ways visiting some of the beaches of West Anglesey and (well worth a visit) the Marquis of Anglesey’s Column. From the Môn end of the bridge the route leaves Porthaethwy / Menai Bridge up a steady hill and continues along Sustrans Route 8 through Llanddaniel Fab towards Dwyran and the White Lodge cafe at GR 431650. Continuing along the A4080 to Newborough / Niwbwrch it is possible to extend the ride to the beautiful beach of Traeth Llanddwyn Beach - a return trip of 4 miles. (Details on route sheet.) Returning via the Malltraeth estuary and the Lon Las Cefni cycle path across the marsh it then follows the old A5 (little traffic nowadays) to *Llanfair Pwllgwyngyll (shops, cafes, toilets in ‘James Pringle Weavers’). From here the road becomes busier passing the Marquis of Anglesey’s Column – small charge – until the Suspension Bridge leads back to the campsite. *Llanfairpwllgwyngyllgogerychwyrndrobwllllantysiliogogogoch (St. Mary’s Church in a hollow by the white hazel near the rapid whirlpool and St. Tysilio’s Church by the red cave. if you must!!) Ynys Môn / Anglesey West (OS sheet 114) – Touring ride – 45 miles Leaving through the Botanic Garden and crossing the Menai Suspension bridge this ride follows the lanes and cycle ways of West and Central Anglesey viewing coast and countryside and returns via the market town of Llangefni. From the Môn end of the bridge the route leaves Porthaethwy / Menai Bridge up a steady hill, over the Four Crosses roundabout and continues along Sustrans Route 8 through Llanddaniel Fab towards Dwyran and the White Lodge cafe. -

Menai Strait Catchment Management Plan Consultation Report
f\JRA Wales 'XL MENAI STRAIT CATCHMENT MANAGEMENT PLAN CONSULTATION REPORT N.R.A - Welsh Region REGIONAL TECHNICAL (PLANNING) Reference No s RTP016 LIBRARY COPY - DO NOT REMOVE NRA National Rivers Authority Welsh Region ENVIRONMENT AGENCY WELSH REGION CATALOGUE ACCESSION CODE ENVIRONMENT AGENCY 128767 Menai Strait Catchment Management Plan Consultation Report June 1993 National Rivers Authority Welsh Region Rivers House St Mellons Business Park St Mellons Cardiff CF3 OLT Further copies can be obtained from The Catchment Planning Coordinator A r e a Catchment Planning Coordinator National Rivers Authority National Rivers Authority Welsh Region Bryn Menai Rivers House or Holyhead Road St Mellons Bussiness Park Bangor St Mellons Gwynedd Cardiff LL57 2EF CF3 OTL Telephone Enquiries : Cardiff (0222) 770088 Bangor (0248) 370970 MENAI CATCHMENT MANAGEMENT PLAN CONTENTS PAGE No. 1.0 CONCEPT 3 2.0 OVERVIEW 5 2.1 Introduction 2.2 Population 2.3 Land Use 6 2.4 Infrastructure 6 2.5 Geography 6 2.6 Water Quality 6 2.7 Ecology 6 2.8 Exploitation 6 2.9 Water Sports 6 Key Details 7 3.0 CATCHMENT USES 8 3.1 Development - housing, industry & commerce 8 3.2 Basic Amenity 11 3.3 Conservation/Marine Ecology 12 3.4 Special Conservation Areas 13 3.5 Marine Fisheries 15 3.6 Angling 17 3.7 Salmonid Fishery 18 3.8 Commercial Shellfishery 19 3.9 Flood Defence 21 3.10 Immersion Sports 23 3.11 Boating 24 3.12 Water Abstraction 26 3.13 Effluent Disposal 27 3.14 Scientific Research 29 3.15 Navigation 30 4.0 . -

Menai Strait Spectacular Llanfair PG to Menai Bridge on the Isle of Anglesey
Menai Strait Spectacular Llanfair PG to Menai Bridge on the Isle of Anglesey A walk of unfolding delights; not just the world famous Menai Suspension Bridge built by Telford in 1826 and the Britannia Bridge built by Stephenson in 1850, but also a mighty statue of Lord Nelson, tidal lagoons, a Church on a tiny island surrounded by the racing tides and beautiful views up and down the ever-changing Menai Strait that separates the Isle of Anglesey from mainland Britain. A walk you'll remember forever. " Distance 11.02 miles / 17.7 km Duration 4-5 hours Difficulty Easy Starting from Marquis of Anglesey's column Car Park Menai Strait Spectacular www.walkingnorthwales.co.uk !1 / !4 www.walkingnorthwales.co.uk Trail Map ! ! !Key ! ! ! ! Car Park Tourist Attraction Castle/Stately Lighthouse/Tower ! Harbour/" Walks/Trails Berth/" Flora Café/Restaurant Mooring ! Sculpture/" Place of" Bridge/River Accommodation Monument Worship Crossing Public! House/Bar ! ! ! Menai Strait Spectacular www.walkingnorthwales.co.uk !2 / !4 Chapters ! Chapter 1 Arrival and the Marquess of Anglesey Column The walk begins at parking lot below the Marquis of Anglesey's column. The first thing to do is follow the trail through the small woodland to the Column, which is well worth a visit, and is described in features. The view from the top gives a wonderful panorama across the Menai Strait to the rugged hills and mountains of Snowdonia. It also shows you the walk you're about to enjoy, exploring the shoreline of the Strait. Once !back down exit the parking lot onto to the main road and turn right. -

Wilhelm Ritter: Teacher of Maillart and Ammann
Wilhelm Ritter: teacher of Maillart and Ammann Autor(en): Billington, David P. Objekttyp: Article Zeitschrift: Ingénieurs et architectes suisses Band (Jahr): 113 (1987) Heft 7 PDF erstellt am: 05.10.2021 Persistenter Link: http://doi.org/10.5169/seals-76366 Nutzungsbedingungen Die ETH-Bibliothek ist Anbieterin der digitalisierten Zeitschriften. Sie besitzt keine Urheberrechte an den Inhalten der Zeitschriften. Die Rechte liegen in der Regel bei den Herausgebern. Die auf der Plattform e-periodica veröffentlichten Dokumente stehen für nicht-kommerzielle Zwecke in Lehre und Forschung sowie für die private Nutzung frei zur Verfügung. Einzelne Dateien oder Ausdrucke aus diesem Angebot können zusammen mit diesen Nutzungsbedingungen und den korrekten Herkunftsbezeichnungen weitergegeben werden. Das Veröffentlichen von Bildern in Print- und Online-Publikationen ist nur mit vorheriger Genehmigung der Rechteinhaber erlaubt. Die systematische Speicherung von Teilen des elektronischen Angebots auf anderen Servern bedarf ebenfalls des schriftlichen Einverständnisses der Rechteinhaber. Haftungsausschluss Alle Angaben erfolgen ohne Gewähr für Vollständigkeit oder Richtigkeit. Es wird keine Haftung übernommen für Schäden durch die Verwendung von Informationen aus diesem Online-Angebot oder durch das Fehlen von Informationen. Dies gilt auch für Inhalte Dritter, die über dieses Angebot zugänglich sind. Ein Dienst der ETH-Bibliothek ETH Zürich, Rämistrasse 101, 8092 Zürich, Schweiz, www.library.ethz.ch http://www.e-periodica.ch CHRISTIAN MENN Ingénieurs el architectes suisses n" 7 26 mars 1987 Tableau 1. — Amplitudes maximales des variations de températures uniformes les ponts selon différentes sources. pour Bibliographie à Taa [°C] [1] J accoud, J.-P. Gradients de tempéra¬ dans les et Ponts en bétons Ponts mixtes Ponts en acier ture ponts. -

FORM and FORCE 7-10 October 2019, Barcelona, Spain
60th Anniversary Symposium of the International Association for Shell and Spatial Structures IASS Symposium 2019 9th International Conference on Textile Composites and Inflatable Structures Structural Membranes 2019 FORM and FORCE 7-10 October 2019, Barcelona, Spain Carlos Lázaro, Kai-Uwe Bletzinger and Eugenio Oñate (Eds.) IASS Symposium 2019 60th Anniversary Symposium of the International Association for Shell and Spatial Structures Structural Membranes 2019 9th International Conference on Textile Composites and Inflatable Structures FORM and FORCE Barcelona, Spain October 7 - 10, 2019 A publication of: International Centre for Numerical Methods in Engineering (CIMNE) Barcelona, Spain ISBN: 978-84-121101-0-4 Printed by: Artes Gráficas Torres S.L., Huelva 9, 08940 Cornellà de Llobregat, Spain SUMMARY SUMMARY INVITED SESSIONS IS - Actual Structural Behavior of Thin Shells (IASS WG 5) ...................................... 45 IS - Adaptive Lightweight Structures .................................................................. 68 IS - Additive Manufacturing of Architectural Components........................................ 87 IS - Analysis and Design of Adaptive Structures ...................................................121 IS - Bio-inspiration for Structural Forms + Fractal and Form ...................................129 IS - Celebrating the Work of Mike Barnes ............................................................145 IS - Constructive Geometry for Structural Design (IASS WG 15) ...............................175 IS - Contemporary -

D-BAUG Jahresbericht 2016 Annual Report 2016
D-BAUG Jahresbericht 2016 Annual Report 2016 New perspectives DBAUG Departement Bau, Umwelt und Geomatik Department of Civil, Environmental and Geomatic Engineering 10 12 22 Prof. Willi H. Hager Emeritierung/Pensionierung ETH-Ehrendoktor für Max Ernst Meyer Bauingenieur und ETH Professor Carl Culmann 24 34 40 Das «Goldene Dreirad» für Prof. Lorenz Hurni Master Leistungsstipendien: Viviane Furrer D-BAUG Studenten in Havanna 52 55 73 Interview mit Prof. Thomas Vogel Gotthard Basis Tunnel: Zwei ETH Alumni berichten Neuer 3D-Atlas für Kartenliebhaber INHALT Vorwort i Gotthard Basis Tunnel: Zwei ETH Alumni berichten über ihre Erfahrungen 55 FAKULTÄT UND CAMPUS Studierendenzahlen 60 Neu am D-BAUG 2 FORSCHUNG UND LEHRE Emeritierungen/Pensionierungen 10 Eröffnung des Gotthard Basistunnels 64 ETH-Ehrendoktor für Brückenbauer Max Ernst Meyer 12 Gottardino Event 68 Stephan Pfister, IfU 14 Wo im Gotthard-Basistunnel ETH und D-BAUG drinsteckt 70 Umweltbewertung der globalen Landwirtschaftlichen Produktion 16 Neuer 3D-Atlas für Kartenliebhaber 74 Othmar Frei, IfU 18 Mit Holz und Robotern zur eigenen Firma 78 Entwicklung eines fahrzeuggestützten Spin-off Swiss Wood Solutions AG 80 abbildenden Radarinterferometers 20 Frühwarnsystem für Lawinen und Carl Culmann (1821–1881) 22 Europäisches Patent 82 Motivieren mit Instinkt 24 FAKTEN UND ZAHLEN Goldene Eule des VSETH 26 Institute und Professuren 86 “International Map Year”: Aktivitäten in der Schweiz 28 Fachgebiete innerhalb der strategischen Schwerpunkte 88 DONATOREN UND TALENTE Organisation D-BAUG 92 Donatoren D-BAUG 2016 32 Advisory Board und Fakultät 93 Master Leistungsstipendien Kennzahlen 94 (ESOP und MSP) 34 Ehrungen 96 Kontakte 99 STUDIERENDE UND ALUMNI Stab 100 AIV BauingenieurinnenFORUM 2016 36 Havanna Sommer Schule 38 KLIMASCHUTZPROJEKT 102 Eindrücke von Havanna aus Sicht der D-BAUG Studierenden 40 IMPRESSUM 103 Masterarbeit MIT, Cambridge, MA/USA 44 Masterreise nach China 48 LAGEPLAN 104 Interview mit Prof. -

Ffordd Y Gogledd the North Wales Way a Short Trip Through the Centuries Thewalesway.Com
Ffordd y Gogledd The North Wales Way A short trip through the centuries thewalesway.com northeastwales.wales visitconwy.org.uk visitsnowdonia.info visitanglesey.co.uk Where is Wales? Getting here. Wales is accessible to all major UK cities including London, Birmingham, Manchester and Liverpool. Wales is served by its own international airport, Cardiff International Airport (CWL) which has more than 50 direct routes, including major European cities and over 1,000 world wide connecting destinations. Wales is also easily served by Bristol (BRS), Birmingham (BHX), Manchester (MAN) and Liverpool (LPL) airports. 2 hours by train from London 3 hours by motorway from central London, 1 hour by road from Liverpool, Manchester, Bristol and Birmingham. Cardiff Airport has direct flights across Europe and global links via Doha, Schipol and Dublin Airports. cardiff-airport.com Direct ferry links from Irish ports. Whilst every effort has been made to ensure accuracy in this publication, the publishers can accept no liability whatsoever for any errors, inaccuracies, or omissions, or for any matter in any way connected with or arising out of the publication of the information. Please check all prices and facilities before making your booking. When you’ve finished with the guide please forward to a friend or place in a suitable recycling container. 2 Go The Wales Way The Wales Way is one Epic journey, three distinct routes – The North Wales Way, The Coastal Way and The Cambrian Way – that lead you across castle country, along the coast and through our mountainous heartland. The North Wales Way runs for 75 miles/120km past mighty castles into the island of Anglesey. -

4H Bus Time Schedule & Line Route
4H bus time schedule & line map 4H Bangor - Holyhead View In Website Mode The 4H bus line (Bangor - Holyhead) has 2 routes. For regular weekdays, their operation hours are: (1) Bangor: 7:00 AM - 8:12 PM (2) Llangefni: 5:15 AM - 8:00 PM Use the Moovit App to ƒnd the closest 4H bus station near you and ƒnd out when is the next 4H bus arriving. Direction: Bangor 4H bus Time Schedule 42 stops Bangor Route Timetable: VIEW LINE SCHEDULE Sunday 11:08 AM - 6:58 PM Monday 7:00 AM - 8:12 PM Ysgol Y Bont, Llangefni Tuesday 7:00 AM - 8:12 PM Industrial Estate, Llangefni Wednesday 7:00 AM - 8:12 PM Nant Yr Odyn, Rhostrehwfa Thursday 7:00 AM - 8:12 PM Lon Tyddyn Mawr, Pentre-Berw Friday 7:00 AM - 8:12 PM Old Windmill, Pentre-Berw Saturday 7:00 AM - 8:12 PM Lon Felin Ferw, Llanƒhangel Ysgeiƒog Community Industrial Estate, Gaerwen War Memorial, Gaerwen 4H bus Info Direction: Bangor Police Station, Gaerwen Stops: 42 Trip Duration: 44 min Tafarn Newborough, Gaerwen Line Summary: Ysgol Y Bont, Llangefni, Industrial Estate, Llangefni, Nant Yr Odyn, Rhostrehwfa, Lon Tyddyn Mawr, Pentre-Berw, Old Windmill, Pentre- Railway Farm, Gaerwen Berw, Industrial Estate, Gaerwen, War Memorial, Gaerwen, Police Station, Gaerwen, Tafarn Tan-Y-Capel, Llanddaniel Fab Newborough, Gaerwen, Railway Farm, Gaerwen, Maes y Coed, Llanddaniel Fab Community Tan-Y-Capel, Llanddaniel Fab, Post O∆ce, Llanddaniel Fab, Star Crossroads, Post O∆ce, Llanddaniel Fab Llanfairpwllgwyngyll, Hafod, Llanfairpwllgwyngyll, Bryn Salem, Llanfairpwllgwyngyll, Station, Star Crossroads, Llanfairpwllgwyngyll -

COOPER's TUBULAR ARCH BRIDGE Hill Street Bridge New York Cast and Wrought Iron Bridges Spanning Old Erie Canal at Cedar Bay Picn
COOPER'S TUBULAR ARCH BRIDGE HAER No. NY-291 Hill Street Bridge New York Cast and Wrought Iron Bridges Spanning Old Erie Canal at Cedar Bay Picnic Area (Relocated from Canajoharie, Montgomery County» NY) Old Erie Canal State Park MY De Witt Onondaga County New York PHOTOGRAPHS REDUCED COPIES OF MEASURED DRAWINGS WRITTEN HISTORICAL AND DESCRIPTIVE DATA r HISTORIC AMERICAN ENGINEERING RECORD National Park Service Department of the Interior P.O. Box 37127 Washington, D.C. 20013-7127 HISTORIC AMERICAN ENGINEERING RECORD COOPER*S TUBULAR ARCH BRIDGE U (Hill Street Bridge) HAER NO. NY-291 Locat ion: Spans a restored portion of the old Erie Canal at the Cedar Bay Picnic Area, Old Brie Canal State Park, De Witt, Onondaga County, New York. Relocated from Canajoharie, Montgomery County, New York. UTM; y..4153.76/4765992 0&G-& Quadrangle: Syracuse East, 7.5 minute Date of Construction: 18P6-" " Designer/Builder: William B. Cooper* Division Engineer, Office of New- York State Engineer and Surveyor, designer; Melvin A. Nash, Fort Edward, New York, builder. Present Owner: New York State Office of Parks, Recreation and Historic Preservation, Central Region, Jamesville, New York. Present Use: Pedestrian bridge Significance: Cooper's Tubular Arch Bridge was built in 1886 for the Town of Canajoharie, New York by Melvin A. Nash, a Fort Edward, New York bridge builder. It is the only extant example of superstructures fabricated on the 1873 patent of civil engineer William B. Cooper, then employed on the New York State Canals. In 1975, the bridge was acquired by the Central New York State Park and Recreation Commission and moved to the Old Erie Canal State Park in De Witt, where it now carries pedestrians and service vehicles across a restored COOPER'S TUBULAR ARCH BRIDGE HAER NO. -

Water, Networks and Crossings Contents Contents
WATER , NETWORKS AND CROSSINGS CONTENTS 3 Water, networks and crossings Contents Contents .............................................................................................................................................. 164 3.1 WATER BALANCE ............................................................................................................................ 166 3.1.1 Earth ....................................................................................................................................... 166 3.1.2 Evaporation and precipitation ................................................................................................. 167 3.1.3 Runoff ..................................................................................................................................... 169 3.1.4 Static balance ......................................................................................................................... 174 3.1.5 Movement ignoring resistance................................................................................................ 175 3.1.6 Resistance .............................................................................................................................. 178 3.1.7 Erosion and sedimentation ..................................................................................................... 184 3.1.8 Hydraulic geometry of stream channels ................................................................................. 186 3.1.9 River morphology...................................................................................................................