DOCSLIB.ORG

Frederick Chopin's Prelude, Op. 28 No. 4 in E Minor

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Frederick Chopin's Prelude, Op. 28 No. 4 in E Minor FREDERICK CHOPIN’S PRELUDE, OP. 28 NO. 4 IN E MINOR: HARMONIC EXPECTATION AND VIOLATION THESIS Presented to the Graduate Council of Texas State University-San Marcos in Partial Fulfillment of the Requirements for the Degree Master of MUSIC by Clifford D. Burden, B.A. San Marcos, TX August 2013 FREDERICK CHOPIN’S PRELUDE, OP. 28 NO. 4 IN E MINOR: HARMONIC EXPECTATION AND VIOLATION Committee Members Approved: Cynthia I. Gonzales, Chair Kevin E. Mooney Sean F. Johnston Approved: J. Michael Willoughby Dean of the Graduate College COPYRIGHT by Clifford Dustin Burden 2013 FAIR USE AND AUTHOR’S PERMISSION STATEMENT Fair Use This work is protected by the Copyright Laws of the United States (Public Law 94-553, section 107). Consistent with fair use as defined in the Copyright Laws, brief quotations from this material are allowed with proper acknowledgment. Use of this material for financial gain without the author’s express written permission is not allowed. Duplication Permission As the copyright holder of this work I, Clifford Dustin Burden, authorize duplication of this work, in whole or in part, for educational or scholarly purposes only. ACKNOWLEDGEMENTS I would like to express my strongest appreciation to all who helped me throughout this process. Specifically, I extend gratitude to my thesis advisor, Dr. Cynthia Gonzales. I would not have been able to complete this thesis without her guidance, support, patience, and knowledge. I also thank my committee members, Dr. Kevin Mooney and Dr. Sean Johnston, for their suggestions, encouragement, and patience. This manuscript was submitted on May 8, 2013. v TABLE OF CONTENTS Page ACKNOWLEDGEMENTS .................................................................................................v TABLE OF CONTENTS ................................................................................................... vi LIST OF FIGURES .......................................................................................................... vii LIST OF FIGURES CONTINUED ................................................................................. viii CHAPTER I. INTRODUCTION ................................................................................................1 II. EXPECTATIONS AND VIOLATIONS ............................................................8 2.1 Violation Types ......................................................................................8 2.2 Application in Chopin’s Prelude ..........................................................13 2.3 Summary ..............................................................................................25 2.4 Other Interpretations ............................................................................44 III. CONCLUSION ................................................................................................55 BIBLIOGRAPHY ..............................................................................................................57 vi LIST OF FIGURES Figure Page 1. Implication of A1 and A2 ....................................................................................9 2. a , I Î - vi - ii Î× - V ı Progression ; b , I - iii - IV - V Progression . ............................10 3. Shared Violation ................................................................................................10 4. Potential Violation .............................................................................................12 5. Unrelated Violation ............................................................................................13 6. Chopin, Prelude in E minor, op. 28 no. 4, m. 1 .................................................14 7. a, SV example; b, PV example; c, UV example .................................................15 8. Chopin, Prelude in E minor, op. 28 no. 4, mm. 1-2 ...........................................15 9. a, Violation in m. 3; b, Implication in m. 3 .......................................................16 10. a, Implication in m. 3; b, Violation in m. 3 .....................................................18 11. a, Implication in m. 4; b, Violation in m. 4 .....................................................19 12. a, Implication in m. 4; b, Violation in m. 4 .....................................................21 13. PV - UV Pattern ................................................................................................22 14. a, PV - UV in m. 2; b, PV - UV in m. 4 ............................................................22 15. a, Implication in m. 5; b, Violation in m. 5 .....................................................23 16. Overview of mm. 1-5 .......................................................................................26 17. a, Implication in m. 6; b, Violation in m. 6 .....................................................28 vii FIGURES CONTINUED 18. Duality in mm. 5-6 ...........................................................................................29 19. a, Implication in m. 7; b, Violation in m. 7 .....................................................30 20. a, Implication in m. 8; b, Violation in m. 8 .....................................................31 21. Overview of mm. 1-7 .......................................................................................33 22. a, Implication in m. 9; b, Violation in m. 9 .....................................................34 23. a, Overview of mm. 1-9; b, Reduction of mm. 1-9 .........................................37 24. a, Summary of mm. 1-9 (2); b, Summary of mm. 1-9 (3) ...............................38 25. a, ii - vii„ Sequence; b, Jazz Sequence .............................................................39 26. Multiple Violation Levels ................................................................................41 27. a, Implication in m. 10; b, Violation in m. 10 .................................................43 28. Schachter’s Analysis ........................................................................................45 29. Schenker’s Analysis .........................................................................................47 30. London’s and Rodman’s Analysis ...................................................................48 31. Parks’s Analysis ...............................................................................................51 32. Tymoczko’s Analysis.......................................................................................52 33. Tymoczko’s Four Sequences ...........................................................................54 viii CHAPTER I INTRODUCTION In my thesis I will examine vertical components of Chopin’s Prelude in E minor, op. 28 no. 4, mm. 1-12. My approach explores the musical phenomenon referred to in music theory literature as ambiguity. Ambiguity in music exists “when what we expect does not occur, when our efforts to find specific musical norms are frustrated.”1 Given this description of ambiguity, musical analysis compares a composition to a musical syntax, which in this case is the syntax of tonal music. Syntax generates implications, while knowledge of that syntax—whether intellectual or experiential—generates expectations. When implications and expectations do not match, the result is ambiguity. In order to identify implications, I will reduce passages from the Prelude to show the harmonic configuration. By comparing harmonic reductions to the syntax of tonal music, I will determine (and notate in my analysis) where an implication occurs and if it is violated. This reductive approach is similar to that of Heinrich Schenker’s, but instead of 1Deborah Stein, Engaging Music (New York: Oxford University Press, 2005), 77. 1 2 representing underlying structures in tonal music, my analysis will represent violations of implications and their role in tonal ambiguity. An analysis of music requires one to choose the appropriate analytical technique for a given work. According to some music scholars, the application of methods used for tonal analysis to atonal or ambiguous music is impractical. For example, Leonard Meyer claimed that “it is pointless to analyze a work by Boulez in terms of techniques developed by Heinrich Schenker for the analysis of tonal music.”2 Eugene Narmour finds fault in roman-numeral analysis all together, claiming that there is a “naïve associationism inherent in the roman-numeral analysis of harmonic function…”3 Also, in Charles J. Smith’s analysis of Beethoven’s Waldstein Sonata in C major, op. 53, he states that the labels of a roman-numeral analysis “address[es] identity rather than behavior or function, not whence it comes or whither it goes.”4 The dissolution of tonality during the 19th and 20th century brought about new analytical methods such as set theory, transformational theory, 12-tone analysis, chromatic theory, and motivic analysis.5 As a result, the exclusive use of roman-numeral 2Leonard Meyer, Explaining Music: Essays and Explorations (Berkeley, CA: University of California Press, 1973), 24. 3Eugene Narmour, Beyond Schenkerism: The Need for Alternatives in Musical Analysis (Chicago, IL: University of Chicago Press, 1977), 1. 4Charles J. Smith, “The Functional Extravagance of Chromatic Chords,” Music Theory Spectrum vol. 8 (Spring 1986): 99. 5Allen Forte, The Structure of Atonal Music (New Haven and London: Yale University Press, 1973); Rudolph Reti, Tonality, Atonality, Pantonality: A Study of Some Trends in Twentieth-Century Music (Westport, CT: Greenwood Press, 1978); David Lewin,
Load more

Recommended publications
  • An Adaptive Tuning System for MIDI Pianos
    David Løberg Code Groven.Max: School of Music Western Michigan University Kalamazoo, MI 49008 USA An Adaptive Tuning [email protected] System for MIDI Pianos Groven.Max is a real-time program for mapping a renstemningsautomat, an electronic interface be- performance on a standard keyboard instrument to tween the manual and the pipes with a kind of arti- a nonstandard dynamic tuning system. It was origi- ficial intelligence that automatically adjusts the nally conceived for use with acoustic MIDI pianos, tuning dynamically during performance. This fea- but it is applicable to any tunable instrument that ture overcomes the historic limitation of the stan- accepts MIDI input. Written as a patch in the MIDI dard piano keyboard by allowing free modulation programming environment Max (available from while still preserving just-tuned intervals in www.cycling74.com), the adaptive tuning logic is all keys. modeled after a system developed by Norwegian Keyboard tunings are compromises arising from composer Eivind Groven as part of a series of just the intersection of multiple—sometimes oppos- intonation keyboard instruments begun in the ing—influences: acoustic ideals, harmonic flexibil- 1930s (Groven 1968). The patch was first used as ity, and physical constraints (to name but three). part of the Groven Piano, a digital network of Ya- Using a standard twelve-key piano keyboard, the maha Disklavier pianos, which premiered in Oslo, historical problem has been that any fixed tuning Norway, as part of the Groven Centennial in 2001 in just intonation (i.e., with acoustically pure tri- (see Figure 1). The present version of Groven.Max ads) will be limited to essentially one key.
    [Show full text]
  • MTO 20.2: Wild, Vicentino's 31-Tone Compositional Theory
    Volume 20, Number 2, June 2014 Copyright © 2014 Society for Music Theory Genus, Species and Mode in Vicentino’s 31-tone Compositional Theory Jonathan Wild NOTE: The examples for the (text-only) PDF version of this item are available online at: http://www.mtosmt.org/issues/mto.14.20.2/mto.14.20.2.wild.php KEYWORDS: Vicentino, enharmonicism, chromaticism, sixteenth century, tuning, genus, species, mode ABSTRACT: This article explores the pitch structures developed by Nicola Vicentino in his 1555 treatise L’Antica musica ridotta alla moderna prattica . I examine the rationale for his background gamut of 31 pitch classes, and document the relationships among his accounts of the genera, species, and modes, and between his and earlier accounts. Specially recorded and retuned audio examples illustrate some of the surviving enharmonic and chromatic musical passages. Received February 2014 Table of Contents Introduction [1] Tuning [4] The Archicembalo [8] Genus [10] Enharmonic division of the whole tone [13] Species [15] Mode [28] Composing in the genera [32] Conclusion [35] Introduction [1] In his treatise of 1555, L’Antica musica ridotta alla moderna prattica (henceforth L’Antica musica ), the theorist and composer Nicola Vicentino describes a tuning system comprising thirty-one tones to the octave, and presents several excerpts from compositions intended to be sung in that tuning. (1) The rich compositional theory he develops in the treatise, in concert with the few surviving musical passages, offers a tantalizing glimpse of an alternative pathway for musical development, one whose radically augmented pitch materials make possible a vast range of novel melodic gestures and harmonic successions.
    [Show full text]
  • Intervals and Transposition
    CHAPTER 3 Intervals and Transposition Interval Augmented and Simple Intervals TOPICS Octave Diminished Intervals Tuning Systems Unison Enharmonic Intervals Melodic Intervals Perfect, Major, and Minor Tritone Harmonic Intervals Intervals Inversion of Intervals Transposition Consonance and Dissonance Compound Intervals IMPORTANT Tone combinations are classifi ed in music with names that identify the pitch relationships. CONCEPTS Learning to recognize these combinations by both eye and ear is a skill fundamental to basic musicianship. Although many different tone combinations occur in music, the most basic pairing of pitches is the interval. An interval is the relationship in pitch between two tones. Intervals are named by the Intervals number of diatonic notes (notes with different letter names) that can be contained within them. For example, the whole step G to A contains only two diatonic notes (G and A) and is called a second. Figure 3.1 & ww w w Second 1 – 2 The following fi gure shows all the numbers within an octave used to identify intervals: Figure 3.2 w w & w w w w 1ww w2w w3 w4 w5 w6 w7 w8 Notice that the interval numbers shown in Figure 3.2 correspond to the scale degree numbers for the major scale. 55 3711_ben01877_Ch03pp55-72.indd 55 4/10/08 3:57:29 PM The term octave refers to the number 8, its interval number. Figure 3.3 w œ œ w & œ œ œ œ Octavew =2345678=œ1 œ w8 The interval numbered “1” (two notes of the same pitch) is called a unison. Figure 3.4 & 1 =w Unisonw The intervals that include the tonic (keynote) and the fourth and fi fth scale degrees of a Perfect, Major, and major scale are called perfect.
    [Show full text]
  • The Devil's Interval by Jerry Tachoir
    Sound Enhanced Hear the music example in the Members Only section of the PAS Web site at www.pas.org The Devil’s Interval BY JERRY TACHOIR he natural progression from consonance to dissonance and ii7 chords. In other words, Dm7 to G7 can now be A-flat m7 to resolution helps make music interesting and satisfying. G7, and both can resolve to either a C or a G-flat. Using the TMusic would be extremely bland without the use of disso- other dominant chord, D-flat (with the basic ii7 to V7 of A-flat nance. Imagine a world of parallel thirds and sixths and no dis- m7 to D-flat 7), we can substitute the other relative ii7 chord, sonance/resolution. creating the progression Dm7 to D-flat 7 which, again, can re- The prime interval requiring resolution is the tritone—an solve to either a C or a G-flat. augmented 4th or diminished 5th. Known in the early church Here are all the possibilities (Note: enharmonic spellings as the “Devil’s interval,” tritones were actually prohibited in of- were used to simplify the spelling of some chords—e.g., B in- ficial church music. Imagine Bach’s struggle to take music stead of C-flat): through its normal progression of tonic, subdominant, domi- nant, and back to tonic without the use of this interval. Dm7 G7 C Dm7 G7 Gb The tritone is the characteristic interval of all dominant bw chords, created by the “guide tones,” or the 3rd and 7th. The 4 ˙ ˙ w ˙ ˙ tritone interval can be resolved in two types of contrary motion: &4˙ ˙ w ˙ ˙ bbw one in which both notes move in by half steps, and one in which ˙ ˙ w ˙ ˙ b w both notes move out by half steps.
    [Show full text]
  • Cubase Pro Plug-In Reference 10.5.20
    Plug-in Reference Cristina Bachmann, Heiko Bischoff, Lillie Harris, Christina Kaboth, Insa Mingers, Matthias Obrecht, Sabine Pfeifer, Benjamin Schütte, Marita Sladek This PDF provides improved access for vision-impaired users. Please note that due to the complexity and number of images in this document, it is not possible to include text descriptions of images. The information in this document is subject to change without notice and does not represent a commitment on the part of Steinberg Media Technologies GmbH. The software described by this document is subject to a License Agreement and may not be copied to other media except as specifically allowed in the License Agreement. No part of this publication may be copied, reproduced, or otherwise transmitted or recorded, for any purpose, without prior written permission by Steinberg Media Technologies GmbH. Registered licensees of the product described herein may print one copy of this document for their personal use. All product and company names are ™ or ® trademarks of their respective owners. For more information, please visit www.steinberg.net/trademarks. © Steinberg Media Technologies GmbH, 2020. All rights reserved. Cubase Pro_10.5.20_en-US_2020-05-26 Table of Contents 4 Included Effect Plug-ins 4 Ambisonics Plug-ins 5 Delay Plug-ins 22 Distortion Plug-ins 46 Dynamics Plug-ins 70 EQ Plug-ins 79 Filter Plug-ins 85 Mastering Plug-ins 85 Modulation Plug-ins 100 Network Plug-ins 101 Other Plug-ins 103 Pitch Shift Plug-ins 106 Reverb Plug-ins 121 Spatial + Panner Plug-ins 123 Surround
    [Show full text]
  • Secondary Dominants (Applied Dominants)
    Dr. Barbara Murphy University of Tennessee School of Music SECONDARY DOMINANTS (APPLIED DOMINANTS) DEFINITION: A secondary dominant is an altered chord having a dominant or leading tone relationship to a chord in the key other than the tonic. An altered chord is a chord containing at least one tone that is foreign to the key. Using secondary dominants results in the tonicization of the chord of resolution. Tonicization is the process of emphasizing a chord by making it seem like the tonic for a relatively short period of time. Usually this is accomplished by embellishing the chord with a chord that has a dominant or leading tone relationship to it (a secondary dominant). ANALYSIS: Secondary dominants are analyzed as 'x/y' where: x is one of : V, V7, viio, viio/ 7, viio7 y is a major or minor triad in the key. y can be one of: Major key: ii, iii, IV, V, vi minor key: iv, V, VI y can not be a diminished or augmented triad since diminished and augmented triads do not act as tonic triads. RESOLUTION: 1. Normal resolution: x/y resolves normally to y. 2. Irregular resolution: x/y may resolve to a chord that is a substitution (primary or secondary) for y. 3. Deceptive resolution: x/y may resolve to the chord whose root is a third below the root of the y chord. PART-WRITING: The part-writing of a secondary dominant is essentially the same as for the diatonic dominant or leading tone chords: For V and V7: 1. root resolves down a fifth to the root of the next chord (normal resolution).
    [Show full text]
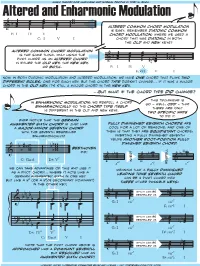
  • Altered and Enharmonic Modulation
    Altered andmusic Enharmonictheory for musicians and normal people Modulation by toby w. rush œ œ w b œ œ œ nœ w Altered common chord modulation & œ œ is easy: remember diatonic common F: I IV V chord modulation, where we used a C: I V I chord that was diatonic in both the old and new keys? altered common chord modulation is the same thing, only using the œ œ pivot chord as an altered chord & b œ œ œ #nw in either the old key, the new key, œ # #œ w or both. F: I IV V n œ E: bVI V I Now, in both diatonic modulation and altered modulation, we have one chord that plays two different roles, one for each key. But the chord type doesn’t change... if it was a major chord in the old key, it’s still a major chord in the new key. ...but...but whatwhat ifif thethe chordchord typetype did change? this technique is in enharmonic modulation, we respell a chord so — well, odd — that so the enharmonically chord type itself there are only is different in the old and new keys. two specific ways to do it. ever notice that the german augmented sixth chord is just like fully diminished seventh chords are a major-minor seventh chord cool for a lot of reasons, and one of with the seventh respelled them is that they are equidistant chords: enharmonically? inverting a fully diminshed seventh yields another root-position fully dimished seventh chord. # w bw beethoven b ww b w did! & b w bw bw bww b ∫w 7 b w C: Ger.6 D : V b w b w w b & w7 invert & 6 & 7 a° a°5 respell c° we can take advantage of this and use it meaning that a fully diminished as a pivot chord..
    [Show full text]
  • The Consecutive-Semitone Constraint on Scalar Structure: a Link Between Impressionism and Jazz1
    The Consecutive-Semitone Constraint on Scalar Structure: A Link Between Impressionism and Jazz1 Dmitri Tymoczko The diatonic scale, considered as a subset of the twelve chromatic pitch classes, possesses some remarkable mathematical properties. It is, for example, a "deep scale," containing each of the six diatonic intervals a unique number of times; it represents a "maximally even" division of the octave into seven nearly-equal parts; it is capable of participating in a "maximally smooth" cycle of transpositions that differ only by the shift of a single pitch by a single semitone; and it has "Myhill's property," in the sense that every distinct two-note diatonic interval (e.g., a third) comes in exactly two distinct chromatic varieties (e.g., major and minor). Many theorists have used these properties to describe and even explain the role of the diatonic scale in traditional tonal music.2 Tonal music, however, is not exclusively diatonic, and the two nondiatonic minor scales possess none of the properties mentioned above. Thus, to the extent that we emphasize the mathematical uniqueness of the diatonic scale, we must downplay the musical significance of the other scales, for example by treating the melodic and harmonic minor scales merely as modifications of the natural minor. The difficulty is compounded when we consider the music of the late-nineteenth and twentieth centuries, in which composers expanded their musical vocabularies to include new scales (for instance, the whole-tone and the octatonic) which again shared few of the diatonic scale's interesting characteristics. This suggests that many of the features *I would like to thank David Lewin, John Thow, and Robert Wason for their assistance in preparing this article.
    [Show full text]
  • Chapter 28.5, the Diminished Seventh Chord in Modulation
    598 THE COMPLETE MUSICIAN F. Write a progression in D minor in which the closing D tonic sounds more like a dominant than a tonic. (Hint: A Picardy third alone does not imply a reciprocal process.) G. Write a progression inC major that opens with a plagal progression, tonicizes E~ major, and closes in E~ major with a different plagal progression. The Diminished Seventh Chord and Enharmonic Modulation Beginning in the eighteenth century, composers used the diminished seventh chord both as a powerful goal-oriented applied chord and as a dramatic signpost. For example, a strategically placed diminished seventh chord could underscore a particularly emotional image from the text of a song. A vivid and painful example is heard in the last moment of Schubert's "Erlking." Immediately before we learn of the fate of the sick child ("and in [the father's] arms, the child ..."), the previous 145 measures of frantic, wildly galloping music come to a halt. The fermata that marks this moment, and which seems to last forever, is accompanied by a single sustained diminished seventh, underscoring this crucial moment (Example 28.8). We learn immediately thereafter that in spite of his valiant attempts to rush his sick son home by horseback, the father was too late: The child was dead. EXAMPLE 28.8 Schubert, "Erlkonig," D. 328 Even before the time of Bach, composers also used the diminished seventh chord to create tonal ambiguity. Ambiguity is possible because the chord in any of its inversions partitions the octave into four minor thirds (using enharmonicism). For example, given the diminished seventh chord in Example 28.9A, its three inversions produce no new intervals.
    [Show full text]
  • Enharmonic Paradoxes in Classical, Neoclassical, and Popular Music By
    Enharmonic Paradoxes in Classical, Neoclassical, and Popular Music by Haley Britt Beverburg Reale A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy (Music: Theory) in The University of Michigan 2011 Doctoral Committee: Associate Professor Ramon Satyendra, Chair Professor Walter T. Everett Professor Kevin E. Korsyn Professor Herbert Graves Winful Associate Professor Wayne C. Petty © Haley Britt Beverburg Reale 2011 Dedication36B To my husband ii Acknowledgements37B I could not have completed this dissertation without the support of numerous people. I would especially like to thank my adviser, Ramon Satyendra, for his encouragement and boundless optimism through the whole process. He never failed to receive my ideas with enthusiasm and give me the confidence to pursue them, and his wide-ranging knowledge and helpful suggestions sparked many bursts of creativity over the past several years. I would also like to thank the other members of my dissertation committee— Kevin Korsyn, Wayne Petty, Walter Everett, and Herbert Winful—for their advice and support. Their expertise in diverse subjects was invaluable to me, and they were always willing and able to answer my many questions. I also had the privilege of working with and being inspired by many other faculty members at the University of Michigan. Special thanks to Karen Fournier for being a sounding board for many of my research ideas and for being a great listener. Additionally, I would like to acknowledge the Rackham School of Graduate Studies, especially Dean Steven M. Whiting, for financial support throughout my time at the University of Michigan. The teaching assistantships, fellowships, and travel grants for presenting at conferences gave me the means to pursue my research.
    [Show full text]
  • Pitch Notation
    Pitch Notation Collection Editor: Mark A. Lackey Pitch Notation Collection Editor: Mark A. Lackey Authors: Terry B. Ewell Catherine Schmidt-Jones Online: < http://cnx.org/content/col11353/1.3/ > CONNEXIONS Rice University, Houston, Texas This selection and arrangement of content as a collection is copyrighted by Mark A. Lackey. It is licensed under the Creative Commons Attribution 3.0 license (http://creativecommons.org/licenses/by/3.0/). Collection structure revised: August 20, 2011 PDF generated: February 15, 2013 For copyright and attribution information for the modules contained in this collection, see p. 58. Table of Contents 1 The Sta ...........................................................................................1 2 The Notes on the Sta ...........................................................................5 3 Pitch: Sharp, Flat, and Natural Notes .........................................................11 4 Half Steps and Whole Steps ....................................................................15 5 Intervals ...........................................................................................21 6 Octaves and the Major-Minor Tonal System ..................................................37 7 Harmonic Series ..................................................................................45 Index ................................................................................................56 Attributions .........................................................................................58 iv Available
    [Show full text]
  • The Short Piano Works of Edward Macdowell
    City University of New York (CUNY) CUNY Academic Works Dissertations, Theses, and Capstone Projects CUNY Graduate Center 1982 The Short Piano Works of Edward MacDowell Francis Paul Brancaleone The Graduate Center, City University of New York How does access to this work benefit ou?y Let us know! More information about this work at: https://academicworks.cuny.edu/gc_etds/4096 Discover additional works at: https://academicworks.cuny.edu This work is made publicly available by the City University of New York (CUNY). Contact: [email protected] INFORMATION TO USERS This reproduction was made from a copy of a document sent to us for microfilming. While the most advanced technology has been used to photograph and reproduce this document, the quality of the reproduction is heavily dependent upon the quality of the material submitted. The following explanation of techniques is provided to help clarify markings or notations which may appear on this reproduction. 1.The sign or “target” for pages apparently lacking from the document photographed is “Missing Page(s)”. I f it was possible to obtain the missing page(s) or section, they are spliced into the film along with adjacent pages. This may have necessitated cutting through an image and duplicating adjacent pages to assure complete continuity. 2. When an image on the film is obliterated with a round black mark, it is an indication of either blurred copy because of movement during exposure, duplicate copy, or copyrighted materials that should not have been filmed. For blurred pages, a good image o f the page can be found in the adjacent frame.
    [Show full text]