DOCSLIB.ORG

7 Dimensioning Section 7.1 Basic Dimensioning Principles Section 7.2 Dimensioning Techniques

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
7 Dimensioning Section 7.1 Basic Dimensioning Principles Section 7.2 Dimensioning Techniques 7 Dimensioning Section 7.1 Basic Dimensioning Principles Section 7.2 Dimensioning Techniques Chapter Objectives • Add measurements, notes, and symbols to a technical drawing. • Apply ASME and ISO standards to dimen- sions and notes. • Differentiate between size dimen- sions and location dimensions. • Specify geometric tol- erances using symbols and notes. • Add dimensions to a drawing using board- drafting techniques. • Use a CAD system to add dimensions, notes, and geometric tolerances to a techni- cal drawing. Playing with Plastics Jonathan Ive says that engineers and designers can now do things with plastic that were previously impossible. What are the characteristics of plastic that give it this ability? 214 Drafting Career Jonathan Ive, Engineer What comes to mind when you think of a mobile phone that offers all these features: multimedia player, access to the Internet, camera, text messaging, and visual voicemail? Probably the iPhone designed by Jonathan Ive, senior vice president of industrial design at Apple Inc., and his product design team. Ive, recipient of many awards, is especially proud of what the iPod shuffl e represents. Originally shipped for $79, its aluminum body clips together with a tolerance of ±0.03 mm—remarkable precision. “I don’t think there’s ever been a product produced in such volume at that price … given so much time and care.… I hope that integrity is obvious.” Academic Skills and Abilities • Math • Science • English • Social Studies • Physics • Mechanical Drawing Career Pathways A bachelor’s degree in engineering is required for almost all entry-level engineering jobs. Some engineers must be licensed by all 50 states and the District of Columbia. Beginning engineers usually work under the supervision of experienced engi- neers. Communication skills are important. Go to glencoe.com for this book’s OLC to learn more about Jonathan Ive. 215 Ashley Troy Photography 7.1 Basic Dimensioning Practices Connect Symbols have a signifi cant function in drafting. Identify three symbols discussed in this section, and explain what they mean? Content Vocabulary • dimensioning • fi nish mark • unidirectional • datums • dimension line • aligned system system Academic Vocabulary Learning these words while you read this section will also help you in your other subjects and tests. • symbols • processes Graphic Organizer Use a table like the one below to organize notes about dimensioning. Basic Dimensioning Go to glencoe.com for this Lines and Symbols for Dimensioning Systems book’s OLC for a downloadable Dimensioning and Types version of this graphic organizer. Academic Standards English Language Arts NCTE National Council of Teachers of English Read a wide range of print and non-print texts to acquire new information (NCTE) NCTM National Council of Teachers of Mathematics Mathematics ADDA American Design Apply appropriate techniques, tools, and formulas to determine measurements (NCTM) Drafting Association ANSI American National Standards Institute Industry Standards ASME American Society of Mechanical Engineers ADDA Section 2 Dimensioning and Tolerancing (ANSI B4.1, ASME Y14.5M) 216 Chapter 7 Dimensioning LOCAL NOTE Lines and Symbols for LEADER O.38 .75 O1.25 Dimensioning 2 HOLES T 1.06 What information does a complete set of R.62 working drawings include? This chapter discusses how to show the size and shape of the objects you draw. It is important to understand the rules and prin- CENTERLINE ciples of size description, or dimensioning. 1.75 USED AS AN EXTENSION Dimensions, or sizes, are measured in either 3.50 LINE O2.12 U.S. customary or metric (SI) units. Decimal EXTENSION LINE divisions and metric units are now most com- monly used throughout the industry and are DIMENSION used exclusively in ASME Y14.5M (the draft- 1.62 ing standard on dimensioning). Notes and symbols that show the type .44 of fi nish, materials, and other information (4.75) needed to make a part are also included in ROUNDS AND dimensioning. A complete set of working REFERENCE DIMENSION FILLETS R.I2 drawings (the drawing or set of drawings from DIMENSION LINE GENERAL NOTE which the part is manufactured) includes Figure 7-1 shape description, measurements, notes, and symbols (see Figure 7-1). Chapter 13 Dimensioning includes measurements, notes, provides more information about working and symbols. drawings. Dimensions on working drawings must be as precise as necessary to allow the man- Standards, and the International Standards ufacturer to create the part or object. When Organization (ISO). dimensions must be precise, they are given in hundredths, thousandths, or ten-thou- Dimension Line sandths of an inch. If the metric system is A dimension line is a thin line that shows being used, the measurements may be in where a measurement begins and where it tenths, hundredths, or even thousandths of ends. It is also used to show the size of angles. a millimeter. The dimension line should have a break in The views on drawings describe the shape it for the dimension numbers. To keep the of an object. To ensure accuracy and effi ciency, numbers from getting crowded, dimension the drafter adds size information to the draw- lines should be at least .38″ (10 mm) from the ing using a system of lines, symbols, and lines of the drawing and at least .25″ (6 mm) numerical values. from each other. In general, a dimension line Lines and symbols are used on drawings to should be placed outside the view outlines. show where the dimensions apply, as shown in Figure 7-2. Professional and trade asso- Extension Line ciations, engineering societies, and certain An extension line is a thin line that extends industries have agreed on the symbols, so the lines or edges of views. It is used to locate people who use the drawings can recognize center points and to provide space for dimen- their meaning. The latest standards informa- sion lines. Because an extension line is not tion on drawings and symbols can be found part of the views, it should not touch the out- in publications from the American Society of line. Start the extension line about .03″ to .06″ Mechanical Engineers (ASME), the Society (1 to 1.5 mm) from the part, and extend it of Automotive Engineers (SAE), the Military about .12″ (3 mm) beyond the last dimension Section 7.1 Basic Dimensioning Practices 217 .38" (I0 mm) MINIMUM FROM LEADER VISIBLE LINE TO DIMENSION LINE 2X R.25 O..75 .25" (6 mm) MINIMUM BETWEEN DIMENSION LINES 2.25 R.88 Figure 7-2 SPACE 1.12 Dimensioning consists of lines, symbols, and placement techniques. 1.88I.88 3.50 SPACE 6.50 .75 EXTENSION LINE .12" (3 mm) R.12 R.25 FINISH MARK 1.25 DIMENSION LINE .62 .50 line as in Figure 7-2. Avoid drawing exten- Some industries use other means to point sion lines that cross each other or that cross out the endpoint of a dimension line or leader. dimension lines. Figure 7-3C shows some examples. These symbols do the same job as arrowheads. For Arrowhead example, slash marks are often used instead of An arrowhead is placed at each end of dimen- arrowheads in architectural drafting. For most sion lines to show where a dimension begins mechanical working drawings, however, the and ends. It is also used at the end of a leader arrowheads shown in Figure 7-3A and B are to show where a note or dimension applies to a preferred. Also, when space is limited, a dot drawing. Refer again to Figure 7-1. may be used to replace arrowheads as shown Arrowheads can be open or solid. Their in Figure 7-3D. shapes are shown enlarged in Figure 7-3A and in actual size in Figure 7-3B. In any The Finish Mark one drawing, they should all be the same size To dimension a drawing correctly, drafters and shape. In a small space, you may need to must know the correct symbols to include on make the arrowheads slightly smaller. drawings as well as the principles of dimen- sioning. Sometimes the symbols indicate which processes are needed. The fi nish mark, or surface-texture sym- THIS bol, shows that a surface is to be machined, 1 UNIT or fi nished. See Figure 7-4 for the standard 2-1 UNITS 2 fi nish mark now in general use, as well as two NOT THIS older forms of the symbol. The point of the fi nish mark symbol should AB touch the edge view of the surface to be fi n- .24 ished or an adjacent extension line. Also, it should be positioned to read from the bottom .30 of the sheet or from the right side of the sheet CD (see Figure 7-4). Leaders Figure 7-3 A leader is a thin line drawn from a note or Arrowheads dimension to the place where it applies (see Figure 7-5). Always place leaders at an angle 218 Chapter 7 Dimensioning 60° Dimensioning Systems .19 (5 mm) and Types .09 (2 mm) What are the two basic types of APPLICATION STANDARD FORM dimensions? 60° Various systems or types of dimensioning .12 (3 mm) 60° can be used and are discussed here. .19 (5 mm) OLD FORM Units OLD FORM When you use the U.S. Customary sys- tem, give the measurements in inches and Figure 7-4 decimals of an inch. When customary dimen- ″ The fi nish mark tells which surfaces are to be sions are in inches, omit the inch symbol ( ). machined. Add a note to the drawing: UNLESS OTHER- WISE SPECIFIED, ALL DIMENSIONS ARE IN INCHES. Sometimes, parts must fi t together with .12 (3 mm) extreme accuracy. In that case, the machinist Ø1.00 must work within specifi ed limits. If the mea- 60° surements are customary, the decimal inch is used.
Load more

Recommended publications
  • 527 White Rose Lane Renovation
    6 5 4 3 2 1 STANDARD ABBREVIATIONS SYMBOLOGY LEGEND 527 WHITE ROSE LANE RENOVATION & AND MTL METAL 1 @ AT FCU FAN COIL UNIT ADDM ADDENDUM FD FLOOR DRAIN NA NOT APPLICABLE 1 2 A7 -01 3 ELEVATION REFERENCE ADJ ADJUSTABLE FDN FOUNDATION NIC NOT IN CONTRACT A2 -01 AFF ABOVE FINISHED FLOOR FE FIRE EXTINGUISHER NO NUMBER AGG AGGREGATE FEC FIRE EXTINGUISHER CABINET NOM NOMINAL 4 2060 Craigshire Road BUILDING CODE INFORMATION GENERAL NOTES AHU AIR HANDLING UNIT FEP FINISH END PANEL NTS NOT TO SCALE EXTERIOR INTERIOR Saint Louis, MO 63146 ALT ALTERNATE FF&E FURNITURE, FIXTURE & EQUIPMENT T. 314.241.8188 PROJECT SUMMARY: 1. THE CONSTRUCTION DOCUMENTS HAVE BEEN CAREFULLY PREPARED BUT MAY NOT DEPICT ALUM ALUMINUM FFE FINISH FLOOR ELEVATION OC ON CENTER SIM F. 314.241.0125 PROJECT INCLUDES THE RENOVATION OF AN EXISTING SINGLE FAMILY EVERY CONDITION TO BE ENCOUNTERED. IT IS THEREFORE THE GENERAL CONTRACTOR & APPROX APPROXIMATE(LY) FG FIBERGLASS OD OUTSIDE DIAMETER ______1 BUILDING SECTION REFERENCE D RESIDENTIAL DWELLING, NEW CONSTRUCTION OF A TWO CAR GARAGE SUBCONTRACTORS RESPONSIBILITY TO FIELD VERIFY ALL CONDITIONS OF THE AFFECTED ARCH ARCHITECT FHCSK FLAT HEAD COUNTERSUNK OFF OFFICE A101 www.kai-db.com TO THE REAR OF THE EXISTING STRUCTURE, AND A COVERED WORK PRIOR TO SUBMITTING A BID. IF CONDITIONS DIFFER OR ADDITIONAL WORK IS REQUIRED ASPH ASPHALT FIN FINISH OH OPPOSITE HAND Missouri State Certificate of Authority #1234567 CONDITIONED CORRIDOR TO CONNECT THE TWO. BEYOND THAT STATED IN THE CONSTRUCTION DOCUMENTS IT IS THE CONTRACTORS AUTO AUTOMATIC FIXT FIXTURE OPNG OPENING SIM RESPONSIBILITY TO BRING SUCH MATTERS TO THE ATTENTION OF THE ARCHITECT IN A WALL SECTION REFERENCE APPLICABLE ST.
    [Show full text]
  • Technical Specifications Part 1 Civil, Structural And
    Civil, Structural & Architectural Specifications ANNEX VIII TECHNICAL SPECIFICATIONS PART 1 CIVIL, STRUCTURAL AND ARCHITECTURAL Page 1 of 234 Civil, Structural & Architectural Specifications ANNEX VIII TABLE OF CONTENTS CHAPTER CHAPTER ONE - SITE PREPARATION & DEMOLITION General Building Demolition CHAPTER THREE - CONCRETE WORKS Cast In Place Concrete Concrete Topping (Decorative Stamped Concrete) CHAPTER FOUR - MASONRY Unit Masonry Exterior Stonework CHAPTER FIVE - METAL WORK Metal Fabrications Round Handrail Diameter 40 mm Plexi Shed CHAPTER SIX - WOODWORK Joinery CHAPTER SEVEN - THERMAL AND MOISTURE PROTECTION Sheet Waterproofing Membrane Roofing Tiles Roofing Metal Roofing Roof Drainage Roof Accessories Flashing And Sheet Metal Joint Sealers (Expansion Joint) CHAPTER EIGHT - DOORS AND WINDOWS Metal Door Frames Wood Doors Aluminum Doors And Windows Glass & Glazing Door Hardware (Ironmongery) CHAPTER NINE - FINISHES Lath And Plaster Floor and Wall Cladding Suspended Ceilings Non-Structural Metal Framing Gypsum Board Interior Stonework Painting CHAPTER TEN - SPECIALTIES Toilet Accessories Epoxy Resin Work Anti-Shatter Window Film Access Control CHAPTER ELEVEN - DRINKING WATER Page 2 of 234 Civil, Structural & Architectural Specifications ANNEX VIII Lebanese Standard Page 3 of 234 Civil, Structural & Architectural Specifications ANNEX VIII CHAPTER ONE SITE PREPARATION & DEMOLITION Page 4 of 234 Civil, Structural & Architectural Specifications ANNEX VIII CHAPTER ONE SITE PREPARATION & DEMOLITION PART 1 - GENERAL SCOPE OF WORK The work comprises of the rehabilitation of the Building. SITE PROTECTION The contractor should take all measures to protect the site and to protect the users during the rehabilitation period as per the Engineer instructions. The contractor should not allow or add any load to the existing body to avoid any risk in construction works.
    [Show full text]
  • Geometry Course Outline
    GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid
    [Show full text]
  • Dimension Guide
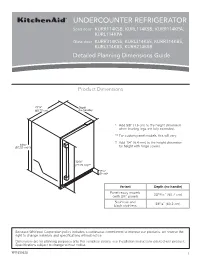
    UNDERCOUNTER REFRIGERATOR Solid door KURR114KSB, KURL114KSB, KURR114KPA, KURL114KPA Glass door KURR314KSS, KURL314KSS, KURR314KBS, KURL314KBS, KURR214KSB Detailed Planning Dimensions Guide Product Dimensions 237/8” Depth (60.72 cm) (no handle) * Add 5/8” (1.6 cm) to the height dimension when leveling legs are fully extended. ** For custom panel models, this will vary. † Add 1/4” (6.4 mm) to the height dimension 343/8” (87.32 cm)*† for height with hinge covers. 305/8” (77.75 cm)** 39/16” (9 cm)* Variant Depth (no handle) Panel ready models 2313/16” (60.7 cm) (with 3/4” panel) Stainless and 235/8” (60.2 cm) black stainless Because Whirlpool Corporation policy includes a continuous commitment to improve our products, we reserve the right to change materials and specifications without notice. Dimensions are for planning purposes only. For complete details, see Installation Instructions packed with product. Specifications subject to change without notice. W11530525 1 Panel ready models Stainless and black Dimension Description (with 3/4” panel) stainless models A Width of door 233/4” (60.3 cm) 233/4” (60.3 cm) B Width of the grille 2313/16” (60.5 cm) 2313/16” (60.5 cm) C Height to top of handle ** 311/8” (78.85 cm) Width from side of refrigerator to 1 D handle – door open 90° ** 2 /3” (5.95 cm) E Depth without door 2111/16” (55.1 cm) 2111/16” (55.1 cm) F Depth with door 2313/16” (60.7 cm) 235/8” (60.2 cm) 7 G Depth with handle ** 26 /16” (67.15 cm) H Depth with door open 90° 4715/16” (121.8 cm) 4715/16” (121.8 cm) **For custom panel models, this will vary.
    [Show full text]
  • Spectral Dimensions and Dimension Spectra of Quantum Spacetimes
    PHYSICAL REVIEW D 102, 086003 (2020) Spectral dimensions and dimension spectra of quantum spacetimes † Michał Eckstein 1,2,* and Tomasz Trześniewski 3,2, 1Institute of Theoretical Physics and Astrophysics, National Quantum Information Centre, Faculty of Mathematics, Physics and Informatics, University of Gdańsk, ulica Wita Stwosza 57, 80-308 Gdańsk, Poland 2Copernicus Center for Interdisciplinary Studies, ulica Szczepańska 1/5, 31-011 Kraków, Poland 3Institute of Theoretical Physics, Jagiellonian University, ulica S. Łojasiewicza 11, 30-348 Kraków, Poland (Received 11 June 2020; accepted 3 September 2020; published 5 October 2020) Different approaches to quantum gravity generally predict that the dimension of spacetime at the fundamental level is not 4. The principal tool to measure how the dimension changes between the IR and UV scales of the theory is the spectral dimension. On the other hand, the noncommutative-geometric perspective suggests that quantum spacetimes ought to be characterized by a discrete complex set—the dimension spectrum. We show that these two notions complement each other and the dimension spectrum is very useful in unraveling the UV behavior of the spectral dimension. We perform an extended analysis highlighting the trouble spots and illustrate the general results with two concrete examples: the quantum sphere and the κ-Minkowski spacetime, for a few different Laplacians. In particular, we find that the spectral dimensions of the former exhibit log-periodic oscillations, the amplitude of which decays rapidly as the deformation parameter tends to the classical value. In contrast, no such oscillations occur for either of the three considered Laplacians on the κ-Minkowski spacetime. DOI: 10.1103/PhysRevD.102.086003 I.
    [Show full text]
  • Zero-Dimensional Symmetry
    Snapshots of modern mathematics № 3/2015 from Oberwolfach Zero-dimensional symmetry George Willis This snapshot is about zero-dimensional symmetry. Thanks to recent discoveries we now understand such symmetry better than previously imagined possible. While still far from complete, a picture of zero-dimen- sional symmetry is beginning to emerge. 1 An introduction to symmetry: spinning globes and infinite wallpapers Let’s begin with an example. Think of a sphere, for example a globe’s surface. Every point on it is specified by two parameters, longitude and latitude. This makes the sphere a two-dimensional surface. You can rotate the globe along an axis through the center; the object you obtain after the rotation still looks like the original globe (although now maybe New York is where the Mount Everest used to be), meaning that the sphere has rotational symmetry. Each rotation is prescribed by the latitude and longitude where the axis cuts the southern hemisphere, and by an angle through which it rotates the sphere. 1 These three parameters specify all rotations of the sphere, which thus has three-dimensional rotational symmetry. In general, a symmetry may be viewed as being a transformation (such as a rotation) that leaves an object looking unchanged. When one transformation is followed by a second, the result is a third transformation that is called the product of the other two. The collection of symmetries and their product 1 Note that we include the rotation through the angle 0, that is, the case where the globe actually does not rotate at all. 1 operation forms an algebraic structure called a group 2 .
    [Show full text]
  • The Datum Reference Frame1 Application of Datums Datums and Datum Reference Frames Are Considered to Be Absolutely Perfect, Which Makes Them Imaginary
    856 SALT LAKE COURT SAN JOSE, CA 95133 (408) 251–5329 The Datum Reference Frame1 Application of Datums Datums and datum reference frames are considered to be absolutely perfect, which makes them imaginary. Measurements cannot be made from theoretical surfaces. Therefore, datums are assumed to exist in and be simulated by processing equipment such as surface plates, gages, machine tables and vises. Processing equipment is not perfect, but is made sufficiently accurately to simulate datums. The three mutually perpendicular planes of a datum reference frame provide origin and direction for measurements from simulated datums to features. Immobilization of a Part Figure 4-1 The three mutually perpendicular intersecting datum planes of a simulated datum reference frame. 1Cogorno, Gene R., Geometric Dimensioning and Tolerancing for Mechanical Design, Second Edition, McGraw-Hill, New York, 2011, p. 50. Technical Training Consultants (408) 251-5329 http://www.ttc-cogorno.com Parts are thought to have six degrees of freedom, three degrees of translational freedom and three degrees of rotational freedom. A part can move back and forth in the X direction, in and out in the Y direction, and up and down in the Z direction, and rotate around the X-axis, around the Y-axis, and around the Z-axis as shown in Figure 4-1. A part is oriented and immobilized relative to the three mutually perpendicular intersecting datum planes of the datum reference frame in a selected order of precedence as shown in Figure 4-2. In order to properly place an imperfect, rectangular part in a simulated datum reference frame, the primary datum feature sits flat on one of the planes with a minimum of three points of contact that are not in a straight line.
    [Show full text]
  • Creating a Revolve
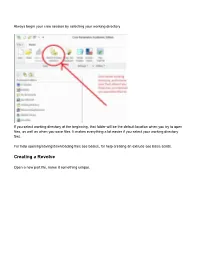
    Always begin your creo session by selecting your working directory If you select working directory at the beginning, that folder will be the default location when you try to open files, as well as when you save files. It makes everything a lot easier if you select your working directory first. For help opening/saving/downloading files see basics, for help creating an extrude see basic solids. Creating a Revolve Open a new part file, name it something unique. Choose a plane to sketch on Go to sketch view (if you don’t know where that is see Basic Solids) Move your cursor so the centerline snaps to the horizontal line as shown above You may now begin your sketch I have just sketched a random shape Sketch Tips: ● Your shape MUST be closed ● If you didn’t put a centerline in, you will get radial instead of diameter dimensions (in general this is bad) ● Remember this is being revolved so you are only sketching the profile on one side of the center line. If you need to put in diameter dimensions: Click normal, click the line or point you want the dimension for, click the centerline, and click the same line/point that you clicked the first time AGAIN, and then middle mouse button where you want the dimension to be placed. After your sketch is done, click the checkmark to get out of sketch, then click the checkmark again to complete the revolve The part in the sketch will look like this: .
    [Show full text]
  • Why Observable Space Is Three Dimensional
    Adv. Studies Theor. Phys., Vol. 8, 2014, no. 17, 689 – 700 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/astp.2014.4675 Why Observable Space Is Solely Three Dimensional Mario Rabinowitz Armor Research, 715 Lakemead Way Redwood City, CA 94062-3922, USA Copyright © 2014 Mario Rabinowitz. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Abstract Quantum (and classical) binding energy considerations in n-dimensional space indicate that atoms (and planets) can only exist in three-dimensional space. This is why observable space is solely 3-dimensional. Both a novel Virial theorem analysis, and detailed classical and quantum energy calculations for 3-space circular and elliptical orbits indicate that they have no orbital binding energy in greater than 3-space. The same energy equation also excludes the possibility of atom-like bodies in strictly 1 and 2-dimensions. A prediction is made that in the search for deviations from r2 of the gravitational force at sub-millimeter distances such a deviation must occur at < ~ 1010m (or < ~1012 m considering muoniom), since atoms would disintegrate if the curled up dimensions of string theory were larger than this. Callender asserts that the often-repeated claim in previous work that stable orbits are possible in only three dimensions is not even remotely established. The binding energy analysis herein avoids the pitfalls that Callender points out, as it circumvents stability issues. An uncanny quantum surprise is present in very high dimensions.
    [Show full text]
  • Fundamental Good Practice Guide in the Design and Interpretation of Engineering Drawings for Measurement Processes
    GPG 79 & 80 6/12/05 9:29 am Page 1 A NATIONAL MEASUREMENT GOOD PRACTICE GUIDE No. 79 Fundamental Good Practice in the Design and Interpretation of Engineering Drawings for Measurement Processes GPG 79 & 80 6/12/05 9:29 am Page 2 The DTI drives our ambition of ‘prosperity for all’ by working to create the best environment for business success in the UK. We help people and companies become more productive by promoting enterprise, innovation and creativity. We champion UK business at home and abroad. We invest heavily in world-class science and technology. We protect the rights of working people and consumers. And we stand up for fair and open markets in the UK, Europe and the world. This Guide was developed by the National Physical Laboratory on behalf of the NMS. Measurement Good Practice Guide No. 79 Fundamental Good Practice in the Design and Interpretation of Engineering Drawings for Measurement Processes David Flack Engineering Measurement Team Engineering and Process Control Division Keith Bevan Bevan Training and Assessment Services Limited ABSTRACT This good practice guide is written for engineers, designers and metrology technicians who wish to understand the basics of the interpretation of engineering drawings in relation to the measurement process. After reading this guide designers should have a better understanding of the measurement process and metrology technicians should be in a better position to interpret the aims of the designer. © Crown Copyright 2005 Reproduced with the permission of the Controller of HMSO and Queen's Printer for Scotland July 2005 ISSN 1368-6550 National Physical Laboratory Hampton Road, Teddington, Middlesex, TW11 0LW Acknowledgements This document has been produced for the Department of Trade and Industry’s National Measurement System Policy Unit under contract number GBBK/C/08/17.
    [Show full text]
  • Dimension Theory: Road to the Forth Dimension and Beyond
    Dimension Theory: Road to the Fourth Dimension and Beyond 0-dimension “Behold yon miserable creature. That Point is a Being like ourselves, but confined to the non-dimensional Gulf. He is himself his own World, his own Universe; of any other than himself he can form no conception; he knows not Length, nor Breadth, nor Height, for he has had no experience of them; he has no cognizance even of the number Two; nor has he a thought of Plurality, for he is himself his One and All, being really Nothing. Yet mark his perfect self-contentment, and hence learn this lesson, that to be self-contented is to be vile and ignorant, and that to aspire is better than to be blindly and impotently happy.” ― Edwin A. Abbott, Flatland: A Romance of Many Dimensions 0-dimension Space of zero dimensions: A space that has no length, breadth or thickness (no length, height or width). There are zero degrees of freedom. The only “thing” is a point. = ∅ 0-dimension 1-dimension Space of one dimension: A space that has length but no breadth or thickness A straight or curved line. Drag a multitude of zero dimensional points in new (perpendicular) direction Make a “line” of points 1-dimension One degree of freedom: Can only move right/left (forwards/backwards) { }, any point on the number line can be described by one number 1-dimension How to visualize living in 1-dimension Stuck on an endless one-lane one-way road Inhabitants: points and line segments (intervals) Live forever between your front and back neighbor.
    [Show full text]
  • DIMENSION* 0.10% Plus Fertilizer NOT for USE on Turf Being Grown for Sale Or Other Commercial Use As Sod, Or for Commercial Seed Production, Or for Research Purposes
    DIMENSION* 0.10% Plus Fertilizer NOT FOR USE on turf being grown for sale or other commercial use as sod, or for commercial seed production, or for research purposes. In New York State this product may only be used by commercial applicators and Warm-Season Grasses at no more than 500 lb (0.5 lb of active ingredient) per acre per year (or 11.5 lb Common Name Scientific Name product per 1,000 ft sq per year) and is prohibited from use in Nassau and Bahiagrass Paspalum notatum Suffolk Counties. Bermudagrass Cynodon dactylon Contains LESCO® Poly Plus® Sulfur Coated Urea to provide a uniform growth Buffalograss*** Buchloe dactyloides with extended nitrogen feeding. Carpetgrass Axonopus affinis ACTIVE INGREDIENT: Centipedegrass Eremochloa ophiuroides Dithiopyr, 3,5-pyridinedicarbothioic acid, 2-(difluoromethyl)-4-(2-methylpropyl)- Kikuyugrass Pennisetum clandestinum 6-(trifluoromethyl)-S,S-dimethyl ester....................................................... 0.10% St. Augustinegrass Stenotaphrum secundatum INERT INGREDIENTS:...................................................................................... 99.90% Zoysiagrass Zoysia, japonica Total: ............................................................................................................... 100.00% DO NOT apply this product to Colonial Bentgrass (Agrostis tenuis) varieties. Product protected by U.S. Patent No. 4,692,184. Other patents pending. *Use of this product on certain varieties of Creeping Bentgrass, such as 'Cohansey', 'Carmen', Read the entire label before using this product. Use only according to label instructions. 'Seaside', and 'Washington' may result in undesirable turfgrass injury. Not all varieties of NOTICE: Before using this product, read the Use Precautions, Warranty Statements, Creeping Bentgrass have been tested. Directions for Use, and the Storage and Disposal Instructions. If the Warranty statements **Use of this product on certain varieties of Fine Fescue may result in undesirable turf injury.
    [Show full text]