Lattice QCD: Commercial Vs
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Computer Hardware
Computer Hardware MJ Rutter mjr19@cam Michaelmas 2014 Typeset by FoilTEX c 2014 MJ Rutter Contents History 4 The CPU 10 instructions ....................................... ............................................. 17 pipelines .......................................... ........................................... 18 vectorcomputers.................................... .............................................. 36 performancemeasures . ............................................... 38 Memory 42 DRAM .................................................. .................................... 43 caches............................................. .......................................... 54 Memory Access Patterns in Practice 82 matrixmultiplication. ................................................. 82 matrixtransposition . ................................................107 Memory Management 118 virtualaddressing .................................. ...............................................119 pagingtodisk ....................................... ............................................128 memorysegments ..................................... ............................................137 Compilers & Optimisation 158 optimisation....................................... .............................................159 thepitfallsofF90 ................................... ..............................................183 I/O, Libraries, Disks & Fileservers 196 librariesandkernels . ................................................197 -

Parallel Computer Architecture
Parallel Computer Architecture Introduction to Parallel Computing CIS 410/510 Department of Computer and Information Science Lecture 2 – Parallel Architecture Outline q Parallel architecture types q Instruction-level parallelism q Vector processing q SIMD q Shared memory ❍ Memory organization: UMA, NUMA ❍ Coherency: CC-UMA, CC-NUMA q Interconnection networks q Distributed memory q Clusters q Clusters of SMPs q Heterogeneous clusters of SMPs Introduction to Parallel Computing, University of Oregon, IPCC Lecture 2 – Parallel Architecture 2 Parallel Architecture Types • Uniprocessor • Shared Memory – Scalar processor Multiprocessor (SMP) processor – Shared memory address space – Bus-based memory system memory processor … processor – Vector processor bus processor vector memory memory – Interconnection network – Single Instruction Multiple processor … processor Data (SIMD) network processor … … memory memory Introduction to Parallel Computing, University of Oregon, IPCC Lecture 2 – Parallel Architecture 3 Parallel Architecture Types (2) • Distributed Memory • Cluster of SMPs Multiprocessor – Shared memory addressing – Message passing within SMP node between nodes – Message passing between SMP memory memory nodes … M M processor processor … … P … P P P interconnec2on network network interface interconnec2on network processor processor … P … P P … P memory memory … M M – Massively Parallel Processor (MPP) – Can also be regarded as MPP if • Many, many processors processor number is large Introduction to Parallel Computing, University of Oregon, -
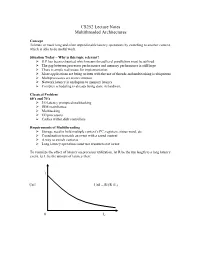
CS252 Lecture Notes Multithreaded Architectures
CS252LectureNotes MultithreadedArchitectures Concept Tolerateormasklongandoftenunpredictablelatencyoperationsbyswitchingtoanothercontext, whichisabletodousefulwork. SituationToday–Whyisthistopicrelevant? ILPhasbeenexhaustedwhichmeansthreadlevelparallelismmustbeutilized ‹ Thegapbetweenprocessorperformanceandmemoryperformanceisstilllarge ‹ Thereisamplereal-estateforimplementation ‹ Moreapplicationsarebeingwrittenwiththeuseofthreadsandmultitaskingisubiquitous ‹ Multiprocessorsaremorecommon ‹ Networklatencyisanalogoustomemorylatency ‹ Complexschedulingisalreadybeingdoneinhardware ClassicalProblem 60’sand70’s ‹ I/Olatencypromptedmultitasking ‹ IBMmainframes ‹ Multitasking ‹ I/Oprocessors ‹ Cacheswithindiskcontrollers RequirementsofMultithreading ‹ Storageneedtoholdmultiplecontext’sPC,registers,statusword,etc. ‹ Coordinationtomatchaneventwithasavedcontext ‹ Awaytoswitchcontexts ‹ Longlatencyoperationsmustuseresourcesnotinuse Tovisualizetheeffectoflatencyonprocessorutilization,letRbetherunlengthtoalonglatency event,letLbetheamountoflatencythen: 1 Util Util=R/(R+L) 0 L 80’s Problemwasrevisitedduetotheadventofgraphicsworkstations XeroxAlto,TIExplorer ‹ Concurrentprocessesareinterleavedtoallowfortheworkstationstobemoreresponsive. ‹ Theseprocessescoulddriveormonitordisplay,input,filesystem,network,user processing ‹ Processswitchwasslowsothesubsystemsweremicroprogrammedtosupportmultiple contexts ScalableMultiprocessor ‹ Dancehall–asharedinterconnectwithmemoryononesideandprocessorsontheother. ‹ Orprocessorsmayhavelocalmemory M M P/M P/M -

Dynamic Adaptation Techniques and Opportunities to Improve HPC Runtimes
Dynamic Adaptation Techniques and Opportunities to Improve HPC Runtimes Mohammad Alaul Haque Monil, Email: [email protected], University of Oregon. Abstract—Exascale, a new era of computing, is knocking at subsystem, later generations of integrated heterogeneous sys- the door. Leaving behind the days of high frequency, single- tems such as NVIDIA’s Tegra Xavier have taken heterogeneity core processors, the new paradigm of multicore/manycore pro- within the same chip to the extreme. Processing units with cessors in complex heterogeneous systems dominates today’s HPC landscape. With the advent of accelerators and special-purpose diverse instruction set architectures (ISAs) are present in nodes processors alongside general processors, the role of high perfor- in supercomputers such as Summit, where IBM Power9 CPUs mance computing (HPC) runtime systems has become crucial are connected to 6 NVIDIA V100 GPUs. Similarly in inte- to support different computing paradigms under one umbrella. grated systems such as NVIDIA Xavier, processing units with On one hand, modern HPC runtime systems have introduced diverse instruction set architectures work together to accelerate a rich set of abstractions for supporting different technologies and hiding details from the HPC application developers. On the kernels belonging to emerging application domains. Moreover, other hand, the underlying runtime layer has been equipped large-scale distributed memory systems with complex network with techniques to efficiently synchronize, communicate, and map structures and modern network interface cards adds to this work to compute resources. Modern runtime layers can also complexity. To efficiently manage these systems, efficient dynamically adapt to achieve better performance and reduce runtime systems are needed. -

R00456--FM Getting up to Speed
GETTING UP TO SPEED THE FUTURE OF SUPERCOMPUTING Susan L. Graham, Marc Snir, and Cynthia A. Patterson, Editors Committee on the Future of Supercomputing Computer Science and Telecommunications Board Division on Engineering and Physical Sciences THE NATIONAL ACADEMIES PRESS Washington, D.C. www.nap.edu THE NATIONAL ACADEMIES PRESS 500 Fifth Street, N.W. Washington, DC 20001 NOTICE: The project that is the subject of this report was approved by the Gov- erning Board of the National Research Council, whose members are drawn from the councils of the National Academy of Sciences, the National Academy of Engi- neering, and the Institute of Medicine. The members of the committee responsible for the report were chosen for their special competences and with regard for ap- propriate balance. Support for this project was provided by the Department of Energy under Spon- sor Award No. DE-AT01-03NA00106. Any opinions, findings, conclusions, or recommendations expressed in this publication are those of the authors and do not necessarily reflect the views of the organizations that provided support for the project. International Standard Book Number 0-309-09502-6 (Book) International Standard Book Number 0-309-54679-6 (PDF) Library of Congress Catalog Card Number 2004118086 Cover designed by Jennifer Bishop. Cover images (clockwise from top right, front to back) 1. Exploding star. Scientific Discovery through Advanced Computing (SciDAC) Center for Supernova Research, U.S. Department of Energy, Office of Science. 2. Hurricane Frances, September 5, 2004, taken by GOES-12 satellite, 1 km visible imagery. U.S. National Oceanographic and Atmospheric Administration. 3. Large-eddy simulation of a Rayleigh-Taylor instability run on the Lawrence Livermore National Laboratory MCR Linux cluster in July 2003. -

Multiprocessors and Multicomputers
Introduction CHAPTER 9 Multiprocessors and Multicomputers Morgan Kaufmann is pleased to present material from a preliminary draft of Readings in Computer Architecture; the material is (c) Copyright 1999 Morgan Kaufmann Publishers. This material may not be used or distributed for any commercial purpose without the express written consent of Morgan Kaufmann Publishers. Please note that this material is a draft of forthcoming publication, and as such neither Morgan Kaufmann nor the authors can be held liable for changes or alterations in the final edition. 9.1 Introduction Most computers today use a single microprocessor as a central processor. Such systems—called uniprocessors—satisfy most users because their processing power has been growing at a com- pound annual rate of about 50%. Nevertheless, some users and applications desire more power. On-line transaction processing (OLTP) systems wish to handle more users, weather forecasters seek more fidelity in tomorrow’s forecast, and virtual reality systems wish to do more accurate visual effects. If one wants to go five times faster, what are the alternatives to waiting four years (1.54 ≈ 5 times)? One approach to going faster is to try to build a faster processor using more gates in parallel and/ or with a more exotic technology. This is the approach used by supercomputers of the 1970s and 1980s. The Cray-1 [31], for example, used an 80 MHz clock in 1976. Microprocessors did not reach this clock rate until the early 1990s. 4/23/03 DRAFT: Readings in Computer Architecture 45 DRAFT: Readings in Computer Architecture Today, however, the exotic processor approach is not economically viable. -

Implementing Operational Intelligence Using In-Memory Computing
Implementing Operational Intelligence Using In-Memory Computing William L. Bain ([email protected]) June 29, 2015 Agenda • What is Operational Intelligence? • Example: Tracking Set-Top Boxes • Using an In-Memory Data Grid (IMDG) for Operational Intelligence • Tracking and analyzing live data • Comparison to Spark • Implementing OI Using Data-Parallel Computing in an IMDG • A Detailed OI Example in Financial Services • Code Samples in Java • Implementing MapReduce on an IMDG • Optimizing MapReduce for OI • Integrating Operational and Business Intelligence © ScaleOut Software, Inc. 2 About ScaleOut Software • Develops and markets In-Memory Data Grids, software middleware for: • Scaling application performance and • Providing operational intelligence using • In-memory data storage and computing • Dr. William Bain, Founder & CEO • Career focused on parallel computing – Bell Labs, Intel, Microsoft • 3 prior start-ups, last acquired by Microsoft and product now ships as Network Load Balancing in Windows Server • Ten years in the market; 400+ customers, 10,000+ servers • Sample customers: ScaleOut Software’s Product Portfolio ® • ScaleOut StateServer (SOSS) ScaleOut StateServer In-Memory Data Grid • In-Memory Data Grid for Windows and Linux Grid Grid Grid Grid • Scales application performance Service Service Service Service • Industry-leading performance and ease of use • ScaleOut ComputeServer™ adds • Operational intelligence for “live” data • Comprehensive management tools • ScaleOut hServer® • Full Hadoop Map/Reduce engine (>40X faster*) -

What Is Parallel Architecture?
PARLab Parallel Boot Camp Introduction to Parallel Computer Architecture 9:30am-12pm John Kubiatowicz Electrical Engineering and Computer Sciences University of California, Berkeley Societal Scale Information Systems •! The world is a large parallel system already –! Microprocessors in everything –! Vast infrastructure behind this Massive Cluster Clusters –! People who say that parallel computing Gigabit Ethernet never took off have not been watching •! So: why are people suddenly so excited about parallelism? –! Because Parallelism is being forced Scalable, Reliable, upon the lowest level Secure Services Databases Information Collection Remote Storage Online Games Commerce … MEMS for Sensor Nets Building & Using 8/19/09 Sensor Nets John Kubiatowicz Parallel Architecture: 2 ManyCore Chips: The future is here •! Intel 80-core multicore chip (Feb 2007) –! 80 simple cores –! Two floating point engines /core –! Mesh-like "network-on-a-chip“ –! 100 million transistors –! 65nm feature size Frequency Voltage Power Bandwidth Performance 3.16 GHz 0.95 V 62W 1.62 Terabits/s 1.01 Teraflops 5.1 GHz 1.2 V 175W 2.61 Terabits/s 1.63 Teraflops 5.7 GHz 1.35 V 265W 2.92 Terabits/s 1.81 Teraflops •! “ManyCore” refers to many processors/chip –! 64? 128? Hard to say exact boundary •! How to program these? –! Use 2 CPUs for video/audio –! Use 1 for word processor, 1 for browser –! 76 for virus checking??? •! Something new is clearly needed here… 8/19/2009 John Kubiatowicz Parallel Architecture: 3 Outline of Today’s Lesson •! Goals: –! Pick up some common terminology/concepts -

Infrastructure Requirements for Future Earth System Models
Infrastructure Requirements for Future Earth System Models Atmosphere, Oceans, and Computational Infrastructure Future of Earth System Modeling Caltech and JPL Center for Climate Sciences Pasadena, CA V. Balaji NOAA/GFDL and Princeton University 18 May 2018 V. Balaji ([email protected]) Future Infrastucture 18 May 2018 1 / 23 Outline V. Balaji ([email protected]) Future Infrastucture 18 May 2018 2 / 23 Moore’s Law and End of Dennard scaling Figure courtesy Moore 2011: Data processing in exascale-class systems. Processor concurrency: Intel Xeon-Phi. Fine-grained thread concurrency: Nvidia GPU. V. Balaji ([email protected]) Future Infrastucture 18 May 2018 3 / 23 The inexorable triumph of commodity computing From The Platform, Hemsoth (2015). V. Balaji ([email protected]) Future Infrastucture 18 May 2018 4 / 23 The "Navier-Stokes Computer" of 1986 “The Navier-Stokes computer (NSC) has been developed for solving problems in fluid mechanics involving complex flow simulations that require more speed and capacity than provided by current and proposed Class VI supercomputers. The machine is a parallel processing supercomputer with several new architectural elements which can be programmed to address a wide range of problems meeting the following criteria: (1) the problem is numerically intensive, and (2) the code makes use of long vectors.” Nosenchuck and Littman (1986) V. Balaji ([email protected]) Future Infrastucture 18 May 2018 5 / 23 The Caltech "Cosmic Cube" (1986) “Caltech is at its best blazing new trails; we are not the best place for programmatic research that dots i’s and crosses t’s”. Geoffrey Fox, pioneer of the Caltech Concurrent Computation Program, in 1986. -

ECE 669 Parallel Computer Architecture
ECE 669 Parallel Computer Architecture Lecture 2 Architectural Perspective ECE669 L2: Architectural Perspective February 3, 2004 Overview ° Increasingly attractive • Economics, technology, architecture, application demand ° Increasingly central and mainstream ° Parallelism exploited at many levels • Instruction-level parallelism • Multiprocessor servers • Large-scale multiprocessors (“MPPs”) ° Focus of this class: multiprocessor level of parallelism ° Same story from memory system perspective • Increase bandwidth, reduce average latency with many local memories ° Spectrum of parallel architectures make sense • Different cost, performance and scalability ECE669 L2: Architectural Perspective February 3, 2004 Review ° Parallel Comp. Architecture driven by familiar technological and economic forces • application/platform cycle, but focused on the most demanding applications Speedup • hardware/software learning curve ° More attractive than ever because ‘best’ building block - the microprocessor - is also the fastest BB. ° History of microprocessor architecture is parallelism • translates area and denisty into performance ° The Future is higher levels of parallelism • Parallel Architecture concepts apply at many levels • Communication also on exponential curve => Quantitative Engineering approach ECE669 L2: Architectural Perspective February 3, 2004 Threads Level Parallelism “on board” Proc Proc Proc Proc MEM ° Micro on a chip makes it natural to connect many to shared memory – dominates server and enterprise market, moving down to desktop -

What Is Parallel Architecture?
PARLab Parallel Boot Camp Introduction to Parallel Computer Architecture 9:30am-12pm John Kubiatowicz Electrical Engineering and Computer Sciences University of California, Berkeley Societal Scale Information Systems • The world is a large parallel system already – Microprocessors in everything – Vast infrastructure behind this Massive Cluster – People who say that parallel computing Gigabit Ethernet Clusters never took off have not been watching • So: why are people suddenly so excited about parallelism? – Because Parallelism is being forced Scalable, Reliable, upon the lowest level Secure Services Databases Information Collection Remote Storage Online Games Commerce … MEMS for Sensor Nets Building & Using 8/15/2012 Sensor Nets John Kubiatowicz Parallel Architecture: 2 ManyCore Chips: The future is here • Intel 80-core multicore chip (Feb 2007) – 80 simple cores – Two FP-engines / core – Mesh-like network – 100 million transistors – 65nm feature size • Intel Single-Chip Cloud Computer (August 2010) – 24 “tiles” with two IA cores per tile – 24-router mesh network with 256 GB/s bisection – 4 integrated DDR3 memory controllers – Hardware support for message-passing • “ManyCore” refers to many processors/chip – 64? 128? Hard to say exact boundary • How to program these? – Use 2 CPUs for video/audio – Use 1 for word processor, 1 for browser – 76 for virus checking??? • Something new is clearly needed here… 8/15/2012 John Kubiatowicz Parallel Architecture: 3 Outline of Today’s Lesson • Goals: – Pick up some common terminology/concepts for later -

The Power of In-Memory Computing: from Supercomputing to Stream Processing
The Power of In-Memory Computing: From Supercomputing to Stream Processing William Bain, Founder & CEO ScaleOut Software, Inc. October 28, 2020 About the Speaker Dr. William Bain, Founder & CEO of ScaleOut Software: • Email: [email protected] • Ph.D. in Electrical Engineering (Rice University, 1978) • Career focused on parallel computing – Bell Labs, Intel, Microsoft ScaleOut Software develops and markets In-Memory Data Grids, software for: • Scaling application performance with in-memory data storage • Providing operational intelligence on live data with in-memory computing • 15+ years in the market; 450+ customers, 12,000+ servers 2 What Is In-Memory Computing? Generally accepted characteristics: • Comprises both hardware & software techniques. • Hosts data sets in primary memory. • Distributes computing across many servers. • Employs data-parallel computations. Why use IMC? • Can quickly process “live,” fast-changing data. • Can analyze large data sets. • “Scaling out” is more scalable and cost- effective than “scaling up”. 3 In the Beginning Caltech Cosmic Cube (1983) • Possibly the earliest in-memory computing system • Created by professors Geoffrey Fox and Charles Seitz • Targeted at solving scientific problems (high energy physics, astrophysics, chemistry, chip simulation) • 64 “nodes” with Intel 8086/8087 processors & 8MB total memory, hypercube interconnect, 3.2 MFLOPS • “One-tenth the power of the Cray 1 but 100X less expensive” 4 The Era of Commercialization Commercial Parallel Supercomputers • 1984: Industry pioneered