Efficient Terrain Triangulation and Modification Algorithms for Game
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Bibliografska I Sadržajna Obrada Video Igara
Sveučilište u Zadru Odjel za informacijske znanosti Diplomski sveučilišni studij Informacijske znanosti - knjižničarstvo Stipe Turčinov Bibliografska i sadržajna obrada video igara Diplomski rad Zadar, 2017. Sveučilište u Zadru Odjel za informacijske znanosti Diplomski sveučilišni studij Informacijske znanosti - knjižničarstvo Bibliografska i sadržajna obrada video igara Diplomski rad Student/ica: Mentor/ica: Stipe Turčinov prof. dr. sc. Mirna Willer Komentor/ica: Dr. sc. Drahomira Cupar, poslijedoktorand Zadar, 2017. Izjava o akademskoj čestitosti Ja, Stipe Turčinov, ovime izjavljujem da je moj diplomski rad pod naslovom Bibliografska i sadržajna obrada video igara rezultat mojega vlastitog rada, da se temelji na mojim istraživanjima te da se oslanja na izvore i radove navedene u bilješkama i popisu literature. Ni jedan dio mojega rada nije napisan na nedopušten način, odnosno nije prepisan iz necitiranih radova i ne krši bilo čija autorska prava. Izjavljujem da ni jedan dio ovoga rada nije iskorišten u kojem drugom radu pri bilo kojoj drugoj visokoškolskoj, znanstvenoj, obrazovnoj ili inoj ustanovi. Sadržaj mojega rada u potpunosti odgovara sadržaju obranjenoga i nakon obrane uređenoga rada. Zadar, 31. listopada 2017. Sadržaj Sažetak ....................................................................................................................................... 1 1. Uvod .................................................................................................................................... 2 2. Deskriptivna i sadržajna -

Dirt 3 Mods Pc Download
Dirt 3 mods pc download LINK TO DOWNLOAD dirt 3 camera mod. Miscellaneous. Uploaded: 13 Nov Last Update: 14 Nov Author: thrive4. Uploader: thrive4. alter camera view in cockpit to roughly 3/4 of steering wheel being visible. MB ; dirt 3 camera mod. Miscellaneous. Uploaded: 13 Nov Last Update: 14 Nov 09/06/ · Dirt 3 está disponível para download via Steam. DiRT 3 conta com ótimos mods para deixar o seu carro mais bonito. Confira como baixar e instalar DiRT 3 no Xbox , PS3, PC e Mac.8/ According to Steam there are currently more active Dirt 3 than Dirt 4 players. There is no special place here for Dirt 3 mods but as Dirt 3 gave many cars, sounds and liveries to it’s younger brother its time that this abandonware receive something back from Dirt Rally. Long live Potato PC racing! Enjoy! - Crystal crisp Dirt Rally quality graphic3,9/5(14). dirt 3 care package. Week 1 of Stay Home. Make Mods. concluded on Sunday 12th April and I want to say a huge thank you to all the authors - old and new - who shared mods with the community through this period. We had a whopping mods from authors across 48 games. DiRT 3 - Any Car Any Track (ACAT) v - Game mod - Download The file Any Car Any Track (ACAT) v is a modification for DiRT 3, a(n) racing renuzap.podarokideal.ruad for free. file type Game mod. file size MB. last update Sunday, April 17, downloads downloads (7 days) Dirt 3 mods are amazing in every way, and it's really good to get them, especially if you want more from the game. -

Download Colin Mcrae Rally 3
Download colin mcrae rally 3 CLICK TO DOWNLOAD 25/10/ · Colin McRae Rally 3 is a racing video game developed and published by Codemasters for Xbox, PlayStation 2 and Microsoft Windows. It is the third game in the Colin McRae Rally series. It features rally cars from the World Rally Championship/5(31). Colin McRae Rally 2, Colin McRae Rally , Colin McRae Rally, Colin McRae Rally 04, Rally Championship , Combat Flight Simulator 3: Battle for Europe, Comanche 4, Daytona USA: Deluxe © San Pedro Software Inc. Contact: done in seconds. Of course the Colin McRae games have always been known for their excellent driving model: this time the game recreates every other aspect of a real rally season as well. We’re left with little choice but to declare Colin McRae Rally 3 the best driving game of E/10(6). Colin McRae Rally 3 is a dirt, racing video game for Microsoft Windows. The Developer are Codemasters, Feral Interactive, Sumo Digital, IOMO, more and Publisher are Codemasters! This Post specially made for computer download, go to footer download link and Download into your PC. Thanks. 04/08/ · Colin McRae Rally 3 v Download. Colin McRae Rally 3; More Colin McRae Rally 3 Fixes. Myth Backup CD Colin McRae Rally 3 v SPA Colin McRae Rally 3 v EURO Colin McRae Rally 3 vA Colin McRae Rally 3 v SPA Add new comment. Your name (Login to post using username, leave blank to post as Anonymous). renuzap.podarokideal.ru's game information and ROM (ISO) download page for Colin McRae Rally 3 (Sony Playstation 2).Operating System: Sony Playstation 2. -

유럽 메이저 퍼블리셔 분석 보고서(5) - Codemasters
유럽 메이저 퍼블리셔 분석 보고서(5) - Codemasters- Codemasters 1. Corporate History 영국 퍼 블리셔/개발사중 2 번째 규모 인 C odemasters 는 1985년 설 립자인 D avid Dar ing이 그 의 형제 와 아 버지 와 함 께 회사를 설 립하였다. 잉글랜드 중부 Wa rwickshire 에 위치 한 C odemasters는 200 5-2006년 회계연도 약 5 천2백만 파 운드 (미화 약 9천3백만 달러)의 매출을 기록 하였다. 20 03-2004년 전 세계 메 이저 TOP 2 0 회사에 포 함되기도 하 였다. 1985-1997 Codemasters는 설립 후 한때 영국 컴퓨터 산업의 견인차 역할을 하였던 ZX Spectrum 컴 퓨터용 퍼즐 액션 게임을 출시하였 다. 이런 종류의 게임에서 가 장 대표적 인 것을 들자면 1986 년에 출시한 Di zzy시리즈다. 이 Dizzy라는 캐릭 터는 후 에 ZX Spectrum 컴퓨 터의 마 스코트로 간 주될 정 도로 게이머 들의 인기를 끌었 다. 이 어 Codemasters는 이 Di zzy 게임 시 리즈를 Commodore 64, Amstrad CPC, Commodore Amiga, Atari ST 같은 컴퓨터를 위한 게임으로도 개발하였다. 자료원: Dizzy Series, Codemasters, 1990 이 Dizzy 시 리즈는 198 6년 ‘Di zzy - The Ultimate Ca rtoon Adventure’편을 시 작으로 1993년 ‘The Excellent Dizzy Collection’까지 총 15개의 시리즈 게임이 출시되었다. 이어 1990년 Cod emasters는 후에 명칭이 Gam e Genie라고 변경된 Power Pak이라는 닌텐도 NES를 위한 게임 장치를 개발하였 다. 1994년 영국 을 중심 을 영연방 국가에서 즐 겨 플레이하고 있는 크 리켓 게임을 소재로 한 게임 을 성 공적으로 출 시하였다. 당 시 웨스 트 인 디아의 전설적인 크 리켓 선수를 브랜 드화하여 2005년까지 4 편의 Brian Lara International Cricket 시리즈 게임 을 출시하였다. 2007년 3 월 시리즈 5번째 게임 인 ‘Bri an Lara Int ernational Cricket 2 007을 Xbo x 36 0, PS2, PC 버전으로 출시 할 예 정이다. -

Colin Mcrae 2005 Windows 7 Fix
Colin mcrae 2005 windows 7 fix You get ERROR when starting the game on new OS? Here is a solution. After installing the game download. By default, the game is incompatible with the OS in version A patch is required to play. 1) Install Colin McRae Rally from the DVD 2). Released on OS X as Colin McRae Rally Mac. OS X release is a universal binary. StarForce DRM has issues on modern versions of Windows. Colin McRae Rally at Wikipedia Colin McRae Rally , kFYatek's Unofficial Windows 7 Patch makes the game compatible with Essential improvements · Video settings · Issues unresolved · Issues fixed. Colin McRae Rally Game Fixes, No-CD Game Fixes, No-CD Patches, its an older game you are playing and you are running Windows 7 or Windows 8 it. Colin McRae Rally v [MULTI5] No-DVD/Fixed Files; Colin McRae If you have problems using a trainer in combination with Windows Vista, 7, 8 or Download Colin McRae Rally Patch v for Win64 now from AusGamers - its free, and no guarantee that this will allow the game to run under Windows 64 bit Edition and WRC 7 FIA World Rally Championship. The following registry settings fixed Colin McRae Rally for me on my Windows 7 64 bit machine. Create a text file and paste the text at the. Codemasters have posted a patch for Colin McRae Rally for those running the Windows 64 bit operating system."This update is provided. Contains the Patch, the official Windows XP x64 Patch and a Crack for Colin McRae Rally The WinXP x64 Patch makes the game compatible with x From what I know, Win7 doesn't have issues with ddraw, so in the best best, seeing how DiRT is a spiritual successor of loved CMR series. -
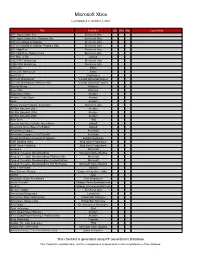
Microsoft Xbox
Microsoft Xbox Last Updated on October 2, 2021 Title Publisher Qty Box Man Comments 007: Agent Under Fire Electronic Arts 007: Agent Under Fire: Platinum Hits Electronic Arts 007: Everything or Nothing Electronic Arts 007: Everything or Nothing: Platinum Hits Electronic Arts 007: NightFire Electronic Arts 007: NightFire: Platinum Hits Electronic Arts 187 Ride or Die Ubisoft 2002 FIFA World Cup Electronic Arts 2006 FIFA World Cup Electronic Arts 25 to Life Eidos 25 to Life: Bonus CD Eidos 4x4 EVO 2 GodGames 50 Cent: Bulletproof Vivendi Universal Games 50 Cent: Bulletproof: Platinum Hits Vivendi Universal Games Advent Rising Majesco Aeon Flux Majesco Aggressive Inline Acclaim Airforce Delta Storm Konami Alias Acclaim Aliens Versus Predator: Extinction Electronic Arts All-Star Baseball 2003 Acclaim All-Star Baseball 2004 Acclaim All-Star Baseball 2005 Acclaim Alter Echo THQ America's Army: Rise of a Soldier: Special Edition Ubisoft America's Army: Rise of a Soldier Ubisoft American Chopper Activision American Chopper 2: Full Throttle Activision American McGee Presents Scrapland Enlight Interactive AMF Bowling 2004 Mud Duck Productions AMF Xtreme Bowling Mud Duck Productions Amped 2 Microsoft Amped: Freestyle Snowboarding Microsoft Game Studios Amped: Freestyle Snowboarding: Platinum Hits Microsoft Amped: Freestyle Snowboarding: Limited Edition Microsoft Amped: Freestyle Snowboarding: Not for Resale Microsoft Game Studios AND 1 Streetball UbiSoft Antz Extreme Racing Empire Interactive / Light... APEX Atari Aquaman: Battle For Atlantis TDK -

GEE Magazin, Kampstr
Die besten Spiele für dein Handy Games To Go Nur 3e Alles über die Killer in Schwarz Konsolenflops Die größten Ninja Gaiden Verlierer der Videospielgeschichte Außerirdisch Der „Space Invaders“-Erfinder im Interview Ninja Gaiden Alles über Der „Space Invaders“-Erfinder im Interview die Killer in Schwarz Außerirdisch Außerirdisch Games To Go Die besten Spiele für dein Handy Die größten Verlierer der Videospielgeschichte Die größten Verlierer Karaoke-Revolution! Konsolenflops Donots, Die Happy, Ferris MC, Elli, Angelika Express: Deutsche Popstars testen Sonys „Singstar“ Die wichtigsten Spiele im Test DTM Race Driver 2, Project Zero 2, Rallisport Challenge 2, Hitman: Contracts, Transformers, Alias, Firefighter F.D. 18, Fight Night 2004, Metroid: Zero Mission 05.2004 05 Donots, Die Happy, Ferris MC, Elli, Angelika Express – Deutsche Popstars testen Sonys „Singstar“ Ferris MC, Elli, Angelika Express Donots, Die Happy, www.geemag.de Februar 2004, Deutschland 3 Euro, Österreich 3,50 Euro, Schweiz 6,90 sfr, 4 196319 703001 sonstiges Ausland 4 Euro Karaoke-Revolution! R © 2004 Pandemic Studios, LLC. All Rights Reserved. Pandemic®, the Pandemic logo® and Full Spectrum Warrior™ are trademarks and/or registered trademarks of Pandemic Studios, LLC and are reproduced under license only. THQ and the THQ logo are trademarks and/or registered trademarks of THQ Inc. All rights reserve ★ Die Trainings-Simulation der US-Army-Infanterie. ★ "Wenn der Spielverlauf nur halb so abwechslungsreich wie die geniale Grafik wird, ist die Xbox um eine Perle reicher." - GamePro 10/2003 "Wenn Full Spectrum Warrior so gut wird, wie es im Moment aussieht, wird Pandemic einige Preise gewinnen." .. - XBM Februar/Marz 2004 "Full Spectrum Warrior hat alle Strategiefans. -

The Localisation of Video Games
The Localisation of Video Games Miguel Ángel Bernal-Merino A thesis submitted in partial fulfilment of the requirements for the degree of PhD Translation Studies Unit Imperial College, London 2013 Copyright Declaration The copyright of this thesis rests with the author, Miguel Ángel Bernal-Merino, and is made available under a Creative Commons Attribution - Non Commercial - No Derivatives licence. Researchers are free to copy, distribute or transmit the thesis on the condition that they attribute it, that they do not use it for commercial purposes and that they do not alter, transform or build upon it. For any reuse or distribution, researchers must make clear to others the licence terms of this work. ii THE LOCALISATION OF VIDEO GAMES TABLE OF CONTENTS ACKNOWLEDGEMENTS vii ABSTRACT viii DECLARATION OF ORIGINALITY Ix LIST OF FIGURES x LIST OF TABLES xii LIST OF GRAPHS xii LIST OF ACRONYMS xiii CHAPTER 1- INTRODUCTION 1 1.1- About video games 4 1.2- About the goals of this research 6 1.3- About the structure of this PhD 7 CHAPTER 2- GAMES, MARKETS AND TRANSLATION 11 2.1- Towards a classification of terms relating to video game products 14 2.1.1- Comprehensive terms 14 2.1.1.1- Game 15 2.1.1.2- Electronic game 18 2.1.1.3- Digital game 19 2.1.1.4- Multimedia interactive entertainment software 19 2.1.1.5- Video game 21 2.1.2- Narrow terms 24 2.1.2.1- Location of play 25 2.1.2.2- Gaming platform 28 2.1.2.3- Mode of distribution 33 2.1.2.4- Type of market 35 2.2- The penetration of video games in today’s world 36 2.2.1- Mainstream games 37 -

Colin Mc Rally 2 Download Full Version
Colin mc rally 2 download full version Download Colin McRae Rally 2 for Windows. Compatible with your OS; Full paid version; In English. Version: Demo; Size: MB; Filename: Colin McRae Rally 2, free and safe download. Colin McRae Rally 2 latest version: Demo of the second version of the classic rally racing game. Colin McRae. Colin McRea Rally 2 features a completely overhauled graphics engine, with advanced imaging techniques like hardware T&L (transform and. Download Colin McRae Rally 2 • Windows Games @ The Iso Zone • The Ultimate Retro Gaming Resource. This second game features the spec Ford Focus WRC, the spec Ford Focus RS WRC, Mitsubishi Lancer EVO VI Gr.A, Subaru. Download 1- 2- 3- 4- 5-http. Colin McRae Rally (PC) [] Free Dowload ▻ Download: Program available in:In English; Program license:Trial version; Program by: Colin McRae Rally 2 is the second game in the Colin McRae racing series helped spawn a full series of more than 10 incredible games for a number of platforms. Colin McRae Rally 2 Free Download PC Game Cracked in Direct Link and Torrent. Colin McRae Rally 2 is a rally simulation game. Colin McRae Rally full game free pc, download, play. -yellowstone-2/ Colin McRae Rally game online, download Colin McRae Rally. Colin McRae Rally , gra wyścigowa wydana w roku przez Codemasters. Gra ukazała się dla komputerów PC oraz konsolę PlayStation. Colin McRae. Colin McRae Rally gives you the option of driving a , pound sports machine as you compete in Rally and Arcade driving competitions. The Rally. Colin McRae Dirt 2 PC Game Free includes five different event types: Rally, Rallycross, "Trailblazer", "Land Rush" and "Raid". -

000 Front Page.Pub
007 Racing * 007: Licence to Kill* 100% Dynamite* 1000 Miglia * 1000cc Turbo * 12 Volt * 18 Wheeler * 18 Wheeler: American Pro Trucker * 18 Wheels of Steel Across America * 18 Wheels of Steel: Convoy * 187 Ride or Die * 19 Part 1: Boot Camp* 1nsane * 1Xtreme * 280 ZZZAP * 3D Deathchase* 3D Real Driving * 3D Scooter Racing * 3D Slot Car Racing * 3D Stock Car Championship* 3D Ultra RC Racers * 3D Waterski * 4 Wheel Thunder * 4D Sports Driving * 4D Sports Driving Master Tracks I * 4-Wheel Thunder * 4x4 EVO 2 * 4X4 Evo 2 * 4x4 EVO 2 * 4x4 Evolution * 4X4 Evolution * 4x4 Evolution * 4X4 Evolution 2 * 4x4 Off-Road Racing* 4x4 Off-Road Racing * 4x4 World Trophy * 4X4 World Trophy * 500cc GP * 500cc Grand Prix * 500cc Motomanager * 5th Gear * 750cc Grand Prix* 911 Tiger Shark * A2 Racer * A2 Racer II * A2 Racer III: Europa Tour * AB Cop * Ace Combat 3 * Ace Combat 3: Electrosphere * Ace Driver * Ace Driver Victory Lap * Action Biker* Action Biker * Action Fighter* Action Girlz Racing * Adrenalin * Adrenalin 2 * Adrenalin 2: Rush Hour * Adrenalin Extreme Show * Advan Racing * Advance GTA * Advance GTA 2 * Advance Rally * Aero Fighters Assault * AeroGauge * African Raiders-01 * African Trail Simulator* Agent X* Air Race * Air Race Championship * Al Unser Jr.'s Turbo Racing * Al Unser Jr's Road to the Top * Al Unser, Jr. Arcade Racing * Alarm for Cobra 11: Hot Pursuit * Alfa Romeo Racing Italiano * All Japan Grand Touring Car Championship * All Points Bulletin * All Terrain Rally * All Terrain Vehicle Simulator * Alley Rally * All-Star Racing * -

18 Wheeler: American Pro Trucker ™ by Acclaim Auto Modellista by Capcom Entertainment Burnout 2: Point of I
PS2 FORCE FEEDBACK TITLES 18 Wheeler: American Pro Trucker ™ by Acclaim Auto Modellista by Capcom Entertainment Burnout 2: Point of Impact™ by Acclaim Burnout 3 Takedown™ by Electronic Arts Burnout™ by Acclaim Burnout™ Revenge by Electronic Arts Colin McRae™ 2005 by Codemasters Colin McRae™ 3 by CodeMasters Software Colin McRae™ Rally 4 by Codemasters Corvette® by Global Star Software Driven by Bam Entertainment Enthusia Professional Racing by Konami F1™ 2001 by Electronic Arts F1™ 2002 by Electronic Arts F1™ Career Challenge by Electronic Arts Ferrari® F355 Challenge™ by Sega Flatout™ by Empire Interactive Flatout™ by Empire Interactive Ford Mustang: The Legend Lives by 2KGames Formula One 2001™ by Sony Computer Entertainment Europe Formula One 2002™ by Sony Computer Entertainment Europe Formula One 2003™ by Sony Computer Entertainment Europe Formula One 2004™ by Sony Computer Entertainment Europe Gran Turismo™ 3 Aspec by Sony Computer Entertainment Inc. Gran Turismo™ 4 by Sony Computer Entertainment Inc. Gran Turismo™ 4 by Sony Computer Entertainment Inc. Gran Turismo™ Concept: 2001 Tokyo by Sony Computer Entertainment Inc. Gran Turismo™ Concept: 2002 TokyoGeneva by Sony Computer Entertainment Inc. Grand Prix Challenge by Atari Hot Wheels ™ Velocity X by THQ Initial D: Special Stage by Sega Juiced™ by THQ Knight Rider™ by Universal Interactive Lotus Challenge™ by Virgin Interactive Entertainment Midnight Club™ 3: DUB Edition by Rockstar Games Midnight Club™ 3: DUB Edition by Rockstar Games Midnight Club™ II By Rockstar Games Motor -

Fiesta RS WRC's Starring Role in Dirt 3 Culminates Ford's History In
NEWS Fiesta RS WRC’s Starring Role in DiRT 3 Culminates Ford’s History in Racing Video Games • The 2011 Ford Fiesta RS WRC, based on Ford’s successful Fiesta road car, is the star of Codemasters’ new rallying game DiRT 3 • More than 40 Fords have starred in more than 20 video games since 1998, with the Focus and Mustang featured most often COLOGNE, Germany, May 23, 2011 – YouTube sensation Ken Block’s fiery Ford Fiesta RS WRC 2011 shreds up rallies in the hotly anticipated new video game DiRT 3 by Codemasters. Veteran gamers know the souped-up Fiesta rally car is only the latest in a long line of fast Fords that have starred in some of most popular racing video games for more than a decade. The tradition officially started in earnest in 1998 when gamers had a chance to drive the Ford Escort WRC 4WD in the first chapter of Codemasters’ racing title, Colin McRae Rally, named after the late WRC star. One year later, the powerful Ford Focus RS WRC graced the cover of the 2.0 version of the game. The car was a virtual version of the vehicle Colin McRae drove in the 1999 WRC championship. For petrol-heads, the virtual racing is a realistic simulation of the high-horsepower thrill of motorsports. For Ford, participating in video games has been a way to reach millions of racing enthusiasts around the world. “Video games have become so realistic you can almost smell the burning rubber,” says Mark Bentley, licensing manager, Ford Global Brand Licensing.